Одна модель общей теории перспективы Б. В. Раушенбаха

ОДНА МОДЕЛЬ ОБЩЕЙ ТЕОРИИ ПЕРСПЕКТИВЫ Б. В. РАУШЕНБАХА

А. В. Бритов, А. Э. Чудаев

В статье описаны три этапа проектирования: проектирование на картинную плоскость, плоскости - на сферу радиуса R, бесконечная картинная плоскость отображается на конечную поверхность сферы и мозг перерабатывает сложное сферическое изображение картинной плоскости так, что некоторые прямые отображаются в прямолинейные отрезки (для всех прямых это невозможно). В результате построения делается вывод, что обратная перспектива возникает начиная с некоторой линии. Определяется уравнение этой линии. Используя программу, разработанную А. Э. Чудаевым, приводятся примеры обратной перспективы, как на основе стандартного (чертежного) изображения £₃ на плоскости, так и на основе изображения в классической перспективе.

В книге Б. В. Раушенбаха изложена так называемая об-и^ая теория ■перспектива, в которой экспериментально обосновывается кроме классической прямой перспективы обратная перспектива, интуитивно отражаемая в работах некоторых художников [1]. Психологически прямая перспектива удаляет изображение, а обратная - включает зрителя и изображаемое пространство. При этом евклидова геометрия пространства очень сильно искажается как в прямой, так и в обратной перспективе- На самом деле многие наблюдения и выводы, приведенные в книге, могут быть оправданны и уточнены идеализированной моделью проектирования пространства на сетчатку глаза, что и было предложено А. В. Бритовым. Идеализация заключается в том, что глаз рассматривается строго сферическим и хрусталик заменяется точкой S - центром проектирования, отбрасываются возможные преломляющие свойства среды внутри глаза. Мы специально вводим картинную плоскость О^Т), на которую предварительно проектируются пространство Охух. Ее удаление h от центра S проектирования в реальной ситуации очень сильно зависит от наличия ближайших достаточно крупных объектов и потому в интерьере к исчисляется несколькими метрами, а на природе может доходить до нескольких километров. В дальнейшем именно к мы берем за единицу масштаба.

На первом этапе проектирование ведется на картинную плоскость (рис. 1).

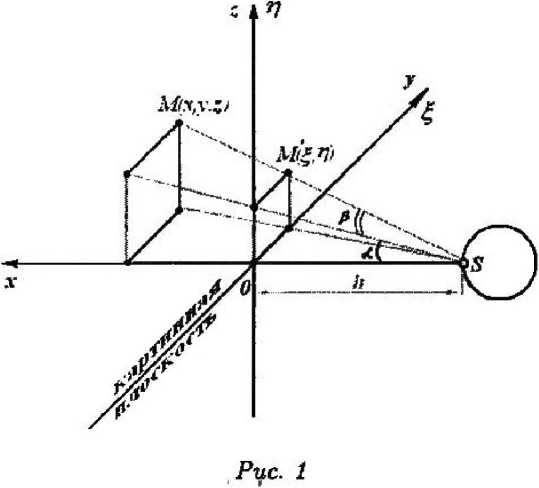
При этом очевидно, что

hy _ hz z 4- h’ ^   $ + /i’

где h. - расстояние от центра проектирования (глаза) до картинной плоскости. На втором этапе рассматривается проектирование картинной плоскости на сферу радиуса R (рис. 2).

: кП

X

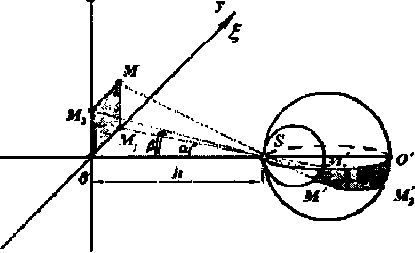
Рис. 2

При этом равные алгебраические отрез* ки МаМ = OMi = 6 и MiM — OMi = л отображаются в неравные М^М* ^ О'М^ М*_гМ' ^О'М^.

(УМ^ — 2R- arctan ™.

га

О'М^ = 2R ■ arctan -,         (2)

М^М' =

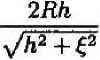
arctan

у/^+ё5

М^М' =    — arctan ,     -

У^+ё V^^n2

«Считыванием координат на сфере требует дополнительных допущегшй. Мы исходим из того, что принимаем за координаты образа

^ — О'Mi — 2 - R - arctan , fir

?7 = О'М2 = 2 • R- arctan 5.

Полагая, как уже отмечалось, h = 1 и определив коэффициент гомотетии произвольно, получаем формулы:

£ = А • arctan ———, $+1

п = А ■ arctan ——, л > — 1, '             т +1

выражающие (£, fj) через (л, у, z) и промежуточные формулы:

£ = А - arctan £, т) = X • arctan ту.

Заметим еще, что (см. рис. 1)

£ = h- tgo, fj^ h- tg£.

Следующий, третий, этап моделирования опирается на следующие факты и гипотезы:

очевидно, что бесконечная по (£, ^картинная плоскость отображается на конечную поверхность сферы (£,77), гДе

• - f А < ^ < f ■ А, — Д ■ А < 77 < Д А;

  - последняя в работе гипотеза заключается в том, что мозг перерабатывает сложное сферическое изображение картинной плоскости (£,77) в (£,77) так, что некоторые прямые отображаются в прямолинейные отрезки (для всех прямых это невозможно). Из формул (4) и (5) видно, что можно сохранить прямолинейность горизонтальных и вертикальных линий, если считать £и 77 прямоугольными координатами точки, и тогда картинная плоскость (£,77) преобразуется в картинный прямоугольник (£,т?).

Пользуясь формулами (4) при А = 1, рассмотрим изображение плоскости (рис. 3) в плоскость (£, ^) (рис. 4) при разных значениях z = zq, т. е. для горизонтальных плоскостей разного уровня. За счет симметрии ограничимся значениями у > 0.

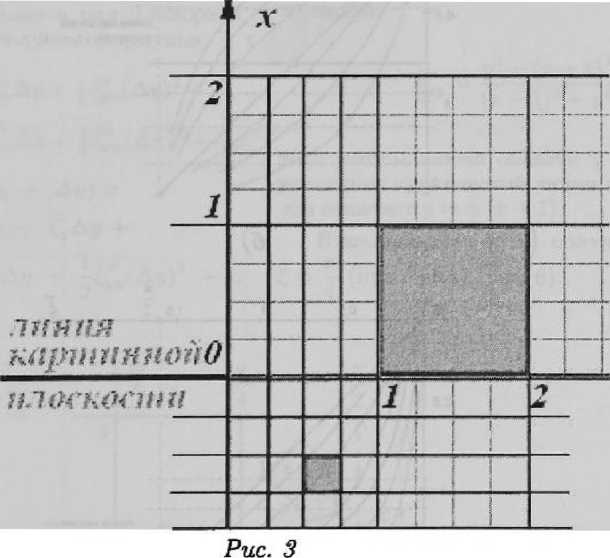
Для построения используем таблицу соответствующих значений. На рис. 4 хороню видно изменение характера изображения при удалении плоскости «вниз».

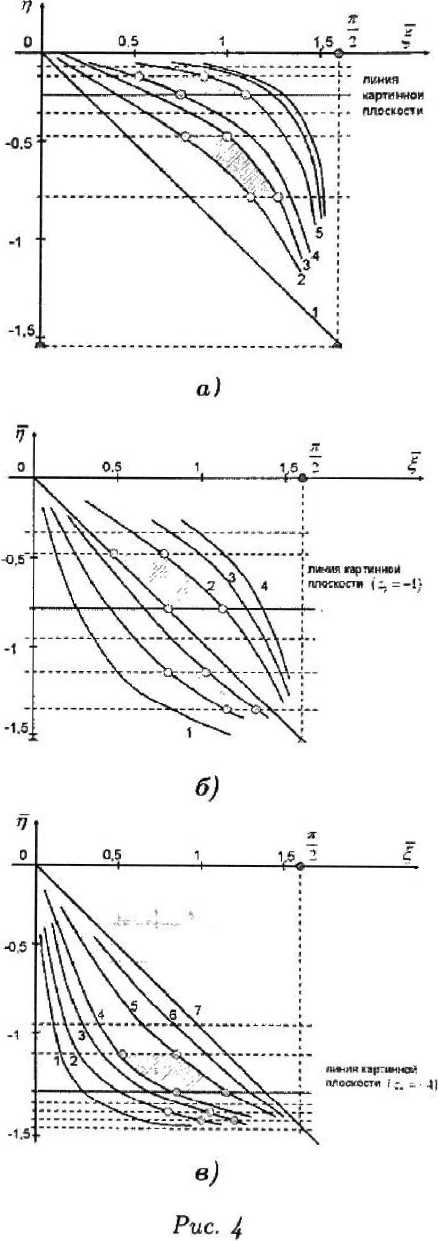
Отметим, что обратная перспектива возникает начиная с некоторой линии у = /($) (или у — <р(б))> Для определения уравнения этой линии (хотя бы приближенно) надо рассмотреть точку Мо(т,у) и просле дить, на каком уровне при бесконечно малом перемещении вдоль координатной линии X = х и У = у, Дт > 0, Ду > О горизонтальные отрезки MqMi « М2М3 (рис. 5).

М^у)

Mv(xsy + Ay)

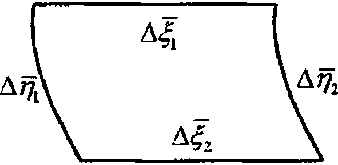
М2(х+ Ах, у)

М^х + Ах у + Ду)

Рис. 5

Заметим, что

△ 61 = б(=₃ у + Ду) - б^у)

△ 6 = б^ + Дт,у + Ду) - 4(х + Дх,у).

Используя разложение в ряд Тейлора и обозначив б — 4(я, у), получим формулы:

^х, у + Ду) = б + б^Ду + |4и_У(Ду)² + -, б(х + д^, у) = 6 + ^Дх + ^_х (АхУ +..., б(ж + Ах,у + Ду) =

= 4 + б^А1 + буАу +

+ ^(А^)2 + С^Ау + 5буУ(Ау)2 + ...

Таким образом,

△41 - Д6 = б^ЛжДу 4- - и так как

:„ _ У² - (Т + I)²

■^ (ж + 1)2 + у2’ то с учетом нашей области у > 0 получим уравнение критической линии в виде бяу = О, что означает у — ± (ж 4-1).

В координатах (б,^?) получим уравнение б = ^ (при А = 1) (рис. 6).

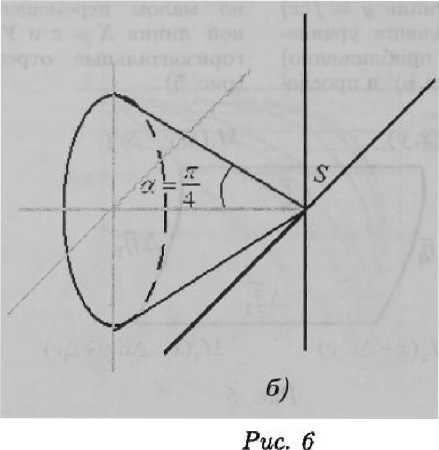
Таким образом, критическая линия, разграничивающая сходящиеся «параллельные» от расходящихся в этой модели имеет уравне-™е « = 4'

Из рис. 2 и формулы (6) следует, что углу зрения а < ^ (^ < f) отвечает прямая перспектива, а значениям а, р > — -обратная. Мы считаем, что это достаточно хорошо отвечает реальным ощущениям.

Приведем примеры обратной перспективы, полученные с помощью программы, разработанной А. Э. Чудаевым.

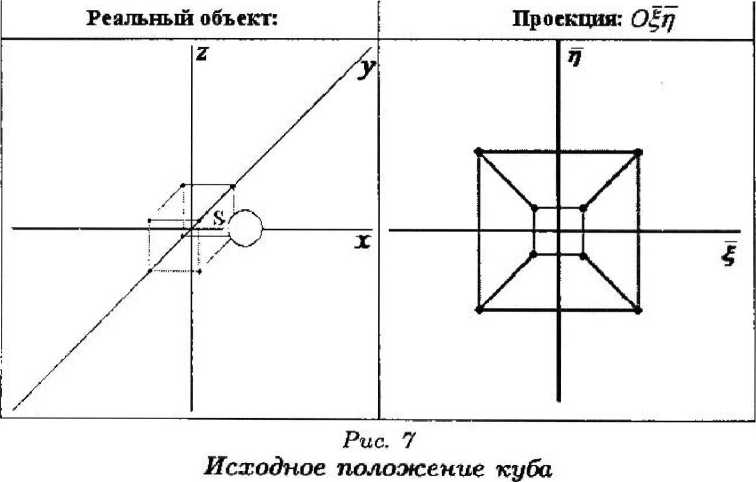
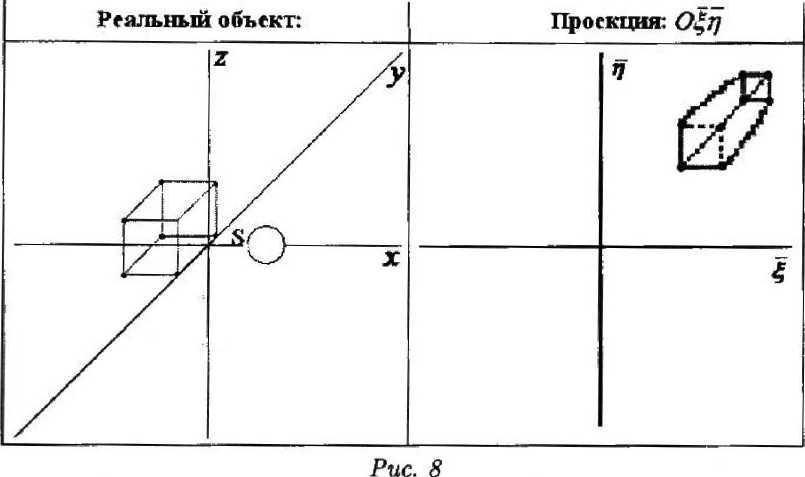
Смещение куба по оси У на 1,4 единиц-ы влево, по оси Z - на 1,4 единицы вверх

Видим обратную перспективу. Аналогично можно рассмотреть случаи, когда куб находится в отрицательной полуплоскости.

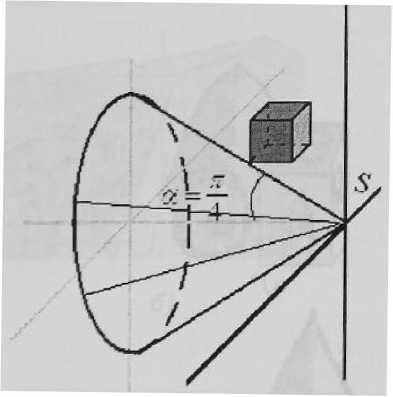
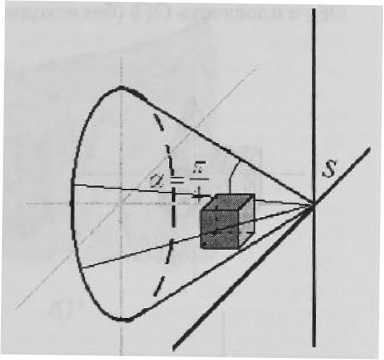
а) зона обратной перспективы.

Рис. 9

б) зона пря-мой перспективы

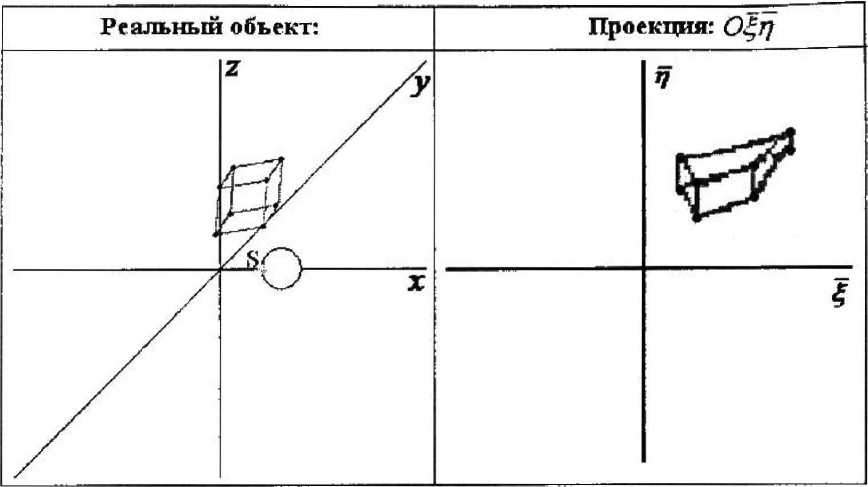
Рис. 10

Сдвиг с вращением в точку начала обратной перспективы (на 1 единицу вправо по оси У, на 1 единицу вверх по оси Z)

Ниже на рис. показано прямое преобразование изображения в картинной плоскости О^т) в плоскость О^ (без исходного простран ства Oxyz\ т. е. с использованием только формул (5).

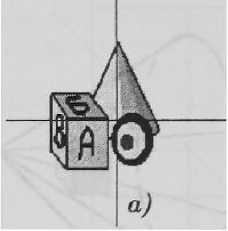
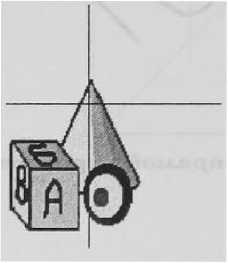
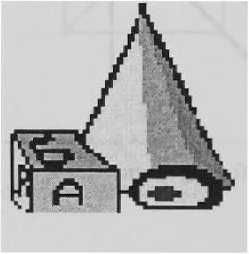
б)’

Рис. 11

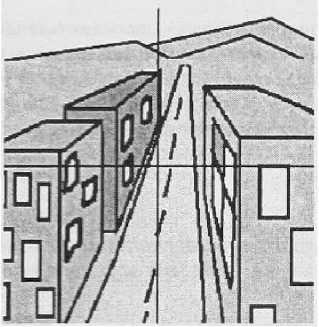
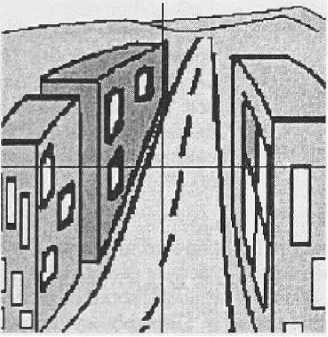
На рис. 12 (а, б) изображена стандартная «картина» (с линейной прямой перспективой при разных смещениях «наблюдателя»), а на рис. 12 (а\ _б’) приводятся изображения в плоскости О^.

Видны характерные особенности:

• -    прямая, близкая к прямолинейной, перспектива наблюдается только па достаточно большом расстоянии от наблюдателя, вблизи она становится криволинейной;

• -    хорошо видны участки обратной перспективы.

  
  
  
  
  
  

  а)

  
  

  а)⁵

  
  
  
  
  
  
  
  

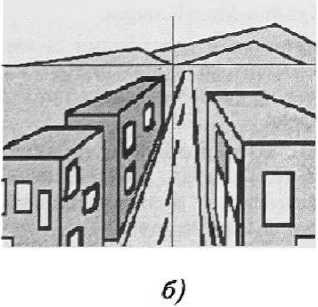
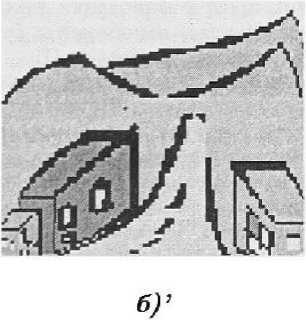
Рис. 12