Односторонние интегральные операторы с однородными ядрами в гранд-пространствах Лебега
Автор: Умархаджиев Салаудин Мусаевич
Журнал: Владикавказский математический журнал @vmj-ru
Статья в выпуске: 3 т.19, 2017 года.
Бесплатный доступ
Получены достаточные и необходимые условия на ядро и грандизатор для ограниченности односторонних интегральных операторов с однородными ядрами в гранд-пространствах Лебега на R+ и Rn, а также получены двусторонние оценки гранд-норм таких операторов. Кроме того, в случае радиального ядра получены двусторонние оценки для норм многомерных операторов в терминах сферических средних и показано, что этот результат сильнее, чем неравенства для норм операторов с нерадиальным ядром.
Односторонний интегральный оператор, оператор с однородными ядрами, гранд-пространство лебега, двусторонние оценки, сферические средние
Короткий адрес: https://sciup.org/14318584
IDR: 14318584 | УДК: 517.982, | DOI: 10.23671/VNC.2017.3.7132
Текст научной статьи Односторонние интегральные операторы с однородными ядрами в гранд-пространствах Лебега
Мы рассматриваем многомерные интегральные операторы
K f (x) := j K (x,y)f (y) dy, K+f (x) := J
K +(x,y)f (y) dy, x G Rn, n > 2,
|y|6|x| |y|>|x| с ядрами K -(x,y) 11 K +(x,y) однородны ми степени —n. а при n = 1 — их версии для полуоси:
x∞
K -f (x) := J
к-(x,y)f (y) dy, K +f (x) := J K +(x,y)f (y) dy, x G R+, в гранд-пространствах Lp)(Rn) и Lp)(R+) соответственно.
Гранд-пространства Лебега Lp) (П), 1 < p < то, по ограничение>му множеству П С Rn ввели Т. Iwaniec и С. Sbordone [6] в связи с приложениями в дифференциальных уравнениях. Операторы гармонического анализа, интенсивно исследовались в таких пространствах и они продолжают привлекать внимание исследователей в связи с различными их приложениями. Некоторые из этих результатов отражены в книгах [8] и [9].
В статьях [3, 11, 12] предложен подход, позволяющий ввести гранд-пространства Лебега Lp)(H), 1 < p < то, на множествах П С Rn не обязательно конечной меры. Этот
подход основан на введении в норму гранд-пространства малой степени неотрицательной функции a(x) (см. (1)). Эту функцию, определяющую гранд-пространство La)(Q), называем грандизатором. Такие гранд-пространства Lp) (Q) и действия в них некоторых операторов гармонического анализа исследовались в работах [2, 4, 5, 15]. Предложенные в этих работах подходы позволили рассматривать в гранд-пространствах такие операторы, как потенциал Рисса, операторы Харди и др. В работе [13] были найдены условия на a(x)
Рисса в гранд-пространствах La)(Rn), и исследовано их взаимодействие с гиперсингулярными интегралами (см. [10] относительно гиперсингулярных интегралов).
Интерес к интегральным операторам с однородными ядрами связан с тем, что класс таких операторов содержит огромное количество разнообразных классических операторов, возникающих в приложениях, например, операторы Харди, оператор Гильберта, весовые потенциалы Рисса, мажоранты коммутантов сингулярных операторов Кальдерона — Зигмунда со степенными весами и многие другие.
a щие ограниченность односторонних интегралных операторов одномерных с однородными ядрами степени — 1 я многомерных с радиальными однородными ядрами степени —n в гранд-пространствах Лебега, а также получены оценки сверху их норм. Основные результаты содержатся в теореме 3.1 в одномерном случае, в теореме 4.4 в случае радиального грандизатора и в теореме 4.5 в случае нерадиального грандизатора.
Обозначения. Rn — n-мерное евклидов о пространство, R+ = (0, то); Sn-1 — единичная сфера в Rn с центром в иатюле координат. |Sn-1| — ее плотладь: S n-1 = {x G Rn : n
|x| = 1}, |Sn-1| = ГП2)- B (xo,r) ~ шар в Rn ращiyca r с центром в точке x0; p = p-д.
где
kf kLP (Q ,w ) =
|f (x)|pw(x)
. Q
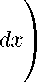
1 p
В случае w = 1 будем писать Lp(Q,w) = Lp(Q).
Следуя работе [3], определяем гранд-пространства Лебега на множествах Q произвольной (не обязательно конечной) меры равенством
W)-
ff
: kf II
pP)(U
) := SUP Е
P
-
Е
kf IL-e foah < ТО| , 1 TO, (1)
La
(Q)
0
где a(x) — произвольная измеримая псотршигтелыпгя функция на. Q. которую мы называем грандизатором. Выбор грандизатора для определения гранд-пространства может диктоваться задачами для исследования таких пространств. В работах [3, 11, 12] предполагалось, что a G L1 (Q), что гарантирует вложение Lp(Q) ^ La)(Q). В данной статье мы имеем дело с Q = R+ ил и Q = Rn и при рассмотрении операторов с однородными ядрами мы находим удобным не обязательно предполагать интегрируемость грандизатора в начале координат и на бесконечности, но всегда предполагаем его локальную интегрируемость вне начала координат:
a(x) G L^BsN) для любых 0 < 5 < N < то, где B§n = {x : 6 < |x| < N}, с заменой слоя B§n на iiiiтервал (5, N) в одномерном случае.
Определенное таким образом гранд-пространство зависит, вообще говоря, от выбора грандизатора, хотя разный выбор грандизаторов может привести к одному и тому же гранд-пространству (см. [14]).
При a Е L1 (И) имеет место цепочка вложений
Lp(Q) ^ Lp)(Q) ^ Lp-e1 (Q,a
p
) ^ Lp-e2(Q,a
p
), 0 < £1<£2
- 1. (2)
ЗАМЕЧАНИЕ 2.1. При обычно используемом определении гранд-пространства Лебега на ограниченных множествах с a(x) = 1 всегда справед
либо
вложение Lp(Q) ^ Lp^Q), т. е. в этом смысле гранд-пространство является расширением классического пространства Лебега. Согласно (2), аналогичное вложение на множествах бесконечной меры гарантируется условием
a Е
L1 (И). Это условие часто предполагается при рассмотрении гранд-пространств на неограниченных множествах (см., например, [3, 13]), хотя гранд-пространства на таких множествах могут рассматриваться и без этого условия.
Пусть a(x) — положительная встоду конечная на полуоси R+ функция. Функцию a(xt) a* (t) = sup
x>
0
a(x)
называют
растяснсением функции a
(см. [1, с. 75]). Отметим следующие свойства растяжений:
(ao) Если фуикция xYa(x). 7
Е
R, не возрастает на R+. то a*(t) 6 tY д.ля
t >
1.
(bo) Если фуиктщя xYa(x). 7
Е
R, не убывает на R+. то a*(t) 6 tY дтя
t <
1.
Пример
2.1. Для функции a(x) = x-A(1 + x)A-Y, А,7 Е R, x Е R+, имеем
a*(t) = t X sup x>0
t
-
max
{λ,γ}
, t
-
min
{λ,γ}
,
0 < t 6 1,
t
> 1.
2.2. Об операторах с однородными ядрами.
Будем рассматривать одномерные операторы
K
в предположении (щиородпости ядра K(x,y) степeiiii —1 11 многомерные операторы
K
в следующих предположепиях на. ядро K(x,y):
(ai) K(x, y) однородно степени —n: (bi) K(x, y) инвариантно относ•ителыю вращений K(w(x),w(y)) = K(x,y). г,те ш — Rn. В книге [7, с. 69] доказано, что интегралы j |K(a,y)||y|-П dy, a Е Sn-1, Rn
У
|K
(
y,0
)
||y| p0 dy, 0
Е
Sn-1,
0
to,
Rn при условиях (a1) 11 (b1) не зав!юят от a Е Sn-1 11 0 Е Sn-1 соответствеппо ii j |K(a,y)| |y|-n dy = j |K(y,0)| |y|-pn0 dy, p0 = p—-у. Rn Rn Легко видеть, что в рассматриваем случае j |K-(a,y)||y|-П dy = j K-(y,0)||y|-p0 dy. Ы>Ы |y|6|x|-1 Мы будем пользоваться обозначениями
^
1
K-
:=
j
1K-(1,y)1
y-p dy, K+
:=
j
1K +(y, 1)1
y
p0
dy, n
= 1.
Для удобства изложения материла статьи в случае радиальных ядер: K (x,y) = k (|x|, |y|), K + (x,y) = k+(|x|, |y|), и в одномерном случае введем две функции
κ
n
(а) :=
1
|k (t, 1)|tn 1
р0 dt,
к
+
(а)
∞ j |k+(t, 1)|tn-1-a dt, 1
α
∈
R
.
Отметим, что
к-
(1) = к и к+(1) =
k
+
.
3. Одномерный случай Обозначим c (a) := sup
0
∞ j |K " (x, 1) | 1 __1 E x (p-E) a* (x)p(p-E) dx,
c
+(
a
) :=
sup
0
j
|
K
+ (x, 1) |
0
__1 E x (p-E)0 a* (x)p(p-E) dx.
Теорема 3.1.
Пусть
1
< p <
то,
функции K
- (x, y)
и K
+ (x,y)
однородны степени
— 1
11 a
— грани
г затор па
R+.
I. Если выполнены условия c-(a) < то и c+(a) < то, то операторы K- и K+ соответственно ограничены в гранд-пространстве Лебега Lp)(R+), при этом kK') 6 c-W, kK +kL?(R+) 6 c+W- <5)
II.
Если x^
a(x)
нс возрастает па.
R
+
для иск второго
y
€ R
такого. что к-
(min{1,
y
}) < то,
то kK-
1|
р),
6
к1
(min{1,
y
}
).
Если xx
a(x)
не убываст па
R
+
для иск второго
А
€
R
La
(R
+
)
такого, что к
+
(тах{1,А}) < то, т
о
||K +kLP
)
(r
)
6 к
+
(тах{1, А}).
III.
Пусть a
€ L
1
(R
+
).
Е<_зти K
-(x,y) > 0 в
случае (эпсратора K- 11 K
+(x,y) > 0 в случае оператора
K
+, то
условия к-< то и к+< то необходимы для ограниченности операторов K
-
и K
+ соответственно
в гранд-пространстве
Lp)(R
+
) н при этом
IV.
В случае грандизатора
a(x) = x-A(1 + x)A-Y, A,
y
€ R,
условия к-
(min{1, Л,
y
}) < то
11 к+
(max{1,A,
y
}
)
< то
достало1 шы. при K
-(x,y)
>
0
ii K
+ (x,y) > 0
условия к-
(max{1, A}) <
to
ii к+
(min{1,
y
}) < то
необходимы для оградпчсппостп операторов K
-
и K
+ соответственно
в гранд-пространстве
L^
)
(R+)
и при этом справедливы оценки
K-(max{1,A}) 6
kK
-kLp
)
(R+) 6 к-(min{1,A,Y}), (7)
к+ (min{1,Y}) 6
kK
+kLp
)
(R+) 6 к+(max{1,A,Y}). (8)
В частности, при
A =
y
= 1- K-(x,y) > 0
i1 K
+(x,y) > 0 онера
торы K
-
i1 K
+
ограничены в гранд-пространстве
L^
)
(R
+
) тогда
и только тогда, когда к-
< то
и к+
< то
соответственно, при этом ^K
-||
тР)
= к-
ii
||K+1| p) = к+.
La
(
R
+
)
La
(
R
+
)
<1 I. Докажем первое неравенство в (5), второе доказывается аналогично. Так как
K- f
(x) =
J1 K
-(1,t)f (xt)
dt,
то силу неравенства. Минковского в
Lp-5
получим
∞
kK f
kLP-pR+,a p
)
j
|K (1,t)| *
j If
(ty)|p ea(y)
p dy
i
p-ε
dt о о
=
j
|K-(1,t)|t M7 о
∞ j If (ПГ-П (x) p <0 dx
1
p-ε
dt
=
j
|K-(1,t)|t
p-E<
о
6
j
|K-(1,t)|t-p-7a* о
∞ j If (x)\p-ea(x)p 0 ε alti p a(x) dx ε
1 \
p^p-e)
t dt
1
p-ε
∞ j If (x)|p-ea(x)p dx , о dt
1
p-ε
После инверсии в первом интеграле можно получить доказываемое неравенство.
II. Докажем опенку для |K-| p) В силу свонтва растяжения (ag) имсм a*(t) 6 La (R+ )
t-Y nj)ii
t >
1. Поэтому
∞
—
1
eY
|K -kLp>(R+) 6 06™ 1/ lK - (t' ''I t Опенка для |K +|Lp)(R ) получается аналогично. Lp (R+ ) K- ство функций в виде -1+8 f8 (x) = |x p ’ 0 < x 6 1, x > 1. Так как fg € Lp(R+) и a € L1(R+), то fg € La)(R+) в силу (2). Из ограниченности оператора K- в гранд-пространстве La)(R+) следует, что он определен на функции fg. При x < 1 плюем K ffs (x) = У о K (1, t)fs(xt) dt > Kp(6)fs(x), где Kp(6) = R1 K (1,t)fs(t) dt. Следовательно. \\K-II > kK fkLp)(R+) > Kp(6). k kLp)'^ > IfkLp)(R+) Остается перейти к пределу при 6 ^ 0 под знаком интеграла, определяющего кр(6), что обосновывается теоремой Леви. Оценка нормы оператора K+ доказывается аналогично. IV. Правые оценки в (7) и в (8) получается из (5) непосредственными вычислениями с учетом того, что в этом случае справедливо равенство (см. пример 2.1) a* (x) = {t-max{A,Y} t-*}, 0 < t 6 1, t > 1. Получим оценку снизу нормы ||K ||lp)(r ). функций в виде fs (x) = {Г^’ Возьмем минимизирующее семейство 0 < x 6 1, x > 1, где 6 > 0, v = 1 — map1^} цмеем kfs kLP)(R+) sup ep-E 0 dx xvP+ f 'X-vpt-S'p-e) 0 1 p-ε Отсюда простыми рассуждениями получаем, что fs Е Lp) (R+) Оценим K fs поточечно 0 Kffs(x) = KX-(1,t)fs(xt) dt = x-v+s о У K-^tK+sd dt о Отсюда получаем 1 x = fs(x) У K-(1,t)t о v+s dt > fs(x) jx-(1,t)t-v+s dt. »K’ kL?'R+) > kK fs kLP) (R+) kfs kLP)(R+) > У K-(1,t)t-v+s dt. о Чтобы получить оценку снизу для ||K |l p),m . остается пере!гти к пределл- при 6 ^ 0. a(R+) Предельный переход под знаком интеграла возможен в силу теоремы Леви. Оценка снизу для ||K +kLp)(R+) получается аналогично посредством функции fs (x) = x µ δ, 0 < x 6 1, x > 1, min{1,Y} где о > 0. ц = 1 - p—. B 4. Многомерный случай 4.1. Случай радиального ядра. Оценки через сферические средние. В этом пункте мы рассмотрим случай радильных ядер k-(|x|, |y|) и k+(|x|, |y|). В этом случае мы K- K+ гранд-пространстве. Именно, мы получим оценки для норм ||K- f || р) и ||K+f || р) La (Rn) La (Rn) через сферические средние F(Р):= |SMT| / f(pa) da Sn-1 функции f (см. теорему 4.1). a А(Р) := Р Е R+ |^-Т| / а(Ра) da’ Sn-1 Многомерные оператор K и K+ сводятся к одномерным операторам K и K+ с ядрами k- ii к+ по формулам K -f (x) = K-F (|x|), K+f (x) = K+F (|x|), (9) где k-(p, r) = |Sn-1|pn-1k-(p,r) 1i k+(p, r) = |Sn-1|pn-1 k+(p, r). что позволит воспользоваться результатами для одномерного случая на основании доказываемой ниже леммы 4.1. Отметим следующие следствия из неравенства Несена: Sn-1 IF(p)lq6 TS^ / Sn-1 Лемма 4.1. Справедливы неравенства «K -f «Lp)(Rn) 6«KK-F «LpA)(R+), |f (pa)|q da, q > 1. 1K +f ^Lp)(R.) 6 «K+F«t;?(R+)- где ∞ K F(p) = I - (p,r)F(r) dr, 1 n-1 F^(p) = |Sn-1|pp — F (p), ∞ KK+F(p) = у fc+(p,r)F(r) dr, 0 -4(p) = |S”-1|p"-1A(p), ^^ k-(p, г) = |Sn 1| fpprp0 n—1 k-(p, r), 1 1 \n-1 । k+ (p, r) = |Sn Hpprp0 j k+ (p,r). C Согласно (9) имеем У |K f (x) |p ea(x) p dx = Rn ∞ j pn—1 K- F (p) |p- J 0 Sn-1 ε a(p^) p d^dp. Тогда в силу (10) ∞ j |K—f (x) |p ea(x)p dx 6 |Sn—11j pn—11K—F(p) |p eA(p)p dp. Rn 0 Отсюда прямыми преобразованиями приходим к первому неравенству в (12). Второе B Лемма 4.2. Для радиальной функции f справедливо соотношение kfkLp)(Rn) 6 kfkLA(Rn), где A(x) := iS1-^ JSn-1 a(|x|a) da. C Для доказательства достаточно в левой части применить неравенство (10), перейдя B Следующая лемма доказывается аналогично с помощью неравенства (11). Лемма 4.3. Пусть A(x) = A(|x|). Тогда kFkLpA(Rn) 6 kfkLA(Rn), тле F(x) := |sn-ii JSn-i f (|x|a) da. В следующей теореме мы рассматриваем неравенства вида kK-f kL»(Rn) 6 C -kF kLA (Rn), IK+ f kLj'(«n) 6 C+kF kLA (Rn), (14> где F(x) = F(|x|), a — произвольный грандизатор на Rn, сферическая средняя которого равна функции A(x) = A(|x|), а также даем оценки снизу и сверху для наилучших константC—I ic+b(14). Обозначим ∞ ε 1A*(t)p(p-E) dt, ε 1A*(t)p(p-E) dt, d—(A) := |Sn—11 sup [ |k— (t, 1) | tpn^ 0 1 d+(A):=| Sl—11 sup [ | k+ (t, 1) | t p-^ 0 κn ∞ := j| k-(1,y)|yn 1dy, Kn := j|k+ (y, 1)|yn-1dy. Теорема 4.1. Пусть 1 < p < то, A(|x|) — грандизатор на Rn, функции k (|x|, |y|) и k+(|x|, |y|) однородны степени —n. I. Если d-(A)< то, d+(A) < то, то неравенства (14) выполняются с C- = d-(A) п C + = d+ (A) соответственно. II. Если tY A(t) не возра стает па. R+для пекоторого y € R таков о. что K-(min{n, y})< то, то C- 6 |Sn-1|K-(min{n, y})• E<.мп txA(t) не убывает па R+для пекоторово А € R таково, пто к+(тах{п, А}) < то, то C+ 6 |Sn-1|K+(max{n, А}). III. Если A € L1(Rn) 11 k-(|x|, |y|) > 0. k+(|x|, |y|) > 0. то ус-ловня к-< то. к+ < то необходимы для отрадпчеппостп операторов K- ii K- соответственно в грапд-пространстве Lp)(R+). При этом для наилучших констант в неравенствах (14) справедливы оценки |Sn->- 6 C-, |Sп-1|к+ 6 C+.(15) IV. При a(x) = |x|-A(1 + |x|)A-Y, A,y € R, и неотрицательных ядер наилучшие константы в (14) удовлетворяют неравенствам |Sn-11к- (max{n, А}) 6 C- 6 |Sn-11K-(min{n, A,y}),(16) |Sn-11K+(min{n,Y}) 6 C+ 6 |Sn-11K+(max{n, А,7})•(17) В частности, при А = y = n имеют место равенства C-- = | Sn-11 к-, C+ = | Sn-11 к+ ∗ n∗n C Доказательство теоремы подготовлено леммой 4.1. Применяя теорему 3.1 в правых частях неравенств (12), после ряда простых преобразований получаем утверждение теоремы в достаточной части. Для получения оценок норм снизу в пунктах III и IV неравенства (12) неприменимы. Но мы воспользуемся тем, что на радиальных функциях неравенства (10) и (11), а следовательно, и неравенства (12), превращаются в равенства. Получим первую оценку из (15). Рассмотрим минимизующую функцию , , х \|x| p +, 0 < |x| 6 1, fg(x) = 0, |x| > 1, где 5 > 0. Очевидио fg € Lp(Rn) ii. следовательно, в силу включения A € L1(Rn). fg € Lp)(Rn). Ввиду радиальности fg имеем kK fgkLA)(Rn) WK Fg HlA)(R+) , 1 n__1 где ?l(p) = |Sn-1|pn-1A(p), .Fg(p) = is;^^ RSn_i fg(pa) do = |Sn-1|pp p fg(p). Воспользовавшись первым из неравенств (6), после несложных преобразований по лучим WK fg WLA)(Rn) > К- WFgIIlA)(R+) |S |Kn kfg kLpA (Rn). Тем самым первое из неравенств (15) доказано. Второе получается аналогично посред ством функции fg(x) = 11 ’,-n-g 0 < |x| 6 1, |x| > 1, |x| p , где 5 > 0. Доказательство неравенств (16) и (17) аналогично доказательству неравенств (7) ii (8). в 4.2. Общий случай. Обозначим КР:= / |x|61 K (ei, x) -—р dx, Г(о):= sup [ |K- (x^lM™^ dx. 0 |x|>1 Заметим, что ' (a) 6 J|x|>1 |K (x,e1)| max [a. (|x|)] р(р—) Ч11СЛС1ШСМ SUPo<e<p-1J n —. |x| (Р—Д* I ЫЫ)]p0 n |x| p0 dx, Теорема 4.2. Пусть 1 < p < то, a = a(|x|), я/тро K (x,y) однородно степени —n и инвариантно относительно вращений. Если '-(a) < то, то оператор K- ограничен в гранд-пространстве L^)(Rn) н IKНд)№ 6 Г (a)- Если K (x,y) > 0 na G L1(Rn), то условие кр< то необходимо для такой ограниченности и Kp6kK kLp)(Rn)- C Оценим ||K f kLp-e(Rn ap) сверху. Для этого представим K f (x) в виде k-f(x)= j |y| qn K-(x,y) 1 |y|6|x| E a(|x|) p E a(|y|)p ) qq0 n |y|qq0 K (x,y)q E a(|y|)p E a(|x|) p ! f (У) dy- Применяя неравенство Гёльдера, получим |K-f (x)| 6 {A}7 j |y|n|K-(x,y)| Jy|6|x| E a(|y|)p E a(|x|) p q q If(y)|qdy > , A = |x| p-E j |y| |y|61 n p-ε K x |x|,y Е a(|y|) ■■ a(|x||y|) y- В последнем интеграле сделаем замену вращения y = w(z), при котором ш(е1) = |Х|, где e1 = (1, 0, - - - , 0), a(t) sUP3AJT t<1 a(xt) 6 a∗ x x > 0, K А 6 |x| p j |y| p K (ei,y)| |y|6i a* ε p(p-E) dy. _ n Сделав в интеграле преобразование инверсии, получим А 6 |x| p-E'~(a), где ε ЩО):= [ |K_ (x,ei)' pp dx. |x|(p-E)0 |x|>1 Таким образом, получаем | K-f (x) | 6 ['-(a)] (p-)7 n |x| (p-e)(p-e)0 ■ у |yl . |y|6|x| n (p-E)0 |K-(x,y)| aCM)p a(|x|) p 1 (p-E)0 1 p-ε |f . dy\ Далее, имеем kK-fkLp ε Rn,ap 6 ['-(a)] (p-E)0 |f . x (p-E)0 n x j |x| (p-E)0 |K (x,y)| a(|y|) p a(|x|) p (p-e)0 a(|x|)p dxdy p-ε |y|6|x| =['-(a)] <p—7 nε (p-E)0 a(|y|)p(p-E)0 |x| nε (p-E)0 |K-(x,y)|a(|x|)p(p-E)dxdy 1 p-ε . |y|6|x| После замены x ^ |y|x и вращения во внутреннем интеграле, получим 1 I Г E kK-fkLp-E/RпДА 6 ['-(a)](p-E)0 |f(y)|p-ea(|y|)p(p—T dy L R ,ap Rn x У |x| |x|>1 П E p-E (p-E)0 |K (x,e1 )|a(|x||y|)p(p-E)dx ['-(a)] ~ |f(y)|p ea(|y|)pdy x У |x| (p-E)0 |K (x,e1 )| |x|>1 a(|x||y|) p(p-E) a(|y|)У dx ) p—E 6 ['-(a)] (p—T Ilf || , ex ε Lp-ε Rn,ap |x| nε (p-E)0 |K-(x, e1 )| [a*(|x|)]p(p-E) dx ^ p—E 1 1 ['-(a)] (p-E)0 ['-(a)]p^ ||f || , ex = '-(a)|f II , ex . ε ε Lp-ε Rn,ap ε Lp-ε Rn,ap Отсюда с учетом (1), приходим к (18). Для доказательства оценки снизу в (19) возьмем минимизирующее семейство функций в виде fs(x) = |x|-П+s(1 + |x|)-2^. Так как fs E L-(Rn) 1i a E L1 (Rn). то fs E La) (Rn) в силу (2). Из ограниченности оператора K- в гранд-пространстве La)(Rn) следует, что fδ K -fs (x) = I |y|6i К (ei,y)fs(|x|y) dy. Легко проверить, что fs(xy) > fs(x)fs(y) Тогда K fs(x) > к-(б) f5 (x), где к- (б) = J|y|61 К (ei, y)fs(y) dy. Следовательно. kK kLP)(Rn) > kK fs kLP)(Rn) kfs ^LP) (Rn) >к- (б) Остается перейти к пределу при б ^ 0 под знаком интеграла, определяющего кр (б), что обосновывается теоремой Леви. B Аналогичное утверждение справедливо и для оператора K+ с заменой к- и '-(а) на к+ /К+ (x, e1) —n dx |x| p0 |x|>1 И '+(a) = sup 0 У |К+ (e1, x) | |x| |x|61 n ε p - [a* (|x|)] p(p-E) dx соответственно. Автор выражает благодарность профессору С. Г. Самко за. полезное обсуждение результатов работы и анонимному рецензенту за. цепные замечания.
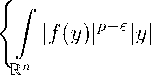
Список литературы Односторонние интегральные операторы с однородными ядрами в гранд-пространствах Лебега
- Крейн С. Г., Петунин Ю. И., Семенов Е. М. Интерполяция линейных операторов. М.: Наука, 1978. 499 с.
- Умархаджиев С. М. Ограниченность линейных операторов в весовых обобщенных гранд-пространствах Лебега//Вестн. Акад. наук Чеченской респ. 2013. Т. 19, № 2. С. 5-9.
- Умархаджиев С. М. Обобщение понятия гранд-пространства Лебега//Изв. вузов. Математика. 2014. Т. 4. C. 42-51; пер. на англ.: Generalization of the notion of grand {Lebesgue space. Russian Math. (Iz. VUZ). 2014. Vol. 58, № 4. P. 35-43.
- Умархаджиев С. М. Ограниченность потенциала Рисса в весовых обобщенных гранд-пространствах Лебега//Владикавк. мат. журн. 2014. Т. 16, № 2. C. 62-68.
- Умархаджиев С. М. Плотность пространства Лизоркина в гранд-пространствах Лебега//Владикавк. мат. журн. 2015. Т. 17, № 3. C. 75-83.
- Iwaniec T., Sbordone C. On the integrability of the Jacobian under minimal hypotheses//Arch. Rational Mech. Anal. 1992. Vol. 119. P. 129-143.
- Karapetiants N. K., Samko S. G. Equations with Involutive Operators. Boston: Birkhauser, 2001.
- Kokilashvili V., Meskhi A., Rafeiro H., and Samko S. Integral Operators in Non-standard Function Spaces. Vol. I. Variable Exponent Lebesgue and Amalgam Spaces. Basel: Birkhauser, 2016. 1-586 p. (Operator Theory: Advances and Appl. 248).
- Kokilashvili V., Meskhi A., Rafeiro H., and Samko S. Integral Operators in Non-Standard Function Spaces. Vol. II. Variable Exponent Holder, Morrey-Campanato and Grand Spaces. Basel: Birkhauser, 2016. 587-1009 p. (Operator Theory: Advances and Appl. 249).
- Samko S. G. Hypersingular Integrals and their Applications. London-N.Y.: Taylor & Francis. 2002. 358+xvii p. (Ser. Analytical Methods and Special Functions. Vol. 5).
- Samko S. G., Umarkhadzhiev S. M. On Iwaniec-Sbordone spaces on sets which may have infinite measure//Azerb. J. Math. 2011. Vol. 1, № 1. P. 67-84.
- Samko S. G., Umarkhadzhiev S. M. On Iwaniec-Sbordone spaces on sets which may have infinite measure: addendum//Azerb. J. Math. 2011. Vol. 1, № 2. P. 143-144.
- Samko S. G., Umarkhadzhiev S. M. Riesz fractional integrals in grand Lebesgue spaces//Fract. Calc. Appl. Anal. 2016. Vol. 19, № 3. P. 608-624.
- Samko S. G., Umarkhadzhiev S. M. On grand Lebesgue spaces on sets of infinite measure//Math. Nachrichten. 2016. URL: http://dx.doi.o DOI: rg/10.1002/mana.201600136
- Umarkhadzhiev S. M. The boundedness of the Riesz potential operator from generalized grand Lebesgue spaces to generalized grand Morrey spaces//Operator Theory, Operator Algebras and Appl. Basel: Birkhauser/Springer, 2014. P. 363-373.


