анализе называется теорией двойственности; такое же название носит теория характеров в теории локально компактных групп и т. д.). Общие наблюдения позволяют сказать, что в основе понятия двойственности лежит понятие дуальной пары { X, Y ) — пары пространств, обладающих зеркальными (двойственными) свойствами. Обнаружение дуальных пар является основной задачей общей теории двойственности . При этом теоремы, утверждающие дуальность конкретных пар, называются теоремами двойственности . Наличие дуальной пары позволяет осуществлять двойственные переходы — переносы конкретных математических высказываний из одной области в другую путем зеркальной (формальной) переформулировки. Эти переформулировки бывают и очень сложными, но сводятся к замене внутренных (инъективных) описаний множеств внешними (проективными) описаниями двойственных им множеств и наоборот. Инъективное описание множества — описание множества по какой-либо совокупности его подмножеств. Проективное описание множества — описание множества по какой-либо совокупности его надмножеств. Описание множества — композиция из инъективных и проективных описаний. Подобно тому как формула (композиция операций) наследует название последней выполняемой операции, любое описание множества является либо инъективным, либо проективным.

Таким образом, возникает новое понимание двойственных переходов как переходов от инъективных (соотв. проективных) описаний множеств к проективным (соотв. инъективным) описаниям двойственных им множеств. Правила (отображения), используемые при описании множеств, называются дескрипторами . Дескрипторы инъективного описания называются интериоризаторами , а дескрипторы проективного описания называются экстериоризаторами .

В качестве примера рассмотрим произвольные многозначные отображения F : X ^ Y и G : Z ^ T . При заданных F и y o G Y задача описания прообраза F - 1 (У о ) (если отображение F является однозначным, то эта задача совпадает с классической задачей решения уравнения F (x) = y o ) является задачей инъективного описания. Ее решение предполагает переход от проективного описания (экстериоризатор — F) к инъективному описанию (интериоризатор — объединение). С другой стороны, пусть G ^{- 1} : T ^ Z — обратное многозначное отображение. При заданных G ^{- 1} и z o G Z задача описания образа G(z o ) является задачей проективного описания. Ее решение предполагает переход от инъективного описания (интериоризатор G ^{- 1} ) к проективному описанию (экстериоризатор — пересечение). Если отображения F и G находятся в определенной дуальной зависимости, то и рассмотренные здесь задача инъективного описания и задача проективного описания находятся в дуальной зависимости. Этот пример показывает, что при новом понимании двойственных переходов центральным объектом выступает уже дуальная пара отображений F, G ^{- 1} — дуальная пара дескрипторов . Исследование дуальной пары дескрипторов в классическом понимании равносильно исследованию упорядоченной совокупности из двух дуальных пар { X, Y} и { Z, T ) или одной бипары {{ X, Y ) , { Z, T )) .

Теоремы двойственности являются двусторонними. Они позволяют осуществлять двойственные переходы в одну и другую стороны. Наличие такой теоремы создает идеальные условия для применения взаимно обратных двойственных переходов в конкретной исследовательской практике. В этом состоит основное значение теорем двойственности. Основным недостатком теорем двойственности является их неширокая область применения. Предполагаемая возможность прямого и обратного двойственных переходов вынуждает накладывать на дуальные пары значительные ограничения, и это влияет на область их возможного использования.

В настоящей статье утверждается возможность односторонних теорем двойственности, которые предполагают двойственные переходы только в одну сторону. Такие теоремы мы называем односторонними схемами двойственности . Дуальные пары, используемые в односторонних схемах двойственности, в свою очередь являются односторонними, и налагаемые на них ограничения существенно слабее. Это приводит к существенному расширению области возможного применения двойственных схем.

В основе односторонней теории двойственности лежит понятие вполне изотонного отображения и условно обратного к нему отображения. Определение и примеры вполне изотонных отображений приведены в разделе 2. Свойства вполне изотонных отображений исследованы в разделе 3. Раздел 4 посвящен строгому определению дескрипторов и дуальных дескрипторов. Здесь же рассмотрена дуальная взаимозависимость ин-териоризаторов и экстериоризаторов (предложение 4). В разделе 5 определены задачи инъективного и проективного описаний, показана их дуальная взаимосвязь и доказана основная односторонняя схема двойственности (теорема 1). В разделе 6 рассмотрен частный случай, в котором односторонняя схема двойственности допускает взаимно обратные двойственные переходы (теорема 2). Содержание этого раздела наиболее близко к классическому пониманию общей теории двойственности.

Понимание двойственных переходов как переходов от описания одного характера к описанию другого характера возникло в условиях задачи спектрального синтеза в комплексной области [1–4]. Эти исследования опираются на свойства дуальной бипары (( H, H * ) , ( P, P * )) , где H : = H(Q) — пространство аналитических функций, H * — его сильное сопряженное пространство, P : = P q — интерпретация H * в терминах оператора Лапласа, P ^∗ — его сильное сопряженное пространство. Двойственные переходы в условиях этой бипары осуществлялись неоднократно и при решении разных задач [5–16].

• 2.    Вполне изотонные отображения

  • 2.1.    Терминология и обозначения. Декартово произведение _{λ ∈ Λ} X λ семейства множеств { Х д : А € Л } обозначаем Х л . Элементы декартова произведения Х л обозначаем х л := (х д : А € Л). Декартову степень П д _е л X множества X обозначаем X ^л . Декартово произведение X Λ частично упорядоченных множеств всегда рассматриваем как частично упорядоченное множество с порядком: х л С Х л тогда и только тогда, когда х Д С х д для любого А € Л. Замечаем, что порядок в декартовом произведении Х л является обратным по отношению к порядкам в множествах { Х д : А € Л } . Например, если Л состоит из одного элемента Л = { 0 } , то Х л совпадает с множеством Х о , в котором порядок заменен обратным порядком.

Отображения отождествляем с непустыми однозначными бинарными отношениями. Для обозначения отображения m, действующего из множества X в множство Y , используем обычный символ m : Х ^ Y. Область определения (соответственно область значений) отображения m обозначаем символом Dom m (соответственно Im m). Если Dom m = Х, то пишем m : Х н- Y. Сужение m|x0 отображения m : Х ^ Y на множество Хо определяется как отображение n : Х ^ Y, удовлетворяющее условиям: Dom n = Хо П Dom m и п(х) = m(x) для любого х € Dom n. Областью определения (соответственно областью значений) семейства {mд : А € Л} отображений mд : Хд ^ Yд называем пересечение Dom{mд : А € Л} := Пдгд Dommд (соответственно объединение Im{mд : А € Л} := идел Im mд). Декартовым произведением семейства отображений {mд : А € Л} называется отображение mл : Хл ^ Yл | (хд : А € Л) ^ (mд(xд) : А € Л).

Область определения декартова произведения mΛ совпадает с декартовым произведением Плел Dom mA- Декартовой степенью отображения m : X ^ Y называется отображение mл : Xл ^ Yл | (хд : А Е Л) н- (m(x^) : Л Е Л).

Область определения отображения m ^л совпадает с декартовой степенью (Dom m) ^л .

Говорим, что отображения m : X ^ Y и n : Z ^ T совпадают (имеет место функциональное равенство m = n), если Dom m = Dom n и m(x) = n(x) для любого x Е Dom m. Говорим, что на множестве X o имеет место функциональное равенство m = n (отображения m и n совпадают на множестве X o ), если m | x ₀ = n | x ₀ . Символом X(m = n) (соответственно X(m C n)) обозначаем множество

{ x Е Dom { m, n } : m(x) = n(x) }

(соотв. { x Е Dom { m, n } : m(x) C n(x) } ).

При фиксированном z Е Dom n (соответственно x Е Dom m) символом X(m(x) C n(z)) (соответственно Z (m(x) C n(z)) обозначаем множество

{ x Е Dom m : m(x) C n(z) } (соотв. { z Е Dom n : m(x) C n(z) } )

Композиция n о m отображений n и m определяется как отображение X ^ T | x ^ n(m(x)) с областью определения

Dom(n о m) := { x Е Dom m : m(x) Е Dom n } .

При рассмотрении произвольной композиции n о m всегда предполагаем, что выполнено условие ее существования Im m П Dom n = 0 .

• 2.2.    Вполне изотонные отображения. Отображение m : X ^ Y , где X, Y — частично упорядоченные множества, называется изотонным, если для любых x i ,x 2 Е Domm, удовлетворяющих условию x i C x 2 , выполнено неравенство m(x i ) C m(x 2 ). Элемент у Е Y называем частичной мажорантой (соответственно частичной минорантой ) изотонного отображения m : X ^ Y , если множество X(m(x) C у) (соответственно X(у C m(x))) не является пустым. Согласно этому определению любая точка из области значений Im m является и частичной мажорантой, и частичной минорантой отображения m. Если элемент у Е Y является частичной мажорантой (соответственно частичной минорантой) изотонного отображения m : X ^ Y и у C у ' (соответственно у' C у), то элемент у' Е Y тоже является частичной мажорантой (соответственно частичной минорантой) отображения m.

Изотонное отображение m : X ^ Y называем инъективным (соответственно проективным ), если выполнены условия:

• 1)    если x,x ' Е X, x C x ' (соответственно x ' C x) и x Е Dom m, то x ' Е Dom m;

• 2)    для любой частичной мажоранты (соответственно частичной миноранты) у Е Y отображения m множество X(m(x) C у) (соответственно X(у C m(x))) обладает наибольшим (соответственно наименьшим) элементом.

• 2.3.    Примеры вполне изотонных отображений. Вполне изотонные отображения встречаются часто. Рассмотрим еще четыре примера вполне изотонных отображений.

Инъективные и проективные отображения называем вполне изотонными отображениями. Множество Xo С X, обладающее свойством x C x', x' Е Xo ^ x Е Xo (соотв. x' C x, x' Е Xo ^ x Е Xo), принято называть прямым (соответственно обратным) порядковым идеалом. Значит, по определению вполне изотонного отображения область его определения является порядковым идеалом. Отмечаем, что при замене порядков в множествах X и Y их обратными порядками инъективное (соответственно проективное) отображение m : X ^ Y становится проективным (соответственно инъективным) отображением.

Понятие вполне изотонного отображения напрямую связано с понятием многозначного отображения (непустого бинарного отношения). Поясним это утверждение. Пусть A, B — множества, X := (X, С ), Y := (Y, С ) — их булеаны соответственно. Многозначное отображение F : A н- B можно рассматривать как однозначное отображение m : X ^ Y | x н- F (x), где F (x) G Y — образ множества x С A. При этом, если Dom F = A, то отображение m является инъективным. Действительно, в этом случае Dom m = X, отображение m является изотонным и для любой частичной мажоранты y G Y отображения m множество X(m С у) обладает наибольшим элементом. Этим элементом является прообраз F - 1 (у) множества у С B.

С другой стороны, всякое многозначное отображение F : A ^ B имеет многозначное обратное отображение F - 1 : B ^ A, которое каждому b G Im F ставит в соответствие прообраз F - 1 (b). Обратное многозначное отображение F - 1 : B ^ A можно рассматривать как однозначное отображение n : Y ^ X | у н- F ^{- 1} (у), где F ^{- 1} (у) G X — прообраз множества у С B . При этом, если Im F = B , то отображение n является проективным. Действительно, в этом случае Dom n = Y , отображение n является изотонным и для любой частичной миноранты x G X отображения n множество Y (x С n) обладает наименьшим элементом. Этим элементом является образ F (x) множества x С A.

Пример 1. Пусть X, Y — частично упорядоченные множества. Порядковый изоморфизм m : X н- Y является инъективным и проективным отображением одновременно. Его условно обратное отображение совпадает с обратным отображением.

Пример 2. Пусть X С R . Действительная возрастающая функция m : X н- R осуществляет инъективное (соответственно проективное) отображение X н- R тогда и только тогда, когда она полунепрерывна снизу (соответственно полунепрерывна сверху).

Пример 3. Пусть ( A, B) — дуальная пара векторных пространств над полем R или C ; X := (X, С ), Y := (Y, D ) — булеаны множеств A и B соответственно. Полярой x ⁰ множества x G X называется абсолютно выпуклое слабо замкнутое множество элементов b G B , для которых | ( a, b ) | С 1 при любом a G A. Поляра у ⁰ множества у G Y определяется симметрично и состоит из элементов a G A, для которых | ( a, b ) | С 1 при любом b G B. Отметим элементарные свойства поляр:

1 ° . если x 1 ,x ₂ G X и x 1 С x ₂ , то x ⁰ С x ⁰ ;

2 ° . если у 1 ,у 2 G Y и у х С у 2 , то у 0 С у ⁰ ;

3 ° . если x G X и x ⁰⁰ = (x ⁰ ) ⁰ , то x С x ⁰⁰ ;

4 ° . если у G Y и у ⁰⁰ = (у ⁰ ) ⁰ , то у ⁰⁰ С у.

Рассмотрим отображения m : X ^ Y | x ^ x ⁰ и n : Y ^ X | у ^ у ⁰ . По свойствам 1 ° и 2 ^° отображения m и n являются изотонными. При этом отображение m является инъективным. Действительно, если элемент у G Y является частичной мажорантой отображения m, то множество X(m(x) С у) обладает наибольшим элементом. Этим элементом является поляра у ⁰ . В самом деле, по свойству 4 ° у ⁰⁰ С у, значит, у ⁰ G X(m(x) С у). При этом, если x G X(m(x) С у), то x ⁰ С у и по свойствам 3 ° и 2 ° x С x ⁰⁰ С у ⁰ .

С другой стороны, отображение n является проективным. Действительно, если элемент x G X является частичной минорантой отображения п, то множество Y (x С m(y)) обладает наименьшим элементом. Этим элементом является поляра x ⁰ . В самом деле, по свойству 3 ° x С x ⁰⁰ , значит, x ⁰ G Y(x С m(y)). При этом, если y G Y(x С m(y)), то x С у ⁰ , и по свойствам 1 ° и 4 ° x ⁰ С у ⁰⁰ С у.

Пример 4. Пусть A — топологическая группа, B — группа характеров группы A, x — некоторая замкнутая подгруппа группы A. Множество x ⁰ всех элементов b G B , для которых b(a) = 0 при всяком a G x, называется аннулятором подгруппы x в группе B и представляет собой подгруппу группы B . Далее, пусть y — замкнутая подгруппа группы B . Множество у ⁰ всех элементов a G A, для которых b(a) = 0 при всяком b G у, называется аннулятором подгруппы y в группе A и представляет собой подгруппу группы A. Множества x ⁰ и y ⁰ являются замкнутыми подгруппами топологических групп B и A соответственно.

Пусть X := (X, С ), Y := (Y, D ) — совокупность всех замкнутых подгрупп A и B соответственно. Рассмотрим отображения m : X н- Y | x ^ x ⁰ и п : Y Н- X | у ^ у ⁰ . Свойства аннуляторов повторяют свойства поляр 1 ° -4 ° , сформулированные в предыдущем примере. Значит, отображение m является инъективным, а отображение n является проективным.

• 3.    Свойства вполне изотонных отображений

  • 3.1.    Условно обратные отображения. Пусть X, Y — частично упорядоченные множества. Всякое инъективное (соответственно проективное) отображение m : X ^ Y обладает условно обратным отображением m ^- : Y ^ X, которое каждой частичной мажоранте (соответственно частичной миноранте) у G Y отображения m ставит в соответствие наибольший (соответственно наименьший) элемент множества X(m(x) С у) (соответственно X(у С m(x))). Согласно этому определению область определения Dom m ^- С Y условно обратного отображения m ^- совпадает с множеством всех частичных мажорант (соответственно минорант) отображения m. При этом для любого вполне изотонного отображения m : X ^ Y выполняются включения:

Im m С Dom m ^- С Y, Im m ^- С Dom m С X, (1)

Свойство 1. Если m : X ^ Y —инъективное (соответственно проективное) отображение, то для любого у G Dom m- выполняется неравенство m о m-(y) С у (соотв. у С m ° m-(y)). (2)

• < 1 Пусть m : X ^ Y — инъективное (соответственно проективное) отображение. Выберем произвольный элемент у G Dom m ^- . По определению условно обратного отображения элемент m ^- (y) принадлежит множеству X(m(x) С у) (соответственно X(у С m(x))). Значит, выполняется неравенство m ° m ^- (y) С у (соответственно у С m ° m ^- (y)). >

Свойство 2. Если m : X ^ Y — инъективное (соответственно проективное) отображение, то для любого x G Dom m выполняется неравенство x С m- ° m(x) (соотв. m- ° m(x) С x). (3)

• <    Пусть x G Dom m и у := m(x). Замечаем, что x принадлежит множеству X(m(x) С у) (соответственно X(у С m(x))). Так как m ^- (у) —наибольший (соответственно наименьший) элемент этого множества, то справедливы соотношения x С m ^- (y) = m ^- ° m(x) (соответственно m ^- (y) = m ^- ° m(x) С x). >

Свойство 3. Если m : X ^ Y — вполне изотонное отображение, то условно обратное отображение m- : Y ^ X является изотонным.

• < 1 Действительно, допустим, что исходное отображение m : X ^ Y является инъективным (соответственно проективным). Пусть y i ,y 2 G Dom m - и y i С у 2 . Тогда имеет место вложение X(m(x) С y i ) С X(m(x) С У 2 ) (соответственно X(у 2 С m(x)) С X(y i С m(x))). Значит, m ^- (y ₁ ) G X (m(x) С у ₂ ) (соответственно m ^- (y ₂ ) G X(у 1 С m(x))) и по определению условно обратного отображения m ^- (y 1 ) С m ^- (y 2 )• >

Свойство 4. Если m : X ^ Y — вполне изотонное отображение, то для любого x G Im m- выполняется равенство m- о m(x) = x, а для любого y G Im m выполняется равенство m о m-(y) = у.

• <    Пусть m : X ^ Y — инъективное (соответственно проективное) отображение. Во-первых, выберем произвольный элемент x G Im m - . Найдется такой элемент у G Dom m - , что x = m ^- (y). Так как Im m - С Dom m, то x G Dom m и по свойству 1 m(x) = m о m ^- (y) С у (соответственно у С m о m ^- (y) = m(x)). С другой стороны, Im m С Dom m - , значит, m(x) G Dom m - и по свойству 3 m - о m(x) С m ^- (y) = x (соответственно x = m ^- (y) С m - о m(x)). Следовательно, по свойству 2 m - о m(x) = x.

Во-вторых, выберем произвольный элемент у G Im m. Найдется такой элемент x G Dom m, что у = m(x). Так как Im m С Dom m - , то у G Dom m - и по свойству 2 x С m - о m(x) = m ^- (y) (соответственно m ^- (y) = m - о m(x) С x). С другой стороны, Im m - С Dom m, значит, m ^- (y) G Dom m и в силу изотонности отображения m имеем у = m(x) С m о m ^- (y) (соответственно m о m ^- (y) С m(x) = у). Следовательно, по свойству 1 m о m - (у) = у. >

Свойство 5. Изотонное отображение n : X ^ Y является инъективным (соответственно проективным ) тогда и только тогда, когда существует изотонное отображение r : Y ^ X , удовлетворяющее условиям:

• 1)    Dom r совпадает с множеством всех частичных мажорант (соответственно минорант) отображения n;

• 2)    n о г(у) С у (соответственно у С n о г(у)) для любого у G Dom r;

• 3)    x С r о n(x) (соответственно r о n(x) С x) для любого x G Dom n.

Отображение r, удовлетворяющее условиям 1) 2) , 3) , и условно обратное отображение n ^- совпадают.

• <    Необходимость. Пусть n : X ^ Y — инъективное (соответственно проективное) отображение, n ^- — его условно обратное отображение. По определению условно обратного отображения отображение r := n - удовлетворяет условию 1). По свойствам 1 и 2 вполне изотонных отображений отображение r := n - удовлетворяет условиям 2) и 3).

Достаточность. Допустим, что существует изотонное отображение r : Y ^ X, удовлетворяющее условиям 1), 2) и 3). Покажем, что отображение n является инъективным (соответственно проективным). Выберем произвольную частичную мажоранту (соответственно частичную миноранту) у G Y отображения n и рассмотрим множество X(n(x) С у) (соответственно X(у С n(x))). Из условий 1) и 2) вытекает, что это множество содержит элемент г(у). При этом, если x принадлежит множеству X(n(x) С у) (соответственно X(у С n(x))), то по условию 1) n(x) G Imn С Domr. В силу изотонности отображения r получаем r о n(x) С r(y) (соответственно r(y) С r о n(x)). Значит, в силу условия 3) имеем x С r оn(x) С r(y) (соответственно r(y) С r о n(x) С x). Другими словами, элемент r(y) является наибольшим (соответственно наименьшим) элементом множества X(n(x) С у) (соответственно X(y(x) С n)). Это означает, что r(y) = n-(y) и отображение n является инъективным (соответственно проективным). Так как r(y) = n-(у) для любого у Е Dom r, то отображения r и n- совпадают. >

Свойство 6. Если отображение m : X ^ Y является инъективным (соответственно проективным ), то его условно обратное отображение m ^- : Y ^ X является проективным (соответственно инъективным ) и второе условно обратное отображение (m ^- ) ^- совпадает с отображением m.

• < 1 Пусть m : X ^ Y — инъективное (соответственно проективное) отображение, m ^- : Y ^ X — его условно обратное отображение. Покажем, что пара отображений n : = m ^- и r := m удовлетворяют условиям 1), 2) и 3) из формулировки свойства 5. Во-первых, пусть Dom(m ^- ) ^- — совокупность всех частичных минорант (соответственно частичных мажорант) отображения m ^- . Покажем, что Dom m = Dom(m ^- ) ^- . С одной стороны, если x Е Dom(m ^- ) ^- , то при некотором у Е Dom m ^- выполняется неравенство x С m ^- (y) (соответственно m ^- (y) С х)- При этом у — частичная мажоранта (соответственно частичная миноранта) отображения m, значит, m(x ’ ) С у (соответственно у С m(x ’ )) при некотором x ‘ Е Domm. Можно считать, что x ‘ := m ^- (y). Тогда x ‘ Е Im m ^- С Dom m и x С x ‘ (соотв. x ‘ С x). Значит, x Е Dom m и Dom(m ^- ) ^- С Domm. С другой стороны, пусть x Е Dom m и у := m(x) Е Domm ^- . Так как x Е X(m(x) С у) (соответственно x Е X(у С m(x))), то x С m ^- (y) = m ^- о m(x) (соответственно m ^- (y) = m ^- о m(x) С x), т. е. x — частичная миноранта (соответственно частичная мажоранта) отображения m ^- . Значит, Dom m С Dom(m ^- ) ^- и, следовательно, Dom m = Dom(m ^- ) ^- . Отсюда следует, что пара отображений n : = m ^- и r : = m удовлетворяют условию 1) из свойства 5.

Во-вторых, по свойству 1 для любого у Е Dom m ^- выполняется неравенство (2), а по свойству 2 для любого x Е Dom m выполняется неравенство (3). Следовательно, пара отображений n := m ^- и r := m удовлетворяют условиям 2) и 3) из свойства 5. Это означает, что условно обратное отображение m ^- является проективным (соответственно инъективным) и отображение m является условно обратным для отображения m ^- . >

Свойство 7. Если m : X ^ Y — инъективное (соответственно проективное ) отображение, то

X(m(x) С у) = X (x С m ^- (y)) (соотв. X(у С m(x)) = X(m ^- (у) С x)).

• <    Действительно, если m : X ^ Y — инъективное отображение и при некоторых x Е Dom m, у Е Y имеет место неравенство m(x) С у, то у — частичная мажоранта отображения m, значит, у Е Dom m ^- . Следовательно, m ^- о m(x) С m ^- (y) и по свойству 2 x С m ^- (y). С другой стороны, если при некоторых x Е X, у Е Dom m ^- имеет место неравенство x С m ^- (y), то у — частичная миноранта отображения m ^- , значит, у Е Dom(m ^- ) ^- . Но по свойству 6 (m ^- ) ^- = m, значит, у Е Domm. Следовательно, m(x) С m о m ^- (y) и по свойству 1 m(x) С у. Параллельное утверждение доказывается аналогично. >

• 3.2. Композиции вполне изотонных отображений. Продолжим рассмотрение свойств вполне изотонных отображений. Пусть X , Y , Z , T — частично упорядоченные множества.

Свойство 8. Если отображения m : X ^ Y и n : Y ^ Z являются инъективными (соответственно проективными ) , то композиция n о m является инъективным (соответственно проективным ) отображением из X в Z и его условно обратное отображение совпадает с композицией m ^- о n ^- .

• <1 По свойству 3 отображения m, n и их условно обратные отображения являются изотонными, значит, отображения n о m и m ^- о n ^- тоже являются изотонными. Осталось убедиться, что отображение n о m является инъективным (соответственно проективным) и его условно обратное отображение (n о m) ^- совпадает с отображением m ^- о n ^- . По свойству 5 для этого достаточно показать, что изотонное отображение m ^- о n ^- удовлетворяет условиям:

• 1)    Dom (m о n ) совпадает с множеством всех частичных мажорант (соответственно минорант) отображения n о m ;

• 2)    n о m о m ^- о n ^- (z) С z (соответственно z С n о m о m ^- о n ^- (z)) для любого z Е Dom (m ^- о n ^- );

• 3)    x С m ^- о n ^- о n о m(x) (соответственно m ^- о n ^- о n о m(x) С x) для любого x Е Dom (n о m).

Проверим выполнимость условия 1). Пусть Dom (n о m) ^- — множество всех частичных мажорант (соответственно минорант) отображения n о m и z Е Dom (n о m) ^- . Значит, множество X(n о m С z) (соответственно X(z С n о m)) не является пустым. Выберем произвольный элемент x из этого множества. Тогда по определению композиции m(x) Е Dom n и n о m(x) С z (соответственно z С n о m(x)), значит, z Е Dom n ^- . Отображение n является инъективным (соответственно проективным), значит, по свойству 2 m(x) С n ^- о n о m(x) С n ^- (z) (соответственно n ^- (z) С n ^- о n о m(x) С m(x)), значит, n ^- (z) Е Dom m ^- . Отсюда следует, что z Е Dom (m ^- о n ^- ). Следовательно, Dom (n о m) ^- C Dom (m ^- о n ^- ). С другой стороны, если z Е Dom (m ^- о n ^- ), то по определению композиции z Е Dom n ^- и n ^- (z) Е Dom m ^- . Из включения n ^- (z) Е Dom m ^- вытекает, что при некотором x Е Dom m выполняется неравенство m(x) С n ^- (z) (соответственно n ^- (z) С m(x)). Значит, по свойству 1 из включения z Е Dom n ^- следует, что n о m(x) С n о n ^- (z) С z (соответственно z С n о n ^- (z) С n о m(x)). Отсюда вытекает, что z Е Dom (n о m) ^- . Следовательно, Dom (m ^- о n ^- ) C Dom (n о m) ^- , т. е. Dom (m ^- о n ^- ) = Dom (n о m) ^- .

Покажем, что выполняется условие 2). Действительно, пусть z Е Dom (m ^- о n ^- ). Тогда m ^- о n ^- (z) Е Im m ^- C Dom m и по определению композиции n ^- (z) Е Dom m ^- . В силу инъективности (соответственно проективности) отображения m по свойству 1 выполняется неравенство m о m ^- о n ^- (z) С n ^- (z) (соответственно n ^- (z) С m о m ^- о n ^- (z)). Аналогично, в силу инъективности (соответственно проективности) отображения n выполняются неравенства n о m о m ^- о n ^- (z) С n о n ^- (z) С z (соответственно z С n о n ^- (z) С n о m о m ^- о n ^- (z)).

Далее покажем, что выполняется условие 3). Действительно, пусть x Е Dom (n о m). Тогда m(x) Е Dom n и n о m(x) Е Im n C Dom n ^- . В силу инъективности (соответственно проективности) отображения n по свойству 2 выполняется неравенство m(x) С n ^- о n о m(x) (соответственно n ^- о n о m(x) С m(x)). Аналогично, в силу инъективности (соответственно проективности) отображения m по свойству 2 выполняются неравенства x С m ^- о m(x) С m ^- о n ^- о n о m(x) (соответственно m ^- о n ^- о n о m(x) С m ^- о m(x) С x). >

Пусть m : X ^ Y, n : Y ^ Z, k : X ^ Z — произвольные вполне изотонные отображения; m-, n- , k- — их условно обратные отображения. Рассмотрим диаграммы

Y

Y

X

Z

Z

k-

X

Коммутативность этих диаграмм означает выполнение функциональных равенств к = п о т и к ^- = т ^- о п ^- соответственно. Справедливо следующее предложение.

Свойство 9. Если отображения m , n являются инъективными (соответственно проективными ) , то первая из представленных диаграмм коммутативна тогда и только тогда, когда вторая диаграмма коммутативна.

• <1    Предположим, что первая диаграмма коммутативна, т. е. k = п о т. По свойству 8 условно обратное отображение k ^- является вполне изотонным и совпадает с композицией т ^- о п ^- . Значит, вторая диаграмма тоже коммутативна. Далее предположим, что вторая диаграмма коммутативна, значит, к - = т ^- о п ^- . По свойству 8 (к - ) - = (п ^- ) ^- о (ш ), где (к - ) - , (п ^- ) ^- и (т ^- ) ^- — вторые условно обратные отображения. По свойству 6 отображения (к ^- ) ^- , (п ^- ) ^- и (т ^- ) ^- совпадают с отображениями к, п и т соответственно. Значит, к = п о т. Следовательно, первая диаграмма тоже коммутативна. >

Пусть к : X ^ Y , l : Z ^ T , т : Z ^ Y , п : T ^ X — произвольные вполне изо-тонные отображения; k ^- , l ^- , m ^- , n ^- — их условно обратные отображения. Рассмотрим диаграммы

Y

m

Z

Z

m

Y

k

X

T

l-

k-

TX

n

Из свойств 6, 7 и 8 легко вытекает справедливость следующих свойств.

Свойство 10. Если отображения k , l , n являются инъективными (соответственно проективными ) , то композиция т : = к о п о l является инъективным (соответственно проективным ) отображением и его условно обратное отображение m ^- совпадает с композицией l ^- о п ^- о к ^- .

Свойство 11. Если отображения k, l, n являются инъективными (соответственно проективными ) , то первая из представленных диаграмм коммутативна тогда и только тогда, когда вторая диаграмма коммутативна.

• 4.    Дескрипторы

  • 4.1.    Обозначения. Если высказываемое нами утверждение или определение сохраняет силу и для отображений из X в Y , и для отображений из Y в X , то при его записи будем использовать символ т : X ^ Y . Этот символ означает один из двух символов т : X ^ Y или т : Y ^ X. Символ т : X ^ Y называем первым значением символа т : X ^ Y , а символ т : Y ^ X называем вторым значением символа т : X ^ Y . При этом выбор значения символа т : X ^ Y осуществляется только один раз. При повторном использовании символа т : X ^ Y его значение остается прежним.

С символом т : X ^ Y свяжем два символа т ± : X ^ Y и т ^ : Y ^ X . Символ т ± : X ^ Y означает один из двух символов т : X ^ Y (первое значение) и т ^- : X ^ Y

(второе значение). При этом символ m ± : X ^ Y принимает первое (соответственно второе) значение, если символ m : X ^ Y принимает первое (соответственно второе) значение. Символ m ^ : Y ^ X означает один из двух символов m : Y ^ X (первое значение) и m - : Y ^ X (второе значение). При этом символ m ^ : Y ^ X принимает первое (соответственно второе) значение, если символ m : X ^ Y принимает второе (соответственно первое) значение.

В общем случае символы m : X ^ Y и m : Y ^ X равносильны. Необходимо исключить использование одного из этих символов. Для этого будем предполагать, что множества X и Y являются элементами некоторого простого ориентированного цикла

A --♦ B --* ... --♦ Z --* A, содержащего более двух различных элементов. Договоримся использовать символ m : X ^ Y только при условии, что множества X и Y являются соседними элементами этого цикла и X предшествует Y (в обозначениях X --* Y). Легко увидеть, что это соглашение исключает совместное использование символов m : X ^ Y и m : Y ^ X. Если множества X , Y и Z , T являются соседними элементами одного простого ориентированного цикла и X --* Y, Z --* T, то символ

(m, n) := (m : X ^ Y, n : Z ^ T )

означает один из четырех символов

(m : X ^ Y, n : Z ^ T ), (m : X ^ Y, n : T ^ Z ),

(m : Y ^ X, n : Z ^ T ), (m : Y ^ X, n : T ^ Z ).

Выбор значения символа (m, n) осуществляется только один раз и остается прежним в дальнейших построениях. Важно лишь то, что проводимые рассуждения не зависят от сделанного выбора.

• 4.2.    Дуальные пары. Пусть X, Y , Z и T — частично упорядоченные множества. Сформируем из этих множеств простой ориентированный цикл

X -- + Y --+ Z --+ T -- + X.

Выберем произвольные вполне изотонные отображения к : X ^ Y и 1 : Z ^ T . Пару (к,1) называем дуальной парой и обозначаем символом { к,1 ) . Дуальную пару { к, Г ) называем симметричной , если отображение k действует из X в Y , а отображение l действует из T в Z или, наоборот, отображение k действует из Y в X , а отображение n действует Z в T . Если дуальная пара { к, 1 ) является симметричной, то и зеркальная дуальная пара { 1, к ) является симметричной. Дуальные пары ( к ± ,к ^ ) и ( к ^ ,к ± ) тоже являются симметричными. Здесь отображение к ± : X ^ Y по определению совпадает с отображением k, если k действует из X в Y и, наоборот, совпадает с условно обратным отображением к ^- , если к действует из Y в X. Отображение к ^ : Y ^ X определяется симметрично. Оно совпадает с отображением k ^- , если k действует из X в Y и, наоборот, совпадает с отображением k, если k действует из Y в X .

Отметим, что по свойству 6 условно обратное к отображению k ^± совпадает с отображением k ^∓ и, наоборот, условно обратное к отображению k ^∓ совпадает с отображением k ^± , т. е.

(к ± ) ^- = к ^ ,   (к ^ ) ^- = к ± .

С другой стороны, используя свойство 6, легко убедиться, что справедливы и следующие соотношения:

(k - ) ± = k ± ,   (k - ) ^T = k T .

При этом, если отображение k ^± (соответственно k ^∓ ) является инъективным, то отображение k ^∓ (соответственно k ^± ) является проективным и, наоборот, если отображение k ^± (соответственно k ^∓ ) является проективным, то отображение k ^∓ (соответственно k ^± ) является инъективным.

• 4.3.    Дуальные отображения. Рассмотрим совокупность из двух ориентированных диаграмм

  m

  
  

  YZ

  XT

  
  

  n

  
  

  _Y m ^±

  
  

  k ^±

  
  

  X

  
  

  n ^∓

  
  

  Z

  
  

  l ^∓

  
  

  T

  
  
  
  

где ( k, l ) — дуальная пара вполне изотонных отображений k : X ^ Y и l : Z ^ T , ( m, n ) — симметричная дуальная пара вполне изотонных отображений m : Y ^ Z и n : T ^ X. Вполне изотонное отображение m : Y ^ Z называем дуальным к вполне изотонному отображению n : T ^ X относительно дуальной пары ( k, l ) , если для любого x G Dom n ' выполняется неравенство

Г о n ^T (x) <  m ± о k ± (x).

Выполнение этого неравенства означает, в частности, что Im n ' С Dom l, Dom n ' C Dom k ± и k ± (Dom n ^T ) C Dom m ± .

Рассмотрим другую совокупность из двух противоположно ориентированных диаграмм

XnT kl

YZ

n∓

T

m

k∓           l±

YZ m ^±

которые получены из диаграмм (4) с помощью горизонтальной симметрии. Вполне изо-тонное отображение n : X ^ T называем дуальным к вполне изотонному отображению m : Y ^ Z относительно дуальной пары (k, l), если для любого y G Dom m± выполняется неравенство l± о m±(y) ^ nT о kT(y).

Выполнение этого неравенства означает, в частности, что Im m ± С Dom l ± , Dom m ± C Dom k ' и k ' (Dom m ± ) C Dom n' .

При замене симметричной дуальной пары ( m, n ) симметричной дуальной парой ( m - ,n ^- ) вторые диаграммы в совокупностях (4) и (5) не меняются, значит, справедливо следующее предложение.

Предложение 1. Вполне изотонное отображение m : Y ^ Z (соответственно n : T ^ X) является дуальным к вполне изотонному отображению n : T ^ X (соответственно m : Y ^ Z ) относительно дуальной пары ( k,l ) тогда и только тогда, когда условно обратное отображение m ^- (соответственно n ^- ) является дуальным к условно обратному отображению n - (соответственно m ^- ) относительно дуальной пары ( k, l ) .

Предложение 2. Если вполне изотонное отображение m : Y ^ Z является дуальным к вполне изотонному отображению n : T ^ X относительно дуальной пары (k,l) и отображение m± : Y ^ Z является инъективным (соответственно проективным), то для любого х Е Dom n^ выполняется включение

Y(у С к ± (х)) С Dom m ± (соотв. Y (к ± (х) С у) С Domm ± ).

Если вполне изотопное отображение n : T ^ X является дуальным к вполне изо-тонному отображению m : Y ^ Z относительно дуальной пары ( к, 1 ) и отображение n ^ : X ^ T является инъективным (соответственно проективным ) , то для любого у Е Dom m ± выполняется включение

X(х С k ^ (y)) С Domn ^ (соотв. X(k ^ (у) С х) С Domn ^ ).

• <1 Во-первых, пусть вполне изотонное отображение m : Y ^ Z является дуальным к вполне изотонному отображению n : T ^ X относительно дуальной пары ( к, 1 ) и отображение m ± : Y ^ Z является инъективным. Выберем произвольное х из Dom n ^ . По определению дуального отображения выполняется неравенство

• 4.4.    Дескрипторы. Пусть Л — множество; X ^Л , Y ^л — декартовы степени частично упорядоченных множеств X и Y соответственно. Для любых х Е X и у Е Y символами х ^Л и у ^л обозначаем элементы (х : А Е Л) Е X ^л и (у : Л Е Л) Е Y ^Л соответственно. Сформируем из частично упорядоченных множеств X, X ^Λ , Y, Y ^Λ простой ориентированный цикл

1 ^ о n ^ (x) С m ± о к ± (х).

Значит, х Е Dom к ± и к ± (х) Е Dom m ± . Если у С к ± (х), то по определению инъективного отображения у Е Dom m ± , значит, Y(у С к ± (х)) С Dom m ± . С другой стороны, если отображение m ± : Y ^ Z является проективным и к ± (х) С у, то по определению проективного отображения тоже у Е Dom m ± , значит, Z (к ± (х) С у) С Dom m ± .

Во-вторых, пусть вполне изотонное отображение n : T ^ X является дуальным к вполне изотонному отображению m : Y ^ Z относительно дуальной пары ( к, 1 ) и отображение n ^ : X ^ T является инъективным. Выберем произвольное у из Dom m ± . По определению дуального отображения выполняется неравенство

1 ± о т ± (у) С n ^ о к ^т (у).

Значит, у Е Domк ' и к ^ (х) Е Domn ^ . Если х С к ' (у), то по определению инъективного отображения х Е Domn ^ , значит, X(х С к ' (у)) С Domn ^ . С другой стороны, если отображение n ^ : X ^ T является проективным и к ^ (у) С х, то по определению проективного отображения х Е Dom n ^ , значит, X(к ^ (у) С х) С Dom n ^ . >

X -^ Y -^ Y ^л --^ X ^л --^ X.

Вполне изотонные отображения F : X ^л ^ X и G : Y ^ Y ^л называем дескрипторами (на множестве X и Y соответственно). Дескриптор F : X ^л ^ X называем интерио-ризатором в точке х Е X, если отображение F ± : X ^л ^ X является инъективным, х ^л Е Dom F ± и выполняется неравенство

F ± (х^л) С х.

Дескриптор G : Y ^ Yл называем экстериоризатором в точке у Е Y, если отображение G^ : Yл ^ Y является проективным, у Е Dom G± и выполняется неравенство уЛ С G±(y).

Из свойства 7 вытекает справедливость следующего предложения.

Предложение 3. Если дескриптор F : X ^Л ^ X является интериоризатором в точке x Е X, то x Е Dom F ^т и

X (F ± (x ^{Л )} ^ x)) = X (x ^л ^ F ^T (x^ .

Если дескриптор G : Y ^ Y ^л является экстериоризатором в точке у Е Y, то у ^л Е Dom G ^ и

Y (у ^л ^ G ± (y) = Y G ^T (у ^л )) ^ у) .

• 4.5.    Дуальные дескрипторы. Пусть ( k, l) — дуальная пара вполне изотонных отображений k : X ^ Y и l : X ^ Y . Декартовы степени k ^л : Y ^л ^ X ^л и 1 ^л : Y ^л ^ X ^л отображений к и l соответственно являются вполне изотонными. Отображения (k ^л ) ± : Y ^л ^ X ^л , (k ^л ) ^т : X ^л ^ Y ^л , (1 ^л ) ± : Y ^л ^ X ^л и ( 1 ^л ) ^т : X ^л ^ Y ^л совпадают с декартовыми степенями отображений k ^∓ , k ^± , l ^∓ и l ^± соответственно, т. е.

(к ^л ) ± = (k ^т ) ^л , (k^ =(k ± ) ^л , (1 ^л ) ± ₌ (1 ^ ) ^л , (1 ^л ) Т =(k ± ) ^л .

Рассмотрим дуальные пары (к,1^л), (k\Q и ориентированные диаграммы

Y = Yл k               lΛ

X -— X X ^л

F

Yл ^-Y Y kΛ               l

Xл <—- X

F

Y -±^Y Yл к±              (/л)т

X-- X X ^л

F∓

Y^л G^.^ y

( к ^л ) т               l ±

Xл —^X

F±

Если дескриптор G : Y ^ Y ^л является дуальным к дескриптору F : X ^л ^ X относительно дуальной пары к к, 1^л^ и относительно дуальной пары <^ к ^л , l ^, то дескриптор G называем дуальным к дескриптору F . Согласно этому определению дескриптор G является дуальным к дескриптору F , если для любого x Е Dom F ^ и х л Е Dom F ± выполняются неравенства:

(l^ О F T (x) ^ G ± о k ± (x), l ± О F ± (x л ) ^ G ^T О (к ^л ) ^т (x л ).

Если дескриптор G : Y ^ Y ^л является дуальным к дескриптору F : X ^л ^ X и отображение G ± : Y ^ Y ^л является проективным, то по предложению 2 для любых x Е Dom F т и x л Е Dom F ± выполняются включения:

Y (k ± (x) <  у) С Dom G ± .

Далее рассмотрим дуальные пары (l, к ^Л ^, ll^, к} и ориентированные диаграммы

X -^-Fr X ^Л

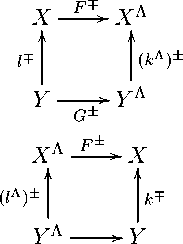
G ^∓

l               k ^Λ

Y - -- Y ^Л

G

XЛ TF~ X lΛ                k

Y ^Л ₌ V

G

Если дескриптор F : X ^Л ^ X является дуальным к дескриптору G : Y ^ Y ^Л относительно дуальной пары ^l, к^Л^ и относительно дуальной пары <^1^Л , к^, то дескриптор F называем дуальным к дескриптору G. Согласно этому определению дескриптор F является дуальным к дескриптору G, если для любых y Е Dom G ± и у л Е Dom G ^ выполняются неравенства

(к ^Л ) ± О G ± (у) С F ^т О 1 ^т (у), к О а ^ (у л ) С F ± о (1 ^Л ) ± (у л ).

Если дескриптор F является дуальным к дескриптору G и отображение F ± : X ^Л ^ X является инъективным, то по предложению 2 для любого у Е Dom G ± выполняется включение

X(Г (у) С x) С Dom F ' .                              (7)

Предложение 4. Если проективный дескриптор G : Y ^ Y ^Л является дуальным к дескриптору F : X ^Л ^ X и дескриптор F является интериоризатором в точке x Е Dom { k ± , l ' } , то дуальный дескриптор G является экстериоризатором в любой точке у Е Y, удовлетворяющей неравенствам k ± (x) С у С l ± (x) .

Если инъективный дескриптор F : X ^Л ^ X является дуальным к дескриптору G : Y ^ Y ^Л и дескриптор G является экстериоризатором в точке у Е Dom { k ^т , l ± } , то дуальный дескриптор F является интериоризатором в любой точке x Е X , удовлетворяющей неравенствам 1 ^т (у) С x С к ^т (у) .

• <1 Во-первых, пусть дескриптор F : X ^Л ^ X является интериоризатором в точке x Е Dom { k ± , 1 ^т } . Тогда x ^Л Е Dom F ± и F ± (x ^Л ) С х. По предложению 3 x Е Dom F ' и

• xЛ С FT(x).

Предположим, что дескриптор G является дуальным к дескриптору F , отображение GT : YЛ ^ Y является проективным и точка у Е Y удовлетворяет неравенствам k±(x) С у С l±(x). Отметим, что из неравенства у С lT(x) вытекает неравенство уЛ С (l±)Л(xЛ) = (lЛ)T(xЛ), а в силу (6) из неравенства k±(x) С у вытекает включение у Е Dom G±. При этом по определению дуального отображения для любого x Е Dom Fт выполняется неравенство

(1 ^Л ) ^т О F ^T (x) С G ± о k ± (x).

Следовательно,

ул С (^(Z) С (^)J ◦ FJ(x) С G± ◦ k±(x) С G±(y), т. е. ул С G±(y). Это означает, что дескриптор G является экстериоризатором в точке у.

Во-вторых, пусть дескриптор G : Y ^ Y ^л является экстериоризатором в точке у Е Dom { k ^J ,l ± } . Тогда у Е Dom G ± и выполняется неравенство

У ^Л С G ± (У).

Предположим, что дескриптор F : XЛ ^ X является дуальным к дескриптору G, отображение F± : XЛ ^ X является инъективным и точка x Е X удовлетворяет неравенствам lJ(y) С x С kJ(y). Отметим, что из неравенства x С kJ(y) вытекает неравенство хЛ С (кТ)Л(УЛ) = (кЛ)±(УЛ), а в силу (7) из неравенства lJ(y) С x вытекает включение x Е Dom FJ. При этом по определению дуального отображения для любого x С Dom G± выполняется неравенство

(к ^Л ) ± О G ± (y) С F ^J о l ^J (y).

Следовательно, xл С (кл)±(ул) С (кЛ)± о G±(xл) С FJ ◦ lJ (у) С FJ (x), т. е. xл С FJ(x). По предложению 1 xл Е Dom F± и F±(xл) С x. Это означает, что дескриптор F является интериоризатором в точке x. >

• 5.    Односторонняя схема двойственности

  • 5.1.    Инъективное и проективное описания. Пусть { Х д : А Е Л } и { У д : Л Е Л} — произвольные семейства частично упорядоченных множеств, X Λ и Y Λ — декартовы произведения этих семейств соответственно. Из множеств X, X λ , Y, Y λ и X ^Λ , X Λ , Y ^Λ , Y Λ сформируем простые ориентированные циклы:

X __^ y __+ Y _д „+ х _д __+ x,

Х _л --♦ Y _Л --♦ Y ^Л --♦ X ^Л --♦ Х _л .

Выберем произвольное семейство {mд : Л Е Л} вполне изотонных отображений mд : Хд ^ X. Считаем, что для любого Л Е Л отображение m± : Хд ^ X является проективными. Значит, для любого Л Е Л отображение mJ : X ^ Хд является инъективным. Символом mл : XЛ ^ Хл обозначим декартово произведение семейства {mд : Л Е Л}. Отображение т± := (тл)± : Xл ^ Хл совпадает с декартовым произведением семейства {mJ : Л Е Л} и является проективным, а отображение mJ := (тл)J : Хл ^ Xл совпадает с декартовым произведением семейства {т± : Л Е Л} и является инъективным. Если F : Xл ^ X — какой-либо интериоризатор в точке x Е X, то равенство

x = F ± о m J о т ± (x ^Л )

называем правилом инъективного описания . Если оно выполнено для какого-либо элемента x G X, то говорим, что элемент х допускает (инъективное) описание по правилу (8). По определению интериоризатора отображение F ± : X a ^ X является инъективным. Значит, если элемент х G X допускает описание по правилу (8), то он восстанавливается по множеству { m J о m ± (x) G X : A G Л } с помощью инъективного отображения F ^± .

Выберем другое семейство {пд : A G Л} вполне изотонных отображений пд : Y ^ Ya. Считаем, что для любого A G Л отображение п± : Y ^ Ya является инъективными. Значит, для любого A G Л отображение nJ : Ya ^ Y является проективным. Символом пл : YA ^ YД обозначим декартово произведение семейства {пд : A G Л}. Отображение п± := (пд)± : YA ^ YД совпадает с декартовым произведением семейства {nJ : A G Л} и является инъективным, а отображение nJ := (nA)J : YД ^ YA совпадает с декартовым произведением семейства {п± : A G Л} и является проективным. Если G : Y ^ Yд — какой-либо экстериоризатор в точке y G Y, то равенство y = GJ о п± о nJ(yA) (9)

называем правилом проективного описания . Если оно выполнено для какого-либо элемента y G Y, то говорим, что элемент y допускает (проективное) описание по правилу (9). По определению экстериоризатора отображение G ^J : У д ^ Y является проективным. Значит, если элемент y G Y допускает описание по правилу (9), то он восстанавливается по множеству { п ± о n J (y) G Y : A G Л } с помощью проективного отображения G ^J .

Предложение 5. Если вполне изотонное отображение m± : Xд ^ Xa является проективным, то для любого хд G Dom m± выполняется неравенство mJ о m±(xд) < хд-

Если вполне изотонное отображение n± : YA ^ Yд является инъективным, то для любого yA G Dom nAJ выполняется неравенство n± о nJ(yA) < УД-

• <1 Во-первых, предположим, что вполне изотонное отображение m ± : X ^д ^ X a является проективным. Условно обратное к отображению m ± : X ^д ^ X a совпадает с отображением (m ± ) ^- = m J : X a ^ X ^д и является инъективным. В свою очередь, условно обратное к отображению m J : X a ^ X ^A совпадает с отображением m ± : X ^A ^ X a . Значит, по свойству 1 вполне изотонных отображений для любого х д G Dom m ± выполняется неравенство m J о т ± (х д ) = m J о (m J ) ^- (х д ) <  х д .

• 5.2.    Дуальные описания. Пусть { h A : A G Л } — произвольное семейство вполне изотонных отображений h A : Y a ^ X a , h A : X a ^ YA — декартово произведение этого семейства. Рассмотрим дуальную пару h Λ , k ^Λ , ее зеркальную дуальную пару k ^Λ , h Λ

  и систему из четырех ориентированных диаграмм

  
  

  n ^±

  У _л — У ^л

  
  

  n Λ

  У_л <—^ У ^л

  
  
  

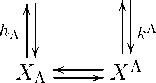
  h ±             ( k ^A ) ^T

  Хл — X ^{л m} Λ ^∓

  
  

  У ^л

  
  

  n _Λ ^∓

  
  

  У л

  
  

  n ^Λ

  ^Y ^ > ^Yл

  
  
  

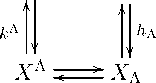
  ( к ^лУ           h ±

  X ^л —— Хл ^m Λ ^±

  
  

  Если вполне изотонное отображение п л является дуальным к отображению т л относительно дуальной пары ^л,к^л^> и относительно зеркальной дуальной пары (k ^л ,hл), то отображение п л называем дуальным к отображению т л . Отображение п л является дуальным к отображению т л , если для любых х л G Domm J С Х л и х л € Dom т ± С X ^л соответственно выполняются неравенства:

  (к ^л ) ^Т о т ^ (х л ) ^ п ± о h ± (х л ), h ± о т ± (х л ) ^ n J о (к ^л ) ^Т (х д ).         (10)

  Далее рассмотрим систему из четырех ориентированных диаграмм

  
  
  
  
  

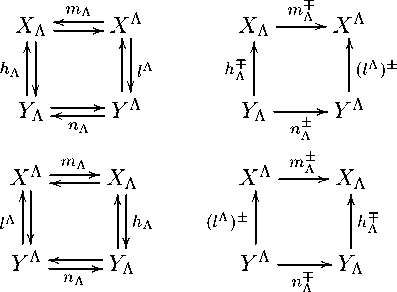
• 5.3.    Односторонняя схема двойственности. Рассмотрим ориентированные диа-

• граммы

Во-вторых, предположим, что вполне изотонное отображение n ± : Y A ^ Y ^A является инъективным. Условно обратное к отображению n ± : Y A ^ Y ^A совпадает с отображением (n ± ) ^- = n J : Y ^A ^ Y A и является проективным. В свою очередь, условно обратное к отображению n J : Y ^A ^ Y A совпадает с отображением n ± : Y A ^ Y ^д . Значит, по свойству 2 вполне изотонных отображений для любого у д G Dom n J выполняется неравенство ⁿ ± ^{о n J (}y A ) = ^{( n J )} - ^{о n J (}y A ) <  У Д . >

полученных с помощью горизонтальной симметрии и замены отображения кл отображением 1л. Если вполне изотонное отображение тл является дуальным к отображению пл относительно дуальной пары J hл, 1л ^ и относительно зеркальной дуальной пара (lA, ^л J то отображение тл называем дуальным к отображению пл . Отображение тл является дуальным к отображению пл, если для любых ул G DomnJ С Ул и ул G Domп± С Уд соответственно выполняются неравенства hJ о пл(Ул) < т± о (1л)±(ул), (1л)± о п±(Ул) < mJ о hл(УЛ). (11)

Если дескриптор F : X ^л ^ X является дуальным к дескриптору G : X ^ X ^л и отображение т л : X ^л ^ X л является дуальным к отображению п л : У л ^ У ^л , то правило описания (8) называем дуальным к правилу (9). С другой стороны, если дескриптор G : X ^ X ^л является дуальным к дескриптору F : X ^л ^ X и отображение п л : У л ^ У ^л является дуальным к отображению т л : X ^л ^ X л , то правило описания (9) называем дуальным к правилу (8).

Y G YΛ k               lΛ

X X ^Λ F

X F XΛ l               kΛ

Y Y ^Λ

G

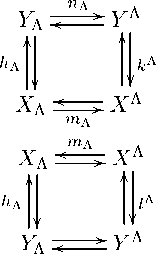
где F , G — дескрипторы; m Λ , n Λ , h Λ — декартовы произведения семейств вполне изо-тонных отображений; k ^Λ — декартова степень вполне изотонного отображения k; l ^Λ — декартова степень вполне изотонного отображения l. Справедлива следующая теорема.

Теорема 1 (односторонняя схема двойственности) . Если элемент x Е Dom { k ± ,1 ± } допускает инъективное описание по правилу (8) , то любой элемент у Е Y, удовлетворяющий неравенствам k ± (x) С у С 1 ± (x) , допускает проективное описание по дуальному правилу (9) .

Если элемент у Е Dom { k ' ,1 ' } допускает проективное описание по правилу (9) , то любой элемент x Е X, удовлетворяющий неравенствам 1 ' (у) С x С к ' (у) , допускает инъективное описание по дуальному правилу (8) .

• <1 Во-первых, пусть дескриптор G : Y ^ Y ^л является дуальным по отношению к дескриптору F : X ^Л ^ X и элемент x Е Dom { k ± , 1 ± } допускает инъективное описание по правилу (8). Тогда дескриптор F является интериоризатором в точке x и

• x = F± о m' о m±(xA). (12)

Предположим, что вполне изотонное отображение пл : YA ^ YЛ является дуальным к вполне изотонному отображению mA : XЛ ^ Xa. Тогда в силу (10) для любого xa Е Dom m± выполняется неравенство h± о m±(xA) С п' ◦ (kA)'(xa). В силу (12) xA Е Dom m±, значит, h± о m±(xA) С п' о (kA)'(xA). (13)

Кроме того, в силу (10) для любых x a Е Dom m ' выполняется неравенство (k ^A ) ' о m ' (x A ) С п ± о h ± ( x a ) . При этом в силу (1) выполняются включения m ± (x ^A ) Е Im т ± С Dom m ' , значит,

(k ^A ) ' о m ' о m ± (x ^A ) С п ± о h ± о m ± (x ^A ). (14)

По предложению 4 дескриптор G является экстериоризатором в любой точке у Е Dom{k±,1±}, удовлетворяющей неравенствам k±(x) С у С 1±(x). Выберем произвольный элемент у Е Dom{k±, 1±}, удовлетворяющий этим неравенствам и отметим, что из неравенства k±(x) С у вытекает неравенство (kA)'(xA) С уЛ. По определению дуального отображения для любого xa Е Dom F± выполняется неравенство 1± о F±(xA) С G' о (kA)'(xA). Из равенства (12) следует, что m' о m±(xA) Е DomF±, значит, в силу (12), (14) и (13) имеем у С 1±(x) = 1± о F± о m' о m±(xA)

С G ' о (k ^A ) ' о m ' о m ± (x ^A ) С G ' о п ± о h ± о m ± (x ^A ) С G ' о п ± о п ' о (k ^A ) ' (x ^A ) С G ' о п ± о п ' (у ^Л ),

• т. е. y С G ^J о п ± о n J (y ^Л ). Но по предложению 4 дескриптор G является экстериоризато-ром в точке y , значит, по определению экстериоризатора и по предложению 5 выполняются неравенства G ^J о п ± о n J (y ^Л ) С G ± (y ^Л ) С у. Следовательно, G ^J о п ± о n J (y ^Л ) = у, т. е. элемент y допускает проективное описание по дуальному правилу (9).

Во-вторых, пусть дескриптор F : XЛ ^ X является дуальным по отношению к дескриптору G : Y ^ YЛ и элемент у Е Dom{kJ,lJ} допускает проективное описание по правилу (9). Тогда дескриптор G является экстериоризатором в точке y и у = GJ о п± о nJ(yЛ).

Предположим, что вполне изотонное отображение mл : XЛ ^ Xл является дуальным к вполне изотонному отображению пл : Yл ^ YЛ. Тогда в силу (11) для любого ул Е Domп± выполняется неравенство hJ оnJ(yл) С т±о (1Л)±(ул). В силу (15) ул Е DomnJ, значит, hl о пл(ул) С т± о (1л)±(ул)•

Кроме того, в силу (11) для любых у л Е Dom п ± выполняется неравенство (1 ^Л ) ± о п ± (у л ) С m J о h J (y л ). При этом в силу (1) выполняются включения П д (у ^Л ) Е Im n J С Dom п ± , значит,

(1 ^Л ) ± о п ± о n ^J (y ^Л ) С m ^J о h ^J о n ^J (y ^Л ).

По предложению 4 дескриптор F является интериоризатором в любой точке x Е Dom{kJ, lJ}, удовлетворяющей неравенствам lJ(y) С x С kJ(y). Выберем произвольный элемент x Е Dom{kJ,lJ}, удовлетворяющий этим неравенствам и отметим, что из неравенства lJ(y) С x вытекает неравенство (1Л)±(уЛ) С xЛ. По определению дуального отображения для любого ул Е DomGJ выполняется неравенство kJоGJ(ул) С F±о(1Л)±(ул). Из равенства (15) следует, что п± о nJ(yЛ) Е DomGJ, значит, в силу (15), (17) и (16) имеем x С kJ(y) = kJ о GJ о п± о nJ (уЛ)

С F ± о (1 ^Л ) ± о п ± о n J (у ^Л ) С F ± о m J о h J о n J (y ^Л ) С F ± о m J о т ± о (1 ^Л ) ± (у ^Л ) С F ± о m J о m ± (x ^Л ),

• т. е. x С F ± о m J о m ± (x ^Л ). Но по предложению 4 дескриптор F является интериоризато-ром в точке x, значит, по определению интериоризатора и по предложению 5 выполняются неравенства F ± о m J о m ± (x ^Л ) С F ± (x ^Л ) С x. Следовательно, F ± о m J о m ± (x ^Л ) = x, т. е. элемент x допускает инъективное описание по дуальному правилу (8). >

• 6. Двусторонняя схема двойственности

• 6.1.    Принцип двойственности. Пусть X, Y — частично упорядоченные множества, к : X ^ Y — инъективное отображение, к - : Y ^ X — условно обратное отображение. По свойству 6 отображение k ^- является проективным. Символом X 0 обозначим полный образ Im к - , а символом Y Q обозначим полный образ Im к.

В исследовательской практике, как правило, двойственные переходы осуществляются по упрощенной схеме. Будем называть ее двусторонней схемой двойственности. Упрощение достигается путем отождествления вполне изотонных отображений k : X ^ Y и l : X ^ Y. При переходе к упрощенной схеме число рассматриваемых параллельно ситуаций резко сокращается и введенное нами обозначение k : X ^ Y теряет актуальность. В этих ситуациях вполне достаточно стандартное обозначение k : X ^ Y. При этом частично упорядоченные множества X и Y выбираются произвольно, значит, можно считать, что вполне изотонное отображение k : X ^ Y является инъективным. В противном случае можно пару (X, Y) заменить парой (Y, X), а отображение k : X ^ Y заменить условно обратным отображением k- : Y ^ X. Таким образом, двусторонняя схема двойственности предполагает лишь две зеркальные ситуации, которые легко сводятся одна к другой. Это позволяет исследовать лишь одну из этих ситуаций.

Предложение 6 (принцип двойственности) . Между элементами x Е X q и y Е Y 0 можно установить взаимно однозначное соответствие по правилу:

y = k(x), x = к - (y).

• <1 Во-первых, убедимся, что образ ^Xq ) совпадает с Y Q . Действительно, ^Xq ) С k(X ) = Im к = : Y Q . С другой стороны, если у Е Y q , то по свойству 4 у = к о к - (y) = k(x), где x := k ^- (y) Е X q , значит, y Е к(Х о ), т. е. Y q С ^X q ) . Следовательно, к(Х о ) = Y Q . Во-вторых, убедимся, что образ к ^- (Y 0 ) совпадает с X q . Действительно, к ^- (Y Q ) С k ^- (Y ) = Im к ^- = : X q . С другой стороны, если x Е X q , то по свойству 4 x = к ^- о k(x) = к ^- (y), где y := k(x) Е Y q , значит, x Е к ^- (Y 0 ), т. е. X q С к ^- (Y 0 ). Следовательно, к ^- (Y 0 ) = X q . Таким образом, из свойства 4 вытекает, что сужение отображения k ^- на образ Y 0 и сужение отображения к на образ X q являются взаимно обратными отображениями. >

• 6.2.    Дуальные дескрипторы. Пусть Л — множество и 0 Е Л; X ^Л , Y ^л — декартовы степени частично упорядоченных множеств X и Y соответственно; к ^Л : X ^л ^ Y ^л — декартова степень отображения к : X ^ Y . Отображение к ^л является проективным. Его условно обратное отображение (к ^Л ) ^- : Y ^л ^ X ^л совпадает с декартовой степенью условно обратного отображения к ^- : Y ^ X и является инъективным. Рассмотрим диаграммы, в ориентировании которых нет необходимости

  Y

  
  

  G

  
  

  Y ^Λ

  
  

  Y ^Λ

  
  

  G ^-

  
  

  Y

  
  

  k

  X

  
  

  k ^Λ

  
  

  k ^Λ

  
  

  F ^-

  
  

  X

  
  

  Λ

  
  

  Λ

  
  

  k

  X

  
  

  X F

  k ^-

  Y Y ^Λ

  G

  
  

  XΛ

  (kΛ)-

  Y ^Λ Y

  G ^-

  
  

Символом к о обозначим отображение X q н- Y q | x н- k(x), а символом к — обозначим отображение Y q н- X q | y н- k ^- (y). Из доказанного принципа двойственности следует, что отображение k 0 является порядковым изоморфизмом X 0 на Y 0 , а отображение k ₀ ^- совпадает с обратным отображением и является порядковым изоморфизмом Y 0 на X 0 . Отображения k 0 и k ₀ ^- являются инъективными и проективными одновременно, и условно обратное отображение (к о ) ^- совпадает с отображением к - , а условно обратное отображение (к - ) ^- совпадает с отображением к о .

Дескриптор G : Y ^ Y ^Л является дуальным к дескриптору F : X ^Л ^ X, если согласно определению для любого x Е Dom F ^- и x л Е Dom F соответственно выполняются неравенства:

к ^л о F (x) Е G о k(x), к о F (x л ) Е G о k ^л (x л ).

Дескриптор F : X ^л ^ X является дуальным к дескриптору G : Y ^ Y ^Л , если для любых y Е Dom G и у л Е Dom G - соответственно выполняются неравенства:

(к ^л ) ^- О G(y) ^ F ^- о к ^- (у), к - о G^-^) ^ F о (к ^л ) ^- (у л ).

Из предложения 4 вытекает справедливость следующего предложения.

Предложение 7. Если проективный дескриптор G : Y ^ Y ^л является дуальным к дескриптору F : X ^л ^ X и дескриптор F является интериоризатором в точке x Е X -, то дуальный дескриптор G является экстериоризатором в точке у = k(x) Е Y Q.

Если инъективный дескриптор F : X ^л ^ X является дуальным к дескриптору G : Y ^ Y ^л и дескриптор G является экстериоризатором в точке у Е Y - , то дуальный дескриптор F является интериоризатором в точке x = к - (у) Е X -.

• 6.3.    Взаимно дуальные дескрипторы. Пусть X ₀ ^Λ , Y ₀ ^Λ — декартовы степени частично упорядоченных множеств X o и Y - соответственно; к ^л : X -^ ^ Y^ — декартова степень отображения к - : X o ^ Y - . Отображение к ^л является порядковым изоморизмом X ₀ ^Λ на Y ₀ ^Λ и является инъективным отображением и проективным отображением одновременно. Его условно обратное отображение (к -^ ) ^- : Y) ,' ^ X -^ совпадает с обратным отображением и является порядковым изоморфизмом Y ₀ ^Λ на X ₀ ^Λ . Рассмотрим диаграм-

• мы

Y 0   ^{G 0} Y 0 ^Λ

-Λ k0

X0

F0-

X0  F0 X0Λ k0-

Y 0 Y ^Λ

G0-

где F - : X -^ ^ X o — инъективный дескриптор, G o : Y - ^ Y^ — проективный дескриптор. Дескрипторы F 0 и G 0 называем взаимно дуальными , если

G o = к Л о F o ^- о к ^- ,  F o = k o о G o о к Л .

Предложение 8. Если дескрипторы F 0 и G 0 являются взаимно дуальными, то дескриптор F 0 является дуальным к дескриптору G 0 , а дескриптор G 0 является дуальным к дескриптору F 0 .

• <1 Предположим, что дескрипторы F o : X q ^ X o и G o : Y - ^ Y Q ^A являются взаимно дуальными. Отображения k ₀ ^- , G ₀ ^- , k ₀ ^Λ являются инъективными, значит, по свойству 10 вполне изотонных отображений условно обратное отображение F ₀ ^- представляется в виде композиции (к-¹) ^- о G - о к - . Отображения к-¹, F — , к — являются проективными, значит, по свойству 10 условно обратное отображение G ^- представляется в виде композиции к - о F - о (к ^Л ) ^- . При этом для любого x Е Dom F — имеем

ко о F0 (x) = кЛ о (кЛ)- о G- о к-(x) = G- о к-(x), а для любого xл Е Dom F- имеем к- о F-(xл) = к- о к0 о G- о к^л) = G- о к^л).

Значит, дескриптор F является дуальным к дескриптору G . С другой стороны, для любого у Е Dom G имеем

Λ -             Λ - Λ -   -       -   -

(к ) о G (у) = (к ) о к о F о к (у) = F о к (у), а для любого ул Е Dom Go имеем к- о Go (ул) = ко о ко о Fq о (кд)-(уд) = Fq о (кл)-(уд).

Значит, дескриптор G 0 является дуальным к дескриптору F 0 . ⊲

Существует простой способ построения пар (F o , G o ) взаимно дуальных дескрипторов. Он описан в следующем предложении.

Предложение 9. Если дескриптор F o : X ^Q ^ X q является инъективным и дескриптор G o : Y q ^ Y Q ^Q совпадает с композицией к ^д о F Q о к - , то дескрипторы F q и G q являются взаимно дуальными.

Если дескриптор G o : Y Q ^ Y Q^q является проективным и дескриптор F q : X ^Q ^ X q совпадает с композицией к - о G - о к ^д , то дескрипторы F q и G q являются взаимно дуальными.

• <1 Во-первых, предположим, что дескриптор F q : X ^Q ^ X q является инъективным и дескриптор G q : Y q ^ Y Q^q совпадает с композицией к ^д о F Q о к ^- . По свойству 10 дескриптор G 0 является проективным и его условно обратное отображение G ^- представляется в виде композиции к у о F q о (ку') ^- . Значит,

• 6.4.    Взаимно дуальные описания. Выберем произвольное семейство { т д : А Е Л } проективных отображений т д : X д ^ X q . Символом т д : X q ^ X ^Д обозначим декартово произведение семейства { т д : А Е Л } . Отображение т л является инъективным. Если F q : X ^д ^ X q — какой-либо интериоризатор в точке x Е X q , то правило инъективного описания имеет следующий вид:

к0- о G- о к л = к0- о к о F о (к л)- о к л = F , а это означает, что дескрипторы F и G являются взаимно дуальными. Во-вторых, предположим, что дескриптор Gq : Yq ^ YQд является проективным и дескриптор Fq : Xд ^ Xq совпадает с композицией к— о G— о кд. По свойству 10 дескриптор Fq является инъективным и его условно обратное отображение F - представляется в виде композиции (кд)- о Gq о ку. Значит, к л о F0- о к0- = к л о (к л)- о G о к о к0- = G , а это означает, что дескрипторы F и G являются взаимно дуальными. ⊲

Из предложений 7 и 8 вытекает справедливость следующего предложения.

Предложение 10. Если дескрипторы F и G являются взаимно дуальными, то дескриптор F q является интериоризатором в точке x Е X q тогда и только тогда, когда дескриптор G q является экстериоризатором в точке у = к(х) Е Y q .

x = F q о т л о т - (х ^л ).                             (18)

Выберем семейство { п д : А Е Л } инъективных отображений п д : Y q ^ У д . Символом п л : Y q ^д ^ У д обозначим декартово произведение семейства { п д : А Е Л } . Отображение п л является проективным. Если G q : Y q ^ Y Q ^д — какой-либо экстериоризатор в точке у Е Y q , то правило проективного описания имеет следующий вид:

у = G - о п - о п д (у ^д ).                                (19)

Пусть { h \ : А € Л } — произвольное семейство порядковых изоморфизмов h \ : Y \ ^ X \ , h л : У л ^ Х л — декартово произведение этого семейства. Отображение h л является порядковым изоморфизмом, значит, оно является инъективным отображением и проективным отображением одновременно. Рассмотрим систему из двух диаграмм:

Y Λ	n Λ -	Λ Y 0	Λ Y 0	n Λ	Y Λ
h Λ -		Λ k 0	Λ k 0		h Λ -
X Λ	m Λ	Λ X 0	Λ X 0	m Λ -	X Λ
Λ X 0	m Λ -	X Λ	X Λ	m Λ	X0 Λ
( k 0 Λ ) -		h Λ	h Λ		( k 0Λ ) -
Λ Y 0	n Λ	Y Λ	Y Λ	n Λ	Y 0 Λ

Согласно определению отображение nΛ является дуальным к отображению mΛ, если для любых хл € Dom тл С Хл и хл € Dom т— С Х,) соответственно выполняются неравенства кО ° тл(хл) < п- ° h— (хл), h- ° тл(хл) < пл ° k-(xл)•

Отображение тл является дуальным к отображению пл, если для любых ул € Dom пл С УОл и Ул € Dom п— С Уд соответственно выполняются неравенства hл ° пл(ул) ^ т— ° (k-)-(yл), (к,) । ° п-(ул) ^ тл ° h-(y-).

Говорим, что вполне изотонные отображения nΛ и mΛ являются взаимно дуальными, если пл = h— ° т— ° (к^, тл = (к^- ° п- ° h—.

Если дескрипторы F : Х, ) ^ Х о и G o : Х о ^ Х, ) являются взаимно дуальными и вполне изотонные отображения т л : Х л ^ Х, ) и п л : У 0 ^л ^ Уд являются взаимно дуальными, то правила описания (18) и (19) называем взаимно дуальными .

Предложение 11. Если вполне изотонные отображения т л : Х л ^ Х у и п л : У 0 ^л ^ У л являются взаимно дуальными, то отображение т л является дуальным к отображению n Λ и отображение n Λ является дуальным к отображению m Λ .

• <1 Предположим, что вполне изотонные отображения т л : Х л ^ Х у и п л : У 0 ^л ^ У л являются взаимно дуальными. По свойству 11 вполне изотонных отображений условно обратные отображения представляются в виде следующих композиций:

п ^— = к о ° т л ° h л , т ^— = h л ° п л ° к О) .

Значит, для любого х л € Dom т л и х л € Dom т ^— соответственно выполняются равенства

^ ° т л (х л ) = к ^л ° (k^-') ^- ° п ^— ° h _л (x л ) = п _л ° h _л (x л ), h ^— ° т _л (х л ) = h ^— ° h л ° п л ° k ^- (x л ) = п л ° k ^- (x л ).

Следовательно, отображение nΛ является дуальным к отображению mΛ . С другой стороны, для любых ул € Dom пл С УОл и ул € Dom пл— С Ул соответственно выполняются равенства h— ° п—(ул) = h— ° кл ° тл ° hл(yл) = тл ° кл(ул), кЛ ° пл(ул) = кЛ ° hл ° тК ° (кЛ) (ул) = тл ° hл(yл).

Значит, отображение m Λ является дуальным к отображению n Λ . ⊲

Из предложения 11 вытекает справедливость следующего предложения.

Предложение 12. Если правила описания (18) и (19) являются взаимно дуальными, то правило (18) является дуальным к правилу (19) , а правило (19) является дуальным к правилу (18) .

• 6.5.    Двусторонняя схема двойственности. Из предложений 10, 12 и теоремы 1 вытекает следующая теорема.

Теорема 2 (двусторонняя схема двойственности) . Если правила описания (18) и (19) являются взаимно дуальными, то элемент x G X q допускает инъективное описание по правилу (18) тогда и только тогда, когда элемент у = k(x) G Y Q допускает проективное описание по правилу (19) .

Теорема 2 (двусторонняя схема двойственности) обобщает «схему двойственности» из статьи [1] и теорему 1 из статьи [4]. Аналогичные теоремы есть и в статье [2] и в монографии [3] (многомерная ситуация). Эти теоремы являются основой для решения задач спектрального синтеза в комплексной плоскости. Они позволяют свести задачу спектрального синтеза к двойственной задаче локального описания. Теорема 2 придает теоремам двойственности общий вид и может быть использована при решении других задач. Однако, эти задачи должны относиться к рефлексивному случаю (т. е. задача должна быть сформулирована в условиях рефлексивного локально выпуклого пространства). Доказанная выше теорема 1 (односторонняя схема двойственности) допускает ее использование при решении задач в условиях нерефлексивного локально выпуклого пространства. Конкретного опыта в этом направлении в открытой печати пока нет.