Однозначная разрешимость задачи об ударе с отрывом твердого тела о неоднородную жидкость

В этой статье изложена постановка задачи об ударе твердого тела о неоднородную несжимаемую жидкость. Рассмотрены случаи удара без отрыва и с отрывом. Доказана однозначная разрешимость соответствующих смешанных краевых задач в случае ограниченной области.

В § 1 изложена постановка краевых задач и показано, что на неподвижной твердой поверхности отрыв невозможен.

В § 2 приведены с доказательством некоторые известные результаты теории вариационных неравенств в той форме, в которой они используются в работе.

В § 3 доказаны существование и единственность решения задачи в случае безотрывного удара.

В § 4 изложена постановка задачи об ударе с отрывом. Для этой нелинейной краевой задачи доказаны существование и единственность решения.

• § 1.    Постановка задачи о гидродинамическом ударе

Рассматривается задача о течении жидкости, вызванном ударом по плавающему в ней твердому телу. Предположим, что жидкость заполняет ограниченную область D в R ³ (см. рис. 1).

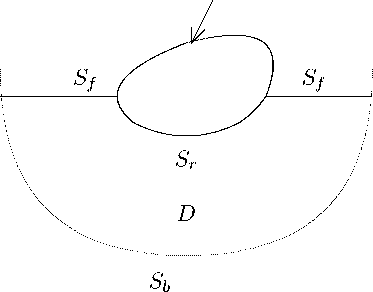
Рис. 1.

Граница ∂D области D состоит из поверхности S b (дно контейнера), свободной поверхности S f и смоченной поверхности твердого тела S r , так что dD = S b U S r U S f ; множества S b , S r , S f считаем замкнутыми. Обычно в приложениях S f — плоская поверхность, но для дальнейшего это предположение не нужно. Характерно, что даже в случае, когда S b , S r и S f — гладкие поверхности, граница ∂D является лишь кусочногладкой с особенностями типа двугранного угла в точках пересечения S f ∩ S b и S f ∩ S _r свободной границы с дном и соответственно с поверхностью твердого тела. Возможны, конечно, и особенности самих поверхностей S b и S _r . Будем их считать кусочно гладкими. Дальше, говоря о граничных условиях, будем подразумевать, что они выполняются в регулярных точках поверхностей, причем выполнены также соответствующие условия непрерывности вплоть до границы.

Предположим, что задана плотность жидкости p(x) при х G D, причем p — гладкая функция, которая всюду положительна: выполняется неравенство p(x) > po > 0 при всех x ∈ D с известной постоянной ρ 0. Как показано в [1], плотность жидкости не успевает измениться в ходе удара, так что ρ — известная функция, плотность жидкости до удара.

Предполагается, что в результате удара твердое тело мгновенно приходит в движение, приобретая скорость

V = U + ш Л х. (1)

Здесь U — поступательная, а ω — угловая скорости движения. На самом деле вектор U и псевдовектор ω заранее неизвестны. Однако на первом шаге решения задачи они считаются известными и определяются после того, как решена задача о движении жидкости после удара, по заданному ударному импульсу, подействовавшему на тело.

Как показано в [1], течение жидкости после удара ρ-потенциально, его поле скорости есть u = — grad у.                             (2)

Правая часть здесь — градиент в ρ-метрике ρds2 , где ds2 — евклидова метрика. Функция ϕ — потенциал течения, который имеет физический смысл импульсивного давления. Замечу, что в случае постоянной плотности задача об ударе была сформулирована классиками еще в XIX веке [2–4]. Случай же неоднородной жидкости, как ни странно, разобран в [1], по-видимому, впервые. Условие несжимаемости приводит к уравнению div

^ - grad у

)

= 0.

Левая часть здесь есть лапласиан А р , отвечающий --метрике.

Если предположить, что в результате удара жидкость не отрывается от твердых границ, то для определения потенциала ϕ получается смешанная краевая задача с граничными условиями у = 0,                                          (4)

S f

∂ϕ ∂n

-dn

= 0,

S b

- V _n .

S r

Условие (4) означает, что свободная граница не подвергается ударным воздействиям. Условие (5) следует из непроницаемости дна для жидкости; ^П = grad у • n, где n — единичный вектор нормали. Наконец, условие (6) требует, чтобы на смоченной границе твердого тела нормальные скорости жидкой частицы и примыкающей к ней точки границы S r совпадали; при этом V n = V • n. Конечно, это означает, что и граница твердого тела S r для жидкости непроницаема.

Решение линейной краевой задачи (3)–(6) о безотрывном ударе имеет, однако, аде к ватный физический смысл лишь при дополнительном условии: у(х) > 0 при всех x G D. Дело в том, что жидкость не может противостоять растяжению, которое имело бы место при отрицательном импульсивном давлении ϕ. Вместе с тем непроницаемость твердых границ есть лишь односторонняя связь: жидкость не может проникнуть внутрь твердого тела, но вполне может от него оторваться. В результате граничные условия на твердых поверхностях S _b и S _r приходится изменить и перейти к новой постановке задачи.

Задача об ударе с отрывом. Начнем с условия на неподвижной твердой границе S b . В каждой ее точке x либо у(х) > 0 и ^n (x) = 0, либо у(х) = 0, dn (x) > 0. Оказывается, однако, что второй случай, отвечающий отрыву, невозможен. Справедливо следующее утверждение.

Предложение 1. На неподвижной твердой стенке отрыв невозможен.

<1 Допустим, что в некоторой точке xo G S b отрыв происходит, так что y(xo) = 0, и компонента скорости жидкости вдоль внутренней нормали положительна:

∂ϕ ∂n

> 0.

Тогда это строгое неравенство остается верным и в некоторой окрестности точки xg на S b . Однако из него последовало бы, что y(x) <  0 в точках области D близких к xg (n — внешняя нормаль!). Таким образом, неравенство (7) несовместимо с требованием неотрицательности потенциала у. Итак, отрыв невозможен, и предложение доказано. B

Таким образом, условие (5) на S b сохраняет прежнюю форму и в задаче об отрывном ударе.

Краевое условие на подвижной твердой поверхности S r теперь формулируется следующим образом. Функция у на S r неотрицательна: y(x) > 0 для всех x G S r , и если y(x) > 0 в точке x G S r , то в этой точке р!^ = — V n . В итоге поверхность S r разделяется на части S ^g и S=, на которых (всюду, за исключением точек пересечения S ^g П S= — множества двумерной меры нуль) соответственно выполнены условия

у	= 0, S 0	1 ду ρ ∂n	+ V n	S 0	> 0,	(8)
1 ду и п + V n ρ ∂n		= 0, S =	у	S =	> 0.	(9)

Часть S ^g поверхности S r назовем зоной отрыва, а часть S= — безотрывной зоной.

Из строгого принципа максимума-минимума для эллиптического уравнения (3) следует, что условие неотрицательности на границе (y(x) > 0 при x G dD), влечет строгую положительность внутри области: y(x) > 0 при x G D. Поэтому кавитация, т. е. «внутренний отрыв» с образованием пузырей, невозможна уже в силу принятых краевых условий. Отсюда следует, что уравнение (3) также сохраняет силу.

Теперь мы можем сформулировать постановку задачи об ударе с отрывом. Требуется найти ρ-гармоническую функцию ϕ — решение уравнения

А р у = 0,

непрерывную вплоть до границы ∂D, удовлетворяющую прежним условиям на свободной границе S f и на дне S b :

у   =0,                                   (11)

S f

∂ϕ ∂n

= 0.

S b

Кроме того, функция у должна быть неотрицательной (у (x) > 0 при x G D) и удовлетворять краевым условиям (8), (9) на S r .

Поскольку зона отрыва S _r ^g заранее неизвестна, сформулированная задача нелинейна. Даже в случае однородной жидкости и двумерной области D она решена лишь в отдельных частных случаях. Л. И. Седов [4] поставил задачу об ударе с отрывом в двумерном случае и нашел решение в случае горизонтального удара по отрезку, погруженному в жидкую полуплоскость, при помощи виртуозного применения методов теории функций комплексного переменного. Ссылки на последующие работы по двумерной задаче об отрывном ударе Н. А. Кудрявцевой, В. С. Корчагина, М. В. Норкина можно найти в работе [1]. В трехмерном случае, вместо отдельных точек, разделяющих зоны отрывного и безотрывного удара, неизвестными оказываются разделяющие эти зоны кривые. Задача сразу из скалярной превращается в бесконечномерную. Возникающие трудности до сих пор не преодолены ни в одном конкретном случае.

• § 2.    Лемма о проекторе. Вариационное неравенство

Здесь в целях замкнутости изложения я привожу с доказательствами известные результаты о проекторе на выпуклое множество и вариационных неравенствах [5–8].

Лемма 1 (о проекторе). Пусть K — выпуклое замкнутое множество в гильбертовом пространстве H . Тогда для любой точки x ∈ H существует, и притом единственная, точка y ∈ K такая, что p(x,K) = kx - y\\.                                  (13)

Тем самым определен проектор Pk : H ^ K пространства H на выпуклое множество K :

У = Pk x.                                 (14)

C Положим inf \x — y\ = d, так что d = p(x, K). В частности, d = 0 и y = x в том и y∈K только том случае, когда x ∈ K .

Пусть {yn}, yn E K, n = 1, 2,... — минимизирующая последовательность. Докажем, что она сходится. Согласно равенству параллелограмма, имеем ym + yn x-

+

y _m - y _n

= 2 ( k x - У т ^ ⁺ k x - У п^ ) .

Поскольку k x - y _n k ² → d ² и

k x - y _m k ² → d ² при n, m → ∞ , то из (15) следует неравенство

lim m,n→∞

x -

y m ⁺ y n 2

6 d ² .

y _m + y _n

С другой стороны, ---2---

∈ K , ввиду выпуклости, а согласно определению величины

d, этот верхний предел больше либо равен d ² . Таким образом,

ющая последовательность:

(y m + y n )

---2--минимизиру-

lim m,n→∞

y _m + y _n x -

= d.

Теперь из (15) следует, что \ym — yn\ ^ 0 при m, n ^ го. Поскольку H полно, существует предел lim yn = у, а так как множество K замкнуто, y E K. При этом, очевидно, n→∞ kx — yk = d.

В предыдущем доказательстве существования фактически устанавливается и единственность. Более формально, если у и у — минимальные элементы, так что \ x — у \ = ||x — y \ = d, то последовательность y, y, y, y, ... — минимизирующая. По доказанному, она сходится. Поэтому y = y. B

Нелишне подчеркнуть, что в этой лемме не требуется, чтобы множество K было ограниченным. Дальше лемма применяется в случае, когда K — конус.

Вариационное неравенство. Пусть x E H и y = Pkx. Если u E K, то, ввиду выпуклости множества K , оно содержит и весь отрезок, соединяющий точки y и u. Это означает, что y + t(u — y) E K для любого t E [0,1]. Из (13) следует неравенство kx — y\2 6 kx — у — t(u — y)k2.

Его можно переписать в виде

2t(x - y,u - y) 6 t2ku - yk2.(19)

Разделив на t и устремив t к нулю, придем к неравенству

(x - y,u - y) 6 0(20)

для любого u ∈ K.

Очевидно, что и обратно, из неравенства (20) следует (18). Положив в нем t = 1, можем написать kx - yk2 6 kx - uk2.(21)

Из предыдущей леммы следует, что равенство в (21) может достигаться только при u = y = Pk x. Мы пришли к следующей характеризации проектора Р к .

Лемма 2 (о решении вариационного неравенства) . Пусть x ∈ H , и K — выпуклое замкнутое множество в H . Тогда существует и притом единственный элемент y , удовле творяющий неравенству (20) при любом u G K. При этом y = Р к x.

Понятие проектора на выпуклое замкнутое множество K является естественным обобщением проектора на (линейное) подпространство L в H. В этом случае неравенство (20) можно заменить равенством, а вместо u - y написать произвольный элемент v ∈ L.

Заметим еще, что оператор PK непрерывен, более того, липшицев, и, еще более того — нерастягивающий: справедливо следующее утверждение.

Лемма 3. Для любых x0 и x00 ∈ H выполняется неравенство kPKx - Ркx0k 6 kx0 - x00k.(22)

C Положим y' = Ркx', y00 = Ркx00 и x0 = y' + v0, x00 = y00 + v00. Имеем kx0 - x00k2 = W - y" k 2 + kv0 - v"k2 + 2(y0 - y", v0) + 2(y" - y0, v").(23)

Последние два слагаемых неотрицательны. Действительно, полагая в вариационном неравенстве (20) сначала x = x ⁰ , y = y ⁰ , u = y" , а затем x = x ⁰⁰ , y = y", u = y ⁰ , найдем

(v0,y00 - y0) 6 0, (v00,y0 - y00) 6 0.(24)

Поэтому из (23) следует неравенство kx0 - x00k2 > ky0 - y"k2 + kv0 - v00k2,(25)

которое влечет неравенство (22). B

• § 3.    Вариационный принцип в задаче о безотрывном ударе

Сначала рассмотрим вариационный принцип в задаче о безотрывном ударе. Это означает, что мы отбрасываем условие положительности потенциала ϕ и рассматриваем классическую смешанную задачу теории потенциала. Собственно говоря, если окажется, что для решения этой задачи ^(x) > 0 в D, то больше ничего и не нужно — удар происходит без отрыва. Например, если удар наносится по лежащему на поверхности диску, то он происходит без отрыва, когда точка приложения вертикального импульса находится в круге с тем же центром, радиуса ¹ ₅ радиуса диска. Аналогичный результат, с тем

Однозначная разрешимость задачи об ударе с отрывом твердого тела 3–85 же коэффициентом ¹ ₅ , справедлив и в случае эллипсоида, погруженного наполовину в жидкое полупространство [9]. Во многих работах найдены условия безотрывности удара в случае однородной жидкости. Когда оказывается, что потенциал ϕ, в предположении отсутствия отрыва, меняет знак в области течения, то это и есть сигнал о необходимости перехода к решению задачи об ударе с отрывом.

Рассмотрим функционал

J w=2/

D

-( V ^) ² dx + ^ρ

ϕV n

S r

ds.

Будем считать, что он задан первоначально на множестве функций, дважды непрерывно дифференцируемых в области D, удовлетворяющих краевому условию на свободной гра- нице: ^|

S f

= 0, и имеющих первые производные непрерывные вплоть до границы области

D всюду, кроме, быть может, кривой, отделяющей твердое тело от свободной границы. На самом деле, как известно, на этой кривой первые производные могут обращаться в бес- конечность, и необходимо ввести некоторое ограничение на возможную сингулярность. Поэтому будем всегда предполагать, что у Е W^1) (D). Это означает, что кинетическая энергия, переданная жидкости при ударе, должна быть конечна. В дальнейшем решение краевой задачи, обладающее перечисленными свойствами регулярности, будем называть классическим.

Пусть граница ∂D — кусочно-гладкая, а функция ρ непрерывно дифференцируема в D и ограничена снизу положительным числом: —(x) > -о > 0. Предположим, что существует классическое решение краевой задачи о безотрывном ударе:

div ^-V^ = 0,                             (27)

ϕ

∂ϕ ∂n

= 0,

= 0,

S b

1 д^

—(x) дп

= V n .

S r

Предложение 2. Функция ϕ является точкой экстремума, даже строгого минимума, функционала J . Обратно, если функция ϕ обладает надлежащими свойствами регулярности и придает функционалу J минимальное значение, то она является классическим решением краевой задачи (27) - (30) .

Стандартное доказательство этого предложения опускаем. Хотя недостатки подобных «наивных» аналогов вариационного принципа Дирихле, сформулированных «на физическом уровне строгости», общеизвестны, предложение 2 указывает нам, как правильно определить обобщенное решение .

Обобщенное решение. Существование, единственность. Пусть D — ограниченная область с границей ∂D настолько регулярной, чтобы были применимы теоремы вложения С. Л. Соболева; кусочной гладкости для этого достаточно.

Определим гильбертово пространство H как замыкание множества C ^∞ -гладких функций, определенных в области D и исчезающих на свободной границе S f , по норме, порождаемой скалярным произведением

(У1, У2) = j ¹ V yi • V y2 dx.

D

Пространство H вложено в W^^D), когда D — ограниченная область или цилиндр, поскольку для таких областей справедливо неравенство Фридрихса.

Функционал J (у), определенный равенством (26), можно считать заданным на пространстве H . Действительно, по теореме вложения, для функции у G W ^¹ определен след на поверхности S r , причем сужение y | _s G L ^ (S r ) (общая формула в случае пространства w Pl )(D), D С R n , и s-мерного подмногообразия: q = n—p , что при n = 3, p = 2, l = 1, s = 2 и дает q = 4). Поэтому поверхностный интеграл в (26) определяет линейный ограниченный функционал на пространстве H , если V n G Ь 4 / з (В _т ). В наших условиях V n — даже ограниченная функция на S r .

Определение 1. Обобщенным решением краевой задачи (27)–(30) назовем функцию у G H и дающую минимум функционалу J (у).

Эквивалентное определение: назовем обобщенным решением задачи (27)–(30) функцию ϕ ∈ H , удовлетворяющую при любой функции η ∈ H интегральному тождеству

⁽У,П) н

ηV n dS.

S r

Существование и единственность такой функции ϕ непосредственно следуют из теоремы Рисса об общем виде линейного ограниченного функционала на гильбертовом пространстве.

Докажем эквивалентность двух определений — установим, что найденная функция у дает минимум функционалу J ( у ). Действительно, очевидная выкладка, с использованием равенства (32), показывает, что для любой η ∈ H справедливо равенство

J ⁽у + n) -JЫ^^П ) > 0,                  ⁽³³⁾

причем равенство возможно лишь при n = 0. Итак, доказана следующая теорема.

Теорема 1. Пусть D — ограниченная область с кусочно-гладкой границей ∂D . Тогда существует, и притом единственное, обобщенное решение задачи (27) - (30) .

Замечу, что фактически не была использована специальная форма функции V _n , и ее можно заменить любой функцией g G L4 / 3 (S r ).

Для классической задачи об ударе без отрыва, разумеется, хорошо известны результаты о регулярности решения. В частности, вполне стандартно доказывается, что внутри области D функция ϕ удовлетворяет уравнению (27) в классическом смысле, а если функция ρ достаточно гладкая, то можно обеспечить существование любого числа производных функции ϕ ; если ρ ∈ C ^∞ , то и ϕ есть C ^∞ -гладкая функция внутри области D . При надлежащей гладкости границы обобщенное решение ϕ удовлетворяет в классическом смысле и краевым условиям — всюду, кроме линий раздела твердого тела и свободной границы, а также дна и свободной границы. Особенности решения, возникающие на этих линиях, также хорошо изучены; весьма общая теория изложена в книге [10]. Во всяком случае известны асимптотики решения вблизи двугранных углов и конических точек.

• § 4.    Удар с отрывом

Сначала определим классическое решение этой задачи. Разумеется, оно должно удовлетворять уравнению (27) в обычном смысле, т. е., во всяком случае, иметь вторые непрерывные производные. Уравнение (27) эллиптично, так что гладкость решения ϕ внутри области D зависит лишь от гладкости функции ρ. Если ρ ∈ C ^∞ (напомню та к же, что мы предполагаем выполненным неравенство: p(x) > ро > 0 для всех x G D, с известной положительной константой ρ0), то и ϕ есть C ^∞ -гладкая функция внутри области D.

Теперь разберемся с краевыми условиями. На свободной границе S f условие у = 0 должно выполнят ь ся в классическом смысле: функция ϕ в точках поверхности S f , и даже на ее замыкании S f , непрерывна и принимает значение у = 0. Далее, граница твердого тела S r , как было уже сказано, делится на части S _r ⁼ и S _r ⁰ , причем на S _r ⁼ выполнено строгое неравенство ^(x) > 0 и краевое условие второго рода (9). На дополнительной части S0 (в зоне отрыва) выполнено равенство ^(x) = 0, а также строгое неравенство (8) для нормальной компоненты скорости. Предположим еще, что граничные кривые между S _r и S f , между S _r ⁰ и S _r ⁼ , а также между S _b и S f состоят из конечного числа кусочно-гладких кривых.

Нужно еще поставить дополнительное условие регулярности вблизи пересечений свободной границы с твердыми поверхностями S _r и S b — следует считать правилом, что в точках этих поверхностей граница области D теряет гладкость. Даже если поверхности S _r и S b гладкие, вообще говоря, имеет место особенность типа двугранного угла (обычного угла в двумерном случае). Разумеется, не исключено, что имеются ребра и конические точки на самих поверхностях твердого тела и дна — например, твердое тело может иметь форму параллелепипеда или конуса. Достаточным и физически оправданным ограничением является требование конечности энергии:

/ Р— dx = - / — ( V ^) ² dx <  го . (34)

J 2 2 J Р

DD

Это условие означает, что ϕ ∈ H , см. (31).

Теперь перейдем к изложению вариационного принципа для задачи об ударе с отрывом. Снова начнем с «наивного, на физическом уровне строгости», рассмотрения. Вернемся к прежнему функционалу

J =

2 у^-^)2 dx +у ^V n ds D               S r

на пространстве H . В пространстве H определим (выпуклый, замкнутый) конус K , состоящий из функций ϕ , принимающих почти всюду в D неотрицательные значения: ^(x) > 0 почти для всех x G D.

Предложение 3. Предположим, что ϕ 0 — классическое решение задачи об ударе с отрывом. Тогда функционал J достигает своего строгого минимума на конусе K в точке ϕ 0 . В частности, это означает, что такая точка минимума единственна.

• <1 Пусть ^ — произвольная функция из конуса K . Положим ^ = у о + п и рассмотрим разность J (^о + п) — J (^о). После интегрирования по частям получаем

  J ⁽^о ^{+ п)} -J ⁽^о)= / ⁿ~~^~^{dS +} ρ ∂n

  ∂D

  
  
  
  

  j ( V n)2

  D

  
  

  dx + j nV n

  
  

  dS.

  
  
  
  

  S r

  
  

Другой объемный интеграл пропал, поскольку уо — решение уравнения (27). С учетом краевых условий на S = и S b , получаем

J (у) -J (уо)= /n f¹    + V.) dS + ¹ /^( V n) ² dx.

J    \ - dn /       2 J -

^S r ^{0                             D}

Подчеркну, что интеграл по поверхности S b исчез потому, что отрыв на жен, согласно предложению 1.

Поверхностный интеграл в (37) неотрицателен. В самом деле, у(x) = 0 как всюду уо + n > 0, из этого неравенства следует, что n(x) > 0 на S ( °.

ней невозмо-

на S ( ? , а так Второй мно-

житель в этом интеграле неотрицателен, ввиду условий (8)–(9). Из неотрицательности поверхностного интеграла в (37) следует неравенство

J (у) -J (уо) > ¹ /'¹(^Vn) ² dx. 2 J -

D

Кроме того, очевидно, что при у = уо интеграл справа в (38) положителен. Поэтому у о — точка строгого минимума функционала J на конусе K . B

Предложение 4. Предположим, что функционал J достигает своего минимума на

K в точке у о Е K:

inf J (х) = J (уо). χ ∈ K

Допустим, что функция уо достаточно регулярна. Тогда она является решением краевой задачи для уравнения (27) с обычными краевыми условиями (28) и (29) на свободной границе и на неподвижном дне, а также и условиями на подвижной твердой границе S r (см. (8) - (9)) :

у ₀ (x) > 0, x Е

1 ■'+V. > о, ρ ∂n дуо   п

—— = 0, x ∂n

При этом всякий раз, когда у(x) > 0 в точке

S b ∪ S r ,

x ∈ S r ,

∈ S b .

x ∈ S _r , в этой точке соответствующее

неравенство в (41) превращается в равенство. Итак, у о — классическое решение.

<1 Пусть n Е H и обладает тем свойством, что у о + en Е K при всех достаточно малых положительных ε, такую функцию η назовем допустимой. Тогда из условия минимума (39) следует неравенство

d+ dε

J (уо + en) >  0, е =о

d+                      Ч где dε — правая производная. Это неравенство переписывается в виде у - Vуо • Vn dx + У nV. dS > 0

D

Sr и должно выполняться для всех допустимых η . После интегрирования по частям, которое законно, ввиду предполагаемой гладкости функции уо, получаем неравенство

- j n div 0 V уо^ dx + У

D

S b

1 дуо       Л дуо,тЛ дс^п n dS + n —й + V. dS > 0.

ρ ∂n          ρ ∂n

S r

Из (45) сразу следует, что функция ϕ0 в области D удовлетворяет дифференциальному неравенству

div ^- V ^ o^ 6 0.

Действительно, если бы в какой-нибудь точке x0 ∈ D выполнялось противоположное неравенство, то, по непрерывности, оно сохранялось бы и в некоторой окрестности этой точки. Но тогда, выбирая неотрицательную функцию η с носителем в этой окрестности и совпадающую с левой частью (46) в несколько более узкой окрестности, придем к противоречию с неравенством (45) (конечно, окрестность выбирается столь малой, что она целиком лежит в области D, так что поверхностные интегралы исчезают).

Из (46), как известно, следует, что ϕ0 не может достигать минимума внутри области D. Поэтому ^o(x) > 0 для всех x G D, поскольку минимум достигается на S f и равен нулю. Мы применяем здесь сильный принцип максимума для эллиптического оператора (см., например, [6, 7]).

Но если ^o(x) > 0 в некоторой точке x G D, а значит и в ее достаточно малой окрестности, то в этой окрестности на допустимую функцию η уже нет ограничений знака. Поэтому можно выбрать ее в этой окрестности финитной и неположительной, даже совпадающей с div (рV^o) в несколько меньшей окрестности. Получаемое таким путем противоречие с (45) показывает, что всюду в области D выполняется не просто неравенство (46), а уравнение (27): Ар^ = 0. Теперь в неравенстве (45) объемный интеграл исчезает, и оно принимает вид jп^ dS + /п (-^ ' Vn) dS > 0             4 7

Sb                   Sr для всех допустимых функций η ∈ H .

Сначала докажем, что выполняется краевое условие (42) на неподвижном дне S b . Пусть xo G S b . Рассмотрим два варианта: 1) ^o(xo) = 0, 2) ^o(xo) > 0. В первом случае

∂ϕ0

очевидно, что

∂n

6 0. (Более того, согласно лемме о граничной точке ([6, с. 41], x0

∂ϕ0

принадлежащей Э. Хопфу и О. Олейнику, имеем неравенство ∂n

< 0). Иначе в об- x0

ласти D вблизи точки x0 нашлись бы точки, в которых ϕ0 принимает отрицательные значения (напомним, что n — орт внешней нормали). Но это приводит к противоречию с неравенством (47). Действительно, выбирая функцию η финитной, ненулевой и неотрицательной, с носителем в малой окрестности точки x0, увидим, что второй интеграл (47) исчезает, а первый — отрицателен. Итак, случай 1) невозможен. Мы повторили здесь, по существу, доказательство предложения 1.

В случае 2), когда ^o(xo) > 0, в окрестности точки xo отпадает ограничение знака на функцию η . Выбирая ее так, чтобы в малой окрестности точки x0 она имела знак противоположный ^∂ _∂ ^ϕ _n ⁰ , а вне несколько большей окрестности исчезала, мы придем к противоречию с предположением, что дА ⁰ = 0. Таким образом, функция ^o на неподвижном дне S b удовлетворяет краевому условию (42).

Теперь неравенство (47) принимает вид

/ ^п (-^Г ⁺ V n) ^dS >  ° -

S r

Пусть x0 ∈ S _r . Поскольку всякая неотрицательная функция η ∈ H допустима, из неравенства (48) сразу следует, что выражение в круглых скобках неотрицательно. Таким образом, неравенство (41) выполнено всюду на S _r .

Далее, если ^(xg) > 0, то в окрестности точки xo функцию п можно выбрать знакопостоянной, и притом противоположного знака с выражением в круглых скобках. (Снова пользуемся тем, что ограничение знака отпало.) Тогда из (47) выводим, что в такой точке выполнено краевое условие

¹    + V n = 0.                                (49)

ρ ∂n

Это заканчивает доказательство предложения 4. B

Заметим, что в каждой точке x Е S r , где неравенство (41) строгое, yо(x) = 0. Вместе с тем, в некоторых точках поверхности S r могут одновременно выполняться равенства уо = 0 и p—dn o + V n = 0. Это, например, происходит в точках раздела зоны отрыва S0 и безотрывной зоны S _r ⁼ . Нетрудно также увидеть, что в каждой точке границы S r , в которой неравенство (41) — строгое, выполнено краевое условие у = 0.

Предложения 3 и 4 оправдывают следующее определение обобщенного решения задачи об ударе с отрывом.

Определение 2. Обобщенным решением краевой задачи (8)–(12) назовем функцию ϕ ∈ H, которая реализует минимум функционала J на конусе K.

Теорема 2. Обобщенное решение краевой задачи об ударе с отрывом существует и единственно.

C Пусть ϕ _∗ — решение задачи о безотрывном ударе, точнее, обобщенное решение краевой задачи (27)–(30) с отброшенным условием положительности потенциала. Полагая у = у * + п, преобразуем J (у * + п):

J (у * + п ) — J (у * ) + ^Еу , • V n dx + j пV n dS + |у^п)2 dx.       (50)

D

S r             D

Заметим, что сумма второго и третьего слагаемых равна нулю, поскольку ϕ _∗ — критическая точка функционала J на пространстве H . Поэтому справедливо равенство

J ^(y) = ^ k ^{y — у}*112⁺ J ^(y * ), ⁽⁵i) где J (у * ) — несущественная константа. Согласно лемме о проекторе, минимум функционала J на конусе K существует и единственен, а потому это строгий минимум. Таким образом, обобщенное решение задачи об ударе с отрывом есть проекция безотрывного решения ϕ _∗ на конус неотрицательных функций K в H :

уо — Pk у * . B

В вариационном исчислении имеется эвристический принцип, согласно которому на то множество, по которому берется минимум функционала, можно накладывать любые ограничения, которые заведомо выполнены для минимизирующей функции. В нашем случае нетрудно установить, что обобщенное решение ϕ 0 удовлетворяет эллиптическому уравнению (27) всюду в области D . Поэтому справедлив и такой вариационный принцип: обобщенное решение ϕ 0 задачи об ударе с отрывом дает строгий минимум функционалу

J 1 (y) = о / -(V y — V y * ) ² dx

2 J р

D на множестве ρ-гармонических функций, принадлежащих гильбертову пространству H .