Ограниченность потенциала Рисса в весовых обобщенных гранд-пространствах Лебега
Автор: Умархаджиев Салаудин Мусаевич
Журнал: Владикавказский математический журнал @vmj-ru
Статья в выпуске: 2 т.16, 2014 года.
Бесплатный доступ
Доказана теорема о двухвесовой ограниченности линейных операторов во введенных нами ранее обобщенных гранд-пространствах Лебега. С помощью этой теоремы получены двухвесовые оценки нормы потенциала Рисса в рассматриваемых пространствах.
Обобщенное гранд-пространство лебега, потенциал рисса, интерполяционная теорема, весовые оценки
Короткий адрес: https://sciup.org/14318463
IDR: 14318463 | УДК: 517.968
Текст научной статьи Ограниченность потенциала Рисса в весовых обобщенных гранд-пространствах Лебега
Неравенство Соболева. [2]
kIa fkLq
(Rn) 6
ckf
11
lp
(Rn), 1
to,
1/q = 1/p
-
a/n,
(1)
для потенциала. Рисса.
I
af
:=
1 Iх
—
yla-nf (y) dy,
0<
a
< n
Rn в пространствах Лебега Lp(Rn) имеет известные весовые обобщения, полученные в работах В. Кокилашвили [1, 15, 16], Е. Т. Sawyer [25], Е. Т. Sawyer и R. L. Weeden [26], С. Рй« [23, 24]. S. Tord |30].
В этой работе мы рассматриваем потенциалы Рисса. в весовых обобщенных
гранд-пространствах Лебега L^(Rn,w).
В 1992 г. Т. Iwaniec и С. Sbordone [13] ввели
grand Lebesgue spaces (гранд-пространства Лебега^
по ограниченному множеству Н С Rn следующим определением:
θ
Up'6
(Щ =
f
: sup
е
p-E
||f kLp-E(Q) <
to
, 1
to,
6 >
0.
0 Операторы гармонического анализа, интенсивно исследовались в таких пространствах в последние годы; они продолжают привлекать внимание исследователей в связи с различными приложениями [5, 6], [8-12], [14], [17-21]. В [27, 28] был предложен подход, позволяющий ввести гранд-пространства Лебега, на. множествах неограниченной меры. В наиболее общей форме этот подход реализован в [3] в виде A'6 (H,w) θ = f : sup е p- kf kLP-E(Q'WttE) < TO , 0 где 1 < p < то. 6 > 0 ii Q С Rn — произвольное открытос множество: в случае 6 = 1 пишут Lp(Q,w) := Lp,1(Q,w) , и Up'6(Rn,w) = Up'6(Rn,w) | — в случае a = 1. I a=1 Весовое обобщенное гранд-пространство Лебега Lp)'6(Q, w) зависит от «функционального параметра » a ii является расширенном классического пространства Лебега Lp(Q,w) при условии a Е Lp(Q,w). В работах [3, 27] с помощью теремы Рисса. - Торина. - Стейна. - Вейса, об интерполировании с изменением меры показано, что ограниченность произвольного линейного оператора, в двух «близких друг к другу» обычных весовых пространствах Лебега, влечет ограниченность в весовом гранд-пространстве Лебега. На основе этого в [3] доказана. ограниченность операторов Кальдерона. — Зигмунда, и максимального оператора. Харди - Литтлвуда, в весовых гранд-пространствах Лебега. Основная цель данной работы — исследование действия потенциала. Рисса. во введенных в [3] весовых обобщенных гранд-пространствах Лебега. Для этого мы сначала, в теореме 3.1, применением той же теремы Рисса. - Торина. - Стейна. - Вейса, получаем двухвесовые оценки для линейных операторов в рассматриваемых весовых гранд-пространствах. Как следствие из этих оценок и свойств весов Макенхаупта. — Уидена, получаем основное утверждение — теорему 4.2 об ограниченности потенциала. Рисса. в весовых обобщенных гранд-пространствах Лебега. Обозначения. C, c — различные абсолютные положительные постоянные, которые могут иметь различные значения даже в одной и той же строке; Q — открытое множество в Rn: |A| - мора Лебега измерпмого множества A С Rn: v. w - веа на. Q. т. е. неотрицательные локально интегрируемые на Q функции, обращающиеся в нуль на множестве нулевой меры: w(E) = JE w(x) dx; B(x,r) = {y Е Rn : |y — x| < r}; B(x,r) = B(x,r) П Q: Q - куб в Rn e ребрами, параллельными координатным осям: ^ означает непрерывное p вложение: p = — p—1 2. Предварительные сведения 2.1. Определения и вспомогательные утверждения. Через Ap, 1 < p < ∞, обозначаем класс весовых функций, удовлетворяющих условию Макенхаупта. [22]: p—1 Q⊂Rn |Q| 1 - i w(x) dx I I w(x) p-1dx I < то. |Q| QQ ОПРЕДЕЛЕНИЕ 2.1. Будем говорить, что пара весов (w,v) принадлежит классу Ap,q, 0 < a < n. 1 < p, q < то [26]. если sup |Q|a/n+1/q 1/p f 777 / v(x) dx! f / w(x)1 p0 dx! < то. Q⊂Rn |Q| |Q| QQ ОПРЕДЕЛЕНИЕ 2.2. Будем говорить, что пара весов (w,v) принадлежит классу A*(p, q). 1 < p, q < то [7]. если ™Р Q⊂Rn |Q| 1/q 1 0 1/p0 v(x)qdx w(x) pdx< то |Q| QQ Лемма 2.3. Пусть 0 < a < п, 1 < p, q < той выполнены условия 1) для БОСОВЫх функций w п v существуют числа r > 1 и 0 < Е < q — 1 такие. что sup |Q|a/n+1/(q-e)-1/p Q j v(x)rdx Q 1 (q-e^r j w(x)(1-p)r dx Q 1 p0 r < то; 2) исотрипательпыс функции a ii b таковы, что существует число 5 > е такое, что δδ (ap, bq-E) G A*(p, q — е). Павла (wae,vbe) G Aa«_.. p,q-ε C Обозначим △ := sup |Q|a/n+1/(q-e)-1/p _ v(x)b(x)e dx QcRn |Q| Q 1/(q-e) 1 \ 1/P0 [w(x)a(x)e]1 p dx I |Q| Q . К обоим интегралам применим неравенство Гёльдера с показателем r > 1. Получим △ 6 sup Q⊂Rn |Q|a/n+l/(q-e)-l/p ТОТ Уv(x) dx) Q 1 r(q-e) г1! /w(x)(1 p0)r dx] |Q| Q 1 rp0 jQ / [b(x)C<,,q-C)] "Ч ”' (тот / [a QQ Откуда следует утверждение леммы. B В случае 0 < a < п. 1 < p < n/a. 1/q = 1/p — a/n известно соотношение (wp/q, w) G Ap,q<> w G A1+q/p0. 2. 2. Ограниченность риссова потенциала в весовых пространствах Лебега. Будем говорить, что вес w удовлетворяет условию удвоения. если существует C > 0 такое. Tito w(2Q) 6 Cw(Q) для все.т кчбов Q С Rn е ребрами, пара.тлелвпымп координатным осям. Основное утверждение данной статьи получено посредством теоремы Сойера. - Уидена [26] об ограниченности оператора потенциала Ia в классических пространствах Лебега: Теорема 2.4. Пусть 0 < a < п, 1 < p 6 q < то. (1) Неравенство IIIaf Ны(Rn,v) 6ckfkLP(Rn,w) выполняется, если существует r > 1 такое, что sup |Q|a/n+1/q-1/py f v(x)rdx Q Q 1/(p0r) < то. Q (2) Если предподожить, что p < q и функции v и w1 p удовлетворяют условию удвоения, то (4) выполняется тогда и только тогда, когда (w,v) G A“q. 2. 3. Интерполяционная теорема. Нам понадобится следующая интерполяционная теорема. Рисса. - Торина. - Стейна. - Вейса, с изменением меры [4, 29], которую мы формулируем в весовых терминах. Теорема 2.5. Пусть pk, qk G [1, то) ii vk, wk - всca па. Q. k — 1, 2, и T - сублинейный оператор, опрелелеппый па Lp (Q,wi) П Lp2(Q,w2). Если T : Lp(Q,wi) ^ Lq1 (Q,v1) с нормой Mi 11 T : Lp2 (Q, w2) ^ Lq2 (Q, v2) с no]>мой M2. to T : Lp (Q,wt) ^ Lqt (Q,vt) с нормой M 6 Mi tM2- где -— (— Pt Pi P2 Pi = qt qi q2 qi (i-t) pt tpt pp wt - wi 1 w2 2 , (i-t) qt t qt vt — vi q1 v2q2, 0 < t < 1. 3. Ограниченность линейных операторов в обобщенных гранд-пространствах Лебега Теорема 3.1. Пусть 1 < p, q < то, w и v — два веса на Q С Rn. Пусть линейный оператор T ограничен из пространства Lp(Q,w) в просдыпетво Lq(Q,v) н ограничен из пространства Lp0 (Q,wap-p0) ii просдпапство Lq0 (Q,vbq-q0) для некоторая двух чисел 1 < Po Тогда оператор T ограничен из весового обобщенного гранд-пространств а Лебега La)6(Q,w) в весовое обобщенное гранд-пространство Лебега Lq),6q/p(Q,v). C Для произвольного положитолыюго числа 9i имеем θ1 kTf k q)i)A(O —= sup £q-E kTf kLq-^(Q,vb^) — max{A, B}, Lb UCv) 0 A — sup £q-e kTf kLq-E(n,vbE), B — sup £q-- ||Tf kLq-E(n,vbE). (8) O Оценка величины A. По интерполяционной теореме 2.5 с параметрами Pi — P, P2 — P0 , qi — q, q2 — q0 , vi — w, v2 — wap-p0 , wi — v, w2 — vbq-q0 получаем, что kTf kLq-(Q,vbE) 6 Mi tMtkf kLPE(U,waP-PE), Pe — (p + t (p0 - p)) , t — (q-q^q-e) ДЛЯ ECCX£ G [0, q - qo]. Следовательно. A 6 sup Mi1 tM2t£q-E kf |lp.(Q,waP-pE) O 6 sup O θ1 -θ θ Mi M.t£ q-- (p - Pe) P- sup (p - Pe) P- kf |lp- (Q,woP-PE) - O Учитывая, что t = pp^p-pj, получим A 6 C(po,qo)kf kLp),e(Q,w), где -8( 1-t+-t 9i (1-t+-t- C(Po,qo)= sup M^ tMt 0 tq(q — qo) q q° tp(p — po) p p° qo + t(q — qo) po + t(p — po) Выделив из правой части сомножитель t81 q-8p. можно сделать вывод: константа C (Po,qo) коцепи а. если 91 = p 9. Оценка величины B. Воспользовавшись неравенством Вёльдера с показателем ^°- > 1. полечим q-ε q( ^ - ^ kTf ih-^ 6 iwiLq-v) q° kTf kLq° (Q,vbq-q°), так что 61 q( --- - - B 6 SuP E q- kbkLq q" q°j kTf |^° (Q,vbq-q° ) q-q° - 61 - 61 KL_ 61 = (q—qo) q° kbkLqq(°Q v) sup Eq- IlbllL-(q v)(q—qo) q° kTf1Ь°(Q,vbq-q°) ’ q-q° 6 inf fh-1(q — qo) sup h(e)) • A = A- o -61 - где обозначено h(e) := eq-E ||bkLq(q v). Объединяя оценки для A и B, получим утверждение теоремы 3.1. B {M1( Р ) 6 ,M2( Р ) p° }• Замечание 3.2. В случае p° = p справедтнво C(po,qo) = max 4. Основное утверждение В работе [21] получено необходимое и достаточное условие ограниченности потенциала Висса в весовом гранд-пространстве Лебега на отрезке [0,1]: Теорема 4.1. Пусть 0 < а < 1.1 < p < ж 9 > 0 iiq = p/(1 — ар). Тогда неравенство IIIa(fwa)kLq),6<1+aq)([o,1],w) 6 ckfIIlpI6([o,1],w) выполняется тогда и только тогда, когда w € A1+q/po • Ha основании теоремы 3.1 мы можем получить двухвесовую оценку нормы потенциала Висса по Rn в весовых обобщенных гранд-пространствах Лебега: Теорема 4.2. Пусть 0 < а< n 11 1 го. Пусть 1) (w,v) е Aaq: 2) v и w1 pудовлетворяют условию удвоения; 3) для тжотс>рых ппсел r> 1 н 0 < Eo sup |Q|a/n+1/(q-=°)-1/p°f [ v(x)rdx Q Q ' °r . < ∞, po 6 q — Eo; Q 4) неотрннателвiibic (1>ункпнн a ii b таковвк что существует число 5 > Eo такое, что о ap° , bq-E° I € A*(po, q — Eo) и функции vbe° и (wa 13)1 p° удовлетворяют условию удвое ния. Тогда оператор Рисса Ia ограничен из обобщенного гранд-пространства Лебега Lp’^(Rn,w) в обобщенное гранд-пространство Лебега Lq,6q/p(Rn, v), 0 > 0. C Из условий 1) и 2) в силу теоремы 2.4 следует ограниченность оператора Рисса из пространства Lp(Q, w) в пространство Lq(Q, v), из условий 3) и 4) на основании леммы 2.3 и теоремы 2.4 следует его ограниченность из пространства LPo(Q,wae0) в пространство Lq-e0(Q,vbe0). Таким образом, условия теоремы 3.1 выполнены и тем самым теорема 4.2 доказана, в Следствие 4.3. Пусть Q С Rn 0 < a < n, 1 n/a, 1/q = 1/p — a/n, w E A1+q/p? II функции w II w-p/q удовлетворяют условию удвоения. Тогда Ia : Lp’6fowp/q) ^ Lq’6q/p(Q,w). C Из соотношения (3) еле дует, что пара функций (wp/q ,w удовлетворяет условию 1) теоремы 4.2. Следовательно, w E A1+ q. Существует число e > 0 такое, что w E A1+q_е. p0p Решив систему уравнений q-r0 = pq?—e, q—— = p-- а ПОЛУЧИм числа pg и eq, для которых имеет место соотношение A1+q = A q-E0 . Откуда следует выполнимость условия 3) 01+ ppo теоремы 4.2. Первая часть условия 4) выполняется, так как класс Ap,q содержит константу, а вторая — совпадает с условием 2). Таким образом, все условия теоремы 4.2 выполнены и следствие доказано. B Отметим, что в случае отрезка [0,1] теорема 4.2 содержит достаточную частью теоремы 4.1 при выборе w = w1-ap, v = w, b = 1, a = wa. Автор выражает искреннюю благодарность профессору С. Г. Самко за. полезные замечания, способствовшие улучшению содержания статьи.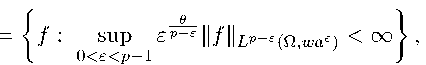
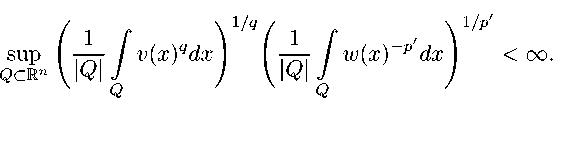
двух i юотрппателышх па Q фкшишй a G Lp(Q,w) н bG Lq (Q.v).
— 1 выполняется условие
Список литературы Ограниченность потенциала Рисса в весовых обобщенных гранд-пространствах Лебега
- Кокилашвили В. Максимальные функции и интегралы типа потенциала в весовых пространствах Лебега и Лоренца//Тр. Мат. ин-та АН СССР.-1985.-Vol. 172.-C. 192-201.
- Соболев С. Л. Об одной теореме функционального анализа//Мат. сб.-1938.-Vol. 4(3).-C. 471-497.
- Умархаджиев С. М. Обобщение понятия гранд-пространства Лебега//Изв. вузов. Математика.-2014.-Vol. 4.-C. 42-51.
- Bergh J., Lofstrom J. Interpolation Spaces. An Introduction.-Berlin: Springer, 1976.-207 p.
- Capone C., Fiorenza A. On small Lebesgue spaces//J. Function Spaces and Appl.-2005.-Vol. 3.-P. 73-89.
- Di Fratta G., Fiorenza A. A direct approach to the duality of grand and small Lebesgue spaces//Nonlinear Analysis: Theory, Methods and Applications.-2009.-Vol. 70, № 7.-P. 2582-2592.
- Ding Y., Lin C.-C. Two-weight norm inequalities for the rough fractional integrals//Int. J. Math. Math. Sci.-2001.-Vol. 25, № 8.-P. 517-524.
- Fiorenza A., Gupta B., Jain P. The maximal theorem in weighted grand Lebesgue spaces//Studia Math.-2008.-Vol. 188, № 2.-P. 123-133.
- Fiorenza A. Duality and reflexivity in grand Lebesgue spaces//Collect. Math.-2000.-Vol. 51, № 2.-P. 131-148.
- Fiorenza A., Karadzhov G. E. Grand and small Lebesgue spaces and their analogs//J. Anal. Appl.-2004.-Vol. 23, № 4.-P. 657-681.
- Fiorenza A., Rakotoson J. M. Petits espaces de Lebesgue et leurs applications//C.R.A.S. t.-2001.-Vol. 333.-P. 1-4.
- Greco L., Iwaniec T., Sbordone C. Inverting the $p$-harmonic operator//Manuscripta Math.-1997.-Vol. 92.-P. 249-258.
- Iwaniec T., Sbordone C. On the integrability of the Jacobian under minimal hypotheses//Arch. Rational Mech. Anal.-1992.-Vol. 119.-P. 129-143.
- Kokilashvili V., Meskhi A. A note on the boundedness of the Hilbert transform in weighted grand Lebesgue spaces//Georgian Math. J.-2009.-Vol. 16, № 3.-P. 547-551.
- Kokilashvili V. Two-weighted estimates for some integral transforms in Lebesgue spaces with mixed norm and imbedding theorems//Georgian Math. J.-1994.-Vol. 1, № 5.-P. 495-503.
- Kokilashvili V. On a progress in the theory of integral operators in weighted Banach function spaces//Function Spaces, Differential Operators and Nonlinear Analysis. Proc. of the Conf. held in Milovy, Bohemian-Moravian Uplands, May 28 -June 2, 2004.-Praha: Math. Inst. Acad. Sci. Czech Republick, 2005.-P. 152-175.
- Kokilashvili V. Boundedness criterion for the Cauchy singular integral operator in weighted grand Lebesgue spaces and application to the Riemann problem//Proc. A. Razmadze Math. Inst.-2009.-Vol. 151.-P. 129-133.
- Kokilashvili V. The Riemann boundary value problem for analytic functions in the frame of grand ${L^{p)$ spaces//Bull. Georgian Nat. Acad. Sci.-2010.-Vol. 4, № 1.-P. 5-7.
- Kokilashvili V., Samko S. Boundedness of weighted singular integral operators on a Carleson curves in Grand Lebesgue spaces//ICNAAM 2010: Intern. Conf. Numer. Anal. Appl. Math.-Vol. 1281.-P. 490-493.
- Kokilashvili V., Samko S. Boundedness of weighted singular integral operators in Grand Lebesgue spaces//Georg. Math. J.-2011.-Vol. 18, № 2.-P. 259-269.
- Meskhi A. Criteria for the boundedness of potential operators in grand Lebesgue spaces.-arXiv:1007.1185.
- Muckenhoupt B. Weighted norm inequalities for the Hardy maximal function//Trans. Amer. Math. Soc.-1972.-Vol. 165.-P. 207-226.
- Perez C. Two weighted norm inequalities for Riesz potetials and uniform ${L^p$-weighted {Sobolev inequalities//Indiana Univ. Math. J.-1990.-Vol. 39, № 1.-P. 31-44.
- Perez C. Two weighted inequalities for potetial and fractional type maximal operators//Indiana Univ. Math. J.-1994.-Vol. 43, № 2.-P. 663-683.
- Sawyer E. T. A two weight weak type inequality for fractional integrals//Trans. Amer. Math. Soc.-1984.-Vol. 281, № 1.-P. 339-345.
- Sawyer E. T., Weeden R. L. Weighted inequalities for fractional integrals on euclidean and homogeneous spaces//Amer. J. Math.-1992.-Vol. 114, № 4.-P. 813-874.
- Samko S. G., Umarkhadzhiev S. M. On Iwaniec-Sbordone spaces on sets which may have infinite measure//Azerb. J. Math.-2011.-Vol. 1, № 1.-P. 67-84.
- Samko S. G., Umarkhadzhiev S. M. On Iwaniec-Sbordone spaces on sets which may have infinite measure: addendum//Azerb. J. Math.-2011.-Vol. 1, № 2.-P. 143-144.
- Stein E. M., Weiss G. Interpolation of operators with change of measures//Trans. Amer. Math. Soc.-1958.-Vol. 87.-P. 159-172.
- Tord S. Weighted norm inequalities for {Riesz potentials and fractional maximal functions in mixed norm {Lebesgue spaces//Stud. Math.-1990.-Vol. 97, № 3.-P. 239-244.


