On a limit pass from two-point to one-point interaction in a one dimensional quantum mechanical problem giving rise to a spontaneous symmetry breaking

This work is a direct continuation of the papers [1] and [2]. In particular, [2] contains our detailed motivation to the present studies and a sketch concerning the history of corresponding problems (see also [3] and [4], for the present state of this approach see [5] and [6] ). Because of this, we not mention here the related historical aspects. We consider the spontaneous symmetry breaking (see [7] and [8]) in one dimensional quantum mechanical problems in terms of two-point boundary problems with entanglement which leads to singular potentials (the derivative of two tied shifted delta-functions).

In Section 1 we recall some well known results concerning a Hamiltonian with one-point interaction. In Section 2 we present some results on the study of singular potentials in terms of shifted delta-functions or their first derivative. In particular, we discuss a Hamiltonian (containing a two-point interaction) whose ground state is degenerate, with two eigenfunctions. Next, in Section 3 we go to the main contribution of the paper using different forms of limit pass from two-point interaction to one-point one. In particular, a selfadjoint extension of a limit differential operator to a larger Pontryagin space preserves an option of degenerate ground state, moreover, the corresponding Hamiltonian contains the second derivative of delta-function. Finally, we give our conclusions in Section 4.

1.    Prologue

Our principal aim is a pass from two-point interaction to one-point one, so we need to recall some basic facts concerning one-point interaction. Let the differential operator D 0 = -d ² • /dx² have the domain

D (D o ) = { y(x) | y(x) G W ² ’ ² ( R ), y(0) = y ‘ (0) = 0 } ,                   (1)

where W ^{2 , 2} ( R ) is the corresponding Sobolev space. Its adjoint one Dq has the domain

D (D 0 ) = { y(x) | y(x) | R + G W ^{2 , 2} ( R + ), y(x) | R - G W ² ’ ² ( R — ) } ,               (2)

where R ₊ = { x | x > 0 } and R _- = { x | x < 0 } , so x(t) , x'(t) are absolutely continuous functions in the both open half-lines R _- and R ₊ , but, generally speaking, are not defined at zero. At the same time, the following left- and right-hand limits y( - 0) = 1 0m 0 y(x) , y ‘ ( — 0) = lim y ‘ (x) , y (+0) = lim y (x) and y ‘ (+0) = lim y ‘ (x) are well defined.

x ^ 0 ,x< 0                 x ^ 0 ,x> 0                     x ^ 0 ,x> 0

Evidently D0 ⊂ D0∗ , so D0 ⊂ D0 ⊂ D0∗ for every selfadjoint extension D0 of D0. Thus, any extension of D0 can be obtained as a restriction of D0∗ . A simple calculation yields (D0y, z) = -y‘(-0)z(-0) + y‘(+0)z(+0) + y(-0)z‘(-0) - y(+0)z'(+0) + (y, D0z). Therefore, any selfadjoint restriction of D0∗ must be such that y‘(+0)z(+0) - y‘(-0)z(-0) - y(+0)z‘(+0) + y(-0)z‘(-0) = 0.          (3)

Any set of boundary values (y( - 0), y ‘ ( - 0), y(+0), y ‘ (+0)) can be considered as an element of a four-dimensional pseudo-unitary space (for the terminology see [9]) and Equality (3) means that for any selfadjoint restriction the corresponding sets must form a twodimensional neutral subspace. Alternatively, for a selfadjoint restriction one need to define two suitable linear homogenous conditions. Some of these accept jumps at zero for y (x) and/or y ‘ (x) . The latter is well known (see the book [5]) and can be interpreted as the Hamiltonian with one-point interaction involving delta-function and/or its first derivative. In [5] also singular potentials with derivatives of the shifted delta-function in finitely many points were discussed, but this discussion was restricted to local boundary conditions only. For historical details see also [6]. Within the frame of one-point problem there are some selfadjoint extensions with two negative eigenvalues [10]: for D 0 given by the boundary conditions ( a > 0, в >  0 )

a(y ⁽⁺⁰⁾ + y ^{( - 0})) = ( ^- y ‘ ⁽⁺⁰⁾ + y ‘ ^{( - 0)}), ^e(y^{(+0) -} y ^{( - 0)}) = ^- (y ‘ ^{(+0) +} y ‘ ^{( - 0)}),

conditions (3) are fulfilled, so it is selfadjoint. This extension has the eigenvalues - α ² and - в ² with the eigenfunctions e ^{- a | x |} and Sgn(x)e ^{- e | x |} respectively ( Sgn (x) = - 1 for x < 0 , Sgn (0) = 0 , Sgn (x) = 1 for x > 0 ) and D ₀ y(x) = - y ‘‘ (x) - в • ^ ‘ (x) (y ‘ ( - 0) + y ‘ (+0)) - a • 5(x)(y( - 0)+ y (+0)) .

Let a = в . The latter means that D0 has the unique negative eigenvalue -a2 with two non symmetric eigenfunctions y1(t) =

e^ax ,  if x < 0,

0, if x > 0

and y 2 (x) =

0, if x < 0, e-^ax , if x > 0.

The case in question does not represent a model related with a spontaneous symmetry breaking. Indeed, the latter is the case of a non transitable barrier: Conditions (4) imply a • y ( - 0) = y ' ( — 0) and a • y(+0) = —y ‘ (+0) , so the waves with support on R _- and R ₊ are independent. Selfadjoint extensions of this type were named in [6] separated .

In next sections we will consider some analogous schemes for boundary problems at two interior points —h, h and a behavior of the corresponding extensions if h ^ 0 .

2.    Two-Point Interaction 2.1.    An Underlying Idea

Let the differential operator D _h = —d ² • /dx ² have the domain D(D _h ) = {y (x) | y (x) E W ^{2 , 2} ( R ), y(±h) = y ' (±h) = 0 } . Then the adjoint operator D h has the domain

D (D h ) = {y(x) | y(x) | R - h E W ^{2 , 2} ( R - h ),y (x)\ ₍- h,h ) E W ^{2 , 2} ((—h,h)), y (x) | R h E W ^{2 , 2} ( R h )}, where R _-h = (—to, — h) , R _h = (h, +to) . A restriction of D h is selfadjoint for any collection of four linearly independent homogenous boundary conditions that yields

—y'(—h — 0)z(—h — 0) + y ' ( — h + 0)z(—h + 0) — y 'hi — 0)z(h — 0) +

+y 'hi + 0)z(h + 0) + y (—h — 0)z'(—h — 0) — y (—h + 0)z'(—h + 0)+        (5)

+y (h — 0)z'(h — 0) — y(h + 0)z'(h + 0) = 0.

Using this way one can, for example, put

y(—h — 0) = y(—h + 0), y(h — 0) = y(h + 0) ,                  (6)

and the same for z ( x ) , that yields the continuity of y and z . The latter converts (5) to

(y'(—h + 0) — y'(—h — 0))z( — h) + (y'(h + 0) — y 'hi — 0))z(h) —

—y (—h)(z'(—h + 0) — z'(—h — 0)) — y(h)(z'(h + 0) — z'(h — 0)) = 0.

An important part of this case (including an entanglement of boundary conditions) was analyzed in [1]. In particular, it was shown that under some restrictions and h ^ 0 Conditions (6), (7) convert to Conditions (4).

Next, let D _reg be the selfadjoint differential operator given by the formal differential expression D reg = — d ² • /dt with the domain D(D reg ) = {y(t)\ y(t) E W ^{2 , 2} ( R ) } . Let

G(t)

e - γ | t |

2Y

Then for every z(t) E L ² ( R ) and y >  0

+ ^

(Y ² 1 + D reg ) 1 z(t)

У z ( t )G(t — т)dT .

-∞

Note that D _reg is the restriction of D _h ^∗ generated (see (5)) by the boundary conditions

y(—h — 0) = y(—h + 0),    y(h — 0) = y(h + 0), y'(—h — 0) = y'(—h + 0), y'(h — 0) = y'(h + 0).

• 2.2.    An Entanglement of Boundary Conditions: Continuous First Derivative

In this subsection we assume y'(—h — 0) = y'(—h + 0), y'(h — 0) = y'hh + 0) and the same for z(x). Then the conditions of selfadjointness for restrictions of Dh takes the form y'(—h) (—z(—h — 0) + z(—h + 0)) + y'(h) (—z(h — 0) + z(h + 0)) + + (y(—h — 0) — y(—h + 0)) z'(—h) + (y(h — 0) — y(h + 0)) ^(h) = 0, where y'(—h) = y'(—h ± 0), y'(h) = y'(h ± 0). Let additionally

(

⁽y ^(—h + ^{0) —} y ^{(—h — 0)) (} y ^(h + ^{0) —} y ^{(h — 0))}

A =        y^-fa

J    {^b 21 b 22j \ y ^(h) ) ■

The symmetry of the matrix B =

^ ^b 11 ^b 12 ^

b 21 b 22

is equivalent to the selfadjointness of the

corresponding restriction. If one considers y(x) under conditions (11) as a generalized

function (distribution), then y"(x) = y Cl (x) + (b_n y ' ( — h) + b i2 y '(hy)6'(x + h) + (b 2i y ' ( — h) + b ₂₂ y ' (h))5 ' (x — h) , where f Cl (x) = f '' (x) if f '' (x) exists in the classical sense and f Cl (x) = 0 in the opposite case. Then the corresponding extension D _h of D _h can be re-written as

D h y (x) = — y Cl (x) = —y '' (x) + (b ii y ' ( — h) + b_n y ' (h))5 ' (x + h) + + ^(b 21 ^y ' ^{( — h)} + ^b 22 ^y ' ^(h))b ' ^{(x — h)} ■

Let us choose a matrix B such that for every positive h the functions

e αx

Ф h (x)

e - αh

e - αx

+ e ^ax )

e αh

-

e - αh

e - αx

x ≤ - h,

| x | <  h, ^ h ^(x)

x ≥ h,

eβx, e-eh(—e-ex + eex)

e eh । e - eh

_- e - βx _,

x ≤ - h, | x | < h, x ≥ h

would be eigenfunctions of the operator D _h . Then

b 22 = b 11

b 21 ⁼ b 12

1              ,              1

a(1 — e - 2 ah ) ⁺ в (1 + e ^{-2 eh} )

1                     1

a(1 — e - 2 ah ) — в (1 + e - 2 eh )

Note that

h

У ♦ h ixidx =

- h

2e - ah

, so in the sense of distributions α

lim фh(x) = фo(x)--5(x), h→+0               α

where ф ₀ (x) = e ^{a | x |} , therefore in this case the limit generates a new boundary problem, that (maybe!) directly involves 5(x) .

The extension of D _h corresponding to (13) will be denote by D _h . Then (see (12))

_nf      ( _d ' (x — h) — f(x + h))(y ' ( — h) — y ' (h))

= —y (x>+             a(1 — e-2ah),

(f(x + h) + d'(x — h))(y'(—h) + y '(h))

—               в (1 + e-2eh)

It is unclear how to treat a limit pass by h ч 0 in the latter expression: the domain of D_h depends on h and the eigenfunction ф _h (x) does not converge to any function in L ² ( R ) . In the next section we consider some different approaches to this problem.

3.    A Limit Pass to One-Point Interaction: 3.1.    A Traditional Approach

In this Subsection we describe a suitable expression for the resolvent of D_h for a negative number — y ² , Y > a , Y > в and estimate the resolvent behavior for h ^ 0 .

Both operators D h and D reg are restrictions of D ^∗ . Moreover (compare Conditions (10) and (11)), y(t) E D _h П D reg if and only if y(t) E W ^{2 , 2} ( R ) and y ‘ (—h) = y ‘ (h) = 0 . Using this reasoning and (9) one can proves (see [2] for details) that (y ² I + D _h ) ^-1 f (t) =

+ “                    I ^ф h ^{(т)G(t —}

(j ^{f (т )G(t — т)dT —} (————

+

-∞

+ ^

J ^ h (T)G(t —

-∞

т )dT + “

-----У f (t)s h (t)dt+

-∞

θ h

т )dT + “

----- У f (t)w h (t)dt )^ +

-∞

^{+ (}Y ²

^^(t)     ! f⁽t)s _h (t^dt + —

— a ² )n h J                  (y ²

+ ^

.. / f ⁽ⁱ⁾w h (t>^dt) •

-∞

-∞

where and

S h (t)

' e^Y t sinh(Yh)

Y e Yh cosh(Yt)

--•

γ e Yt sinh(Yh)

, γ

n h = ₂ ^{sinh(Yh) γ}

•

t <  —h,

1 t | h (t)

t > h,

' e^Y t cosh(Yh)

,

Y .

e ^Yh sinh(Yt)

γ e Yt cosh(Yh)

— ^γ

t <  —h,

I t l

,

t >  h

_e    2 CQ^sh(Y^h)

h _γ

•

e-a X^h a + y e ^{—( e} + ^Y ) ^{h e} + Y

+

+

e-fa+^h Y sinh(ah) e -^+Eih Y cosh(eh)

•

•

( sinh(a + y)h   sinh(Y t   (a + Y) +

( sinh(e + Y )h t   ^(e + Y)

— a

⁽Y — ^a)

sinh(Y — в )h 1

(Y - в)    J '

Remark 1. Formulae (16), (17), (18) (19) show that al spectrum of D_h , except points — a ² and — в ² , is non negative.

In [2] the following equalities were proved lim Hh(t) • / f(t)sh(t)dt^ =0, h^o        J

-∞ for two

+∞ lim(Y2I + Dh)-1f (t) = [ f (t)G(t - т)dT + h→0

+ ∞  ^-∞                                 (21)

,2y ² G(t) Sgn(t) f                   \ \

(    (Y - в )     J f (t)G(t)^Sgn(t)dt)-

-∞

Thus, the strong limit s-lim(Y21+Dh)-1 is a one-dimensional perturbation of the resolvent for Dreg (see (9)). If f (t) is even, then (9) and (21) bring lim(72I + DDh)-1f (t) = (y2I + h→0

D _reg ) ^-1 f ( t ) but D _reg has not a point spectrum. Thus, the operator-limit lost the eigenvalue _γ 2 _- ¹ _α 2 and the corresponding even eigen-function.

Remark 2. The function ^ 0 (t)    = e ^{e | t |} Sgn (t) is an eigenfunction for

lim(Y ² 1 + D h ) h → 0

¹ corresponding to the eigenvalue ⁽ Y ²

-

. The unbounded operator

P ^{2 )}

(s- lim h ,, (- ² 1 + D h ) ^     — y ² 1 is a selfadjoint restriction of D O (see (2) and (3))

corresponding to the boundary conditions

y ‘ ( — 0) = y ‘ (+0), — в (y(+0) — y( — 0)) = y ‘ ( — 0) + y ‘ (+0),             (22)

that is a particular case of (4) with a = 0 .

Proof. The statement concerning ^ ₀ (t) can be checked directly, so it is enough to show that

(21) brings (22) and viceversa. Let w (t) = — ---— (2YG(t) — e

Y ² — p ²

^{e | t |})Sgn(t) , f (t) E L ² ( R ) ,

+ ∞

+ ∞

x(t) = f f ( t )G(t — t )dT + y (в + Y)w(t) / f (t)G(t) Sgn (t)dt . Then w(t) is continuous

-∞

-∞ and has an absolutely continuous derivative: w‘(t) = — ^

Ye ^{- Y | t |} — ве ^-

Y ² — в ²

β | t |

— \, so x ‘ (0) = 0 .

Thus, x(t) satisfies (22). Now let y (t) E D ( D q ) and satisfy (22). One need to prove that there is f (t) E L ² ( R ) such that lim(Y ² I + D _h ) ^-1 f (t) = y(t) and (D O + y ² I)y(t) = f (t) . h → 0

Let y(t) = y (t) +

y (+0) — y ( — 0)

^ 0 (t) for t = 0 and y(0) = —— в^{) +} y⁽⁺^ . Then y(t)

is absolutely continuous function, its derivative is absolutely continuous too and due to

(22) y ‘ (0) = 0 . Put f (t) = (y ‘‘ (t) + y ² y(t)) — ⁽y⁽⁺⁰⁾— y ⁽ 20^))(Y ----— ^ o (t) . Note that

y(t) E D(D _reg ) , so У (y ‘‘ (T) + Y ² у(т )) G(t — т)dT = y(t) . The rest is trivial.

-∞

□

• 3.2.    An Extension on a Larger Space

+ ∞

Let us consider the term ф _h (t) • ^ f (t)s _h (t)dt for an arbitrary function f (t) E

-∞

L ² ( R ) continuous at zero and find its limit in point-wise sense. If t ₀ = 0 , then

+ ^

lim ф h (t o ) • f f (t)s h (t)dt = lim e

-

h ^ 0         J                h ^ 0

-∞ a|t0| • У f (t)sh(t)dt = 0, but

-∞

The function

lim ф h (0) • I f (t)s h (t)dt = h -⁰            J

-∞

- / f (t)e ^{- Y | t |} dt + — f (0) . α             γα

-∞

l(t) = |

0,

1,

if t = 0 , if t = 0 .

has no sense as an element of L ² ( R ) , but can

be a “legal” element in a larger space. Let

Mt) = |

t — 12,    if t — 0, t + 2,    if t > 0.

Then i(t) G L 0 ( R ) and | i(t) | = 1 . Let us introduce the orthoprojection (P _o g)(t) :

(P o g )(t) = g(0)i(t),   g(t) G L ²^ ( R ).

Note that for any g (t) G L ²0 ( R ) :

II( I - P o )g(t )|| L^ ( R ) = l|g(t )llL2 ( R ) .

Let us introduce the operator A h (compare with (16)): L ² ( R ) П C ( R ) ^ L ² ₀ ( R ) ,

⁽ A h f ^)(t) =

+

+ ^

j f (r)G(t —

-

\

+ ^

j' ^ h (т)G(t

-∞

∞

т )dT — (

f ф h (т)G(t

-∞

η h

— r )dr + ^

-------У f (t)s h (t)dt+

-∞

θ h

— т )dr + ^

-------У f (t)w h (t)dt^   +

-∞

+ 1 ( 2 h^ 2Л--- / ^{f (t)}sh^(t)dt + 1 (Y ² — a ²) n h J

-∞

^ h (t)

( y ² — в Mh

У f (t)W h (t)dt j .

-∞

Note that for any f (t) G L ² ( R ) П C ( R ) the corresponding function (A _h f )(t) is continuous at zero, so (27), evenness of G(t) (see (8)) and oddness of ^ _h (t) bring the representation

Л

+ m

P o (A h f)(t) =   У f (r)G(r)dr

+^         \

• ⁺ / 2 ^^A   / ^f ^sh ^(t)dt|

• (Y² — a²)n h J               I

  -∞

—

f ф h (т)G(r)dr + ^

I f (t)s h (t)dt+

∞

η h

-∞

l(t) •

Our goal is to find the strong limit s - lim A h . Due to (26) lim (I — P ₀ )(A h f )(t) coincides h ^ +0                 h ^ +0

with lim (y ² I + D h ) ^-1 f (t) in the norm topology of the space L ² ( R ) , so (21) brings (note h ^ +0

that P ₀ G(t) Sgn (t) = 0 )

+ ^

,lim (I — Po)(Ahf)(t) = (I — Pq) / f (т)G(t — т)dT+ h^«-®

(+^\

2y ² G(t)Sgn(t)

----7-----м---- / ^{f (t)G(t)} Sg^n(t)dt •

(y — e)     J/

-∞

Simultaneously (20), (23), (25) and (28) bring lim Po(Ah f )(t) = Pq / f (t)G(t — т)dт+ h^0

+    ^{—7 2}

+ I (y ² — a ² )

-

-∞

+m у f (t)G(t)dt +

-∞

-

1?f⁽⁰⁾ I ^l(t) • _a 2 )

Let A q = s - lim A h . Then due to (29) and (30) h ^ +0

+ ^                            + ^

(A o f )(t) =   [ f (т)G(t — T)dT + a^GWSgnW ( f _{( t )}G_{( t )} Sgn_{( t )}dt+

J                       ⁽Y^{— e})     J

-∞

-∞

+

\ (y ² — a ² )

-

+ ^

у ^{f (t)G(t)dt} + (y

-∞

-

f⁽⁰⁾ I ^l(t), a ² )

where f (t) E L ² ( R ) П C ( R ) and (A _o f )(t) E L^ ( R ) . The space L ² ( R ) П C ( R ) has the natural dense embedding in the space L ² 0 ( R ) . Thanks to this observation one can introduce in L ² 0 ( R ) the operator A _o that initially was defined on L ² ( R ) П C ( R ) C L ² 0 ( R ) as in (31) and is extended on whole L ² 0 ( R ) by continuity. In particular, if £ _n (t) = e ^{-( nt )} , then

л

л

(Aoi)(t) = lim (Aq(n)(t) = n^^            (y 2

-

a ² )^l(t),

i.e. i(t) is an eigenfunction of A _o .

Note that Ao is not a selfadjoint operator. The latter contradicts the standard frame of Quantum Mechanics (see, for instance, [11]), so we need to construct a larger space where Ao can be extended to a selfadjoint operator. Let us recall Observation (14). The latter indicates that 5(t) is a natural candidate to be include in a new larger space. Let L be the linear span of L2 (R) П C(R) and 5(t). One can introduce on L a natural partial inner product [•, •]: [x(t),5(t)] = x(0), [x(t),y(t)] = / x(tMt)dt, where x(t),y(t) E L2(R). The -∞ inner product [5(t),5(t)] does not defined yet. Let [5(t),5(t)] = q, where q is some real

2n

.

number. Then [5(t) — т^ п (t), ^(t) — т^ п (t)] = q — 2т + т ²----, where т E R , £ _n (t) = e ^{( nt )}

2n

This yields [5(t) — T^ n (t), 5 ( t ) — T£ n (t)]L = 2 n = q-- -=o, so the latter is negative if n is big

—     <2n enough. Thus, the quadratic form [x, x] is indefinite on L for any q, so L can be consider as a space with indefinite metric. Notions and results concerning spaces with indefinite metric one can find in [12]. For simplicity we put q = 0, so mm = o,

[x(t),5(t)] =х(0),

∞

^[x(t),y^(t)] = У ^x(t) y ^(t)dt ,

-∞

where x(t),y(t) E L 2 ( R ) . Note that the choice q = 0 is compatible with the approach to Distribution Theory for discontinuous test functions given in [6]. L represents a prePontryagin space, where the number of negative squares for the corresponding quadratic form is one. This space can be completed till a Pontryagin space. There are different ways to introduce a Hilbert scalar pro duct, all these ways are topologically equivalent. Let us give one of them. The completion P of L is presented in the form P = L ² 0 ( R ) ©{ ^^(t) } $ e c , ||5(t) || = 1 and the space L ² 0 ( R ) conserves its Hilbert structure. Note that i(t) E L ^ ₀ ( R ) C P, | i(t) | = 1 and due to (33) [5, i] = 1, [i, i] = 0, L ² 0 ( R ) = L ² ( R ) © { gi(t) } _?e c . Our goal is to find an extension C ₀ of A ₀ in such a way that [C ₀ x, y] = [x, C ₀ y ] for all x,y E p. This property in the case of Pontryagin or Krein spaces (see [12]) is called J -selfadjointness. Evidently we need to find (C _o 5)(t) . Thus, due to (31) and (32)

+ ∞                    + ∞

^[C o ^{5(t),f (t)]} = ^[5(t), ⁽A o ^f)(t)] = ^f! ^{( t ) g ( t )dT} -              /f ^(t)G(t)dt +

J                  (y ² — a ²) J

-∞                  -∞

■          .. ЬЭД-f(t)]'

where f (t) E L^ ( R ) . Note that [(C _o 5)(t), 5(t)] cannot calculate using A _o , so put [(C _o 5)(t), 5(t)] = n with ambiguous n E R . Summarizing these facts we have

C o ⁵(t) =            ⁵(t) -             G(t) + ni(t)•                    (34)

Using Equality

+ ∞

/■ e ^{- a | T} l G( _t — t )dT =    e “'‘'   — ^2aG⁽t⁾ ,                      (35)

J                        (Y ² — a ² )    (7 ² — a ² )

-∞ and Representations (31), (32), (34) let us calculate Co(ф0(t) — 25(t)) with ф0 from (14):

С о (ф оИ — -5(t)) =     ¹ ₂ (ф оИ — ²5© + .(<)( ₂ °   —1— — ^).

a        (y2 — a2)         a             (y2 — a2) (y + a) a a 1      2n

If f——----—  --------) = 0 then (ф ₀ (t) — ²5(t)) is not an eigenfunction of C _o but it is a

(Y2 — a2) (y + a)   a                     a function adjoin to the eigenfunction i(t). This situation does not correspond to postulates of Quantum Mechanics [11], therefore

α

(7 ²

-

a ² ) (y + a)

-

2П\

—) = 0 , so α

(C o f )(t) = J f ( t )G(t - т)dT +

27 ²

GWSgnltl [ f (t)G(t) Sgn (t)dt+ ⁽7 - ^e)     J

-

∞

-

∞

+

- 7 ²

(7 ²

-

_a 2 )

У f (t)G(t)dt +

⁽7 ²

∞

-

_a 2 )

f (0) i(t) ,f (t) G L ² o ( R ),

C o ^(t) =

⁽7 ²

-

_a 2 )

^(t)

a ²

-

⁽7 ²

-

_a 2 )

G(t) +

2(7 ²

-

a ²

a ² )(7 + a)

l(t) •

Remark 3. Formulae (36) completely define J -selfadjoint operator C _o . By construction this operator has two eigenfunctions i(t) and (ф ₀ (t) — aa 5(t)) that correspond to the eigenvalue ( _Y 2 — _a 2 ) . Simultaneously Remark 2 shows that the function ^ ₀ (t) = e ^{- e | t |} Sgn (t) , ^ ₀ (t) = 0 is an eigenfunction for C _o corresponding to the eigenvalue ( _Y 2 — e 2 ) •

• 3.3.    A Pontryagin Space Effect

We use the terms “positive vector” , “neutral vector” , “non-negative subspace” , “maximal non-negative subspace” , etc., in the usual way: they are defined with respect to the sign of the quadratic form [ • , • ] (see [12]). Analogously by the symbol [ ± ] we denote the orthogonality of vectors or sets with respect to the inner product [ • , • ] • J -selfadjoint operators in Pontryagin spaces have a key property: any J -selfadjoint operator has at least one maximal non-positive invariant subspace. The dimension of maximal non-positive subspace coincides with the range of indefiniteness of the corresponding space.If L - is a maximal non-positive invariant subspace for a J -selfadjoint operator B then J -orthogonal subspace L — is non-negative, maximal and invariant for B . Note that if L - is a negative subspace then L — is positive one. In the case of Pontryagin space the inner product [ • , • ] restricted on a positive subspace is topologically equivalent to the original Hilbert scalar product. This brings an option to return completely to the postulates of Quantum

Mechanics where operators must act in Hilbert spaces. ∞

Due to (33) [ф o (t) — -5(t),ф o (t) — -5(t)] = / e ^{—2 a | t |} dt — αα

α

. α

-∞

Thus, ф0(t)5(t) is a negative element of p. Recall (36). One can consider the subspace α spanned by ф0(t) — 25(t) as a maximal negative subspace L- invariant with respect to Co.

Let N _a be the linear span of ф ₀ (t) — 2 5(t) and i(t) . Put

^(t) =^|(t)+1 [^|(t), ^ф o ^(t) — a 5^(t)] ^o ^(t) —

Then ^(t) G N _a , ф ₀ (t)--d(t)[ l ]^(t) , ^(t) is α

^- ад) = .(i) — ² (ад) — - ад) • (37) a J         3 \ a J

an eigenfunction for C _o and [^(t),^(t)] =

• 1= , i.e. N _a is an indefinite subspace. Since it is invariant for C _o , its orthogonal 3a  3a   a

complement N^ ] is also invariant for C _o , moreover it is positive. Put N = N^ ] . Then N can be described as follows

+ ∞

N = {f (t) : f (t) 6 LL( R ), f (0) = a / f (^)Ф o (^)d^}.                (38)

-∞

+ ∞

Note that for f (t),g(t) 6 N the representation [f (t),g(t)] = f f (t)g(t)dt takes place, so

-∞

N can be considered as a Hilbert space isometric to L2(R) in the evident sense. Note also (see Remark 2) that ^0(t) 6 N. If f(t) 6 L^(R), then it must be defined at zero. For u(t) 6 P, u(t) = f (t) + £5(t), f (t) 6 L0(R) we denote u (t)={Г

if t = 0 and f (t) is defined at t, if t = 0,

⋄⋄ so (see (24)) f (t) =f (t) + f (0)i(t). For an odd function f (t) evidently f (t) = f (t), i.e.

f (0) =0 for any odd function f (t) 6 L 0 ( R ).

Moreover, we assume that all functions from L ² ( R ) are simultaneously functions from L ^ ₀ ( R ) nullified at zero. With slight abuse of Notation (39) we shall use notations like ^■^      *

U (t) if u (t) is absolutely continuous function on R\{ 0 } ; here and below u ‘ (t) and

*

(u) (t) are treated as a derivatives of generalized functions. Thus, the symbol u' (t) is

⋄

⋄

defined as follows:

/^     о

U ‘ (t)= U '

⋄

^■^

(t) . By the same way the symbol u ^'' (t) is introduced.

Our aim now is a calculation of C ₀ 1 | N . First, let us find the range Rg(C ₀ | N ) of the

operator C ₀ | N Taking into account (36) for f (t) 6 N, (40) and Denotation (39)

we

have

+ ∞

⋄α f (t)+2 J f (t^o(t)dt • i(t)

-∞

⋄ г                  s +^

+ ^—-^^(t) Sgn (t) У f (t)G(t) Sgn (t)dt) +

,----------------*---------------- .

+ ∞

= J f ( t )G(t - T)dT +

-∞

-∞

+ ∞

α ²

• ^- ( _Y 2 - _a 2 ) J ^{f (t)G(t)dt} +

  -∞

+ ∞

^7 / ^{f (t)} Ф o ^(t)dt

-∞

Next, using Equality (35)) one can transform Equality (41) to

+ ∞                        + ∞

^⋄ α                      ⋄ α

C o I f (t)⁺2 / f (t)Ф o (t)dt • i(t) I =u (t)+^     u(t)ф o (t)dt • i(t)

-∞

-∞

with

+ ∞                  ₂            + ∞

• u(t) = f f ( t )G(t — т)dT +-- Y^G(t) Sgn (t) / f (t)G(t) Sgn(t)dt.

Y — e

-∞

-∞

Lemma 1. u(t) G Rg(C o | n ) if and only if simultaneously

the restrictions u(t) | ( -^ , o) , u ‘ (t) | ( -^ , o) , u(t) | (o , + ^ ) , and u ‘ (t) | ( ₀ , + ^ J are absolutely continuous ;

⋄⋄

^4^   ^^^^

u(t), u ' (t), u " (t) G L ( R ) ;

в (u( — 0) - u(+0)) = u ' ( — 0) + u ' (+0) ;

u ' ( — 0) = u ' (+0) ;

+ m

u(t) =u (t) + (2 у u(t)ф o (t)dt ) • i(t).

-∞

If u(t) G Rg(C o | N ) , then C o ¹

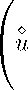
(t) + 2 / u(t)ф o (t)dt • i(t)

-∞

^             + m        ^

/----------*----------a f /------------*------------s

=-u''(t) + Y ² u(t) +2 j ( - U ‘‘ (t) + Y ² u(t)) (t)фo(t)dt • i(t),

-∞

Proof. The statement of Lemma 1 follows mainly from Remark 2, its proof and Formulae (41), (42), (43). Note that, generally speaking, u(t) contains a jump at zero, so u'(t) represents a generalized function with a singularity at zero, therefore instead of u′ the ⋄ function u' (t) was used, etc.