On a model of spontaneous symmetry breaking in quantum mechanics

We introduce in this paper a new mechanism for spontaneous symmetry breaking, with applications to molecular physics. We discuss it on one dimensional quantum problems. It is based on nontrivial boundary conditions which we describe as an “entanglement of boundary conditions” . The motivation for our proposal is on the study of symmetric potentials, under parity, where the stable quantum ground state is not symmetric, but it is right or left-handed. This situation occurs in many molecules with symmetric configurations of the nuclei of the atoms, where the ground state is right or left-handed. Moreover, the ground state is even not an eigenstate of the Hamiltonian. A typical example is the molecule NH3. Its quantum potential contains two symmetric attractive minima with a repulsive barrier between them. The ground state is non-degenerate and right or left-handed. The main point is that a non-degenerate eigenstate of a symmetric Hamiltonian must either be symmetric or antisymmetric under parity transformations. However, external perturbations change the phase of a symmetric or antisymmetric state giving rise to an unstable incoherent mixture of both. This effect is known as decoherence, see [1] and for a review [2]. On the other side, a state concentrated only on one side of the repulsive barrier would be stable under external perturbations, but not necessary an eigenstate. In that case it is unstable under the time evolution dictated by the Schrodinger equation. It would evolve from a right-handed to a left-handed state and vice versa, since it is not an eigenstate, becoming unstable after a period of time. Nevertheless, if the repulsive barrier is high enough this scenario occurs after so large time that approximately the state of the molecule is concentrated on the right or left side of the repulsive barrier with a very large decaying process. This argument explains the existence of right or lefthanded states in nature. In this paper we present a nonlocal interaction described by an entanglement of boundary conditions such that the corresponding symmetric Hamiltonian, for a particular value of the parameters describing the interaction, has a degenerate ground state. It is a linear combination of a right and a left-handed eigenstate. In addition, when we consider the phenomenon of decoherence the only stable eigenstate under external fluctuations corresponds to the left-handed or right-handed states. In distinction to our previous argument the stable ground state is now an exact eigenstate. So, our proposal fulfils both stability criteria. It is stable under external perturbations, since it is a left or right-handed state concentrated on one side of the barrier and stable under time evolution, since it is an eigenstate of the Hamiltonian. Our model describes the barrier in terms of the Dirac delta distribution, more precisely in terms of the derivative of it. The use of the Dirac delta distribution has been used with success in order to describe approximate potentials, see [3–11]. In our proposal the potential is modeled by two derivatives of the Dirac delta separated a distance 2h among them. The coefficients of each derivative of the delta depends on the boundary condition on the wave function at the other derivative of the delta. It is an entanglement of boundary conditions. The Hamiltonian we introduce is then symmetric under parity transformations and self-adjoint. Its ground state is an exact eigenstate concentrated on one side of the repulsive barrier. It is an interesting case of spontaneous symmetry breaking. The mathematical approach we will follow in our construction is a method of selfadjoint extensions of a symmetric operator.

Section 1 contains some known results concerning singular potentials in terms of the delta function and a small discursion on the subject. In particular, we mention a Hamiltonian whose ground state is degenerate, with two eigenfunctions, nevertheless, there is no symmetry breaking in this case. Further, in Section 2 and 3 we present the key contribution of the paper by introducing local and non-local potentials and discuss their quantum properties. In particular, the existence of spontaneous symmetry breaking is demonstrated in Section 2. In Section 3 we show that within a Hilbert space approach a spontaneous symmetry breaking disappears if h ^ 0 . Finally, we give our closing remarks in Section 4.

1.    Preliminary Remarks

Let us consider a well known case of a boundary value problem at the unique interior point coinciding with the origin. So, let D = —d2 • /dx2 be the differential operator on the set             D(D) = {y(x)| У(x),y‘(x).y"(x) e L2(R), У(0) = y‘(0) =0}.

Its adjoint one D ^∗ is the differential operator on the set

^{D ( D} * ) = ^{ y ^{( x ) |} y^(x),y ^{, (x),}y "^{( x )} | k + ^e L ^{2 ( R} + ), y (x),y ^{, (} x),y "^{( x )} | _R - ^e L ^{2 ( R} — ^{) }} .

where R ₊ = { x | x >  0 } and R _— = { x | x <  0 } .

For any selfadjoint extension D of D the relation D ⊂ D ^∗ holds. Thus, D ⊂ D ⊂ D ^∗ and any extension of D can be treated as a restriction of D ^∗ . Direct calculations bring (D * y, z) = - y ' ( - 0)z( - 0) + y ‘ (+0)z(+0) + y( - 0)z ' ( - 0) - y (+0)z ' (+0) + (y, D * z) .

The latter yields y'(-0)z(-0) - y‘(+0)z(+0) - y(-0)z'(-0) + y(+0)z'(+0) = 0           (1)

as a condition for the self-adjointness of the corresponding restriction. Since here boundary values form a four-dimensional space, any selfadjoint restriction can be given by two linear homogenous equations. In particular, the conditions (the same for y and z ) y ( - 0) = y(+0) and ^{y (+} 0(_O) y ⁽⁰⁾ = 2c = const are suitable. Under these conditions the first derivative of y (t) has a jump at zero. Therefore the second one treated as a distribution has a singularity like the delta-function and the corresponding extension D accepts a natural representation Dy(x) = - y"(x) + 2c • y(0)5(x) = - y"(x) + 2c • y(x)5(x) . For c <  0 the operator D has the negative eigenvalue A = - c ² and the corresponding eigenfunction y (t) = e ^c|x| . These facts are well known (see the monograph [12]). In the same book one can find a study on singular potentials like shifted delta functions or their first derivative in finitely many points, but this study touches only local boundary conditions.

The present work deals with a generalization of the described above scheme for a nonlocal boundary problem at two points - h, h and a behavior of the corresponding operator with two eigenfunctions if h ^ 0 . We show that the process h ^ 0 eliminates one of these eigenfunctions.

As it is well known, even for the one-point problem there are some selfadjoint extensions with one or two negative eigenvalues wich involve naturally not only the deltafunction but its first derivative: the boundary conditions ( a > 0, в > 0 )

afy ⁽ + ⁰⁾ + y ^{( - 0)}) = ( ^- y ^{, (} + ⁰⁾ + y ^{, ( - 0)}) . ^e(y ⁽ + ^{0) -} y ^{( - 0)}) = ^- (y ‘ ⁽⁺⁰⁾ + y ^{, ( - 0)}) .

• —0                                       +^o

2.    Basic Results 2.1.    General Setting

where J ( | y(x) | ² + | y(x) ‘ | ² + | y(x)" | ² )dx + J ( | y(x) | ² + | y(x) ‘ | ² + | y(x)" | ² )dx <  to , satisfy — oc                                      +0

Conditions (1), so the corresponding extension is selfadjoint. This case was analyzed in [13]. The extension D under discussion has two eigenvalues - a ² and - в ² , their corresponding eigenfunctions are e ^—a|x| and Sgn (x)e ^—e|x| respectively, Sgn (x) = 1 for x > 0 and Sgn (x) = - 1 for x < 0 , D is the selfadjoint Hamiltonian with Representation

Dy(x) = - y (x) - в • 5 (x) (y ( - 0) + y (+0)) - a • 5(x) (y( - 0) + y(+0)).

Our principal interest leads to the case a = в . Indeed, the latter yields that - a ² is the unique negative eigenvalue and has two non symmetric eigenfunctions y i (x) =

(1 — Sgn (x))e ^ax and y ₂ (x) = (1 + Sgn (x))e ^-ax . But still, the case under discussion cannot be treated as a model giving rise to a spontaneous symmetry breaking. Indeed, this case must be considered as a non transitable barrier because Conditions (2) yield a • y ( — 0) = y ' ( — 0) and a • y(+0) = — y ' (+0) , so waves on R _- and R ₊ are independent.

If the differential operator D = — d ² • /dx ² acts on the real line R with domain

D(D) = {y(x)| y^Yy‘(x),y‘‘(x) e L2(R), y(—h) = y,(—h) = y(h) = y,(h) = 0}, then for the adjoint operator D∗ we have

D(D*) = ^y(x)| y(x),y'(x) are absolutely continuous on (—to, —h) U (—h, h) U (h, to), y(x) e L2(R), y‘(x)l(.-^,-h),y‘‘(x)l(.-^,-h) e L2 ((—TO, —h)), y"(x)|(-h,h) e L2((—h,h)), y'(x i , л, v , y"i x i (л, x e L2((h, to))} and      (D*y, z) — (y, D*z) = —y'(—h — 0)z(—h — 0) + y (—h + 0)z(—h + 0) —

• — y ' (h — 0)z(h — 0) + y ' (h + 0)z(h + 0) + y( — h — 0)z'( — h — 0) — — y ( — h + 0)z'( — h + 0) + y (h — 0)z'(h — 0) — y(h + 0)z'(h + 0).

The latter means that a selfadjointness for a restriction of D ^∗ holds if and only if the set of corresponding boundary conditions is minimal (four equations only) and yields

— y ' ( — h — 0)z( — h — 0) + y ' ( — h + 0)z( — h + 0) —

— y ' (h — 0)z(h — 0) + y ' (h + 0)z(h + 0) + +y( — h — 0)z'( — h — 0) — y( — h + 0)z'( — h + 0)+ +y(h — 0)z'(h — 0) — y (h + 0)z'(h + 0) = 0.

Designing selfadjoint restrictions of D ^∗ we can, in particular, assume

y(—h — 0) = y(—h + 0), y(h — 0) = y(h + 0), that means the continuity of y (and, of course, z). Then condition (4) takes the form

(y ' ( — h + 0) — y ' ( — h — 0))z( — h) + (y ' (h + 0) — y ' (h — 0))z(h) — — y ( — h)(z'( — h + 0) — z'( — h — 0)) — y(h)(z'(h + 0) — z'(h — 0)) = 0.

An essential part of this case (including an entanglement of boundary conditions) was analyzed in [14]. In particular, it can be shown that under some restrictions and h ^ 0 conditions (5), (6) convert to conditions (2). Next, it is well known how to calculate the resolvent for the selfadjoit differential operator D reg given by the formal differential expression D reg = — d ² • /dt , acting on the real line R and having the domain D (D _reg ) = { y(t) | y(t),y ' (t),y '' (t) e L ² ( R ) } . Let G(t) = e----. Then for every z(t) e L ² ( R ) and y > 0 2y

+ ^

(y ² 1 + D reg ) ^-1 z(t) = У z(t )G(t — T)dT.

-∞

Note that D _reg represents the restriction of D ^∗ conditions

that (see (4)) corresponds to the boundary

y^(—h — 0) — y^(— h + 0), y'( - h — 0) — y'( — h + 0),

У(h — 0) — y(h + 0), У ' (h — 0) — y ' (h + 0).

• 2.2.    An Entanglement of Boundary Conditions for the Continuous First Derivative

Now, we will drop out conditions (5). Alternatively, we assume that both derivatives y′ and z′ are continuous at points -h and h. Then condition (4) converts to y'(—h) (—z(—h — 0) + z(—h + 0)) + y'(h) (—z(h — 0) + z(h + 0)) + + (y(—h — 0) — y(—h + 0)) x4—h) + (y(h — 0) — y(h + 0)) x4h) — 0

Designing the selfadjoint restrictions of D ^∗ we assume that

(b ii  b^A yy ' ^{( — h )}A _— f^{(y(—h + 0) — y ( — h — 0))}A

\^b 21   ^b 22/ XVW /     \ ^{( y ( h + 0) — y ( h — 0))} )

The planning restriction will be selfadjoint if and only if the matrix

B —

Ab 11 ^b 12 ^ b 21 b 22

is symmetric. Let a function y(x) satisfy Conditions (9). If we consider it as a generalized function (distribution), then y''(x) — y^l(x) + (bii y'(—h) + bi2 y '(h))#'(x + h) + (b2i y'(—h) + b22y'(h))^'(x — h), where fCl(x)

0, f '(x),

if f (x) has no sense in the classical approach; in the opposite case.

Using this notation, the extension D h of the operator D can be presented as

D ) h y(x) — — V ' (x) + (b ii y ( — h) + b i2 y' (h))# ' (x + h)+ ^{+ ( b} 21 У ' ^{( — h ) + b} 22 У ' ^{( h ))} # ' ^{( x — h )} .

This is the image of the Hamiltonian, for a suitable matrix B which we will determine below, of our proposal acting on a wave function y(x) for the quantum mechanical problem discussed in the introduction based on the molecular structure of NH 3. When b 11 — b ₂₂ and b ₁₂ — b ₂ 1 it is invariant under parity transformations, in fact, if u(x) is an eigenfunction so is u( — x) with the same eigenvalue.

Let a matrix B be such that for every positive h the function

Ф h (x) —

e αx

x ≤

^{— h ;}

e - αh

e - αx

+ e ^ax )

e ^αh

- e ^-αh

e - αx

x G ( — h, h);

x >  h;

represents an eigenfunction of the operator Dh . Direct calculations show that the h                  -αh corresponding eigenvalue is A — —a2. For any h the equality J фh(x)dx — — 2ea— holds,

-h so in terms of distributions lim фh (x) = f0(x) h→+0

— a 5(x) with f ₀ (x) = e ^a|x|

therefore the

limit can generate (maybe) a new boundary problem, that directly involves 5(x) , but it is impossible within the frame of L ² ( R ) . Next, using (9) and (11) we have

2                              2

1 - e - 2 ah = ^a ^ ^(b 11 - ^b 12 )’   1 _— e - 2 ah = ^a "  ⁽ b ²¹ - b ^{22 ) .}

B is symmetric and therefore the last system yields b 11 = b ₂₂ and b ₂^ = b ₁₂ .

B is not yet completely determined, so we can assume that D h has an eigenvalue ц = — в ² . If Ц = a and an eigenfunction ^ _h (x) corresponds to ц , then ф _h (x) and ^ h (x) are orthogonal. The latter would be fulfilled if ^ h (x) is odd. We put

^ h (x) =

eβx, e-eh (—e-ex + eex) eeh । e-eh

-e- ^ ,

x < — h;

x G ( — h, h);

x >  h.

Due to (12) we have — 1+e-2eh = в • e eh • (b11 + b12), — 1+e-2eh = в • e eh • (b21 + b22)• So b22 = b11

b ₂₁ = b ₁₂

1              ,1

a(1 — e ^-2“^h ) ⁺ в (1 + e ^-2eh )

a(1 — e - ²“^h ) — в (1 + e - 2 eh )

The locality of this interaction is equivalent to the condition b12 = b21 = 0. Thus, 11

a(1 — e - ²“^h ) = в(1 + e - 2 eh )^.

Evidently, в < в ' (1 + e - 2 ^eh ) = a • (1 — e ^-2ah ) < a . This means that the local interaction determines the non-degenerate ground state given by (11).

Our principal interest corresponds to the case a = в . Due to (13)

b 11

— 2       b        2e ^-2ah

a(1 — e ^-4ah )’ ¹² = a(1 — e ^-4ah )^.

The latter brings b ₁₂ > 0 , so we have an entanglement of boundary conditions. Furthermore, any ground state is a linear combination of (11) and (12) and can be asymmetric. In particular, ф _h + ^ _h is an eigenstate with the wave function concentrated on x <  h and ф _h — ^ _h is an eigenstate with the wave function concentrate on x > — h . In addition, when we consider the phenomenon of decoherence the only stable eigenstate under external fluctuations corresponds to ф _h + ^ _h or ф _h — ^ _h , the left handed or right handed ground states. In distinction to what occurs in the argument presented in the introduction, the stable state is an exact eigenfunction and hence it is also stable under the time evolution. Consequently, the entanglement of boundary conditions gives rise to spontaneous symmetry breaking of the parity symmetry of the Hamiltonian (10).

Note that b 11 ,b ₁₂ ^ 0 and Ьц ^ 0 by a ^ to , so for a big enough the violation of locality in (8) is relatively small. In the opposite case, if a ^ 0 , then b 11 ,b ₁₂ ^ to and

Ьц ^ — 1 , so in this case the entanglement between the points — h and h is quite strong. The same effect takes place if a is a constant but h ^ 0 , that is natural.

The extension of D that corresponds to (13) will be denote by D h . In the case of D h Expression (10) can be re-written as D _h y(x) = — y ‘‘ (x) + (54x — h) — d ‘ (x + h))(y ‘ ( — h) — y ‘ (h)) (5'(x + h) + 5'(x — h))(y ‘ ( — h) + y'(h)) _

a(1 — e-2ah)                                в(1 + e-2eh)              . From the strict point of view the latter expression has no limit if h ^ 0 because the domain of Dh depends on h and the eigenfunction фh (x) does not converge to any function in L2(R).

3.    Limit Pass: a Hilbert Space Approach

Since the operator Dh is unbounded, the limit of Dh will be substituted by the limit of its resolvent. Let us calculate the resolvent of Dh for a fixed real point —y2, Y > a, Y > в and investigate its behavior for h ^ 0, the calculation will be based on Formula (7). Both operators Dh and Dreg are restrictions of D∗ , therefore for their domains Conditions (3) are fulfilled. Moreover, if y(t) E Dh П Dreg then Conditions (8) and (9) are fulfilled simultaneously, y(t) as absolutely continuous and y ‘(—h) = y'(h) = 0                                   (15)

vice versa, if Conditions (15) hold, then y (t) E D (D _reg ) ^^ y (t) E D (D h ) .

+ ^

Let z(t) E L ² ( R ) and y(t) = У z(т)G(t — т )dт . Then y(t) E D (D _reg ) and y ‘ (t) = — y •

-∞

+ ^

J z(т)G(t — т ) Sgn (t — т )dт . Let z(t) be such that

-∞

+ ^

У z(т)G( — h — т ) Sgn ( — h

-∞

+ ^

-

т )dт = У z(т)G(h

— т ) Sgn (h — т )dт = 0 .

-∞

Then Conditions (15) are fulfilled, so y(t) E D (D _reg ) П D (D _h ) and due to (7) (y ² I + D h )y(t) = (y ² 1 + D reg )y(t) = z(t) . Thus,

+ ^

(y ² 1 + D h ) ^-1 z(t) = y(t) = У z(т)G(t — т )dт .

-∞

Let us introduce some notations. We put sh(t) = G(—h — t) Sgn (—h — t) — G(h — t) Sgn (h — t), wh(t) = G(—h — t) Sgn (—h — t) + G(h — t) Sgn (h — t),

Kh = {f (t) : f (t) E L2(R), f (t) ± Sh(t), f (t) ± wh(t)} and denote by Lh the linear span of фh(t) and ^h (t). Then (note that this decomposition is not orthogonal)

L ² ( R ) = K h +L h .                                (17)

Let n h = fS h (M (t)dt and ⁹ h = T W h (t)^ h (t)dt . Then for every f (t) G L ² ( R ) the

-∞                 -∞ decomposition (17) takes the form

f(t) = (f(t) - (^Ф    J f (tw + p j f (tM(t)dt))+

+ ^

+ ^

Thus (16),

-

-∞

+ ^

-∞

+ ^

+( — f f (tK^dt + ^ / f (t^W) . η _h                       θ _h

-∞

-∞

(y ² 1 + D h

+ ^

[ f (т)G(t — т)dT —

J ф h (т )G(t — т)dT + ^

-^------------------- f (t)s h (t)dt +

η h

-∞

+ ^

J r h ( t )G(t - т)dT + ^

-∞

θ h

\

-∞

+ ГО j f (t)wh(t)dt   J

+ (18)

-∞

+ ^

⁺ [ ( 2^ h^ L-- [ ^{f ( t )} sh ^{( t ) dt +}

1 (y ² — a ² )n h J

+ ^

/

■ / ^f(t^WM

.

-∞

A simple transformation gives " e ^Yt sinh(Yh)

-∞

s h ( t ) =

^{, γ} e ^Y h cosh(Yt)

, γ e Yt sinh(Yh)

,

t < — h;

I t | < h;

w h ( t )

γ

The direct calculation brings

t >  h;

' e^Y cosh(Yh)

,

Y e 7h sinh(Yt)

γ e Yt cosh(Yh)

,

t < — h;

I t | < h;

t >  h .

γ

nh = 2sinh(Yh) γ cosh(Yh)

O h = ²-------- ^γ

•

•

e - ( ^a+7 ) ^h a + y e ^-(e+7^{)h e} + Y

+

e ^-(a+7^)h Y sinh(ah) e ^-(e+7^)h

⁺ Y cosh(eh)

J sinh(a + y )h

|   ^(a + y )

J sinh(e + Y )h

I    ^{( e} + Y)

+

-

sinh(Y — a)h

(Y — a)  Г sinh(Y — в )h 1

(Y — в ) Г

so lim n h = — and lim ⁹ h = h -G            - -           ’ "

γα

h ^ G

Y ^{( e} + YУ

Our aim is to investigate the behavior of (y ² 1 + + ^

D h ) ¹ for h ^ 0 . Let us analyze the term

ф _h (t) • j f (tys _h (t)dt from (18). First, we have

-∞

и , и           - h Г 1          1         f sinh(2ah)    , \ i ^1/2

"Ф1 "L2(R) = e (a + sinh2(ah) "(   2a    + h) }   ’ и и e Yh f . . 2,         (sinh(2Yh)    , A 1 1/2

||^s h H l 2 ( R ) = Y^Y I ^sinh 2 ⁽ Y^{h )} + ---- 2---- ⁺ hYp •

Thus, lim ^h^L2(R) = to, lim |Ы^2(r) = 0, lim |Ш^2(r) • ||sh||l,2(r) = 2- = 0. Second, h^G                  h^G                h^G                           Y for every fixed f (t) G L2(R) we have

+ ^

- h

У f (t)s h (t)dt <  I f (t)s h (t)dt +

+ h /

f (t)sh h (t)dt

+

-∞

∞

+

+ ^

+ I f (t')sh(t')dt <

+ h

1 / 2     _+h

1 / 2

- h

1 / 2

+

1 / 2

1 / 2

1 / 2

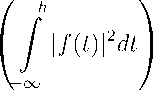
1 / 2

sinh(Yh) • e ⁷h Y V 27

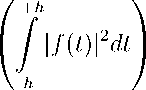
1 / 2

γh _h

γ

sinh(2Yh) 2Yh

,       / -^            \ 1/2

+ 1) + Ulf wU

Y 2 Y

+ h

+ h

Since lim f | f (t) | ² dt = 0 , estimation (20) and equalities (19) bring the equality lim ^h(t) • h > G -h                                                                                               h >G

+ ^

У f (t)s h (t)dt | = 0 . The latter brings the equality (the limit is treated in the sense of

-∞ norm topology)

+ ^

lim(Y ² 1 + D h^ f (t) = [ f (t )G(t - т ) dT - ^h ^ ^G                     J

+ ^

^- Y ^{( e} + Y) У

e - β | τ |

-∞

+ ^

Sgn (т)G(t — т)dT j f (t)G(t) Sgn(t)dt+

-∞                  -∞ f-e|tl Яд-п     +F

+ (Y _{( Y —} ^g ') J f (t)G(t) Sgn (i)di) .

-∞

As one can observe the operator-limit lost the eigenvalue _Y 2 - _a 2 and the corresponding even eigenfunction. This limit was taken in strong operator topology and the corresponding limit in norm operator topology does not exist at all. It seems that the operator-limit has some kind of escaping eigenfunction that cannot be detected within the space L ² ( R ) .

Closing Remarks

In this paper, we analyzed through a method of selfadjoint extensions for symmetric operators a new quantum interaction, realized as an interaction of the type of derivatives of two shifted Dirac distributions. These distributions, with adequate coefficients, are concentrated in two symmetric points h and — h respectively, ensuring the corresponding

Hamiltonian operator to be selfadjoint. We analyzed the boundary conditions which preserve the Hamiltonian, under parity transformations, and consider first those for which the interaction remains to be a local one. In this setting the discrete spectrum is constituted by an even or symmetric state and an odd or antisymmetric state (all of this under parity), with the ground state associated with the former of them. There exist also boundary conditions which imply a non-local interaction. We called it an entanglement of boundary conditions. In this case we obtained a degenerated ground state with the wave function concentrated on one side of the interaction zone, being zero on its complement. These are the left-handed and the right-handed states, and any linear combination of them remains an eigenstate with the same eigenvalue. However, when external perturbations on the wave function are taken into account, which inevitable occurs, the only stable states are just the left or the right-handed ones. The other eigenstates, because of the decoherence fact, rapidly become an incoherence mixture of even and odd states. An spontaneous symmetry breaking is then produced by the entanglement of boundary conditions It is interesting that this effect is obtained for a finite coupling constant term on the derivative of the Dirac distribution, in distinction to the case of a local interaction, where the only case in which we have spontaneous symmetry breaking corresponds to an infinitely high and thick barrier. If we visualize it in terms of a local Dirac interaction, the coupling of it must necessarily go to infinity. We applied the non-local interaction to give a qualitative description of the molecular structure of NH3. We compared our argument based on exact energy eigenstates to the well-established one, for which the left and the right-handed states are only nearly energy eigenstates. Finally, we showed that within a frame of Hilbert spaces the even eigenstates disappear if h → 0 .