On a new liquid filtration model

While preserving succession with the previous studies [1], the focus of researchers' attention for the recent years has come back to the positivity of operator semi-groups, and to physically significant models, arising from the certain applications for positive solutions of operator equations [2–4]. Indeed, as a rule, we mean the absence of physical sense when we receive negative or imaginary values of the variable concerned, which should be positive by sense: number of people, material volumes, amount of fluid, speed, pressure, market trends forecasting at economic processes simulation, population theory, fragmentation processes, linear transport theory, kinetic theory, birth and death rate-like systems, etc.

It should be noted that the line of papers describing a new liquid filtration model, the model of blood circulation in human lower extremities, is available for today. Let us enlarge on the paper in which it is represented. Namely, the paper [5] describes the mathematical model of blood circulation in human lower extremities, based on laws of motion (filtration) and viscous fluid preservation in heterogeneous medium:

—ДPi = Pi^p + q, i=1,2, (1) p d t dm where в = ——, Д, pi, ki, и are compressibility coefficients of the embedded media pore space dpi

(vascular network elasticity), laplacian operator, pressure, media permeability and fluid viscosity, respectively.

By the embedded media, the authors [5] mean the arterial medium and the venous medium. Their pore space is composed by vessels of various diameter, providing blood overflow: numerous arteries and numerous small capillaries, passing into larger veins. Speed of blood overflow in vascular beds is proportional to the pulse pressure, blood overflow unit volumes in vascular systems are preserved, specifically, due to capillary exchange between media. The model characteristics are their vascular conductivity and elasticity.

The authors of the aforementioned paper earlier offered a model of closed blood circulation in human brain tissues [6]

+-

• -β1∂S +∆S+=0;-β1∂S +∆S--2η1S-=0;(S±(x,t)=pa±pυ), ∂t∂

based on solid heterogeneous porous medium methods. Continuing such reasoning, we can draw some analogy of the concerned mathematical model of blood circulation in human lower extremities with the mathematical elastic-filtration hydraulic seam fracture model is emphasized

∂p

• - η  ( ∆ p ) = ∆ p , p ₂ = p - η ∆ p .

∂τ∂

The relatively large vessels (arterioles) should be considered as a sparse system of rather large fissures; and small capillaries, passing into larger veins, should be considered as a system of finely-porous units. Increase in total volume of fractures leads to decrease in units porosity (condition of pore volumes strain compatibility), which causes the media permeability value change. In totality of the aforementioned, we have an equation similar to the diffusivity equation, describing the elastic filtration mode.

The authors, V.I. Penkovsky and N.K. Korsakova obtained the time-periodic problem solution without initial conditions for the system of differential parabolic equations, corresponding to harmonic vibrations, determined by cardiac rhythm. They found analytical problem solutions, having considered the particular cases: 1) with permanent muscular tissue section area, proportional to specific flows and overflow values (gravity was absent); 2) at rigid mode of blood circulation in arterial and venous beds with the bent section function (zero arteriole elasticity). They provided the numerical solution of the one-dimensional problem, aligned with the results of analytical solutions.

Unlike the authors of the initial paper, for more exact study of the dynamics of process of blood circulation in human lower extremities, we plan considering the mathematical model in common case, without neglecting vascular elasticity and various vascular conductivity; in addition, the ambitious plan is to take into account the gravity further. Further, it will be also possible to analyze the model with regard of adding the following important physiological parameters: vessel resistance, volumetric blood flow, gas and nutrient metabolism, and to check the modified model against experimental data or realtime observations for efficiency confirmation.

There exist the sufficient number of the one-dimensional haemodynamics model modifications. Both earlier and existing models and the model to which this paper is dedicated, are based on real-time measurement data or physiological data close to them. Blood pulsation in veins, vascular wall resistance, speed and pressure in them, speed and pressure profiles, muscle pump performance speed, blood circulation volume, other parameters and haemodynamic significance indicators do not involve negative values. The mathematical apparatus for modelling systems using these characteristics, in their extraordinary majority as a result also involves non-negative (positive) solutions.

Let us consider the system arising from (1), assuming that arteries and veins have various elasticity and vascular conductivity:

_{- β 1} ∂ h a ₊ ∂ t

_{- β 2} ∂ h υ ₊ ∂ t

1 ∂ s ( z ) ∂ z

Г z dhha У

I S ⁽ z )       I = П 1 ( h a

L     дz J

1 ∂ s ( z ) ∂ z

- h _υ ),

I _z dhhv У

I s ( z )       I = П 2 ( h_a

L     dz J

- h _υ ),

dm h ^{d (} P a ^- P gz) + ^{1 d} I s ( z ) ^{d (} P a ^- P gz) I = ^a ( p dp_a      Э t        s ( z ) Э z L          Э z      J k 1 u ^a

-

dm ₂ ∂ ( p _υ - ρ gz ) dp _υ     ∂ t

1 ∂ +

s ( z ) ∂ z

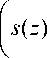
^{d (} P v ^- P gz) V   a

- dz     J    k1U

p _υ ),

- p _υ ),

Without regard of the vessel joint deformation condition, the system below is subject to linearization

dm i ^{d (} P a ^- P gz) + ¹ ( ^{d (} P a ^- P gz) ^ ^d ( s ₍ z) d (P a -P gz) ^ = ^a ₍ „ _ „ )

dpa Ә t qa I dz J Эz L dz J k1^ Pa PV dm 2 d( Pv - Pgz )х 1 | d( Pv - Pgz) 1 d I    Ә( Pv - pgz) ү  a

Ж    a t    ⁺ 7, L     d z    J a z L s ⁽-)     d z    J— k^^(P a ^{- P u} )

Let us take into account the transformation of media permeability value. Let us emphasize that the porosity change is low compared to initial values, and the permeability value varies significantly. Along with that, blood pulsations in veins are negligible compared to pulsations in arteries, so it is important to provide physiologically correct pressure drop between them as well. Taking the above into consideration, we will receive the following system:

' 1 d z?(Pa -Pgz) V a s^) dZ Is (z) dZ J ■ k^(Pa - Pu), dm2 ∂(pυ -ρgz)    α

∂ t

, dP u

= -    (pa - pυ), k1µ

Indices 1 and 2 will indicate the parameters in the environment of arteries and veins, respectively.

The, the modified model in initial designations will look as follows:

k i       a

U ^Л p a    LL^Pp a   p^U),

µµ dPu=a(n

• ^в 2 d t    ц ^{Pa P u} ).

Such model adaptation with the set limit and initial conditions, not inconsistent with reason, and setting the limited range of parameter values, safe for human body, reinforces the significance of positive solution methods development. Requires representation in the form of the Sobolev type equation. Claims further research in the issues of optimal positive decision management. Such solution may have no direct physiological analogy, but it can be used for numerical methods debugging and testing.

The research was carried out at the expense of the grant from the Russian Science Foundation no. 24-11-20037,

Bulletin of the South Ural State University Series “Mathematics. Mechanics. Physics” 2024, vol. 16, no. 3, pp. 45–49