On Borel's extension theorem for general Beurling classes of ultradifferentiable functions

Definition 1.1. An increasing continuous function ш : [0, го) ^ [0, го) is called a weight function if log t = o(ш(t)), t ^ го;

ш(t) = O(t); t ^ го;

^_ш (x) := w(e ^x ) is convex on [x o , го ).

∞

A weight function ш with J t ^{- 2} ш(t) dt <  го is called nonquasianalytic.

Denote by W ^ the set of all sequences Q = { ш _п } П=1 of weight functions with the folllowing property: for each n E N there exists a Cn > 0 such that

Ш n (t) + log(t + 1) 6 Ш n₊1 (t) + C n for t >  0.

By Wnq denote the set of all sequences Q = {wn}n=1 of nonquasianalytic weight functions шп. Without loss of generality we can assume that шn(t) 6 wn+1 (t) for t > 0 and n E N.

The Young conjugate y* : [0, го) ^ [0, го) of уш is defined by yL (у) := sup{xy - уш (x) : x > 0}.

For A E (0, го ) we define the space

E L ⁽ⁿ N ) ^:= J ^{f E} C “ ⁽ⁿ N ) ^{: | f} ^,1,V ^:= Sup sup ^f , ^ <  ^го| ,

(                                    aeNN kxk6A e(|a|)         J where nN := {x E RN : ||xk 6 A}, kxk : = max{|xj-| : 1 6 j 6 N} for x = (x1,...,xn) E ∂|α| f

RN , | a | := a 1 + ... + aN for a = (a x ,..., aN ) E NN , f ^{( a )} :=     ---- ro^p.

“          dxf ... ∂x _N

(c) 2007 D. A. Abanina

Next, for a weight sequence Q = { w n } n=i G W ^ we put

∞

E (Q) (n N ) := qE(n N );

n=1

E (q) ( R ^N ) := {f G C     N ) : f | _n N G E (_Q) (n N ) for each A > 0} .

The elements of E (q) ( R ^N ) are called Q -ultradifferentiable functions of Beurling type.

Let us introduce now the corresponding spaces of sequences of complex numbers:

E N := p = (da)a e N N G C N N

| d _α |

: W-Un := sup        < to S aeNN e(|a|)        J

and

∞ n . _ \ nN E(Q) : = I \ ®nn • n=1

It is clear that the restriction operator p : f G C“(RN) ^ (f(a)(0))aGNN acts from E(q)(RN) into E(N). If P is surjective, we will say that a version of Borel’s extension theorem holds for the space E(q)(RN) (for the original Borel’s extension theorem see [7]). For minimal Beurling class (wn = nw, w is nonquasianalytic and w(2t) = O(w(t)) as t ^ to) Meise and Taylor [8] have shown that E(q)(RN) admits a version of Borel’s extension theorem if and only if w is ∞ strong, i. e. there exists a C > 0 such that J t-2w(yt) dt 6 Cw(y) + C for y > 0. The case of 1

normal Beurling class, when Q = { q n w } n=i with q _n f q G (0, to ) and w is a nonquasianalytic almost subadditive weight function, has been studied by the author in [4]. In this case, p : E (q) ( R ^N ) ^ E^ ) is surjective iff w is slowly varying, i. e. t lim J( q = 1 .

The main result of the present article is the following theorem.

Theorem. Let Q = { w n } n=i G Wnq. Each of the following two conditions is sufficient for E (q) ( R ^N ) to admit a version of Borel’s extension theorem:

• (I)    for every n G N there exist m G N and C >  0 such that

  

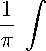
  ^w n ⁽ k € + NV) t ² + 1

  -∞

  
  

dt 6 w m ( k ^ + in k ) + C for ^ + in G C ^N ;

• (II)    for every n G N there exist m G N and C >  0 such that

w _n (2t) 6 w _m (t) + C for t >  0

and

∞

4 Г ^w n (yt) dt 6 W m (y) + C for y >  0.

nJ t² + 1

Suppose additionally that for each n G N there are m G N and C >  0 so that w_n(x + y) 6 w _m (x) + w _m (y) + C for x,y >  0 . If Borel’s extension theorem holds for E (q) ( R ^N ) for at least one N ∈ N , then

• (III)    for every n E N there exist m E N and C > 0 such that

2.    Criterion in terms of entire functions

∞

2 Г ^ « (yt) dt ^ ^ m (y) ₊ c for y >  о .

nJ t² + 1

This theorem generalizes the results of [8] and [4] mentioned above. It should be also noted that (II) implies (I).

The paper has five sections. In Section 2 we get a criterion of surjectivity of ρ in terms of entire functions. In Section 3, using the method of Meise and Taylor [8], we obtain sufficient conditions on Q E W^ under which E (_Q) (R ^N ) admits a version of Borel’s extension theorem. Necessary conditions are derived in Section 4 by the method of [8] and [1]. The last section consists of two new examples of Beurling classes. We show that Borel’s extension theorem holds for the first class and does not hold for the second one.

The author is grateful to professor Yu. F. Korobeinik for useful discussions.

Let Q = { ^ n }^ ! be in W ^ , and let the topology of E (q) ( R ⁿ ) (resp. E N) ) be given by the system of seminorms | · | ω _n ,n,N _{n ∈ N} (resp. by the normsystem | · | ω _n ,N _{n ∈ N} ).

For a weight function ш and a number A E (0, to ) we define the following space of entire functions

H-A(CN) ;= {f E H(CN) : kfk-AN := zsup e^g-(M) < ~j , where ||zk = max{|zj| : 1 6 j 6 N} for z = (zi,..., zn) E CN. Obviously, H,a(Cn) is a Banach space with the norm || • ||ш ,a,n. Next, for a weight sequence Q = {шп}П=1 E W^ we put

∞∞

H (Q) (C N ) := U H n ' )’ HN ) := U H- n ,o (C ^N ) • n=1                      n=1

Let H (q) ( c ⁿ ) (resp. HN) be equipped with the topology of in d H_-nn (C ^N ) (resp. in d H _{- n} ,o (C ^N ) ). Note that H^ ) and H (q) ( R ⁿ ) are (DFS ) -spaces.

By theorem 1 of [3], the Fourier–Laplace transform

F : ^ ^ b (z)= Цх e - i hx,^^

is a topological isomorphism from ( E (q) ( R ⁿ )) ^ onto H (q) ( c ⁿ ) . As usual, we denote by E ( the strong dual of a local convex space E .

A description of (ENy) _b is given by

Proposition 2.1. Let e_a, a E N ⁿ , be unit vectors in R N N , and Q = { ш _п } П=1 be in W ^ .

Then the Fourier–Laplace transform

F : ц ^ b (z) = У^ ц(еа)(-iz) ^a

α∈N0N is a topological isomorphism from (E(N) )b onto H^y

Here z ^a = z“ 1 ... zN N for z = (z 1 ,..., z n ) E C ^N and a = (a 1 ,..., aN ) E N ⁿ .

C Since the proof is very similar to that of [4], we omit it. It should be only pointed out that the proof is based on the following property of Q = {wn}n=i G W) derived in Lemma 1 of [3]: if Bn is determined by the condition wn(t) 6 Bnt for t > 1,                                   (2)

and C _n is determined by (1), then

^ ^ _n+1 (s) - G C (s) 6 - log s + log(B n e ^{C n +1} ) for all s> 0. B

Now we have a commutative diagram

(E(O)(RN))b ---- (E(N))b fI                         If

H CN ) — HN )

where p ⁰ is the conjugate operator of p . It is easily checked that F ◦ p ⁰ ◦ F ^{- 1} is the identity mapping acting from HN ) into H (q) ( C ⁿ ) .

Our main result in this section is

Theorem 2.2. Let Q = { ш _п } П=1 G W ) . Then the following assertions are equivalent:

• (i)    a version of Borel’s extension theorem holds for E (q) ( R ⁿ ) ;

• (ii)    for each set B C HN ) contained and bounded in H ^ _n ,n (C ^N ) for some n G N there exists an m G N such that B is contained and bounded in H^ m , o (C N ) ;

• (iii)    for each n G N there exist m G N and C >  0 such that

sup |f (z)к 6 C sup —„ |f(z)| ... ... for all f G HNy;(3)

zGcN e"m(kzk)       zGcN enkImzk+^n(kzk)(

• (iv)    for each n G N there exist m G N and C >  0 so that

|f(z)| 6 enkImzk+^n(kzk) for all z G CN, f G HN(4)

imply

|f (z)| 6 Ce“m(llzll) for all z G CN .(5)

C (i) О (ii): By the Surjectivity criterion 26.1 of [9], p maps E (q) ( R ⁿ ) onto E N if and only if for each bounded set A in ( E (q) ( R ⁿ )) b the set (p ⁰ ) ^- 1 (A) is bounded in ( E N) )^ With the commutative diagram the first part of the theorem is proved.

• (ii)    ^ (iii): Fix any n G N and set Bn := {f G H(CN) : kf ||^_n,n,N 6 1}. Using (ii) with B = HN) П Bn, we deduce that there exist m G N and C > 0 such that

3.    Sufficient conditions

l|g|U,o,N 6 C for all g G HN ) П Bn.                         (6)

Let f G HN) be fixed. If ||f ||^n,n,N = 0 or ||f ||^n,n,N = ^, then (3) is trivially true. In case 0 < ||f ||^n,n,N < ^ we use (6) with g = kf ц f—^. Then we have kf U,0,N 6 C kf U,n,N .

This means that (3) holds.

Implications (iii) ⇒ (iv) ⇒ (ii) are easily checked. B

Throughout last three sections we suppose that Q = { ш _п } П—1 G Wnq . We start by

Proposition 3.1. Let Q = { ш _п } П—1 G W^q. Then the space E (q) ( R ⁿ ) is nonquasianalytic.

That is, there is a function f G E(q)(Rn)\{0} such that f (a)(0) = 0 for all a G nN .

C First we choose 0 = t o < t i < ... satisfying

∞

f Шп (t)

J   t2

t _n

Then we introduce a function

dt

< 4 n ³

for each n ∈ N .

^(t)

nω n

(t)

for t G [0,t ₁ ), for t G [t n ,t n₊1 ) .

Since we assume that wn(t) 6 ш _n+1 (t) for t >  0 , it follows that ш is nondecreasing on [0, to ) . Next, ш_n(t) = o(ш(t)) as t ^ to and

“           — tn +1

/dt = XX /

"I                   n—1 +

1                           t n

nШ n (t) t ²

“ 1

dt 6        <  ∞ .

n ²

n—1

By Lemma 3.2 of [2] we find a cotinuous nondecreasing function a : [0, to ) ^ [0, to ) such that ш(t) = o(a(t)),    t ^ to ; a(2t) 6 4a(t) for all t >  0;

∞

/ dt <  to .

J t2

Using Proposition 2.3 of [5] for the a and compact set K = { 0 } , we construct a function ^ G C “ (R N ) with the following properties:

^(x) = 1 for x G [ — e,e ] ⁿ ;  supp ^ C [ - 3s, 3 e ] ⁿ ;

A_V,_CT := j | b(t) | e ^{CT ( k t k )} dt< to .

R ^N

-

Here b(t) = J ^(x) e R ^N

^{i h t,x i} dx is a Fourier transformation of ϕ .

We wish now to show that ^ G E(q)(Rn ). By the Fourier inversion formula we have l^(a)(x)l 6

(21N /

R ^N

e¹^ dt 6

(2_n1)N / 1Ж1И1 ^{| а |} dt 6

(2Лр j l b(t) | е^шП-^№ dt • exp R ^N

RN sup (|a| log |t| - Wn(ktk)) 6 teRN\{o}

—1^ [ | b(t) | e^* dt • e ^ -n ^{( | a | ) (2n) N} J

.

R ^N

Since шn(t) = o(ш(t)) = o(o(a(t))) = o(a(t)) as t ^ ro, there is an Mn > 0 such that j j'b(t)l

R ^N

e ^ n (lltll) dt 6

j l b(t) j

R ^N

e CT^{( k t k )}+M n dt =

e ^{M n} A ϕ,σ .

Hence, eMn A

| ^ ^{( a )} (x) | 6 /„ x м e ^ ^n ^{( | a | )} for all a G N N .

(2n)N

This means that ^ G E (q) ( R ⁿ ) . Setting f (x) = ^(x) — 1 we finally obtain the result. B

To formulate the main result of the section we need some notation. For a nonquasianalytic function ш we define the function Р_ш : CN ^ R as follows:

∞

Р_ш (x + iy) = ¹ / ^k x ⁺ ty ^{k )} dt for x,y G R N .

nJ     t ² + 1

-∞

It should be noted that in earlier papers dealt with extension theorems (for instance, in [8] and [4]) the function Р_ш was considered for N = 1 only. As is well known, in case N = 1 , Р_ш is harmonic in the open upper and lower half plane and it is continuous and subharmonic in the whole plane C . Moreover, ш( | z | ) 6 Р_ш (z) for z G C .

Theorem 3.2. Let Q = { ш _п } П=1 G W^ q . Suppose that

• (I)    for each n G N there exist m G N and C >  0 such that

Рш п (z) 6 W m ( k z k ) + C for all z G C N .

Then the operator p : E (q) ( R ⁿ ) ^ E^) is surjective.

C Let us show that condition (iv) of Theorem 2.2 holds. Fix any n ∈ N . Assume that f G H (Q) satisfies (4). Then there are nf G N and Df > 0 such that

| f (z) | 6 D f e    f ^{( k} z ^{k )} for z G C N .

Given z = x + iy G C N with y = 0 , we define the entire function

F : C ^ C,

^{F (w):}= ^f(^z+w r y r)

for w ∈ C.

We can rewrite (7) as

| F(w) | 6 Df e^ nf ^{( k} x ^{k + | w | )} for all w G C .

Next, since

Im

(x^{+ w} k yr)

= | Im w | ,

• (4)    implies that

  | F(w) | 6 exp

  
  

  ^n | Im w | + ш_п

  
  

  (°x^+w r y r °))

  
  

  for w ∈ C .

  
  
  
  

By the Phragm e n-Lindel o f principle (Theorem 6.5.4 in [6]) we find that for u G R , v G R \{ 0 }

∞ log |F(u + iv)| 6 |v [   lOgJF(t)| 2 dt + |v|d,

n J (u — t) ² + v ²

-∞ where

π

d = limsup —- [ log If (ге^г6 )| r →∞ π r

sin 9 d9 .

Using (8) we have

π

π

— - [ log ^| F (re i ⁶ ) ^| sin 9 d9 6-- [ (log Df + wn_f ( k x k + r)) sin 9 d9 = πr                  πr           ^f

4 /logDf + Wnf (kxk + r) πr    r for all r > 0.

Nonquasianalyticity of ω _{n f} gives us that

∞∞

^n f ^{(r +} k x^k)       Г ^n f ^{(r +} k x^k)          f Un f (s)

—----—-— =  / —---о----ds 6  / —— ds ^ 0 as r ^ to r + kxk J         s2              J s2

r+ k x k                            r+ k x k

By the above this means that d 6 0 . Now, using (9) in (10) and (I), we have

∞ log |F(u + iv)| 6 ” У

-∞

^ ^{n ( k} x ⁺ t i\\ ID ₌ ( u — t ) ² + v ^{2 dt}

∞

= и

-∞

^ ^{( x + (u + vt)} \ У \ ||) t ² + 1

∞ dt=1 /

-∞

^ n ( k (x + u ^ ) + tv Д k )

t ² + 1

dt =

yy x + u ы>+ iv ы)

6 ω_m

yy

(° (x ⁺ u ы>⁺ iv w

^ + c .

Setting u = 0, v = kyk we get log |f (x + iy)| =log |F(i|yk)| 6 ^m(|x + iyk) + C.

Thus,

| f (z) | 6 e ^C e ^ ^{m ( k} z ^{k )} for all z g CN with Im z = 0.

By continuity this inequality holds for all z ∈ C ^N . Theorem 3.2 is thus completely proved. B

Corollary 3.3. Suppose that Q = { ^ n }^ ! G Wnq satisfies

(II 1 ) for each n G N there exist m G N and C >  0 such that w _n (2t) 6 w_m (t) + C for all t >  0 ;

(II)

(II 2 ) for each n G N there exist m G N and C >  0 such that

∞

4 Г Wn(yt)

dt 6 w_m(y) + C for all y >  0.

nJ t² + 1

Then E (q) ( R ⁿ ) admits a version of Borel’s extension theorem for all N ∈ N .

C Fix any n E N and find m i >  n and D i > 0 such that

∞

4 Г w n ^{( y}t) dt 6 ^ m i (y) + D i for y >  0 .                       (11)

n J t² + 1

Next, for the m i there exist m E N and D 2 > 0 such that

Wm 1 (2t) 6 W m (t) + D 2 for t >  0 .

Combining (11) and (12), we have for all z = x + iy E C ^N

∞

P^ n ^(z) =

1 [ W n ( k x + ty k ) nJ     t ² + 1

-∞

2 7 w n ( k x k + t H y H )

^{dt 6} nJ t ² + 1 dt ⁶

, 1 /и l ± l ,1^2 7 w„((kxk + 1М)«)Л^

⁶ 2^wn(kx ^{k +} hlD ⁺ n -----t^+i---- ^{dt 6}

6 ' Wn( k x | + Ы) + ⁴Wm , ( | x k + k y | )+ D i 6

^{6 w} m , ⁽ k ^x k ⁺ kyk) ⁺ D i 6 ω _{m 1} (²max ^{k x ^k , k y k^{} )} + D i 6

6 Wm(max{kxk, kyk}) + Di + D2 6 Wm(|z|) + C, where C := Di + D2. This means that condition (I) of Theorem 3.2 holds. So p maps E(q)(Rn) onto E(NΩ) . B

Remark. Let us explain how results of [8] and [4] for spaces of ultradifferentiable functions (UDF) of minimal and normal type can be derived from the present results. First recall that condition

• (I ⁰ )    for each n E N there exist m E N and C >  0 such that

РШп(z) 6 Wm(|z|) + C for all z E C provides that Borel’s extension theorem holds for the corresponding class E(q)(Rn) of minimal or normal type independently of the number N of variables.

In case of spaces of minimal type (see [8]), (II i ) means that w(2t) = O(w(t)) , t ^ ro . That was the general assumption of [8]. It is not hard to see that (II 2 ) ⇔ (I ⁰ ) in this situation. Indeed, in the proof of Corollary 3.3 we just have proved that under assumption (II 1 ), (II 2 ) implies (I), and so (I ⁰ ). Implication (I ⁰ ) ⇒ (II 2 ) follows from

∞∞

• ⁴ [ y dt 6 ⁴ [ ;   ' dt = ../„(iy) 6 2    . + 2C =

4.    Necessary conditions

nJ t² + 1 nJ t² + 1

= 2mw(y) + 2C = W 2m (y) + 2C for y >  0 .

In case of spaces of normal type, in Lemmas 2.5 and 2.7 of [4] it was shown that (II 1 ) ⇒ (II 2 ) and (II 1 ) ⇔ (I ⁰ ). So (II) ⇔ (II 1 ) ⇔ (I ⁰ ).

Assume that Q = { w _n } 7 ==i E W^q satisfies the additional condition (A) for each n E N there are m E N and A_n > 0 so that

Wn(x + y) 6 Wm(x) + Wm(y) + An for X, y >  0 .

Note that analogous assumption was also made in [4] for spaces of normal type (see Definition 6.1 of [4]). In case of spaces of minimal type, (13) is a simple consequence of the general assumption w(2t) = O(w(t)) , t ^ ro .

We start by several lemmas.

Lemma 4.1. Suppose that Q = { ш _п } П=1 E Wnq has property (A) . For each n E N there exists an m E N such that for every e >  0 we can find a C > 0 with

Рш_п (z) 6 e | Im z | + Wm ( | Re z | ) + C for z E C.

C Fix any n E N and find m E N and A n > 0 so that (13) holds. Next, for an arbitrary e > 0 choose r >  0 with

∞

² [ "  ' dt

nJ t ² + 1

r

We have for x >  0 and y >  0

P^ n ^{(x +} iy) =

∞ y [ ШпИ

π       t ²

-∞

x +1 | ) + y ²

∞

dt6 y 7

^W m ^{(x) + W} m ^{(t) +} An

t ² + y ²

dt = W m (x) + I m (y) + A n ,

where I m (y) : =

∞

— / ^mMy dt. If y 6 1 , then

П J t ² + y ²

I _m ( y ) =

∞

2 Г wm^yt) dt 6

n J t ² + 1

π

∞

Г ^W m ^(t) , t₂ + 1 dt =: Dm <  ro .

If y >  1 , then

I _m ( y ) =

r

Wm(t) ^ , 2y t ² + y ² dt ⁺ n

∞

[ Wmt^ dt 6 t ² + y ²

r

π

r/y               ∞

{ W m iyT dt +- /wm² dt 6 w m (r)+ ey.

J t² + 1       П J t² + 1

0 r

Hence,

Im(y) 6 ey + Wm(r) + Dm for all y> 0, and so,

P^n(x + iy) 6 Wm(x) + ey + C for x > 0, y > 0, where C Since

:= w _m (r) + Dm + A n . By continuity the preceding inequality holds also for y = 0 .

P^n(x + iy) = P^n(x - iy) = P^n(-x + iy), we finally obtain the result. B

Lemma 4.2. If Q = { w _n } n=1 E Wnq has property (A) , then for each n E N we can find an R_n >  0 such that for every R >  R_n there exists an r >  0 for which

r

2R f W n+i (t) P^ n ^{(iR) 6} n J t ² + r2 dt.

<1 Use of (1) gives that p        2RZ in+i(t) . ,  p^_2Rr in+i(t),.,r

^Р Ш п ^(iR) 6 — t ₂ + r ₂ dt - ^{log R +} Cn = ~ t ₂ + r ₂ dt ⁺ Lr,R,      ⁽¹⁶⁾

0                                           0

where

∞

L rR                dt -    R + Cn .

r

Put Rn := e^{Cn +1} . Given R > Rn choose r >  0 such that

∞

^2R [ dt< 1.

n J t² + R ²

r

Then L_r,R <  1 — log Rn + Cn = 0 . Use of this in (16) gives (15). B

In the next lemma we construct a special family of polynomials. Let us first introduce two new functions. For k E N and r > 0 we put ik (t) : =

ik (t)

r(ik ) - (r)log t + ik (r)

for t E [0, r]

for t E (r, to )

and

P ^ ^r (x + iy) := <

∞ | _π y |

-∞

ir ( | t | )

(t — x) ² + y ²

dt

for y = 0

(x + iy E C)

^r ^{( | x | )}

for y = 0

Pω _kr has the same properties that Pω , i. e. Pω _kr is harmonic in the open upper and lower half plane and it is continuous and subharmonic in the whole plane.

Lemma 4.3. Suppose that Q = { i _n } n=i E W” q satisfies (A) . There exists a family of polynomials {gR,_n(Z ) : n E N, R E [R _n , to ) } of one variable Z E C with the following properties:

1) for each n E N and each R > Rn gR,n(iR) > expP(iR);(17)

2) for each n E N there exist m E N and C > 0 such that lgR,n(Z)| 6 Cexp (m| Im Z| + im(|Z|)) for all R E [Rn, to) and Z E C .(18)

< Given n E N we find an Rn > 0 according to Lemma 4.2. Next we fix any R > Rn and find r > 0 such that (15) holds. Then

2R r i n₊i (t)      2R r i n+i (t ),₊ ,_p

РШп (iR) 6 ^ J t2 + r2 dt = n J t2 + r2 dt 6 P^n+i (iR) •

Applying Lemma 1 of [1] to the subharmonic function P^n+1 (z) and the point ^ = iR, we construct an entire function gR,n(Z), Z E C, for which gR,n(iR) = exp РшП+1 (iR),(20)

| g R,n (Z) | 6 A(1 + | Z | ² ) ² exp P i n ₊₁ (Z) for all Z E C                  (21)

Here A is an absolute constant and P ^ r ₁ (Z) := sup |р _ш г₊₁ (Z + w) : | w | 6 1}• Combining (20) and (19), we immediately derive (17).

In order to show that (18) holds, we estimate F^r (Z) . Since wn +i (t) 6 Wn +i (t) it follows that P ^ r₊₁ ^(Z) ^{6 P} W n +1 ^(Z) , and so, P^ r _{+ 1} ^(Z) 6 ^P1 +1 ^(Z ) ^{for al}l ^{Z E} C

Next, by Lemma 4.1, there are k E N and D i > 0 such that

Рш _n+1 (z) 6 k | Im z | + Wk ( | z | ) + D i for z E C .

In [3] it was proved (see inequality (5) of [3]) that

Wk(t + 1) 6 Wk(t) + Bke2 for all t > 0, where Bk is determined by (2). Thus,

Pl Ж) 6 Pl₊ Ж) 6 k | Im Z | + Wk ( | Z | + 1) + k + D i 6 k | Im Z | + W k ( | Z | )+ D, n+1          ^{n +1}

where D := B k e ² + k + D i .

It is easily checked that

(1 + | Z | ² ) ² 6 e ^{4log( | Z | +i)} for Z E C.

Now we can continue (21) as follows

| g R,n ^(Z) | ⁶ A^exP (^{k | Im Z} | ⁺41og^{( | Z} | ⁺ 1) ^{+ W} k ^{( | Z} | ) ⁺ D) .

Setting m = k + 4 and C = Aexp(C k + Ck +i + Ck +2 + Ck +з + D) , we finally obtain (18).

Proof of the fact that gR,n are polynomials is the same as in Lemma 2 of [1], so we omit it. Our result is thus completely proved. B

The main result of the section is

Theorem 4.4. Let Q = { w _n } ^=i be a weight sequence in W nq with property (A) . If

E (q) ( R ⁿ ) admits a version of Borel’s extension theorem for at least one N ∈ N , then

• (III)    for each n E N there exist m E N and C >  0 so that

Рш„ (iy) 6 W m (y) + C for all y >  0 .                         (22)

C First note that if p : E (Q) (R N ) ^ E ( N ) is surjective for some N >  2 , then it is also surjective for N = 1 .

Assume that there is an n 0 ∈ N such that for each m ∈ N and each k ∈ N there exists an R_m,k > R_{n 0} such that

Рш n₀ (iR m,k ) >W m (R m,k ) + k.

Here R n ₀ is determined by Lemma 4.2.

Let {gR,_n(Z ) : n E N, R E [R _n , to ) } be a family of polynomials with properties of Lemma 4.3. Then there are n i E N and D i > 0 such that

| g r,n o (Z) | 6 D i exp (n i | Im Z | + w^ ( | Z | )) for all Z E C .

Setting f_m,k := D- gR m k ,n ₀ , we can rewrite the previous inequality as | f m,k (Z) | 6 exp (n i | Im Z | + W n 1 ( | Z | )) for all Z E C .

Next, from (17) with n = ng and (23) we have for all m,k E N fm,k (iRm,k ) =    gRmk ,no (iRmk ) >    exp Рш (iRm,k ) >    exp Wm(Rm,k) .     (25)

D i    ’               D i         0            D i

Being polynomials f_m,k are in H ^q) - From (24) and (25) it then follows that assertion (iv) of Theorem 2.2 is false. Thus, the operator p : E (q) ( R ) ^ E^ is not surjective. This contradiction proves the theorem. B

Remark. It should be noted that Theorem 4.4 gives us the corresponding necessary conditions of [8] and [4] for spaces of UDF of minimal and normal type. Moreover, in these two cases condition (II) of Corollary 3.3 is equivalent to condition (III) of the previuos theorem (see [4, 8]). This means that whole criteria of [8] and [4] can be derived from our present results.

5.    Examples

One of the classical nonquasianalytic weight functions is ^(t) = t ^a , 0 <  a < 1 . It was shown in [8] that space of UDF of minimal type defined by this function admits the analog of Borel’s extension theorem. In contrast, the corresponding space of normal type does not admit this analog (see [4]). Let us consider

Example 5.1. w _n (t) = t ^a n , 0 < an t a 6 1 .

We should like to verify condition (II) of Corollary 3.3. It is easily seen that (II i ) holds. Next, for n E N and y >  0 we have

∞

4 Г ^n^yt)   = an n J t2 + 1 dt y

i

∞

4 / d 6 У nJ t2 + 1

i

∞

J Mdt =^{y a n} i

n(1 - a n ) ’

Obviuosly, we can find a C > 0 such that yan —(1------) 6 yan+1 + C for all y > 0.

This means that (II ₂ ) also holds. Thus the space E (_Q) (R ^N ) with Q = { t ^a n } n=1 admits a version of Borel’s theorem for all N ∈ N .

It is of particular interest that an could tend to 1, whereas w(t) = t is not a nonquasi- analytic weight function.

t loge (e+t)

Another well-known weight function is ^(t)

, where в > 1 . Recall (see [8] and

[4]) that Borel’s theorem does not hold for the corresponding spaces of UDF, both of minimal and normal type. Now we wish to consider a sequence of such functions.

Example 5.2. v n (t) = _log en _(e+t) , вп l в >  1 .

Without loss of generality we can assume that в 1 < в + 1 . First note that Q = { w _n } n=₁ satisfies condition (II i ), and so, condition (A) . Now, let us show that condition (III) of Theorem 4.4 does not hold. For y >  0 we have

∞ y J d(log(t2 + 1)) n 0 logen (e + yt)

∞

β _n

= y — π

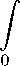
log(t ² + 1) dt log ^e n ⁺¹ (e + yt) e + yt

²     ^n ⁽ yt)

^{P (}i^y) = nJ t2 + 1 ^dt =

Put

t _y

y + Уу² +4(e - 1)

Then t ² + 1 >  e + yt for t > ty . Hence, for an arbitrary m E N we can write

P^ n (iy) > y ²

∞ вп [      1 dt

П J log ^e n (e + yt) e + yt t y

βn          y

^п(в п - 1) log ^e n ^{- 1} (e + yty )

вп      log ^e m (e+ y)

п(вп — 1) logen-1(e + yty) ‘ logem (e + y) logen-1(e + yty)

Since em > в > вп — 1, the quotient tends to ∞ as y → ∞, and so, (III)

does not hold. By theorem 4.4 we derive that p : E (q) ( R ⁿ ) ^ E (N) is not surjective.