On classical and quantum mechanical problem of two material points in three-dimensional Lobachevsky space

By analogy with the constructions and conclusions of works [1, 2] and relying on the definition of the center of mass given in works [3], we postulate its immobility in spaces of constant curvature, in this case in the three-dimensional Lobachevsky space, and consider the problem of two particles with an internal interaction described by potential, depending on the separation between particles. The essence of the statement, which replaces the formulation of the theorem on the center of mass in the three-dimensional Euclidean space, is that in spaces of constant curvature: Lobachevsky, on the 3-sphere and in three-dimensional elliptical space, there is a frame of reference in which the center of mass of the system of particles is at rest.

1.    Variables of the center of mass and relative coordinates for a system of two particles

Since the formalism used below, despite the fact that it allows one to unify the description of the geometries of a num-

О классической и квантово-механической задаче двух материальных точек в трехмерном пространстве Лобачевского

Ю.А. Курочкин, Н.Д. Шайковская, Д.В. Шёлковый

Институт физики имени Б.И. Степанова Национальной академии наук Беларуси, г. Минск, Беларусь

Классическая и квантовая задачи о движении двух частиц в трехмерном пространстве Лобачевского сформулированы относительно центра масс с произвольным положением. Выписаны уравнения Гамильтона-Якоби и Шрёдингера задачи и найдены их решения. Показано, что приведенная масса системы зависит от относительного расстояния. Сформулированы и решены классическая и квантовая задачи жесткого ротатора в трехмерной сфере и пространстве Лобачевского. Исследованы зависимости периодов колебаний ротатора от отношения масс образующих его частиц при фиксированной полной массе в случаях пространств постоянной кривизны.

The following definition of the center of mass coordinates of two particles with masses m ₁ and m ₂ is used

X i           m 1 X ⁽¹⁾ + m ₂ X ⁽²⁾

C = ^г y mX aT+ m ^ x WJ mX aT+ m ^ X W) ’

Here the corresponding biquaternions are given over the complex numbers, and not over the double ones, as it was in the case with the 3-sphere [1,2].

The three-dimensional independent coordinates of the center of mass will be the components of the vector

( g ⁽²⁾ , — _(;    ) _

q ⁽²⁾ — q ⁽¹⁾ — [ q ⁽²⁾ , q ⁽¹⁾ ] 1+^W² ) )

. X C _ . m 1 X ⁽¹⁾ + m ₁ X ⁽²⁾ X 0 C      m 1 X 0 ¹ ) + m ₂ X 0 ²⁾

The coordinates of two material points in the embedding fourdimensional space will be the components of the biquaternions:

X ⁽¹⁾ _ ‘X 0 ¹ ) + X ⁽¹⁾ , X ⁽²⁾ _ ‘X 0 ²⁾ + X ⁽²⁾ , (3) where г ² _ — 1 . The ends of the vectors (biquaternions) lie on the upper field of the pseudo-Euclidean space hyperboloid, on which the real Lobachevsky space is realized. For convenience, the radius of space curvature is assumed to be unity. Then

X ⁽¹⁾ X ⁽¹⁾ _ — 1 , X ⁽²⁾ X ⁽²⁾ _ — 1 . (4)

Let us also introduce four-dimensional Y 1 and Y > and threedimensional я У ¹^, д У ¹^ coordinates of points relative to the center of mass, determined similarly to (8) and (9), namely

X(1) _ Y1XC,      X(2) _ Y2XC,(11)

moreover

Y1 = —X(1) JXC,       Y2 = —X(2) XX C.(12)

It is clear that

Y12 _ Y2 Y1.(13)

As independent coordinates, it is convenient to use the Beltrami coordinates, which are components of vectors on the sphere [5]

(1)(2)

a (1) = -г-X—   a(2> = q ‘ v(1) , q ‘ v(2)

X0

with the law of addition (subtraction)

q”_ ( q •± q >_ qTOT coinciding with the composition law of F.I. Fedorov [6]. Here, parentheses denote the usual scalar, square brackets denote the vector product of vectors. In variables (5), expression (2) has the form

_ m 1 q ⁽¹⁾ / У1 + ( g ⁽¹⁾ ) ² + m 2 q ⁽²⁾ / V1 + ( q ⁽²⁾ ) ² q C =     m 1 /, ' + q + m 2 / ^1 + ( g ⁽²⁾ ) ²     '

As noted earlier, expression (7) for the coordinates of the center of mass coincides in form with a similar expression for the coordinates of the center of mass in a three-dimensional flat space, in which the expressions for constant masses m 1 and m ₂ are replaced by mass expressions with the dependen ce of masse s on coordinates m ₁ /V 1 + ( g ⁽¹⁾ ) ² and m 2 / У1 + ( g ⁽²⁾ ) ² .

We also note that this definition coincides with the definition given in [6], if we take into account that g ² _ — th ² r , where r is the distance between two points. As it follows from the formula (7) (and shown in [7]), such a definition can be generalized to an arbitrary number of particles. The biquaternion analogue of the relative variable for two given particles is the operator

Y 12 _ —X ⁽²⁾ X ⁽¹⁾ ,               (8)

defined as

X ⁽²⁾ _ Y 12 X ⁽¹⁾ .                 (9)

Then for the first particle

(1) _{_}

_X (1)

‘X p ⁼

- q y       _-i X _C

\ 1 + m 2 yrr^ ² ’ ^X 0 C

^{_ (} q y^i}, g C ),

and for the second one we get:

(2) _{_}

X ⁽²⁾

‘ X ^_

^{q y}        -i ^{X C}

\ 1 + m i yrr^ y , X 0 C

^{_ (} я У²⁾, я C ).

where g ⁽¹⁾ and g ⁽²⁾ are defined from Y ₁ and Y ₂ respectively. It is easy to verify the validity of formulas (14) and (15) by direct calculation. It should be noted that g ⁽¹⁾ and g ⁽²⁾ are expressed in terms of relative variables q _y and center of mass variables q _C .

From (13) it follows that

g y _ ( g ⁽²⁾ , — g ⁽¹⁾ ) _ ( я У²⁾, — я У^1} V         (16)

Independent three-dimensional coordinates of relative motion, defined as components of the relative motion vector

The variables introduced satisfy the relations

^X C ^X C ^{_ — 1} ,  ^Y 12 Y ^Z12 ^{_ 1} ,

_ ^Y 12 ^{— Y} I2 q y ^_ Y . + Y .

/    X (=>     X (1> \

\ "X 0 ²⁾ ’*X 0 ¹)/

Y 1 Y 1 _ 1 ,   Y , Y 2 _ 1 .              (17)

2. Two material points on S31. Non-relativistic classical problem

and the transverse reduced mass

The action for the problem of two material points in threedimensional space, interacting with forces that depend only on the relative variable, we write in the form [1-3]

W =

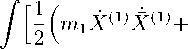
+ m 2 X ⁽²⁾ X ⁽²⁾) - V ( Y ц) dt. (18)

m ₁ m ₂ ( m ₁ + m ₂ )

^{M ±} = m 1 + m 2 + 2 m 1 m 2 ch r^.

The Hamiltonian of the system is therefore equal to

H =2 [ м ь ⁽ r ) r " ^{2 +}

+ p v ( r ) sh ² r ( 9² + sin ² 9²)] + U(r₁₂).

Here it is immediately taken into account that the operation of differentiation and conjugation are commuting. The dot above the letters denotes differentiation with respect to time. Expression (18) will take a standard form if we pass to independent variables q ⁽¹⁾ and q ⁽²⁾ . In this case

W = j [ 2 ( m 1 gab ( q ⁽¹⁾ ) qa^ q ⁽¹⁾ +

+ m 2 g ab ( q ⁽²⁾ ) q a ² q ⁽²⁾ ) - Ф ( q y )] dt,       (19)

where gab =          - ^aq^l        (20)

1 + q ² I 1 + q ² I

It is easy to check that the expression for the Hamilton function (25) in the flat limit r —> 0 transforms into the Hamiltonian function of the plane problem for a reduced mass particle. The corresponding coefficients transform into the expression for the reduced mass

m 1 m 2

м = —г— . m ₁ + m ₂

Thus, in spaces with curvature, reduced particle masses can be interpreted as dependent on coordinates, as it also seen from (7) (see also [8]). The same is true for composite systems: the reduced masses are functions of the coordinates.

Taking into account the form of the Hamilton function (25) and the following definitions of generalized momenta

is the metric tensor of the three-dimensional Lobachevsky space in variables that are components of vectors on the sphere. In expression (19), according to the accepted assumption, we set q C = 0 and write it in spherical coordinates. Then

∂L

Pr = YT, ∂r

p * = ⁸L  p * = ^dL-

∂θ        ∂ϕ

W =

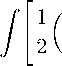
m ₁ r 2 + m ₁ sh ² r ₁ ( 9 2 +

sin ² 9ф 1 ) +

+ m 2 r 2 + m 2 sh ² r 2 ( 9 2 + sin ² 9ф 2 )) - U ( r ц)] dt. (21)

Replacing in (21) the coordinates of individual particles with relative variables r, θ, ϕ in accordance with formulas (14), (15) with q C = 0 , we get the following expression for the action

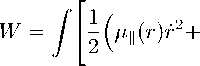
+ M i ( r )sh ² r ( 9 ² + sin ² 9ф ² )) — U ( r ₁₂)j dt,   (22)

where we have introduced the longitudinal reduced mass of two material points

µ ∥

= m ₁

I

m 2 + m ₁ m ₂ ch r m 1 + m 2 + 2 m ₁ m ₂ ch r

)

+

+ m 2

I

m 1 + m ₁ m ₂ ch r m 1 + m 2 + 2 m ₁ m ₂ ch r

)

we consider the Hamilton-Jacobi equation

1    ⁽ dW ) ²        1

² M h ^{( r} ) \ ^dr ) ^{+ 2} M i ( r ) sh ² r^X

X

7 dw\     1 / dw\ "

"d9 "J ⁺ sin ² 9 \"дф J

9W

+ U ( r ) + "dT = 0 .

The last equation allows separation of variables

W = -Et + W r ( r ) + W _e ( 9 ) + W * ( ф ) , and decomposes into the following equations

∂W ∂ϕ

= M * ,

/ dW \²

("99 ) ⁺

⁽ dW ^{) 2} M h ( r ) M ² V dr/ p i ( r ) sh ² r

M²- = M ² , sin ² 9

= ² M h ( ^{r )(} E ^{- U} ( ^r )) .

These equations are easily integrated. Wherein

W * = М * ф,

W r

W e =

-

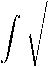
M ²

M2

^ϕ dθ, sin ² 9

-

M h M ²

M l sh ² r

Substituting the last expressions into (29) and differentiating with respect to constants, we obtain equations for the particle trajectory

∂W

= ^ф 1 ^{- ф} 2

∂M ϕ

-

-

r 2

r 1

-

θ 2

θ 1

M ϕ sin ² 9\[м2

dW _ Г^{e 2}

EM = Je i ^

M l ^{( r} )

-

— de = о , ^M ϕ ²

sin ² θ

Mdθ

-

where the Hamiltonian is

H = - 2a lb + U ( r ) •          (45)

It is clear that the equation we have allows the separation of variables

* = R ( r ) Y m ( е,ф ) ,             (46)

where Y l^m ( е,ф ) are the spherical functions satisfying the equation

A еф У т ( е,ф ) =

M ²

-

M ² ϕ sin ² θ

Mdr

^{M (} r ) sh ² r 2 m _I [ E - U ( r )]

-

^µ ∥ M ² µ ⊥ sh ² r

. (37)

The law of motion is given by the expression

∂W dE = t2

-

t 1

-

A еф УГ ( е,ф ) = -l ( l + 1) Y ^m ( е,ф )      (47)

for l = 0 , 1 , 2 , • • • and the radial part of the wave function is the solution for the equation

d2R dr2 +

µ ∥

d

M ± sh ² r dr

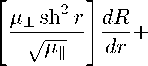
+ (2 m i ( E - U ) - ^{M l} l ⁽ l ⁺ 2 1) R = 0 • у               M ± sh r у

-

r 2

V • ¹ ф

M l ^{( r} ) ^dr ____________ '² M l [ E - U ( r )] - h

.

4. A particular problem of a rigid rotator in spaces with constant curvature

3. Schrödinger equation for two material points in Lobachevsky space

The general formula for the classical kinetic energy of any system is

T ci = 2 ^ g ij ^{( q} ) ^q i ^q j ,

where q i - generalized speeds, g ij ( q ) - generalized masses. The corresponding operator in quantum mechanics is

T _q = -^ A BL ,

where A _BL - the Laplace-Beltrami operator, which can be obtained from the general expression

As we know, in the case of a constant relative distance between two points, a mechanical system is obtained, which is called a rigid rotator. Despite the apparent simplicity, this model for a flat space, both classical and quantum mechanical [9], find interesting applications, including in the theory of molecules and nuclear physics. From the approach developed above, as well as in accordance with works [1-3, 9], it follows that in spaces of constant curvature, a rigid rotator has features associated with the dependence of the reduced mass on the distance between points. These features are explored below. By formulas (21), (25) and the corresponding formulas in [2,3], the Lagrange function of a rigid rotator in three spaces: in the Lobachevsky space, on the 3-sphere and in the Euclidean space has the form

A BL = Ф ^d [ vgg 'j Л1 • g ∂q ⁱ         ∂q ^j

Since in our case the kinetic energy expression can be from (22), the Laplace-Beltrami operator has the form

L = A e^ + sin ² еф) ²) ,           (49)

△ BL =

∂

M ± >/M\i sh 2 r^dr

I" g ^ sh ² r d "I

^√µ ∥   ∂r

⁺ mST ^A ** '

seen

where

л 1 д / _ „ д \ , ^еф sin ede(   ^ede y ⁺

i д 2 sin ² e дф ² •

where the quantity A has the following expressions in the three spaces under consideration, respectively

A lob    R^ ^M ^lob ^sh ,

2 R

A sph   ^ R ^M ^sph ^sin R ,

A flat = ^ ^ flat r 0 ,

where

M \ lob —

m 1 m ₂ ( m 1 + m ₂ )

m 1 + m 2 + 2 m 1 m ₂ ch( r 0 /R ) ’

Accordingly, the Schrödinger equation becomes

∂ψ

i* = H*'

^M ^sph

m 1 m ₂ ( m 1 + m ₂ )

m 1 + m 2 + 2 m 1 m ₂ cos( r 0 /R ) ’

m 1 m 2

Mflat                 • m1 + m2

Solutions for the corresponding Hamilton-Jacobi equation in the case of a rigid rotator have the form

cos 4 AE

M ²

EAt   ,

ϕ = arctg    ⁴ _M ^AE tg    ^E_At   .

the Lobachevsky space, minimum for the 3-sphere. The corresponding curve for flat space lies between the two mentioned curves, with each of them tending to the flat space curve at R -→ ∞ . All three curves are similar.

In the quantum case, the Hamiltonian operator of such a system has the form

H = ₂ ^ℏ _I ² ∆ θ,ϕ ,

It follow s f rom the last formulas that the period of oscillations T ∼ A . Let us analyze how the period of oscillations depends on the ratio of the masses of particles (with a constant total mass). Denote the mass ratio β = m ₁ /m ₂ . Then

mR ²   2 r 0          β

⁼ 2 ^sh    R β ² + 1 + 2 β ch( r 0 /R ) ^{, (56)}

where the moment of inertia of the system is

I lob = 2 mR ² sh ^{2 r 0} ,  I flat = ^{mr 0} ,

2 R          2

I sph = 2 mR ² sin ^{2 r 0} .            (63)

mR ²   ₂

A _sph = ₂ sin

r 0

β

R β ² + 1 + 2 β cos

mr ₀ ²    β

^{A ♭ =} 2 (1 + β ) ^{2 .}

( r 0 /R )    ^,

If we fix the values of the constants E = 1 , M = 1 then from the condition 1 - ₄ ^M _AE ² >  0 it follows that A >  1 / 4 and therefore, for the solutions to make sense, the mass ratio cannot be arbitrary. Let’s take the values R = 2 . 5 , r ₀ = 2 , m = 1 . Then the condition A >  1 / 4 for three spaces leads to the following restrictions on the mass ratio of the particles of a rigid rotator

Alob > 1/4 :   0.142 < β < 7.04;

Asph > 1/4 :   0.207 < β < 4.83;

Aflat > 1/4 :   0.172 < β < 5.83;

We construct graphs of dependence of periods of oscillations on the ratio of masses in the range 0 . 21 < β <  4 . 8 . Figure 1 shows that the period of rotation of a rigid rotator, and hence the magnitude of the angular momentum, depends on the radius of space curvature R .

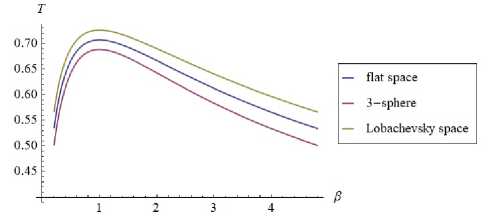
Figure 1. Graphs of rotation period on the ratio of the masses of the constituent particles at a fixed total mass of the rotator. Top graph – Lobachevsky space, average – flat space, bottom – 3-sphere.

Рисунок 1. Графики периода вращения в зависимости от отношения масс составляющих частиц при фиксированной общей массе ротатора. Верхний график – пространство Лобачевского, средний – плоское пространство, нижний – трехмерная сфера.

For the equal distances between the material points of the rotator and equal radius of the curvature for the Lobachevsky and 3-sphere spaces, the rotation periods are maximum for

The Schrödinger equation Hψ = Eψ gives the energy levels of the rigid rotator

ℏ ²

E l = _{2 I} l ( l + 1) ,

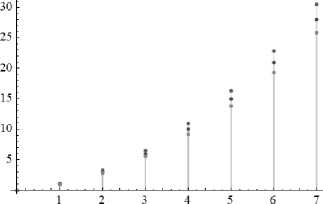
and the eigenfunctions of the Hamilton operator are equal to the spherical functions for all three spaces ψ = Y _l ^m ( θ, ϕ ) . The levels are degenerate, since each value of the orbital quantum number corresponds to 2 l + 1 magnetic number values. Figure 2 shows energy levels for quantum rotator in the spaces under consideration (we set here R = 2 . 5 , r 0 = 2 , m = 1 ).

Energy

— flat space

— 3—sphere

— Lobachevsky space

Figure 2. Energy levels for rigid rotator in spaces of constant curvature. Top point – 3-sphere, average – flat space, bottom – Lobachevsky space.

Рисунок 2. Уровни энергии для жесткого ротатора в пространствах постоянной кривизны. Верхняя точка – трехмерная сфера, средняя – плоское пространство, нижняя – пространство Лобачевского.

Conclusion

The paper solves the classical and quantum problems of motion of two particles in three-dimensional Lobachevsky space, relative to the center of mass. The Hamilton-Jacobi equation of the problem is formulated and its solutions are found. The corresponding Schrödinger equation allows the separation of radial and angular variables. It is shown that the reduced masses of the system depend on the relative distance between the particles. The classical and quantum problems ofa rigid rotator in three-dimensional Lobachevsky space are formulated and solved. The dependences of the rotator oscillation period on the ratio of the masses of the forming particles at a fixed distance between them and fixed total mass are obtained for three cases: Lobachevsky space, 3-sphere and three-dimensional Euclidean space.