On Line Tuning Premise and Consequence FIS Based on Lyaponuv Theory with Application to Continuum Robot

Published Online February 2014 in MECS

Sliding mode controller (SMC) is one of the influential nonlinear controllers in certain and uncertain systems which are used to present a methodical solution for two main important controllers’ challenges, which named: stability and robustness. Conversely, this controller is used in different applications; sliding mode controller has consequent disadvantages ; chattering phenomenon and nonlinear equivalent dynamic formulation; which chattering is caused to some difficulties such as saturation and heat for mechanical parts of robot manipulators or drivers and nonlinear equivalent dynamic formulation in uncertain systems is most important challenge in highly nonlinear uncertain system[1, 5-29]. In order to solve the chattering in the systems output, boundary layer method should be applied so beginning able to recommended model in the main motivation which in this method the basic idea is replace the discontinuous method by saturation (linear) method with small neighbourhood of the switching surface. To remove the above setbacks, control researchers have applied artificial intelligence method (e.g., fuzzy logic, neural network and genetic algorithm) in nonlinear robust controller (e.g., sliding mode controller, backstepping and feedback linearization) besides this technique is very useful in order to implement easily. Estimated uncertainty method is used in term of uncertainty estimator to compensation of the system uncertainties. It has been used to solve the chattering phenomenon and also nonlinear equivalent dynamic. If estimator has an acceptable performance to compensate the uncertainties, the chattering is reduced. Research on estimated uncertainty to reduce the chattering is significantly growing as their applications such as industrial automation and continuum robot manipulator. In recent years, artificial intelligence theory has been used in sliding mode control systems [31-40, 68]. Neural network, fuzzy logic and neuro-fuzzy are synergically combined with nonlinear classical controller and used in nonlinear, time variant and uncertainty plant (e.g., robot manipulator). Fuzzy logic controller (FLC) is one of the most important applications of fuzzy logic theory. This controller can be used to control nonlinear, uncertain and noisy systems. This method is free of some model-based techniques as in classical controllers [33-38]. The main reasons to use fuzzy logic technology are able to give approximate recommended solution for uncertain and complex systems to easy understanding and flexible. Fuzzy logic provides a method which is able to model a controller for nonlinear plant with a set of IF-THEN rules, or it can identify the control actions and describe them by using fuzzy rules. The applications of artificial intelligence, neural networks and fuzzy logic, on robot arm control have reported in [29-31]. In various dynamic parameters systems that need to be training on- line tuneable gain control methodology is used. On-line tuneable control methodology can be classified into two main groups, namely, traditional adaptive method and fuzzy adaptive method. Fuzzy adaptive method is used in systems which want to training parameters by expert knowledge. Traditional adaptive method is used in systems which some dynamic parameters are known. In this research in order to solve disturbance rejection and uncertainty dynamic parameter, on-line tuneable method is applied to artificial sliding mode controller.

Continuum robot manipulator is collection of links that connect to each other by joints, these joints can be revolute and prismatic that revolute joint has rotary motion around an axis and prismatic joint has linear motion around an axis. Each joint provides one or more degrees of freedom (DOF). From the mechanical point of view, continuum robot manipulator is divided into two main groups, which called; serial robot links and parallel robot links. In serial continuum robot manipulator, links and joints is serially connected between base and final frame (end-effector). Parallel continuum robot manipulators have many legs with some links and joints, where in these robot manipulators base frame has connected to the final frame. Most of continuum robots are serial links, which in serial robot manipulator the axis of the first three joints has a known as major axis, these axes show the position of endeffector, the axis number four to six are the minor axes that use to calculate the orientation of end-effector, at last the axis number seven to п use to avoid the bad situation. Kinematics is an important subject to find the relationship between rigid bodies (e.g., position and orientation) and end-effector in robot manipulator. The mentioned topic is very important to describe the three areas in continuum robot manipulator: practical application, dynamic part, and control purposed therefore kinematics play important role to design accurate controller for robot manipulators. Continuum robot manipulator kinematics is divided into two main groups: forward kinematics and inverse kinematics where forward kinematics is used to calculate the position and orientation of end-effector with given joint parameters (e.g., joint angles and joint displacement) and the activated position and orientation of endeffector calculate the joint variables in Inverse Kinematics[1]. Dynamic modeling of robot manipulators is used to describe the behavior of robot manipulator, design of model based controller, and for simulation. The dynamic modeling describes the relationship between joint motion, velocity, and accelerations to force/torque or current/voltage and also it can be used to describe the particular dynamic effects (e.g., inertia, coriolios, centrifugal, and the other parameters) to behavior of system[1]. The OCTARM continuum robot serially links robot manipulator has a nonlinear and uncertain dynamic parameters serial link 6 degrees of freedom (DOF) continuum robot manipulator.

Even though, sliding mode controller is used in wide range areas but, pure it has chattering problem and nonlinear dynamic part challenges. On the other hand, fuzzy logic controller has been used for nonlinear and uncertain systems controlling. Conversely pure fuzzy logic controller (FLC) works in many areas, it cannot guarantee the basic requirement of stability and acceptable performance. Although both SMC and FLC have been applied successfully in many applications but they have some limitations. The boundary layer method is used to reduce or eliminate the chattering and proposed fuzzy Lyapunov estimator method focuses on substitution fuzzy logic system instead of dynamic nonlinear equation to implement easily and avoid mathematical model base controller. To reduce the effect of uncertainty in proposed method, novel antecedent and consequent adaptive method is applied to fuzzy sliding mode controller in robot manipulator. The main goal is to design a novel fuzzy adaptive fuzzy estimation sliding mode methodology which applied to robot manipulator with easy to design and implement. Robot manipulator has nonlinear dynamic and uncertain parameters consequently; following objectives have been pursuit in the mentioned research: To develop a chattering in a position pure variable structure controller against uncertainties, to design and implement a Lyapunov fuzzy structure variable controller in order to solve the equivalent problems with minimum rule base and finally to develop a position fuzzy (antecedent and consequent) adaptive fuzzy estimation sliding mode controller in order to solve the disturbance rejection and reduce the computation load.

This paper is organized as follows:

In section 2, detail of dynamic equation of continuum robot arm, introduced the sliding mode controller and fuzzy logic theory are presented. Detail of tuning methodology which online adjusted both the premise and the consequence parts of the fuzzy rules is presented in section 3. In section 4, the simulation result is presented and finally in section 5, the conclusion is presented.

• II.    Theory

Dynamic Modeling of Continuum Robot: The Continuum section analytical model developed here consists of three modules stacked together in series. In general, the model will be a more precise replication of the behavior of a continuum arm with a greater of modules included in series. However, we will show that three modules effectively represent the dynamic behavior of the hardware, so more complex models are not motivated. Thus, the constant curvature bend exhibited by the section is incorporated inherently within the model. The model resulting from the application of Lagrange’s equations of motion obtained for this system can be represented in the form

F с о eff I = . (q) + + .(/) + + ^G (1)         ⁽¹⁾

where is a vector of input forces and q is a vector of generalized co-ordinates. The force coefficient matrix transforms the input forces to the generalized forces and torques in the system. The inertia matrix, is composed of four block matrices. The block matrices that correspond to pure linear accelerations and pure angular accelerations in the system (on the top left and on the bottom right) are symmetric. The matrix contains coefficients of the first order derivatives of the generalized co-ordinates. Since the system is nonlinear, many elements of contain first order derivatives of the generalized co-ordinates. The remaining terms in the dynamic equations resulting from gravitational potential energies and spring energies are collected in the matrix . The coefficient matrices of the dynamic equations are given below,

Feoeff =							(2)
	1	1	(   )	(   )	(   +   )	(   +   )
	0	0	1	1	(  )	(  )	⎥
	0	0	0	0	1	1
	1⁄2	-1⁄2	1⁄2	-1⁄2	1⁄2+     ( )	-1⁄2 +     ( )	⎥⎥
	0	0	1⁄2	-1⁄2	1⁄2	-1⁄2	⎥
	⎣0	0	0	0	1⁄2	-1⁄2     ⎦

. /=	⎡         + ⎢+	(   ) +       (  )	(   +   )	-         (  ) -         (  ) -        (   +   )	-         (  +   )	⎤	(3) ⎥⎥ ⎥
	⎢                     (    ) ⎢     +        (   ) ⎢	+	(   )	-         (  )	-         (  )	0	⎥⎥ ⎥
	(   +   )	(   )	m3	(   )	0	0	⎥⎥
	⎢ ⎢-     ( ) ⎢-     ( ) ⎢-        (   +   )	-         (  )	(   )	+  + + +    + +           (  )	+    + +         (  )		⎥ ⎥⎥
	⎢ -        (  +  ) ⎢	-         (  )	0	+     + +         (  )	+    +	/3	⎥ ⎥⎥ ⎥
	⎣	0	0	Is	Is	⎦

c .»'	⎡ ⎢⎢ ⎢      + ⎢ ⎢ ⎢⎢	-2       (  ) ̇ -2       (  ) ̇	-2     (  +  ) ( ̇  + ̇ )	- (   )( ̇ ) +(1⁄2)(  +   ) - (   )( ̇ ) - (   +   )( ̇ )	-       (  +  )	0⎤	(4) ⎥⎥ ⎥⎥
	⎢ ⎢ ⎢ 0 ⎢ ⎢ ⎢⎢	+	-2      (  ) ( ̇  + ̇ )	-      ( ̇ ) +(1⁄2) ( + ) -      ( ̇ ) - (   )( ̇ )	-2 (   )( ̇ ) - (   )( ̇ )	0	⎥ ⎥⎥
	⎢ ⎢ ⎢0 ⎢⎢	2        (  )( ̇ )	+	- (   )( ̇ ) -      ( ̇ )	-2      ( ̇ ) -      ( ̇ )	(1⁄2) ( + )	⎥ ⎥⎥
	⎢⎢ ⎢   (1⁄2) ⎢(    +    ) ⎢	2          (  )( ̇ ) -2      ( ̇ ) +2      ( ̇ )	2       ( ̇+  ̇) -2        (  ) ( ̇+ ̇)	2 (   )( ̇ ) +(1 ⁄4) ( + )	m3s3s2 (   )( ̇ )	0	⎥ ⎥⎥
	⎢ ⎢⎢          0	(1⁄2)(  +   )+ 2          (  )( ̇ )	2 ( ̇+ ̇)	m3s3s2 (   )( ̇ )	(1 ⁄4) ( + )	0	⎥⎥
	⎢ ⎣⎢        0	0	(1⁄2)(   -   )	0	0	(1 ⁄4) (    +    )⎦	⎥ ⎥

G.q/=

- тгд - m2g + fcn (Si+(1⁄2)61 - Soi)+k21 (Si - (1⁄2)6i - Soi)-m3g1

⎢⎡⎥

⎢^- m₂gcos ( 0i)+&12 (^S2+(1⁄2) ^2 - ^SO2)+^22(^S2-(1⁄2) ^2 - ^SO2)- m₃gcos ( 0i)⎥

⎢- m₃gcos (61 + e₂ )+ k₁₃ (s₃ + (1⁄2)0₃ - S₀3)+ k₂3 (S3 - (1⁄2)03 - S₀3)⎥ ⎢⎥

^⎢ m₂s₂gsin (0i)+ n^gsin (0i + ^2)+ m₃s₂gsiTi ( 0i)+^ii ($i + (1⁄2)0i - ■^01)(1⁄2) ⎥

⎢^{⎢                           +} к₂г (Si - (1⁄2)61 - Soi)(-1⁄2)                           ^⎥

⎢⎥ ⎢ m₃s₃gsm (01 + ^2)+^12 (^S2 +(1⁄2) ^2 - ^S02)(1⁄2)+^22 (^S2 - (1⁄2)^2 - ^S02)(-1⁄2)⎥

⎣           кгз (S₃+(1⁄2)03 - Sos)(1⁄2)+ k₂₃ (s₃-(1⁄2)03 - Sos)(-1⁄2)          ⎦

Sliding mode controller (SMC) : SMC is a powerful nonlinear controller which has been analyzed by many researchers especially in recent years. This theory was first proposed in the early 1950 by Emelyanov and several co-workers and has been extensively developed since then with the invention of high speed control devices [2]. The main reason to opt for this controller is its acceptable control performance in wide range and solves two most important challenging topics in control which names, stability and robustness [7,  17-20].

Sliding mode control theory for control of robot manipulator was first proposed in 1978 by Young to solve the set point problem ( ̇ 'd =  ) by discontinuous method in the following form [19, 3];

( <⁽ q , t ⁾   if S_t >0                   (6)

^{T (4,} ‘ )={ T_t ( q , t )    if S_t <0

where St is sliding surface (switching surface), i =  ,2,……,n for n -DOF robot manipulator, T, ( q , t )

is the I^th torque of joint. Sliding mode controller is divided into two main sub controllers: discontinues controller( ^dis ) and equivalent controller( ^eq ).

Robot manipulators are one of the highly nonlinear and uncertain systems which caused to needed to robust controller. This section provides introducing the formulation of sliding mode controller to robot manipulator based on [1, 6]Consider a nonlinear single input dynamic system of the form [6]:

X ( )₌ f ( ⃗⃗ ) + b ( ⃗⃗ ) и                             (7)

Where u is the vector of control input, X ^{( )} is the n^th derivation of X , X =[ X , ̇, ̈,…, X ⁽ n—1) _] T is the state vector, /( X ) is unknown or uncertainty, and b ( X ) is of known sign function. The control problem is truck to the desired state; X₄ =[ Хд , ̇ "d , ̈ "d ,…, Хд ⁽ n—1)_] T , and have an acceptable error which is given by:

̃= X - Хд =[̃,…, ̃⁽n-1) _] T                 (8)

A time-varying sliding surface s ( X , t ) is given by the following equation:

s ( X , t )=( +Я) n-l̃= 0

where λ is the positive constant. To further penalize tracking error integral part can be used in sliding surface part as follows:

s( X , t )=( +я) n-l

4∫ ̃ dt 5=⁰

The main target in this methodology is kept the sliding surface slope s( X , t ) near to the zero. Therefore, one of the common strategies is to find input U outside of s ( X , t ).

|^S²( X , t )≤-< | S ( X , t )|

where ζ is positive constant and in equation (11) forces tracking trajectories is towards sliding condition.

If S(0)>0 → s^s(t)≤-<

To eliminate the derivative term, it is used an integral term from t=0 to t= breach

∫ =0    dt^ ( t )≤-∫ :=0      →            (13)

S ₍ breach )- S ⁽0)≤-<⁽ breach ^-0)

Where breach. is the time that trajectories reach to the sliding surface so, suppose S( breach =0) defined as

S ⁽ 0 ⁾

о^-s⁽о)≤- q ⁽ breach )→ breach ≤

and

ifS (0)<0→0-5(0)≤- q ( breach )→

S (0)≤-<( breach )→ breach ≤ ^| - ⁽ “ )|

Equation (15) guarantees time to reach the sliding surface is smaller than |^(01 since the trajectories are outside of 5(t).

If breach — ⁵⁽⁰⁾ ^ error(x - X_d) — 0       ⁽¹⁶⁾

suppose S is defined as s (x, t) — (^ + A) x

— (x - x d. + A(x - xd.

The derivation of S, namely, 5 can be calculated as the following;

S — (x - x d ) + A(x - x d )                    ⁽¹⁸⁾

suppose the second order system is defined as;

X — f + и ^ S — f + U — Хд +            ⁽¹⁹⁾

A⁽x - x d ⁾

Where is the dynamic uncertain, and also since S — 0 and 5 — 0, to have the best approximation , U is defined as

U — -f + xd - A(x - Xd)

A simple solution to get the sliding condition when the dynamic parameters have uncertainty is the switching control law:

Udls — U - K(x, t) • sgn(s)

where the switching function ( ) is defined as fl      s > 0

sgn (s) —{-1s<0

(0s = 0

and the K(x, t) is the positive constant. Suppose by (21) the following equation can be written as,

^S2 (x, ^ — S • S — [f - f - Ksgn(s)] •

S = (f-f)^-K|5| and if the equation (22) instead of (23) the sliding surface can be calculated as

S(x,^ — (5; +A)2 (JoXdt/ = (x-xd)+

• 2 A (х-x d ⁾ -A²⁽x-x d ⁾

in this method the approximation of is computed as

U — -f + xd - 2A(x - xd) + A2(x - xd)

Therefore the switching function sgn(S) is added to the control law as

U — K(x, t) • Sgn(5)

Based on above discussion, the control law for a multi degrees of freedom robot manipulator is written as:

• T — TeQ + ddis

Where, the model-based component teq is the nominal dynamics of systems and    can be calculate as follows:

Teq — [o - Hf + C+G ) + 5]£>(28)

and Т д _is is computed as;

• —   •     ( )

The control output can be written as;

By (29) and (30) the sliding mode control of robot manipulator is calculated as;

T — [o-1 (f + C + G) + 5]o + K • Sgn(5)

The Lyapunov formulation can be written as follows,

The derivation of can be determined as,

У — IS^D.S + S7, OS

The dynamic equation of robot manipulator can be written based on the sliding surface as

OS — -VS + OS + VS + G - t(34)

it is assumed that

ST (O -2 V)S — 0

by substituting (34) in (33)

У — 1STDS-STVS + ST(OS + VS + G -

• t ) — S^T(OS + VS + G - t)

Suppose the control input is written as follows

̂= ̂ +1̂s=[Î1( ̂+ ̂)+ ̇] ̂+

К . sgn ( S )+ K_US

By replacing the equation (37) in (36)

̇=S1 (Ḋ+VS +G-̂ ̇- ̂S- ̂-

K„S - Ksgn (S)=ST.̃ ̇+ ̃s+ ̃- k„s - Ksgn (S)/

It is obvious that

|̃ ̇+ ̃S+ ̃-K„S|≤|̃ ̇|+| ̃S|+

| ̃|+| K„S |

The Lemma equation in robot manipulator system can be written as follows

K_u =[|̃ ̇|+| VS |+| G |+| K„S |+ в ] , i (40) =  ,2,3,4,…

The equation (35) can be written as

K_u ≥|[ ̃ ^̇+ VS + G ^- K_yS ]|+4i          (41)

Therefore, it can be shown that

̇≤-∑4i | St | i=l

Consequently the equation (42) guaranties the stability of the Lyapunov equation.

Fuzzy Inference Engine: This section provides a review about foundation of fuzzy logic based on [3253]. Supposed that и is the universe of discourse and x is the element of и , therefore, a crisp set can be defined as a set which consists of different elements ( x ) will all or no membership in a set. A fuzzy set is a set that each element has a membership grade, therefore it can be written by the following definition;

A ={ x , Ha ( x )| x ∈ X }; A ∈ U (43)

Where an element of universe of discourse is X, Ца is the membership function (MF) of fuzzy set. The membership function ( M'A (X)) of fuzzy set A must have a value between zero and one. If the membership function M'A (X) value equal to zero or one, this set change to a crisp set but if it has a value between zero and one, it is a fuzzy set. Defining membership function for fuzzy sets has divided into two main groups; namely; numerical and functional method, which in numerical method each number has different degrees of membership function and functional method used standard functions in fuzzy sets. The membership function which is often used in practical applications includes triangular form, trapezoidal form, bell-shaped form, and Gaussian form.

Linguistic variable can open a wide area to use of fuzzy logic theory in many applications (e.g., control and system identification). In a natural artificial language all numbers replaced by words or sentences.

If - t ℎ en Rule statements are used to formulate the condition statements in fuzzy logic. A single fuzzy If - t ℎ en rule can be written by

If x is A Then у is В (44)

where A and В are the Linguistic values that can be defined by fuzzy set, the If - part of the part of “ x is A ” is called the antecedent part and the t ℎ en - part of the part of “ у is В ” is called the Consequent or Conclusion part. The antecedent of a fuzzy if-then rule can have multiple parts, which the following rules shows the multiple antecedent rules:

if e is NB and t ̇ is ML then T is LL (45)

where e is error, ṫ is change of error, NB is Negative Big, ML is Medium Left, T is torque and LL is Large Left. If - t ℎ en rules have three parts, namely, fuzzify inputs, apply fuzzy operator and apply implication method which in fuzzify inputs the fuzzy statements in the antecedent replaced by the degree of membership, apply fuzzy operator used when the antecedent has multiple parts and replaced by single number between 0 to 1, this part is a degree of support for the fuzzy rule, and apply implication method used in consequent of fuzzy rule to replaced by the degree of membership. The fuzzy inference engine offers a mechanism for transferring the rule base in fuzzy set which it is divided into two most important methods, namely, Mamdani method and Sugeno method. Mamdani method is one of the common fuzzy inference systems and he designed one of the first fuzzy controllers to control of system engine. Mamdani’s fuzzy inference system is divided into four major steps: fuzzification, rule evaluation, aggregation of the rule outputs and defuzzification. Michio Sugeno use a singleton as a membership function of the rule consequent part. The following definition shows the Mamdani and Sugeno fuzzy rule base

Mamdani F . R¹ : (46) у is В then z is C

Sugeno F . R¹ :

у is В then f ( x , У ) is C

When X and У have crisp values fuzzification calculates the membership degrees for antecedent part. Rule evaluation focuses on fuzzy operation (AND /OR ) in the antecedent of the fuzzy rules. The aggregation is used to calculate the output fuzzy set and several methodologies can be used in fuzzy logic controller aggregation, namely, Max-Min aggregation, Sum-Min aggregation, Max-bounded product, Max-drastic product, Max-bounded sum, Max-algebraic sum and Min-max. Two most common methods that used in fuzzy logic controllers are Max-min aggregation and Sum-min aggregation. Max-min aggregation defined as below

Ни ⁽ Хк , Ук , и )= и ⋃ ^Ti=l^{FRi (} х_к , Ук , и )            (47)

=     2min']0 U^Rpq ( Хк , Ук ), Ир_т ( и )13

The Sum-min aggregation defined as below

Ни ( х_к , Ук , и )= и ⋃ Ci^FR' ( х_к , Ук , и )           (48)

=∑minr₌₁ 0 ^^Rpq ( Хк , Ук ), Нр_т ( и )1

where Г is the number of fuzzy rules activated by Xr and Ук and also fl и Li^FRt ( Хк , У к , и ) is a fuzzy interpretation of i - t ℎ rule. Defuzzification is the last step in the fuzzy inference system which it is used to transform fuzzy set to crisp set. Consequently defuzzification’s input is the aggregate output and the defuzzification’s output is a crisp number. Centre of gravity method ( COG ) and Centre of area method ( СОА ) are two most common defuzzification methods, which COG method used the following equation to calculate the defuzzification

СПС           ^∑ _tU_t ^∑ /=1 . Ни ( Хк , Ук , U_t )      (49)

( ,  )= _∑ ^∑ й . Ии ( х_к , Ук , , ₎

and СОА method used the following equation to calculate the defuzzification

СОА ( х_к , Ук )

^∑ jUj . Ии ( Хк , Ук , ^ ) ^∑ tHu .( х_к , Ук , Ui )

Where COG ( х_к , Ук ) and СОА ( х_к , Ук ) illustrates the crisp value of defuzzification output, U / ∈ и is discrete element of an output of the fuzzy set, Ци .( Хк , У к , U[ ) is the fuzzy set membership function, and г is the number of fuzzy rules.

Based on foundation of fuzzy logic methodology; fuzzy logic controller has played important rule to design nonlinear controller for nonlinear and uncertain systems [53-66]. However the application area for fuzzy control is really wide, the basic form for all command types of controllers consists of;

• •    Input fuzzification (binary-to-fuzzy[B/F]conversion)

• •    Fuzzy rule base (knowledge base)

• •    Inference engine

• •    Output          defuzzification          (fuzzy-to-

• binary[F/B]conversion).

• III.    Methodology

First part is focused on eliminate the oscillation (chattering) in pure SMC based on linear boundary layer method. To reduce or eliminate the chattering it is used the boundary layer method; in boundary layer method the basic idea is replace the discontinuous method by saturation (linear) method with small neighborhood of the switching surface. This replace is caused to increase the error performance [20-24].

в(t)={х,|S(t)|≤∅};∅>0

Where ∅ is the boundary layer thickness. Therefore, to have a smote control law, the saturation function Sat ( s ⁄) added to the control law:

и=  (⃗⃗, t). Sat .S ⁄∅/

Where Sat. ⁄/ can be defined as sat .5 ⁄∅/

⎧ ¹        (⁵⁄ _∅ >1)

_=⎨ ⎪ _-¹       .⁵⁄ _∅ <1/

⎩^{⎪ s} ⁄ _∅     (- ^{1< 5}⁄_∅ <1)

Based on above discussion, the control law for a robot manipulator is written as [10-24]:

U=    + UT(54)

Where, the model-based component и eq is the nominal dynamics of systems and U_eq can be calculate as follows:

Ueq=[D"1 (f+C+G)+ ̇]D(55)

and Usat is computed as;

^sat =   ∙ sat .5 ⁄∅/

The control output can be written as;

U=    +К. sat .5 ⁄∅/

( Ueq + К . sgn (S) ,|S|≥ ∅

={ Ueq + К .⁵⁄ _∅     ,|S|< ∅

Second step is focused on design fuzzy estimation variable structure based on Lyapunov formulation. The firs type of fuzzy systems is given by

f ( x )= ∑ ihe^l8^l ( x )= 9^TE ( x )            (58)

Where о =(01,…,0м)т,ℰ(х)=

(ℰ ¹( X ),…,ℰ м ( X )) т _, and ℰ¹( X )=

1^.1 ^{( Х}1 ⁾

:∏7=1 1 ∑ Г=1(∏ 7=1 дл! (Xi)).      О1,…,дм are adjustable parameters in (58). Цд! (Х-^),…,Цд™ ( хи ) are given membership functions whose parameters will not change over time.

The second type of fuzzy systems is given by

/( X )                                              (59)

^∑ ив¹ [∏" i ехр(-4 х. - "15)]

^∑  [∏ ^?-^ехр (-4 . - ^5)]

Where 6¹ , a- and 5- are all adjustable parameters. From the universal approximation theorem, we know that we can find a fuzzy system to estimate any continuous function. For the first type of fuzzy systems, we can only adjust О¹ in (58). We define / ^ ( х | 6 ) as the approximator of the real function/( X ).

/ ^ ₍ X | 6 )= 6^ТЕ ( X ) (60)

We define 6 ^∗ as the values for the minimum error:

о ∗₌ arg min [sup | f ^ ( x | О )- g ( X )|]        ⁽⁶¹⁾

^{9 ∈} a l_x ∈ и                    J

Where П is a constraint set for 6 . For specific X , sup_{x ∈} и | f ^₍ X | 9 ^∗)- f ( X )| is the minimum approximation error we can get.

We used the first type of fuzzy systems (59) to estimate the nonlinear system (48) the fuzzy formulation can be write as below;

f ( X | 9 )= 9^te ( x )

^∑7=i #' [ g_Ai ⁽ X )] =_∑7=1[ g_Ai ( X )]

Where o¹ ,…, 9^U are adjusted by an adaptation law. The adaptation law is designed to minimize the parameter errors of 6 - 6 ^∗. A fuzzy system is designed to compensate the uncertainties of the nonlinear system. The control input is given by

T= ^{^} ̈ + C ^{^} ̇ + G - F ^₍ s )- Fcp ( s ) (63)

Where F ^₍ s )=[ fi ^₍^si ),…, f ^₍ ^m )] T and ^cp ( S )= [ ^cpl (⁵1),…, Fcp_m ( ^m )] T . We define F = Δ M ̈ + Δ Ci ̇ r + Δ G where F =[ fi ,…, fm ] T , Δ M = - M , Δ Cl = ^{^-} Cl and Δ Ci = - G .

From Universal Approximation Theorem in (61), there exists an optimal fuzzy controller f ^ ^∗( Sj ) such that:

fj =   ^∗₍ e , ̇)+ Δ/

Where Δ I is the minimum approximation error.

The fuzzy if-then rules are given by fuzzy rule base. In (62), we assume ∑ L=ig_A^ ( e ,ṫ)=1 and ^£j ( e , ̇) becomes

,             ^^Aj ^(e, ̇)                              (65)

=1 ⁽ )= _∑ L=1 _[ g^ ( e , ̇)]^{=     (e} , ̇)

Where we define ^ =    (e,ṫ). The membership function ^al- (e, ̇) is a Gaussian membership function represented by g^ ( sj)=exp[-( ffj ((e,e )̇ - a1-))2 ]          (66)

Then the fuzzy estimator f^(e,ṫ) is given as f^ (e, ̇)= ^Vj                          (67)

where 9j =[ ⁶i ,…, 9^ ] т , =[ ^ , Vj ,…, _Фу ] t .

We define such that

̃ 'j =    ^- f ^ ₍ e , ̇)

= ^∗₍ e , ̇)- f ^{^ (} e , ̇)+ Δ /

= ^{∗ T<}? ^- ^Vj +Δ i                  (68)

where 6 ^∗ and Ф ^∗ are the optimal values based on Universal Approximation Theorem in (61). We define ^̃ =  ^∗-   , ̃ =  ^∗-     is rewritten as

̃ j =( ⁹i + ^̃ j )( + ̃7)- ^бТ]Ф) +Δ =   ̃ j + ^{̃ Т},Ф] + ^̃ J ̃ j +Δ

We take Taylor series expansion of Ф] around vectors aj and where aj =[ «I ,…, a^ ] T a_}- =[ ^al ,…, ^аГ ] T ( aj and a- are defined in (66)):

вф:     дф:

Ф ∗₌ ^7 +     ̃ +     ̃ j + h . о . t .

J * da, * da, *

two and

where   ̃ j =    ^- aj , ̃ ₇- =    ∗ - ^j and ℎ. о . t .

denotes the higher order terms. We rewrite (70) as

Эф;

̃ =    ̃ +

* da; *

Эф!

_̃ + h . о . t . daj ^J

=   ̃+ Cj ̃+ h . о . t .

where

	⎡	м	⎤	(72)
	⎢	да/ '	да/	⎥
	⎢	8ф]		⎥ ⎥
=	⎢ ⎢⋮	daj	да/	⎥ ,
	⎢ ⎢	8ф1	ЭфУ	⎥ ⎥
	⎣	daf ’	⎦
	⎡	м	⎤
⎢	да/	да/ '	⎥
⎢ ⎢	у	8ф]	⎥
= ⎢ ⎢	да/	daj	⎥ ⎥
⎢ ⎢	⋮	дф]	⎥ ⎥
	⎣	да^ ‘	⎦

where     ,    , and     are positive constants;

=[  ,   ,…,   ]    ,      =[  ,   ,…,   ]    ,

=[  ,    ,…,   ]   ;     ,     are given in (72);

( ) is the compensation term defined in (63).

If the following Lyapunov function candidate defined by:

=      +

_{∑   (} ̃ ₊ ̃ ̃ ₊ ̃ ̃ ₊ ̃ ̃

2^ZjJ-¹\ljjl Ч;₂    4,3    Ч₇4

The derivative of is defined by:

̃ ̃̇

̇=    ̇+    ̇  +∑  (   ++

2              7   \ Ч71Чу2

̃ ̃̃ ̃

+

ЧуЗ    Чу4

We substitute (71) into (69):

̃ =   (  ̃ +  ̃ + . . .)+ ̃+

̃ ̃ +Δ

=    ̃ +   ̃ + ̃+

. . .+ ̃ ̃ +Δ

=    ̃ +   ̃ + ̃+ where = ℎ. . .+ ̃ ̃ +Δ is assumed to be bounded by |  | ≤   . is a constant and the value of uncertain to the designer. We define ∗ as the real value and the estimation error is given by

̃ =  ^∗-                                  (74)

Third step is focused on design fuzzy (antecedent and consequent) adaptive fuzzy estimation sliding mode based on Lyapunov formulation. We produce an adaptation law to online tune the following parameters:

in (64),   , in (66) and the bound in (74). The adaptation laws are expressed as

where ^̃ =  ^∗-    , ^̃ =  ^∗-    , ̃ =  ^∗-

,  ̃ =  ∗-     . from robot manipulator formulation and (1):

() ̈+   ( , ̇) ̇+  ( )=  ^{^} ̈ +       (82)

^ ̇  +  ^-  ^()-    ( )

Since ̇-     is a skew-symmetric matrix, we can get    ̇+    ̇  =   (  ̇+    ). From

̇  = ̇-  = ̇  - and ̈ =  ̈- ̇=  ̈ -  ̇

̇+    =  - ^{^}()-    ( )           (83)

where =Δ ̈ +Δ ̇ +Δ   , Δ =  ^-

, Δ =  ^- and Δ =  ^-   . Then ̇ becomes

̇=   (  ̇+   )+∑   4 ^{̃ ̃̇} + ^{̃ ̃̇} +

\ Ч]1     Ч]2

̃ ̃   ̃ ̃

+

ЧуЗ    Чу4

=  ( - ^()-   ( ))+

∑  4

̃̃  ̃̃

+   ++

Ч71    Ч72    Ч73Ч

= ∑    ( - ^ ( )-   )+

6j = Tlj2Sj ф.	(75)
«j = Ч7 s$j Bj в.	(76)
Оу- = j] jsS j Св dj	(77)
fepi (S у')   ВjS gn^s^	(78)
Ej = j y i |S j |	(79)

∑

̃  ̃̇ ̃  ̃̇

̃ ̃ ^̇     ̃ ̃ ^̇

+   +   +

Чу! Чу 2 ЧуЗ Чу4

=∑   (   ̃+   ̃+ ̃  + -

)   ∑

=∑  [ ̃ (

^̇ )+ ̃ (

)

̃̃  ̃̃

+   ++

Ч71    Ч72    Ч73Ч

-

^̇ )+ ̃ (

- ^̇ )]+∑  (

-

-

We substitute the adaption law (75)-(79) in to (84):

V = TgU^jS) - SjEjSg((S)) - £) |S ) |] m

= ∑[   -      ( )-( ∗(85)

-   )      ()]

7П

=∑[   - ∗    ()]

7=1

=∑[|  ||  |-  ∗||]

=∑  [|  |(|  |- where     is negative semidefinite . We define

^̇ =|  ()|(|  |-   ^∗ ) . From ^̇ ≤0 , we can get ()

is bounded. We assume |  ()|≤ and rewrite

|  ()|( ^∗ -|  |)≤- ̇ as

()≤   |  ()||  |-   ̇  ≤   ||-

∗                   ∗         ∗

̇

∗

Then we take the integral on both sides of (86):

∫ |  ()|   ≤ ∗ ∫ |  |   + ∗.()-

()/≤ ∗ ∫ |  |   + ∗(|()|-

|()|)

If ∈   , we can get ∈ from (87). Since we can prove ̇ is bounded (see proof in [15]), we have ̇ ∈    . We introduce the following Barbalat 's

Lemma[16].

Lemma: let ∅:  → be a uniformly continues function on [0, ∞) . Suppose that     →  ∫ ∅()

exists and is finite. Then,

→ ∅ ()=

Therefore, by using Barbalat ^'s Lemma, we can get _→  ()=0 and    _→  ()=0 .

• IV.    Results

This methodology can online adjust both the premise and the consequent parts of the fuzzy rules. In this method we choose ^̂,B^̂ andC^̂ for compensation. We define five membership functions for each input variable based on

( )=    [-(  (  -  ))]            (88)

Sliding mode controller (SMC) and proposed fuzzy (premise and the consequent) adaptive fuzzy estimator sliding mode controller were tested to sinus response trajectory. The simulation was implemented in Matlab/Simulink environment. Link/joint trajectory and disturbance rejection are compared in these controllers. These systems are tested by band limited white noise with a predefined 40% of relative to the input signal amplitude.

Link/joint Trajectory: Figure 1 shows the link/joint trajectory in SMC and proposed methodology without disturbance for sinus trajectory. (This techniques is applied to first two link of continuum robot manipulator)

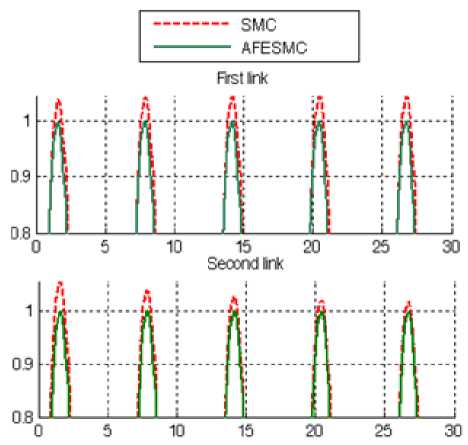
Fig. 1: Proposed method (AFESMC) and SMC trajectory: applied to continuum robot manipulator

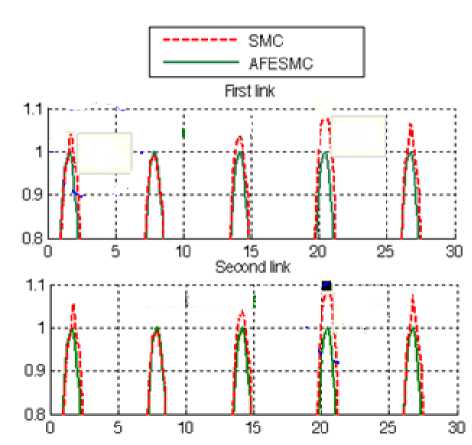
Fig. 2: Proposed controller (AFESMC) and SMC trajectory with external disturbance: applied to robot manipulator

By comparing sinus response, Figure 1, in SMC and proposed controller, the proposed controller’s overshoot (0%) is lower than SMC's (3%) .

Disturbance rejection: Figure 2 is indicated the power disturbance removal in SMC and proposed controller. Besides a band limited white noise with predefined of 40% the power of input signal is applied to the sinus SMC and proposed controller; it found slight oscillations in SMC trajectory responses.

• V.    Conclusion

In this paper, a fuzzy (premise and consequent) adaptive robust control fuzzy estimator sliding mode method is proposed in order to design a high performance robust controller in the presence of structured uncertainties and unstructured uncertainties. The approach improves performance by using the advantages of sliding mode control, fuzzy logic estimation method and adaptive control while the disadvantages attributed to these methods are remedied by each other. This is achieved without increasing the complexities of the overall design and analysis of the controller. The proposed controller attenuates the effort of model uncertainties from both structured uncertainties and unstructured uncertainties. Thus, transient performance and final tracking accuracy is guaranteed by proper design of the controller. The results revealed that adaption of fuzzy rules weights reduce the model uncertainties significantly, and hence farther improvements of the tracking performance can be achieved. This algorithm created a methodology of learning both the premise and the consequence part of fuzzy rules. In this method chattering is eliminated.

Acknowledgment

The authors would like to thank the anonymous reviewers for their careful reading of this paper and for their helpful comments. This work was supported by the SSP Research and Development Corporation Program of Iran under grant no. 2012-Persian Gulf-3C.