On nonparametric algorithms of object groups control

Introduction. The paper is devoted to control of a group of static and dynamic objects in conditions of both parametric and nonparametric indeterminacy. The identification problem is one of the major ones in the control theory and is also closely related to the amount of information a researcher has at the stage of setting appropriate identification tasks. The control of a group of objects should be based on the following principles:

– collection of a priori information and analysis of current information about the process under investigation;

– mathematical formulation of the problem, assuming certain assumptions;

– synthesis of appropriate control algorithms.

The classical control problem. At first the control task is considered in the standard setting [1]. The task is viewed as a certain local object (fig. 1).

----* ----* *

parametric setting. Here u s , x_s , ц _s are temporal vectors

----*                                                     ----*                                                      *

equal to Xs  = (xi, x2, ..., xs), us  = (u 1, u2, ..., us),

= (µ 1 , µ 2 , …, µ s ) respectively [3; 4]. Nonparametric models are commonly expressed by the following formula:

xsl (u, ц) = sn

Z x i- П ф

= 1 j = 1

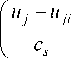
A m П ^ф ) j = 1

ц j -Ц ji c_s

snm

£П ф|- j --²^| П ф|^ц2-^ц ^ I i = 1 j = 1 V c s ) j = 1 к c s )

l =1, k and control algorithms will be expressed like this:

^usl ^{( x} , ц ) =

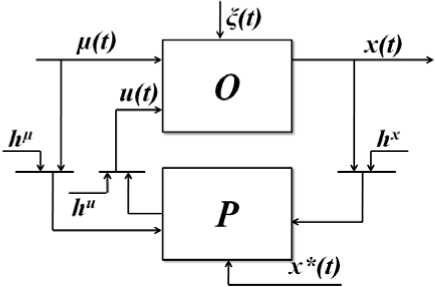
Fig. 1. The general control scheme

sk

Z№

i = 1 j = 1

Рис. 1. Общая схема управления

The fig. 1 shows the following designations: О is an object, Р is a regulator, u ( t ) = ( u ₁( t ), ..., u n ( t )) Q( u ) c R n , x ( t ) = ( x i ( t ), ..., X n ( t )), Q( x ) c R k , ц( t ) = (Ц 1 ( t ), ..., ц n ( t )), О(ц) c R m , the input variable ц( t ) is monitored, but not controlled, x* ( t ) is a setting impact. Random perturbations h^u , h ^µ, h^x are errors in the measurement of variables, and ξ( t ) is the random perturbation affecting an object. The scheme has a local character [2]; further all random variables will be omitted for simplicity. In identification of such objects the models can have the following appearance: X ( u , ц) = F ( u , ц, a) is in case of a parametric setting, or x s ( u , ц) = S ( u , ц, u s , x s , ц _s ) in case of a non-

sk

Z u ,П ф i = 1 j = 1

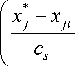
m

Пф j=1

ц у -ц у, c_s

' ^x *-^- x ji Iv m r ф( ^ц у 2^ц у

_V    c s     ) J = 1    V     c s    .

l = 1, n.

Groups of objects. Further on groups of objects will be considered, in particular the simplest of them is a group of serial objects shown in fig. 2. For simplicity, random perturbations acting in channels of measurements and affecting an object are not presented any more, though they are surely present.

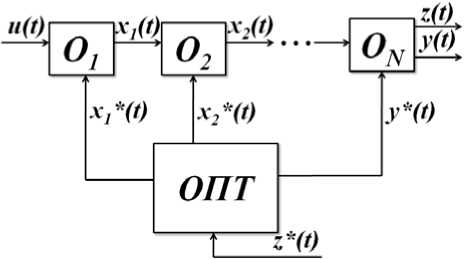
Fig. 2. The scheme of serial objects

Рис. 2. Схема последовательных объектов

Here О 1 , О 2 , ..., О N objects are shown in a general view and each of them may contain the macro object shown in fig. 1, where ОПТ is the optimizer. X 1 * ( t ), x 2 * ( t ), ..., x N * ( t ), y* ( t ) are controlling variables for the optimizer. The purpose of the optimizer is to find the controlling impacts x ₁ * ( t ), x ₂ * ( t ), ... , x_N* ( t ), y* ( t ), for achieving z* ( t ) ≈ z ( t ). Z( t ) is the most important output variable which characterizes the result of the work of the whole group of objects. It is important to note that the discreetness of measurements z ( t ), y ( t ) and x ( t ) can significantly differ. Therefore the accelerated forecast z ( t ) is often used in such systems; it is this value that creates the cost of the final product. The measurement discreetness z ( t ) is the greatest of all variables and can be equal to days, weeks, and sometimes reaches a month. The optimization task takes the following form:

Г1

R = м JE^f^ u, Ы,(3)

I i=1

where W ( ∙ ) function is an analog of Φ( ∙ ), and γ vp coefficients are a peculiar analog of the blur coefficients playing the role of weight factors in this case [5].

The parallel-serial scheme (fig. 3) of technological devices interaction which is often met at the enterprises of a discrete-continuous type is more complicated [6–8].

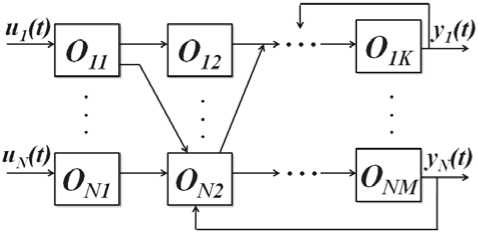
Fig. 3. The parallel-serial objects scheme

where R is a utility function; f ( x , u ), = 1, k , is a set of quality criteria which are created on the basis of the model of the researched process x = φ(µ, u ), = 1, k ; in their turn, φ , = 1, k are continuous functions; α is a weight factor which is defined by the decision-maker.

The following restrictions were adopted in the utility function:

Рис. 3. Схема параллельно-последовательных объектов

M ^ { ф ( ц , u , ^ ) } > 0, J = 1, X,

M ^ { ф ( ц , u , ^ ) } = 0, j = 1, G ,

where ξ is random perturbations with unknown probability density P (ξ).

Then the algorithm of computation u^j p , j = 1, m , can have the following appearance:

u j = — p _s

s

E u/ a tps

E a,_n. tps

i = 1

a_t = П ф| f v ^{( Ц}7 u t ⁾ | П ф| f v ^{( Ц} t , ^Ц v ^{) tp}s       I J 11 ^

v = 1    V     c s     ) v = 1 V      c s

The following designations are accepted in the fig. 3: N is a number of process lines; all designations of technological variables are excluded for simplicity, generally the emphasis is placed on communication of technological chains.

Finally, an interdependent technological process illustrated in fig. 4 is the most complicated one.

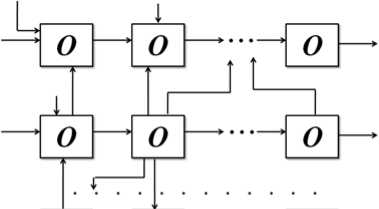
Fig. 4. The scheme of interdependent objects

Рис. 4. Схема взаимосвязанных объектов

v х П Ф j = 1

( ^ J ⁽ ц t , ut )

I c^T V c s

sng Ф J ( Ц t , u_t ⁾

.

c ^Ф

In case of appearance of a decision-making problem, algorithms (5), (6) can be slightly changed. It is caused by the fact that in this case it is necessary to consider learning selection limitation and as a result of it the absence of blur coefficients aspiration to zero with the increase of s . In this case it is more expedient to present the algorithm of decision-making (6) in the following form:

km atps =П W (yvp ■ fv (^t, ut ) )П W (yvp ■ (^v "^V ) )X

V=1

vX хП W ( yvp ■ ^j (^t, ut ))П sng ф j (^t, ut x j=1

The most important here are technological communications between industrial facilities, which are not described separately in the paper. Any technological variables are not described as well [9].

Similar processes are also met in the active systems. Researchers have paid much attention to them lately. Active systems include processes with involvement of a man or a group of people in any field of activity. Typical features of such processes are incompleteness of a prior data, uncertainty, mutual connectivity, difficulty of formation of the agreed targets and methods of their achievement. Incompleteness of a priori data results in the necessity to formulate these or those tasks of local character in a variety of essentially different settings, and their combining in a single system presents serious theoretical difficulties. The general scheme of the active process is presented in fig. 5.

Here λ( t ) is a variable which may be known to the researcher, but it is hardly measureable, i. e. its control takes place rather seldom and the procedure of measurement is long and expensive. The variable Θ( t ) is responsible for the impact on an object of external environment. For organizational systems such impact can include any instructions, resolutions, orders, acts wh ich undergo these or those changes eventually. ω ⁱ ( t ), i = 1, k , are the process variables monitored along the object length which show additional information about the process. Θ t , µ t , u t , ω ⁱ t , x t , y t , z t are measurements of the appropriate variables which are carried out through different intervals of time.

At present two fundamental differences between organizational systems and technical ones are revealed. The first difference is the existence of back couplings, control circuits, etc., built in the researched process from outside. The second difference is characterized by monitoring aids or measurement of the appropriate variables, as one of elements of gauges of some input-output variables characterizing a process status is a person or a group of experts. The estimates of some variables are impossible without involvement of a person; therefore there will be a subjective factor in measurements. The control system of organizational processes is a hierarchical, multiple-loop system including a person as a necessary and major element; in this case the formation of a matrix of observations is of some difficulty as it includes variables of different types belonging to different scales. One more cornerstone in active systems control is ignorance about the process that leads to the mismatch between the assumptions of the researched object and the object itself. It happens because of a lack of a priori information, influence of arbitrary factors whose characteristics are not known to the researcher, imperfection of monitoring aids of variables, and not enough representativeness of sampling for measurements [10–13].

An object group which is widespread at thermal power plants will be considered as an example (fig. 6).

It should be noted that objects О 1 , О 2 , ..., О N are boiler units, T ₁, T ₂, ..., T_L are turbines which can be in different statuses up to switch-off in production. It naturally significantly complicates the control task of such an interdependent complex. Similar systems are at a development stage at present time [14; 15].

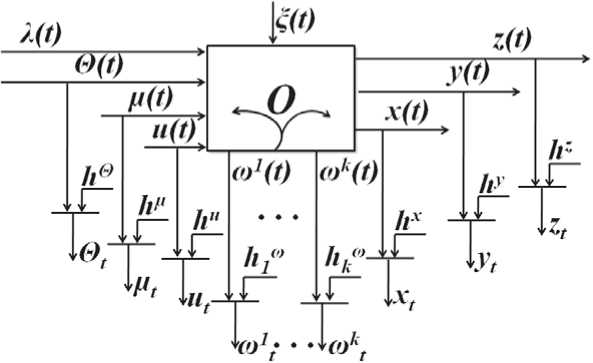
Fig. 5. The general scheme of a multivariate active process

Рис. 5. Общая схема многомерного активного процесса

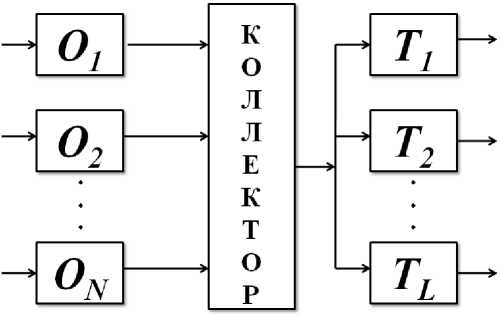
Рис. 6. The general scheme of a power unit of a thermal power plant.

Рис. 6. Общая схема энергоблока теплоэлектростанции

It seems reasonable to provide some data on mathematical simulation by concentrating metallurgical conversion NMMC which passed numerous tests and was implemented in production. The fragment of a similar technological chain is presented in fig. 4. In this case the initial variables were technological parameters of the ores extracted in the territory of the Norilsk industrial region (Oktyabrskii, Komsomolskii, Medvezhii ruchey and others) as well as the amount of furnace charge, sandstone, concentrate, waste, matte and others and contents of different elements in them. The similar system which was called “Metal” system was implemented at Norilsk MMC with considerable economic effect. K-, H-, T-models which are included in “Metal” represented a system of more than 330 ratios of parametric and non-parametric types [10].

Conclusion. The paper deals with the problem of identification and control of a group of serial, parallel and parallel-serial type of technological objects sequences. The special features of the relationships between objects and process variables in each case are defined. Algorithms of identification and control of a group of objects, as well as the decision-making algorithm are given in a general form. Examples of technological processes representing groups of local objects are described.