On nonparametric control of a dynamic system

Introduction. The problem to be solved in the paper is the design and implementation of nonparametric control algorithms. An object under control is assumed to be inertia-free and it is described by an equation with an unknown structure with respect to its parameters. Together with the control effect the object is influenced by uncontrollable but observable input. The nonparametric dual control algorithms under consideration were investigated for various tactics of determining the bandwidth parameters at each clock cycle. A concept of dual control was created by A. Feldbaum [1] and developed by Y. Tsypkin [2]. It was originally intended for Bayes control problem statement when the object under control was inertia-free. The main idea of the concept was simultaneous control and learning of the object. That involves procedures of parametric identification [3] together with implementation of control methods in the parametric formulation [4–7]. It should be noted that a dual control system is an example of a control device with memory.

Problem statement. The following notations are introduced: let x = ( x 1 ... x n ) e R n be output of the object, u = ( u 1 ... u k ) e R k be controlled input effect, ц = ( ц 1 ... ц m ) e R m be uncontrollable but observable input, and x * = ( x * ... х П ) e R n be reference of the object under control (fig. 1) [8].

In fig. 1 the control device is denoted by ‘ yy ’, the object under control is denoted by ‘ О ’, and random stationary noise effects influencing both the object itself and the object measurement channels are denoted by ^ _t , h_t . We assume these noise effects to be unbiased and to have limited variance. The unknown model curve of the object x = f ( u , ц ) is assumed to be one-to-one with respect to control effect u eQ ( u ) e R^k for the fixed vector ц e О ( ц ) e R m in the feasible domain of u e Q ( u ) .

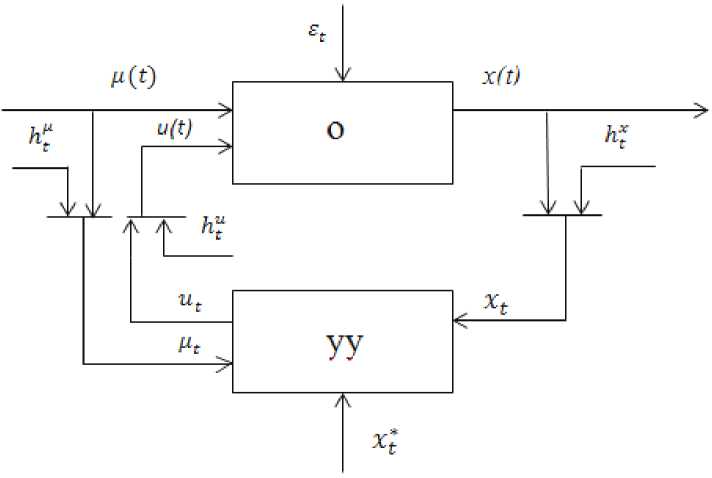
Fig. 1. The scheme of a nonparametric control system, where ( t ) denotes continuous time, and the subscript t indicates discreet time moments of measurements

Рис. 1. Схема непараметрической системы управления: t – непрерывное время; t в качестве индекса – дискретное время контроля измерения

Nonparametric combined control algorithms. A nonparametric control algorithm is based upon Nadaraya and Watson [9] nonparametric estimates of regression. A nonparametric dual control algorithm in the form [10] for a single-input case is represented by the expression:

ut + 1 =

t

Z ф

i = 1

t

Z u ф i=1

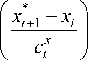
ц t+1 -ц i с ц ct

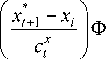
( ц t + 1 -ц ) l с^ц J V ct J

+ A u_{t + 1}, i = 1, t .

For the multiple-input object a nonparametric dual control algorithm can be expressed by

n ut+1 = tn

Z u ⁿ№ i = 1 j = 1

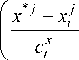
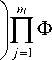
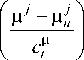
tn

ZП Ф i = 1 j = 1

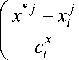
A m

Пф

J j = 1

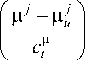
^+A ut + 1 , (2)

c t = ¹ 2 |^ц t + 1 ^цр| , ⁽⁵⁾ where l ₂ is a coefficient to be found experimentally: l 2 >  1. ц 0 is found from the optimization process ц 0 = min |ц —ц i |, i = 1, p . Finally we get a new reduced data set { x i , u i , ц i } , i = 1, 5 , whose size 5 satisfies the inequality 5 < p .

Judging from our experience, the algorithm (1) is insensitive to the sequence of c t and c f bandwidth parameters fitting.

Let us pay attention to learning process of the nonparametric dual control algorithm. It was discussed in [10], and is represented by the iterative scheme:

^ut + 1 = ^u * ^{+ A u}t + 1 . ⁽⁶⁾

Information about the object under control is contained in u_t ^* , and learning capabilities are fulfilled by the search additive A u_{t + 1}:

^A u t + 1 =a ( ^x * _{+ 1} ^- x t + 1 ) , ⁽⁷⁾ where a is a coefficient defining search amplitude that should be fitted. We require that A u_{t + 1} ^ 0 with the growth of t .

It is a well-known fact that the output of a discrete dynamic object can be represented as follows [3]:

^xt = ^{f ( x}t - 1 ... ^xt - k , ^ut ^{). (8)}

In this case x_t - 1 ... x_t - _k can be interpreted as supplementary incontrollable inputs in terms of previously introduced static object modeling routine. Fig. 2 describes the approach.

In fig. 2 the following notations are given: x_t ^* is a reference output variable of the object; t with round brackets is a continuous time variable; subscript t denotes discrete time indices; h_t^u , h_t^x are random noise in measurement channels corresponding to the variables of the object; ^ ( t ) is an unobservable random effect.

Thus, for the uncontrollable but observable variable x_t - i , i = 1, k as the input effect of the object the algorithm (1) can be rewritten in the following form [15]:

^ut + 1 =

t

Z ^ф i=1

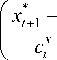
k

П ф | t^{^} - j j = 1 V

^xi - j

t

ZФ i=1

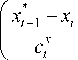
k

ПФ j=1

+ A u_{t + 1}, i = 1, t .

A general control theory of similar objects control is explicated in [2]. Implementation of the corresponding dual control algorithms can be found in [16; 17]. Below we will focus on numerical experiments with a nonparametric dual control algorithm (9). During the experiments the object under control will be substituted by either an inertia-free (memory-free) operator or a dynamic operator.

It should be noted that the control algorithm does not possess information on the equation (operator) of the object under control excepting the type of the operator. The use of dual control algorithms is presented in [16; 17].

Numerical experiments. To perform the first batch of numerical experiments the object was substituted by the expression xt+1 ut+1 + ц t+1 ,

where x(t) is an output variable; u(t) is a controllable input; μ(t) is observable but uncontrollable effect, taken as the process цt = 0.5 + 0.3sin(0.21).

The control procedure starts with the first point ( x 1 , u 1 , ц 1 ). Further data accumulation results in active learning of the control algorithm. As a consequence the object can be more effectively driven to a reference state or follow a reference trajectory.

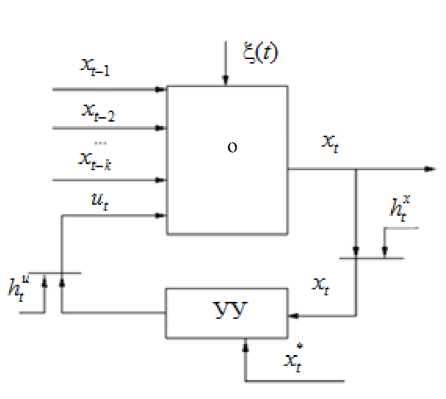
Fig. 2. A control scheme for an object with memory (dynamic object)

Functioning of a nonparametric control algorithm is illustrated by fig. 3 and 4. A particular experiment was conducted to demonstrate the ability to follow the stepwise reference trajectory х* ( t ).

Fig. 4, a shows an enlarged scale of reference х* ( t ) and control x ( t ) processes depicted in fig. 4, b . A nonparametric dual control algorithm can effectively solve the control problem even for a noticeable level of noise. The case when random noise with amplitude up to 3 % of the output value is presented in fig 5.

Let the reference to the control process be given by the expression x * = 2 + sin(0.1 t ). For the case the corresponding control process is depicted in fig. 6.

Except stepwise functions and continuous reference functions one can construct other references using even random functions. To illustrate capabilities of the control algorithm (1) to follow random reference the following experiment was carried out (fig. 7). x_t ^* is defined here as a sequence of sine function and purely random effect evenly distributed in the interval [0.5; 2.5].

Рис. 2. Управление объектом с памятью

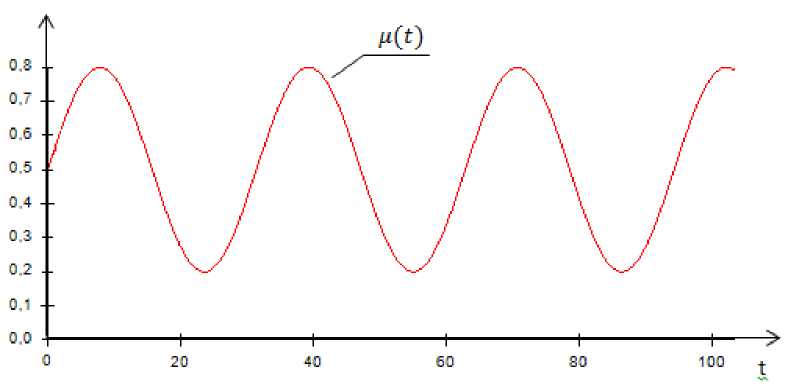
Fig. 3. Uncontrollable effect μ( t )

Рис. 3. Неуправляемое входное воздействие

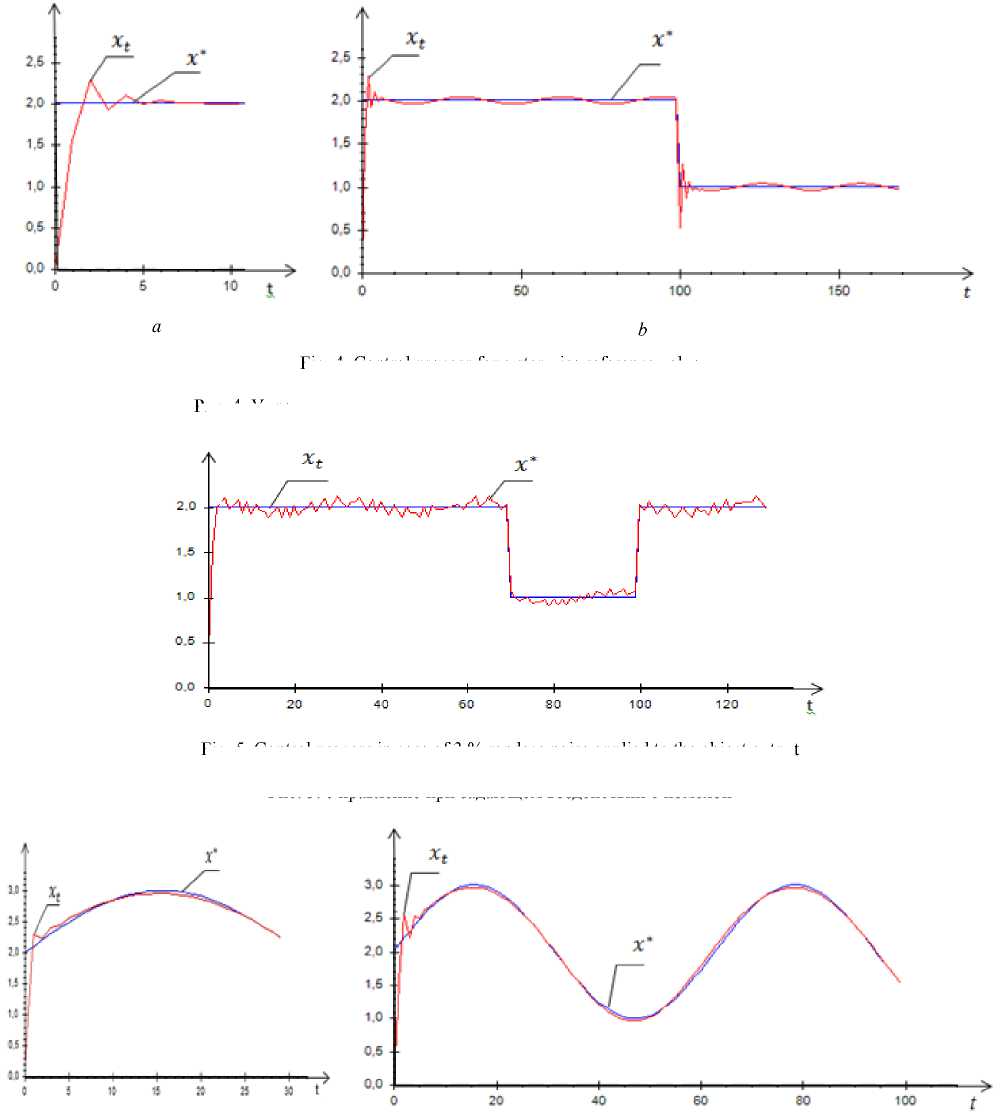
Fig. 6. Control process for continuous reference

Fig. 4. Control process for a stepwise reference value

Рис. 4. Управление при задающем воздействии в виде ступенчатой функции

Fig. 5. Control process in case of 3 % random noise applied to the object output

Рис. 5. Управление при задающем воздействии с помехой

Рис. 6. Управление при задающем воздействии в виде траектории

Experiments with the control algorithm operation make it evident that it is able to deal even with random references. On the contrary, standard P, PI, PID controllers cannot reach the level of control quality, because they are not based on data accumulation and analysis. Moreover, settling time is expected to be much worse for the controllers.

The control process in fig. 7 demonstrates satisfactory quality. That is an exceptional functionality of the control algorithm (1) can be noticed. It should be noted that none of already existing controllers can reach the same level of control accuracy and velocity.

Let us take into consideration another case when the object is represented by the dynamic operator (8). The equation is accepted in the form of the first-order discrete operator:

x t = f ( x t - 1 , u t ) .                      ⁽¹²⁾

Particularly, the linear first-order object is described by

X t =P 1 U t +P 2 X t - 1 ,                  (13)

where P 1 and P ₂ are finite constants.

For the case we describe peculiarities of the control procedure. The learning process begins with a pair of measurements, namely ( x ₀, u ₀) and ( x ₁, u ₁). The initial phase of control is devoted to data accumulation needed to bring the object to the target state. Further, time to reach the target diminishes to a great extent.

Let us demonstrate functioning of the algorithm (9). Let control reference be a stepwise function. Control process for the reference is depicted in fig. 8.

Fig. 9 demonstrates functioning of the algorithm when reference is a combination of a sine function and a random function. Again, the control process can be qualified as highly effective.

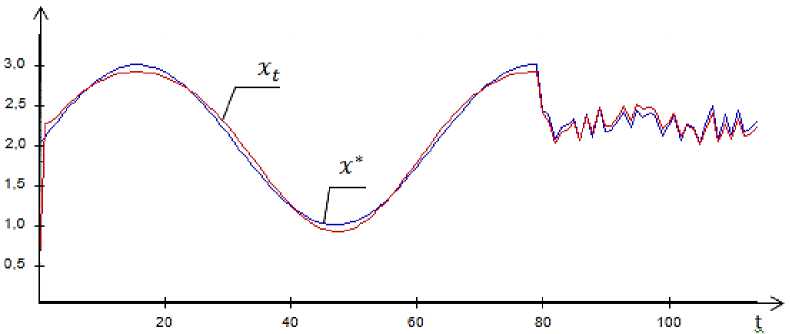
Fig. 7. Control procedure for combined reference containing random noise

Рис. 7. Управление при задающем воздействии в виде траектории и случайного задания

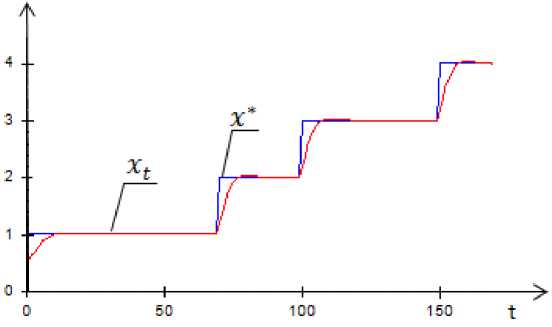
Fig. 8. Control process in case of stepwise reference

Рис. 8. Управление при задающем воздействии в виде ступенчатой функции

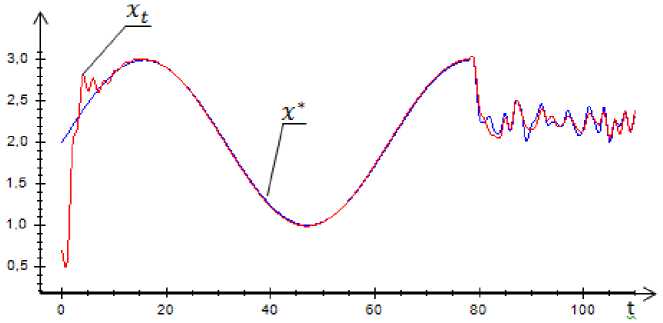
Fig. 9. A random reference test for dynamic system dual control

Рис. 9. Результаты управления при случайном задании

Thus, the algorithm (9) is able to control a dynamic object with memory, providing good quality due to data accumulation and proper model-based control synthesis.

Conclusion. The problem of dynamic system control in case of nonparametric uncertainty conditions is discussed in the paper. After re-designation of object variables this problem can be reformulated in terms of multidimensional inertia-free object control. Bandwidth determination techniques for both controllable and uncontrollable input effects are proposed. Two variants of nonparametric control algorithm learning are discussed. Illustrations of some numerical experiments with the algorithm prove that it can be used in various computer-added systems of adaptive control. The key point of the algorithm is the capability to control continuous production processes with discrete-time measurement equipment.