On nonparametric identification and dual control of quasilinear dynamic processes
Автор: Medvedev A.V., Raskina A.V.
Журнал: Сибирский аэрокосмический журнал @vestnik-sibsau
Рубрика: Математика, механика, информатика
Статья в выпуске: 4 т.18, 2017 года.
Бесплатный доступ
The problems of identification and control of stochastic objects with a discrete - continuous technological process nature under conditions of nonparametric indeterminacy are considered. This term means a situation when the process structure with the accuracy to within parameters remains unknown. A more general class of dynamical nonlinear proc- esses, later of quasilinear processes, is investigated. The processes in this category are characterized by a low degree of nonlinearity, that is the superposition principle for this type of object is insolvent. Such processes often occur in vari- ous control loops for aerospace objects and systems. Nonparametric models where the dynamic process memory depth is specified on the basis of the selection of essential variables rule are given. According to this rule, the only variables included in the nonparametric model, at which the optimum blurring factor of the kernel is minimal. Nonparametric algorithms of quasilinear objects dual control are given. Control devices built on the basis of these algorithms not only perform the object control function directly, but also its study. The case when the control device corresponding to its inverse model “turns on” at the object input is considered. The process of dual control system training with active information accumulation is analyzed. The results of a numerical study of nonparametric models for quasilinear proc- esses with memory are presented in detail, as well as the results of a computational experiment using the algorithm of nonparametric adaptive dual control. In the simulation, objects characteristics were described by equations with different degrees of nonlinearity, the form of which was unknown, and which, during active information accumulation, were automatically restituted on the basis of the input-output variables process measurement. Also, the influence of various noise levels affecting an object and in measurement channels was investigated. The given computational ex- periments confirmed the possibility of using nonparametric algorithms for identifying and controlling of quasilinear systems.
Nonparametric algorithms, nonlinear processes, blur coefficient of nuclear function, a priori information, dynamic system, dual control algorithm
Короткий адрес: https://sciup.org/148177758
IDR: 148177758 | УДК: 519.87
Текст научной статьи On nonparametric identification and dual control of quasilinear dynamic processes
Introduction. Traditionally nonlinear dynamic processes identification and control theories developed for particular classes of systems and models. In the first works on these problems the methods based on Voltaire number [1; 2] – the convolution linear integral, with its use it was possible to describe nonlinear systems, generally prevailed. It is necessary to consider that for early stages of identification for nonlinear systems methods development the noise was most often assumed by the additive white Gaussian noise [3] that was serious restriction for many relevant processes. Further other types of models were actively developed, especially important among them are block structure models, for example, a Wiener model and a Gammerstein’s model [4; 5]. This type of models consists of static nonlinear and dynamic linear elements. Also, methods based on correlation and separable functions able to define which block and structural models would be suitable for system description were developed. The basic feature of the above listed research directions is that they include a stage of a model parametrical structure choice therefore these methods are applicable only for identification and control of rather well studied processes for which the studied process equation type is in some way or other defined, for example, in the form of differential or difference equations, transfer functions, a set of standard links of a dynamic system and
others. It is necessary to consider that essential difficulties of identification and control of nonlinear objects problem solving are caused by object structure complexity and incompleteness of mathematical description and information about an object. In this case, if a priori information on the studied process is insufficient for the reasonable choice of parametrical structure, the use of nonparametric identification theory is expedient [6]. The nonparametric theory, unlike previous, assumes that only qualitative characteristics of system, such as, for example, linearity or nonlinearities, stability or instability and others are known. It means that the use of nonparametric theory allows to deviate, completely in many cases, from a question of an object parametrical structure determination.
Identification problem definition. Let us consider the following modeling scheme of one-dimensional nonlinear dynamic process (fig. 1).
In fig. 1 the designations are accepted: x ( t ) – an output process variable, u ( t ) – the control action, x s ( t ) – an object model output; ( t ) – the continuous time; the index t – discrete time; ht u , ht x – random noise of measurements of process corresponding variables; the index h at object variables for the simplicity reason is omitted: u t = u h , x t = x h ; £ ( t ) - vector random noise.
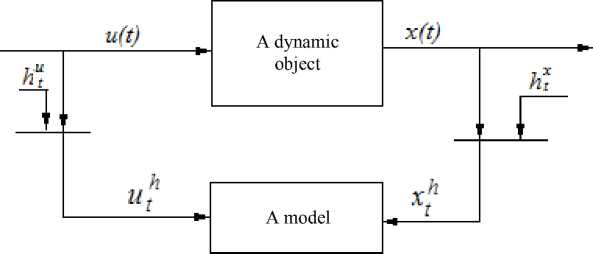
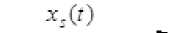
Fig. 1. A flowchart of quasilinear dynamic processes modeling
Рис. 1. Блок-схема моделирования квазилинейных динамических процессов
Let us enter the following designations:
zt = ( z 1 , " ", zk + 1 ) = ( xt - 1 , " ", xt - k , ut ) , (1)
then
x t = f ( z t ) . (2)
Nonparametric identification . As we said before, under conditions of nonparametric indeterminacy the description of an object to within parameters is unknown. In this case, a conditional mathematical expectation of a form can be accepted as an object model:
xs ( t ) = M { x ( t )/ u ( t )}. (4)
In the conditions of nonparametric indeterminacy the structure of nonlinear dynamic process model can be described by the equation in a discrete form:
x t = f ( x t - 1 , x t - 2 , -, x t - k , ut ), (3)
As the studied object model the following nonparametric estimation of regression function on observations { x, , u , , i = 1, 5 } in a discrete form can be accepted [8]:
where f (.) is an unknown functional, k – “the depth” of a dynamic object memory (on A. A. Feldbaum’s terminology) [7]. If we draw analogy to the studied process description in the continuous time in the form of differential equations, then k – an order of the senior derivative in the corresponding equation. It is essential here that the functional type is not defined to within parameters. With regard to redesignations the process model (3) can be shown on the following scheme (fig. 2) which illustrates the dynamic system model in a discrete time reduced to a static system model when not only variables ut , but also xt - 1, xt - 2, ..., xt - k and others are delivered to an entry of the last.
The considered process refers to a class of discrete-continuous, that is the process is continuous by nature, however, the process “input-output” variables are controlled through discrete time points A t , forming an “inputoutput” variables { x , , u , , i = 1, 5 } sample of observations, where s – is a sample size, the index h at object variables for the simplicity reason is omitted.
xs
where
x 1 cs
1 X I u
= -Z x , 'H
5 , = 1 I
^^^^^^B
u cs
- IП — H Ji = 1 c x
( x,
^^^^^^B
x cs
x , - j
,
H ( • ) - a nuclear bell-shaped function, а
u cs ,
k
.., csx – nuclear function blur coefficients which
satisfy convergence conditions [8].
The only output variables x5 - 1 , ..., x5 - k are included in the model (5), which were defined with the use of dynamic process memory depth rule determination [9; 10]. The essence of this rule is as follows: if we put into corre- 12 spondence a nuclear function blur coefficient сsx , сsx , k
..., с 5 for each output variable x5 - 1 ,..., x5 - k of nonparametric estimation (5), which delays at some values, at which the difference between the obtained model and the actual object output will be minimum, then that variable with the smallest coefficient contributes a lot to generation of total estimation and thereby has a greater influence on an output variable. These particular variables have to be considered in model (5). It should be noted that the model (5) can be used only at equal intervals of measurement A t .
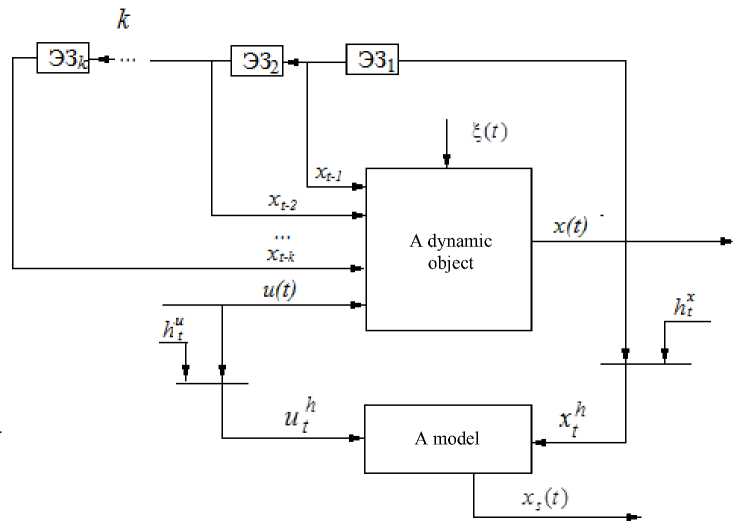
Fig. 2. A quasilinear dynamic process control flowchart
Рис. 2. Блок-схема управления квазилинейным динамическим процессом
Dual control algorithms . Dual control was opened by A. A. Feldbaum in 1960 and developed on the basis of the statistical decisions theory [7]. It should be noted that the studying control systems are systems “with memory”, that means they are not only able to study characteristics of an object, but also, keeping them in memory, to develop rational control actions. The theory of dual management gained its further development in researches of various authors [11–14], in particular B. Vittenmarka [15]. Let us note that when we set a problem, most often the noise probability distribution and also an object parametrical model are assumed to be known. That is the developed regulation algorithms are applicable in conditions when the model structure of an object or a regulator is set to within parameters. In case when the dynamic process structure is not certain, one of possible solutions of a control task is the application of nonparametric adaptive control systems keeping dualism components.
Let us consider an idealized case at first. We enter an object operator A, which describes the process, that is x ( t ) = A < u ( t ) > , where u ( t ) - a control action, x ( t ) – an object output. If there is an operator, inverse to A , that is А - 1, А - 1 А = 1 - a unity operator, then
А - 1 x ( t ) = А - 1 A < u ( t ) > , u ( t ) = A - 1 x ( t ). (6)
Assuming now x ( t ) = x *( t ), where x *( t ) – the setting trajectory, we find from (6) the ideal value u ( t ) = u *( t ). Thus, the type of the ideal regulator ( -regulator) [6] can be presented in the form (6). The main problem is that in most cases operators A and A –1 are unknown, and, therefore, the given method of the -regulator construction becomes very problematic. Therefore, there is a question of dual control scheme construction which is close to actual.
Under conditions of nonparametric indeterminacy the description of an object to within parameters, as it was already mentioned, is unknown. In this case, as direct operator А estimation the conditional expectation (4) can be accepted, and estimates of the inverse operator А– 1:
u * ( t ) = M { u ( t )/ x ( t ) = x * ( t )}. (7)
It is equivalent to “inclusion” of an “anti-object” to the entry of the operated object
If we accept expression (5) as a direct operator А estimation, then the inverse operator А –1 estimation will be (8):
, , < * к k II
u * = 1 £ ur H I x | П 4 H -j-i^ . (8)
s i = 1 I C s ) j = 1 c S I c S J
The nonparametric dual control algorithm explicitly described in [6] is:
the operating action us + 1, the first augend, that is u * starts obtaining an escalating role. Thus, in the process of an object dual control both the stage of object studying, and the stage of its reduction to the purpose appear.
For control estimation the relative error was used:
W = R s I D s , (10)
1 s 2
where Rs = - ^( x i - x * ) , x i - an output variable meas- s , =1 v '
ured value, xi * – the setting action, D s – estimation of the output variable x t dispersion.
Computing experiment . Let us consider the linear case for a start. Let an object be described by the following simple equation:
xt = 0.2 • xt - 1 - 0.3 • xt _ 2 + 0.4 • xt _ 3 + 1.5 ut . (11)
In the described experiment the training sample is formed in the following way. Let a series of various input actions u 1( t ) - u 4( t ) be described by the equations (12), their charts are in fig. 3.
u 1( t ) = 0.6 + 0.3 • sin (0.15 • t );
u 2( t ) = 0.5 + 0.2 • cos(0.05 • t );
u 3( t ) = 0.23 + 0.1 • sin (0.2 • t ); (12)
u 4( t ) = 0.1 + 0.4 • sin (0.2 • t );
u 5( t ) = 0.3 + 0.8 • sin (0.05 • t ).
The received values form the common input variables u ( t ) sample defined in the range of u ( t ) e [ - 0.5,1.1]. The values of the input variable u ( t ) are substituted in the equation ( 12 ), thus we receive an input-output variables { xi , ui , i =1, s } sample, where s – the training sample size. In this case s = 500.
For the offered identification algorithm operability check we will create a new sample of input actions u 6( t ) = 1 + 0.5 • sin (0.1 • t ). The identification algorithm is carried out according to the following scheme. We set initial value k = 6. Further we develop a model in pursuance of formula (5). The relative modeling error is W 0 = 0.017. Further we find optimum coefficients with the coordinate descent algorithm use. The found coefficients are equal to с 4 = 0.38 - at u t , с * = 0.231 - at xt - 1, с 2 = 0.378 - at xt - 2, с * = 0.456 - at xt - 3, с * = 1.876 -at xt - 4 , с * = 1.999 - at xt - 5, с * = 1.983 - at xt - 6. After realization of all algorithm stages, variables xt - 4 , x t - 5, x t - 6 were excluded. Thus the developed dynamic object final structure is:
*
u s + 1 = u s + A u s + 1
xs = « 1 xt - 1 + « 2 xt - 2 + « 3 xt - 3 + P ut,
where us * – an augend in charge of an object information accumulation, and A us + 1 = e ( x * + 1 - xs ) - the “studying” search steps. Let us analyze the character of algorithm dualism (9). On the initial control step the main role belongs to the second addend A us + 1 from formula (9). It is a case of active information accumulation in the system of dual control which begins with the first observation of input and output object variables emergence. In the process of training (information accumulation) when forming
what corresponds to a difference object equation structure (11), and a nonparametric model is:
xs
x 2 сs
I
x s - 2 x i - 2
x
s
• 4 Ф x сs
x 3 сs
x s - 1 - x - 1
x cs
r_.
x s - 3 x i - 3
к
x cs
к
x
The forecast of the output x 6 ( t ) variable with nonparametric model use (13) is shown in fig. 4.
The relative identification error for the first experiment is equal to W = 0.12, that means satisfactory quality of the model. Thus, it is possible to draw a conclusion that the nonparametric algorithm (5) can be applicable for the linear dynamic processes identification with the known depth of memory k . We enter power functions into the process input difference equation. Let the object equation be described as:
x t = 0.2 • x t 1 - ! - 0.3 • x t _ 2 + 0.4 • x 1 - 2 3 + 1.5 ut . (14)
Let the process (14) be affected by the additive noise level ^ ( t ) = 5 %, distributed according to the normal law with a zero expectation and dispersions 1. To model a random value distributed according to the normal law the method of polar coordinates was used. The coefficient of k was found in the same way as earlier. The results of object identification (14) when delivering to the entry of input action u 6( t ) are shown in fig. 5.
The relative identification error for the second experiment is equal to W = 0.19, that also means satisfactory model quality, even at rather high level of the external noise affecting the process. From the analysis of fig. 5 and relative error values, it is possible to draw a conclusion that in spite of the fact that the process (14) does not refer to the linear processes class, the nonparametric algorithm (5) copes with an identification task, and, thus, it can be applicable also for identification of nonlinear dynamic processes at partial nonparametric indeterminacy.
Let us consider the possibility of nonparametric algorithms application to control different types of quasilinear dynamic objects. To begin with, in the first experiment we will consider the linear dynamic object which is described by the following simple equation:
xt = 0.2 • xt , - 0.3 • xt - 2 + 0.4 • xt - 3 + 1.5 ut . (15)
The results of nonparametric object control (15) with the use of control law (9) are presented in fig. 6. In fig. 6 the case of active information accumulation is presented, that is the initial training sample before performing an experiment was absent.
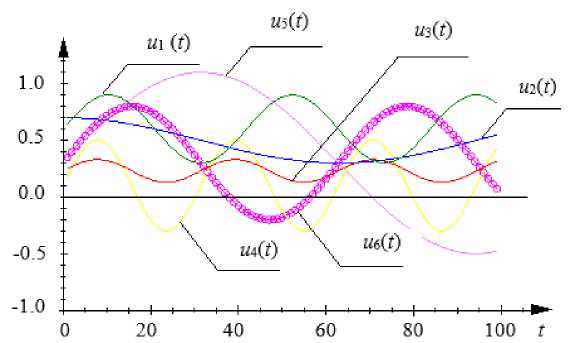
Fig. 3. Series of input actions u 1 ( t ) - u 4 ( t )
Рис. 3. Серия входных воздействий u 1 ( t ) - u 4 ( t )
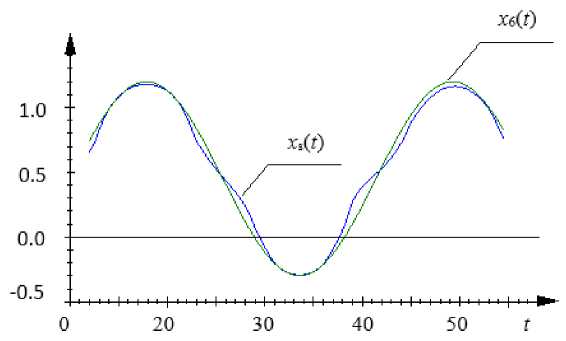
Fig. 4. Object output (11) x 6 ( t ) and nonparametric model output (13) xs ( t ), at an input variable u 6 ( t ) delivered to the entry
Рис. 4. Выход объекта (11) x 6( t ) и выход непараметрической модели (13) xs ( t ) при подаче на вход входной переменной u 6 ( t )
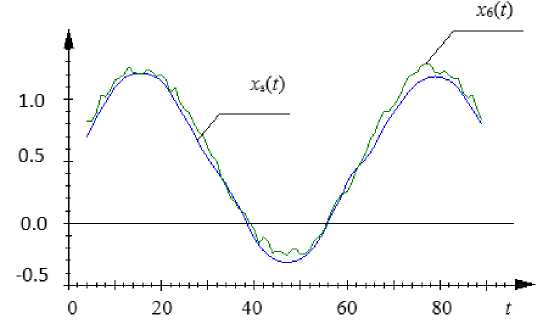
Fig. 5. Object output (14) and nonparametric model output x 6 ( t ) (14) xs ( t ), when delivering an input variable u 6( t ) to the entry, with the noise £ ( t ) = 5 %
Рис. 5. Выход объекта (14) x 6( t ) и выход непараметрической модели (14) xs ( t ) при подаче на вход входной переменной u 6( t ), при помехе £ ( t ) = 5 %
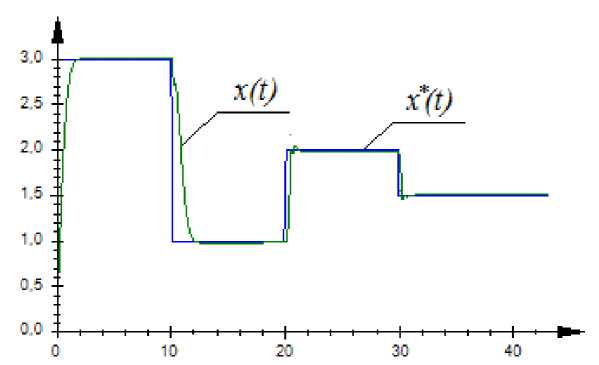
Fig. 6. Linear dynamic object control (15)
Рис. 6. Управление линейным динамическим объектом (15)
The relative control error for the first experiment is equal to W = 0,076, this suggests high quality of nonparametric control. In the analysis of figure 6 it is possible to observe how the dual control algorithm at active information accumulation behaves. On the initial steps of control, from the 1st to the 20th steps, the algorithm needs more time for reduction of an object to the control action as at this stage a sample training and accumulation take place. After the training level, starting from the 20th step, at the control action change an output object variable practically at once becomes equal to the task. We consider the possibility of nonparametric control algorithm application (9) for quasilinear dynamic systems. In the following experiments dynamic objects with different degree of nonlinearity will perform as the studied objects.
Let the dynamic object difference equation contain power functions, the object equation is described as follows:
xt = 0,2 ■ Х 1 - 2 - 0,3 ■ x t _ 2 + 0,4 ■ x t - 3 + 1.5 ut . (16)
The results of object control (16) at passive information accumulation, that is in case when there is a training sample with the size equal to s = 300, are presented in fig. 7.
The relative object control error (16) is equal to W = 0,085. We increase a sample size to s = 500 (fig. 8).
For the experiment presented in fig. 8 the relative control object error (16) is W = 0.045. We enter a ^ = 5 % noise level (the noise is added to an output variable measurement, distributed by normal distribution), the control results for this experiment are presented in fig. 9.
Thus, from the analysis of fig. 7–9 and values of the relative control errors, it is possible to draw a conclusion that the nonparametric control algorithm (9) successfully copes with the task of quasilinear dynamic systems regulation in case of passive information accumulation, even at external noise influence on the object under study, at the same time the quality of control practically does not differ from the linear object control at active information accumulation.
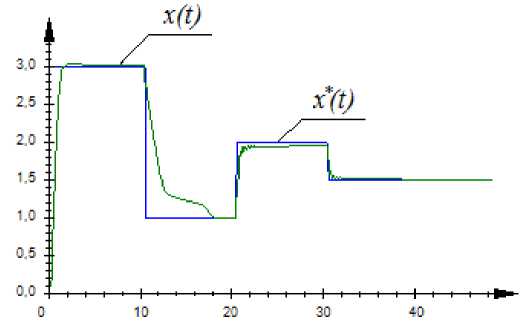
Fig. 7. Dynamic object control (16) at a sample size s = 300
Рис. 7. Управление динамическим объектом (16) при объеме выборки s = 300
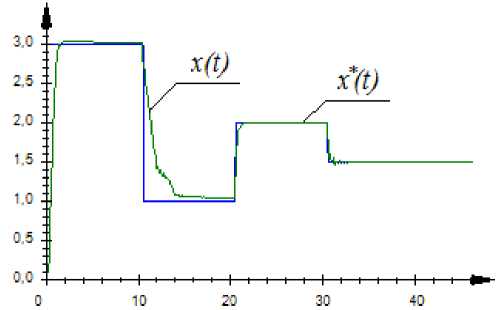
Fig. 8. Quasilinear dynamic object control (16) at a sample size s = 500
Рис. 8. Управление квазилинейным динамическим объектом (16) при объеме выборки s = 500
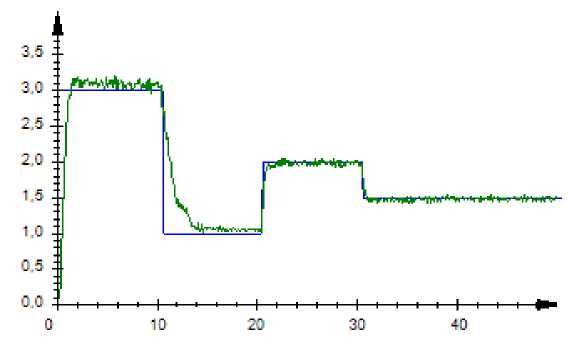
Fig. 9. Quasilinear dynamic object control (16) at a sample size s = 300, £ = 5 % noise level
Рис. 9. Управление квазилинейным динамическим объектом (16) при объеме выборки s = 300, помеха £ = 5 %
We consider the dependence of the relative control error W on a power function index p (fig. 10). A variable function index will change x t _ 3: x t = 0.2 ■ x t - 1 - 0.3 ■ x t _ 2 + + 0.4 ■ xp з + 1.5 u, . t — 3 t
Fig. 10 shows that if a power function index is less than 1.5, a relative control error is sufficiently low. On the contrary, at power function index increase more than 1.6, the sharp increase of the relative control error is observed. Information on dependence of the relative modeling error on the studied function type is provided in table.
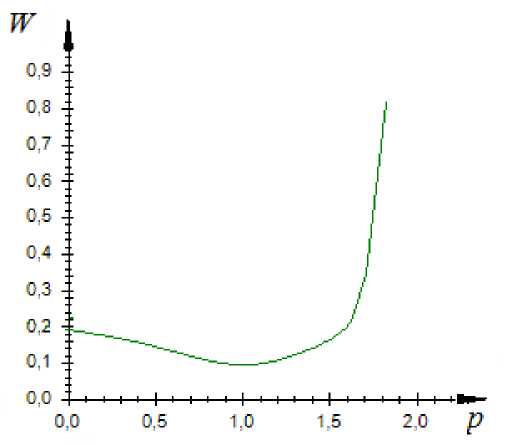
Fig. 10. Dependence between the relative regulation error on a power function index
Рис. 10. Зависимость между относительной ошибкой регулирования и показателем степенной функции
Dependence of the relative control error on an object equation type
|
Type of the equation |
The relative control error |
|
I. The linear equation: x t = 0.2 • x t - 1 - 0.3 • x t _ 2 + 0.4 • x t _ 3 + 1.5 ut |
0.076 |
|
II. Non-linear equations (algebraic) xt = 0.2 • x ^^ - 0.3 • x t _ 2 + 0.4 • x t _ 3 + 1.5 ut |
0.085 |
|
xt = 0.2 • x t - 1 - 0.3 • x^ + 0.4 • xt _ 3 + 1.5 ut |
0.088 |
|
xt = 0.2 • xt - 1 - 0.3 • xt _ 2 + 0.4 • x^ + 1.5 ut |
0.113 |
|
xt = 0.2 • x t 1^ - 0.3 • x ^ + 0.4 • x^ + 1.5 u t |
0.124 |
|
x t = 0.2 • x t 5 - 0.3 • x t - 2 + 0.4 • x t - 3 + 1.5 u t |
0.115 |
|
x t = 0.2 • xt 2 - 1 - 0.3 • xt - 2 + 0.4 • xt - 3 + 1.5 ut |
0.66 |
|
xt = 0.2 • xt - 1 - 0.3 • x t 2 - 2 + 0.4 • xt - 3 + 1.5 ut |
0.78 |
|
xt = 0.2 • xt - 1 - 0.3 • xt - 2 + 0.4 • д/ xt - 3 + 1.5 ut |
0.082 |
|
xt = 0.2 • xt - 11.5 - 0.3 • -Jxi- 2 + 0.4 • xt - 3 + 1.5 ut |
0.23 |
|
xt = 0.2 • —-- 0.3 • xt - 2 + 0.4 • xt - 3 + 1.5 ut x t - 1 |
0.456 |
|
III. Non-linear equations (transcendental) xt = 0.2 • sin ( xt - 1 ) - 0.3 • xt - 2 + 0.4 • xt - 3 + 1.5 ut |
0.105 |
|
xt = 0.2 • xt - 1 - 0.3 • log 10 ( xt - 2 ) + 0.4 • xt - 3 + 1.5 ut |
0.128 |
|
xt = 0.2 • e x - - 0.3 • xt - 2 + 0.4 • xt - 3 + 1.5 ut |
0.89 |
|
xt = 0.2 • cos( xt - 1 ) - 0.3 • xt - 2 + 0.4 • sin( xt - 3 ) + 1.5 ut |
0.117 |
From the table analysis it is possible to draw the following conclusions: if the dynamic object difference equation contains degrees up to the second order, the control algorithm (9) successfully copes with the control task.
The relative control error increases if the power function is entered for the variable at which the coefficient has a greater influence on an output value. At increase in degree the quality of control considerably worsens. If the degree at some variable is equal to 2 or more in a difference equation, then a nonlinear dynamic object control with a control algorithm (9) use is impossible.
If an object difference equation contains fractional degrees, the control algorithm (9) also copes with the control task. The results of this computing experiment show that even at each variable involution, the control algorithm (9) copes with the task of an object reduction to the setting action. It is also possible to notice that if a dynamic object difference equation contains trigonometric or logarithmic functions, then a control algorithm application (9) is possible. The considerable deterioration of control is observed in the presence of exponential function in the object equation. At the negative degrees the control quality considerably decreases.
Conclusion. The following important conclusion can be considered as the result of the present article. Nonparametric algorithms, as it was previously known, can be efficiently applicable for identification problem solving and also are rather qualitatively able to conduct the operated process of the linear class or category. It was naturally interesting, what if the process is nonlinear, in a varying degree. The computing experiments given above showed that identification and control algorithms can be also used for nonlinear dynamic objects control or objects for which the principle of superposition is not performed any more. Thus, the main conclusion which we can make is that the class of dynamic discrete continuous processes slightly extends for the nonparametric identification and control theory of the linear dynamic processes.
Список литературы On nonparametric identification and dual control of quasilinear dynamic processes
- Павленко В. Д. Идентификация нелинейных динамических систем в виде ядер Вольтерра на основе данных измерений импульсных откликов//Электронное моделирование. 2010. Т. 32, № 3. С. 3-18.
- Гельднер K., Кубик С. Нелинейные системы управления: пер. с нем. М.: Мир, 1987. 368 с.
- Андриевский Б. Р., Матвеев А. С., Фрадков А. Л. Управление и оценивание при информационных ограничениях: к единой теории управления, вычислений и связи//Автоматика и телемеханика. 2010. № 4. С. 34-99.
- Коплярова Н. В., Медведев А. В. Непараметрические алгоритмы управления системами класса Гаммерштейна//Вестник СибГАУ. 2015. Т. 16, № 1. С. 62-73.
- Коплярова Н. В. О непараметрической идентификации стохастических объектов класса Винера//Системы автоматизации в образовании, науке и производстве: Тр. IX Всерос. науч.-практ. конф./под ред. С. М. Кулакова, Л. П. Мышляева; Сиб. гос. индустр. ун-т. Новокузнецк: Изд. центр СибГИУ, 2013. С. 445-451.
- Медведев А. В. Основы теории адаптивных систем/СибГАУ. Красноярск. 2015. 525 c.
- Фельдбаум А. А. Основы теории оптимальных автоматических систем. М.: Физматгиз, 1963. 552 с.
- Надарая Э. А. Непараметрические оценки плотности вероятности и кривой регрессии. Тбилиси: Изд. Тбил. ун-та, 1983. 194 с.
- Раскина А. В. Определение структуры линейного динамического объекта в задачах непараметрической идентификации//Вестник СибГАУ. 2016. Т. 17, № 4. С. 891-898.
- Медведев А. В. Адаптация и обучение в условиях непараметрической неопределенности//Фундаментальные исследования (физико-математические и технические науки). Новосибирск: Наука. Сиб. отд-ние, 1977. С. 92-97.
- Wenk C. J., Bar-Shalom Y. A multiple model adaptive dual control algorithm for stochastic systems with unknown parameters//Automatic Control: IEEE Transactions on. 2003. Vol. 25, iss. 4. Pp. 703-710.
- Duan Lia, Fucai Qianb, Peilin Fuc. Optimal nominal dual control for discrete-time linear-quadratic Gaussian problems with unknown parameters//Automatica. 2008. Vol. 44, iss. 1. Pp. 119-127
- Tse E., Bar-Shalom Y. An actively adaptive control for linear systems with random parameters via the dual control approach//Automatic Control: IEEE Trans-actions on. 2003. Vol. 18, iss. 2. Pp. 109-117.
- Filatov N. M., Keuchel U., Unbehauen H. Dual control for an unstable mechanical plant//Control Systems: IEEE. 1996, Vol. 16, iss. 4. P. 31-37.
- Wittenmark B. Adaptive dual control methods: An overview//5th IFAC Symposium on Adaptive Systems in Control and Signal Processing. 1995. Pp. 67-72.


