On one equation of internal waves
Бесплатный доступ
The Cauchy-Dirichlet problem is considered for the equation of internal waves. This equation has various applications in hydrodynamics, for example, in the study of waves in the ocean. The article provides an analytical study of one equation of internal waves. This equation characterizes propagation of waves in a homogeneous incompressible stratified fluid. The equation of internal waves is reduced to an abstract semilinear Sobolev type equation of the second order. The study of the equation is carried out within the framework of the theory of polynomially bounded operator pencils. In this work, we construct propagators for the equation of internal waves. Also, we present two model examples, where the domain D is represented in the form of a cylinder and a parallelepiped. The result of the work is an analytical solution to the considered cases for the equation of internal waves.
Internal wave equation, polynomially bounded pencils of operators, sobolev-type equation, propagators
Короткий адрес: https://sciup.org/147232860
IDR: 147232860 | DOI: 10.14529/mmph210202
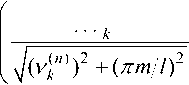
Список литературы On one equation of internal waves
- Габов, С.А. О малых колебаниях отрезка, помещенного на границу раздела двух стратифицированных жидкостей / Габов С.А., Крутицкий П.А. // Ж. вычисл. матем. и матем. физ. - 1989. - Т. 29, № 4. - С. 554-564.
- Плетнер, Ю.Д. Фундаментальное решение уравнения внутренних волн и некоторые начально-краевые задачи / Ю.Д. Плетнер // Ж. вычисл. матем. и матем. физ. - 1991. - Т. 31, № 4. - С. 592-604.
- Перова, Л.В. О распространении возмущений, возбуждаемых в жидкостях движущимися источниками / Л.В. Перова, А.Г. Свешников // Ж. вычисл. матем. и матем. физ. - 2010. - Т. 50, № 12. - С. 2223-2232.
- Соболев, С.Л. Об одной новой задаче математической физики / С.Л. Соболев // Изв. АН СССР. Сер матем. - 1954. - Т. 18, № 1. - С. 3-50.
- Васильев, В.В. Полугруппы операторов, косинус оператор-функции и линейные дифференциальные уравнения / В.В. Васильев, С.Г. Крейн, С.И. Пискарев // Итоги науки и техн. Сер. Мат. анал., ВИНИТИ - 1990. - Вып. 28. - C. 87-202.
- Свиридюк, Г.А. Линейные уравнения соболевского типа / Г.А. Свиридюк, В.Е. Федоров. - Челябинск, 2003. - 179 с.
- Демиденко Г.В. Уравнения и системы, не разрешенные относительно старшей производной / Г.В. Демиденко, С.В. Успенский. - Новосибирск: Научная книга, 1998. - 436 с.
- Замышляева, А.А. Фазовое пространство уравнения соболевского типа высокого порядка / А.А. Замышляева // Известия Иркутского государственного университета. - 2011. - Т. 4, № 4. - С. 45-57.
- Zamyshlyaeva, A.A. The Cauchy Problem for the Sobolev Type Equation of Higher Order / A.A. Zamyshlyaeva, E.V. Bychkov // Вестник ЮУрГУ. Серия "Математическое моделирование и программирование". - 2018. - Т. 11, №. 1. - С. 5-14.
- Свиридюк, Г.А. Фазовые пространства одного класса линейных уравнений соболевского типа высокого порядка / Г.А. Свиридюк, А.А. Замышляева // Дифференц. уравн. - 2006. - Т. 42, № 2. - С. 252-260.
