On one solution of the numerical problem differentiation in calculation vertical speed of aircraft

Statement of the problem

One of functions of the system of air signals (ASS) is the problem of calculation of vertical velocity of the aircraft. As a rule, this problem is solved by method of numerical differentiation of signal of the barometric height determined by ASS. The algorithm of calculation of vertical velocity as it is well known [1], can be written down as follows:

h = h ₀ + ^{T 0}{1 - ( ^p ) ↑ ( γ ^R )} ⇒ ^{dh (} τ ⁾ =- ^{RT 0} × ( ^p ) ↑ ( γ ^R - 1) ∂ ^p ,                          (1)

γ     p0    g      dτ     g p0   p0     g ∂τ where γ = 0.0065 K/м – temperature gradient, g – acceleration of gravity, R – gas constant, p (τ) – atmospheric pressure on the altitude h (τ) , τ – time, p0 and T0 – respectively pressure and temperature at some height h0 , taken for the beginning of its counting, ↑ – operation of exponentiation.

It is clear that both atmospheric pressure and relative altitude are determined with errors. Because of this, as is well known, the problem of a sufficiently accurate numerical estimate of the signal derivative with errors is difficult to implement, primarily due to its incorrectness [2–5]. Algorithms known in the literature [2–14] are based on different ideas and approaches, these algorithms have been developed for specific problems and conditions, and are characterized by different advantages and disadvantages. Therefore, directly, without additional tuning and optimization, it is rather difficult to use one or another well-known algorithm; there is an urgent need to develop a specific method for implementing the differentiation procedure for a specific problem to be solved.

So-called dot algorithms are known, for example, the simplest point-to-point algorithm of differentiation used, in particular, and in SVS is represented by means of the following formula [6–8, 15]:

dx ( τ _{i + 1}) ≈ x_{i + 1} - x_i d τ      Δτ

where x ( τ ) – the measured signal, Δτ – period between the information retrieval moments

Ат = т i + 1 -Т i , i = 0,1,2,... , т i = i хАт .

It is known also that the best accuracy is reached when using point-to-point algorithm of the central approximation [6]. However the big accuracy of calculation of derivative can be reached when using multipoint algorithms, in particular, due to averaging of results of calculations of derivative for two next points on point-to-point algorithm with step 2 Δτ [9, 15].

In addition, various regularizing algorithms are also known [2–14]. It often uses algorithms based on the approximation of the measured signal by an algebraic polynomial followed by its analytical differentiation [7, 9–11], for example, in [11], cubic spline approximation of the measured data is used.

It is necessary to notice that regularization as a matter of fact as it is frequent and is specified in literature, represents suppression (filtration) of high-frequency component of measurement error of signal. As it is represented to us, and some multipoint algorithms including procedures of averaging in the structure can also be carried to regularizing algorithms.

In [13], to solve the differentiation problem, a frequency approach is used, an approximating function with a finite frequency spectrum is selected according to the properties of its derivative, here regularization is reduced to minimizing the Euclidean norm of the derivative estimate.

The problem of differentiation can be solved and as follows. It is well known that ^τ dx ( τ )

dτ = x(τ) - x(0) . If at the same time x(0) =0 (in this case there is no need to tie the decision to 0 dτ different entry conditions – values x(0) ) i. e. if the task is brought to zero entry conditions that it is simple to implement, then the problem of differentiation comes down to the solution of the integrated τ dx(τ)                        dx(τ)

equation         d τ = x ( τ ) relatively . Such regularizing approach is used in work [12].

₀ d τ                        d τ

According to the data of [9, 15], both point and approximating approaches are used in the ASS, in particular, in the SVS-2Ts-1M, a two-point algorithm (2) [9] is implemented, piecewise-polynomial approximation of all dependences used to calculate the altitude and speed parameters of the aircraft. In this d h ( τ )

case, naturally, it is not difficult to find an analytical expression for the derivative          and deter- dτ mine its numerical value.

In [8] estimates of derivative are calculated on the simplest point-to-point algorithm (2) with the same period of time between points . At the same time it is considered that on the interval of time used at calculations the true derivative is equal to the same value, i. e. is const . For search of the resulting asses-

Панферов В.И., Панферов С.В.,        Об одном решении задачи численного дифференцирования

Хаютин А.М., Тренин Н.А.            при вычислении вертикальной скорости воздушного судна sment of derivative the system of the linear algebraic equations (SLAE) is solved. It is established what with increase in quantity of private estimates based on the ratio of (2) accuracy of the resulting assessment of derivative increases, however increases also computing complexity of the procedure that can serve as obstacle for its use in real time.

The algorithm of work [12], based on the solution of an integral equation, is also computationally complex. Similar in complexity to the algorithms of [8] and [12] should be considered the algorithms of [11, 13], which also require the solution of the SLAE.

In [14], it is noted that often when differentiating signals, the speed of the methods and the possibility of their use in real time are in demand, all this, of course, is determined by their computational resource intensity. It is indicated that the regularizing algorithm of A.N. Tikhonov, in which the integral equation is solved, requires large computational resources.

Also the calculators of vertical velocity using methods of hardware differentiation (the differentiating amplifiers are used) are known [16, 17]. However such measuring instruments as it is known, on number of indicators it is much worse than digital differentiators.

Thus, the problem of numerical differentiation is still far from its final solution; it is required to develop sufficiently reliable and computationally simple algorithms that sufficiently meet the requirements imposed on them. Moreover, when applying any approach, preliminary filtering of the differentiated signal can be applied.

Algorithm for calculating the derivative

Let's consider the following solution of objective. First, we will evaluate signal mean in ( i + 1) -ty timepoint on four points including the current measurement and three previous i. e.

x = ⁽ xi + 1 ⁺ xi ⁺ xi - 1 + xi - 2 ) / 4.                                                                             ⁽³⁾

It is known that the arithmetic average is more exact assessment of true value, than result of one measurement.

Secondly, let us refer the average value found in this way to x the middle of the time interval on which these points are located. The location of the points used is shown in Fig. 1.

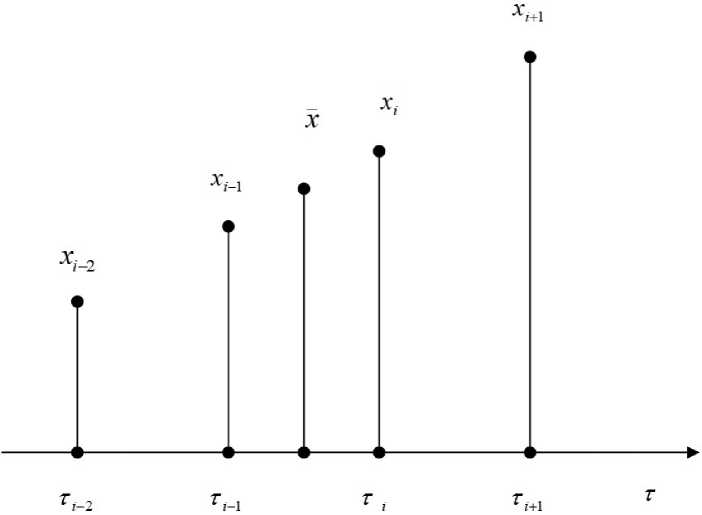
Fig. 1. The layout of the points used for differentiation

It is obvious that in this case it is possible to use the following four estimates of derivative of signal in ( i + 1)-ty timepoint:

dx ( τ _{i + 1}) ≈ x_{i + 1} - x ;

dτ     1.5Δτ dx(τi +1) xi - x dτ 0.5Δτ ;

dx ( τ _{i + 1}) x - x_{i - 1} d τ 0.5 Δτ ;

dx ( τ _{i + 1}) ≈ x - x_{i - 2} .                                                                                         (7)

d τ       1.5 Δτ .

It is well-known that the best assessment of derivative in ( i + 1) -ty timepoint will be arithmetic average of the found private estimates for this purpose ( i + 1) -th timepoint, i. e.

i + 1 ) [ x i + 1 - x + x i - x + x - x i - 1 + x - x i - 2 ]/4 1.5 Δτ    0.5 Δτ    0.5 Δτ     1.5 Δτ

=    [ ( x_{i + 1} - x ) + 2( x_i - x ) + 2( x - x_{i - 1}) + ( x - x_{i - 2})]/4 =

Δτ 33

11         11

x_{i - 1}) + ¹( x - x_{i - 2})] = 6

=     [ ( x_{i + 1} - x ) + ( x_i - x ) + ( x -

Δτ 6          22

= ¹ [( x_{i + 1} - x ) + 3( x_i - x ) + 3( x - x_{i - 1}) + ( x - x_{i - 2})] = 6 Δτ

= ¹ [ x_{i + 1} + 3 x_i - 3 x_{i - 1} - x_{i - 2}].

6Δτ

As it is visible from formula (8), bigger weight is given to values of signal in i -ty and ( i - 1) -th timepoints, and three times smaller weight to its values, extreme for the considered period, that is rather expedient.

It should be noted that due to the averaging of both the measurement results themselves (the arithmetic mean of the readings is used) and the estimates of the derivatives, noise filtering will be carried out, this is a well-known and absolutely verified result. In addition, as can be seen from formula (8), the algorithm is quite simple computationally, which, of course, is its undoubted advantage.

Computing research of algorithm of differentiation

Fig. 2 shows the curve of the change in the height of the aircraft (AC) during the flight, while in the process of modeling for a regular (useful) signal of the form h ( τ ) = h (0) + 3.5 ×τ+ a × sin( ωτ ) , where h (0) – height of the beginning of maneuver of VS, interference was superimposed – the noise component of the barometric altitude signal. The interference was simulated using a random number generator with a uniform distribution law.

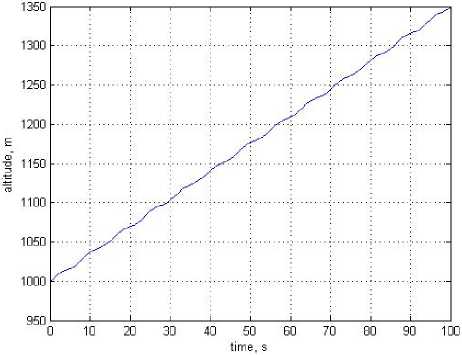
Fig. 2. Aircraft altitude change curve during flight

Fig. 3 shows the graphs of changes in the estimate of the derivative of the height – the vertical speed of the aircraft according to the algorithm (2), and in Fig. 4 according to algorithm (8). In this case, naturally, it was assumed that x ( t ) = h ( t ) .

Apparently from Figs. 3 and 4 the availability of sinusoidal component in regular part of signal is rather distinctly monitored by both algorithms. It indicates rather high speed of both algorithms. The accidental component as it is visible from Figs. 3 and 4, affects result of assessment on algorithm (8), than on algorithm (2) much less that confirms significant efficiency of algorithm (8). Therefore as a part of algorithmic providing SVS it is more preferable to use algorithm (8), but not algorithm (2).

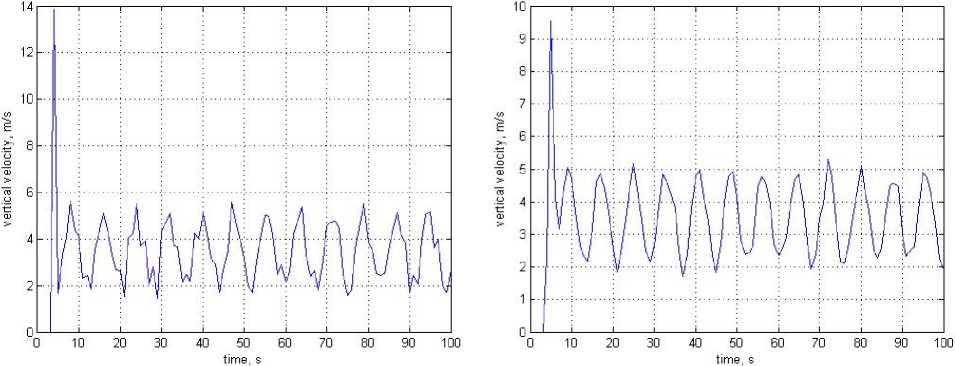
Fig. 4. Results of calculating the vertical speed by the algorithm (8)

Fig. 3. Results of calculating the vertical speed by the algorithm (2)

Joint schedules of change of estimates of derivative on algorithm (2) – continuous and on algorithm (8) – dash-dotted curves when the sinusoidal component, i. e. for case is excluded from regular part of signal of height are provided on Fig. 5 h ( t ) = h (0) + 3.5 xt and in this case the noticeable efficiency of algorithm is visible (8).

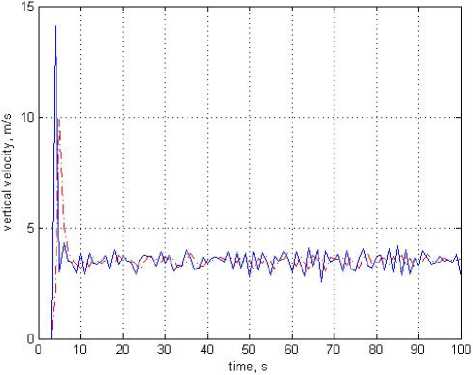
Fig. 5. Changing Derivative Estimates

In all cases the big errors of assessment at the beginning of curves are explained by availability of transitional component in work of algorithms.

Preliminary filtration of signal of height

As is well-known [2, 3] error of calculation of derivative has two components: 1) computing error – the error caused by rounding and representation of values of signal in the computer; 2) the error con- nected with signal measurement errors (errors of basic data). It is known also that if influence of the second component is not too big and if the useful component of signal not too quickly changes (“…behaves ‘rather well’” [8], then dot algorithms of differentiation yield almost acceptable results. Otherwise it is necessary to use special approaches to the solution of problem, in particular, of the procedure of preliminary smoothing [18], recommend to use also algorithms of preliminary filtration of signal of height. In this regard we will consider question of creation of such algorithm.

We will consider problem of preliminary filtration as the following problem of optimization [19]:

V 1 ( h i ^{- h ф)2} + V 2 ^{( hф -} h i - 1 )² ^ min,                                                         ⁽⁹⁾

hiФ where hi – measured signal value in i -ty moment (counting), hiФ – evaluation of the useful signal for i -th point in time (filter output), V1 and V2 — weight coefficients.

Solving this problem of optimization, have established that optimum assessment of useful signal has to be determined by the following formula:

h ф = V 1 ^hi +V 2 А Ф1

i     V 1 +V 2

At such value hiФ the minimum of criterion (9) as the second derivative calculated in this point is equal is really reached 2 V1 + 2 V2 > 0 •

Sometimes for realization to write down conveniently this ratio in the following look:

h ф = h ® +-^V^ ( h i - h i - , ).                                                       (11)

V 1 +V 2

Apparently from the last equation if the signal has not changed for period between ( i - 1) -th and i -m the moments, then estimates h_/ ^Ф and h i - 1 will coincide. Besides, we will note that reduction V 1 and increase v ₂ leads to strengthening of the filtering properties of algorithm. It is explained by the fact that the component v ₂( h ^ф — h i - 1 )² of criterion (9) sets proximity of the next estimates.

It is generally recommended concrete values V i and v ₂ to select, proceeding from real statistical situation on subject to control. To the place we will notice that this algorithm of filtration is quite successfully approved in works [20–22].

Let's note also that the algorithm (11) can be presented also in the following form:

^hi ^Ф

—^— h + (1 — ^_ ) h i » =

V 1 +V 2        V 1 +V 2

K =  V1

V 1 +V 2

= Kh i + (1 - K ) h £_P

It representations is most characteristic of the algorithms of filtration developed with use of approach of Kallman [18, 23], only in this case the optimum value of coefficient of Kallman K is found from the solution of the following problem of optimization:

M { e i ²} = M {( h_z ^H - h Ф )²} ^ min, (13)

i. e. the expected value of square of mistake – the difference between the output of the filter and true value of the measured quantity is minimized h_i ^И . At the same time it should be noted that in task (13) structure of algorithm of filtration – the ratio (12) is set a priori, only the optimum value of coefficient of Kallman is found. Solving problem (9), we, on the contrary, find optimum structure of algorithm of filtration which as it is shown, coincides with that structure which a priori is accepted in Kallman's tasks.

Results of assessment of vertical velocity for conditions of Fig. 1 at additional use of the offered filter (11) are given in Figs. 6 and 7. Setup of the filter coefficient of Kallman in both cases it is equal K = 0.2.

Apparently from Figs. 6 and 7 the filtration significantly increases the accuracy of assessment both on the simplest point-to-point algorithm (2), and on the offered algorithm (8), oscillation frequency in both cases has considerably decreased. Thus, the algorithm (11) has the noticeable filtering properties, on temporary sign it should be carried to algorithm of the late estimation [20–22] that is quite explainable as the algorithm on characteristics is close to inertial link of the first order (exponential smoothing of the first order) [24].

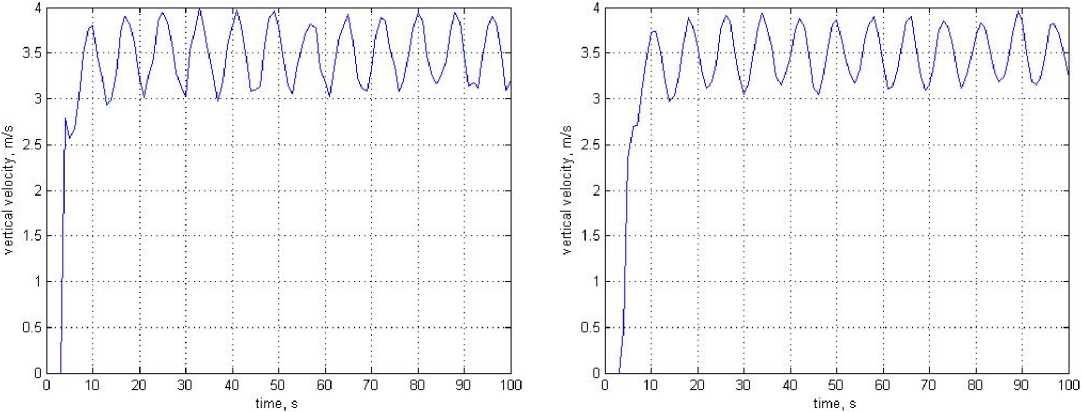
Fig. 6. Estimation of aircraft vertical speed according to algorithm (2) with preliminary filtering of the altitude signal

Fig. 7. Estimation of aircraft vertical speed using algorithm (8) with preliminary filtering of the altitude signal

Indeed, the operation of the algorithm can be represented as follows. Let experimental information h(τ) is fed to the input of the inertial link of the 1st order, and the output value of such a link is the current estimate of the useful signal – the filter output hф(τ) (Fig. 8). Here p – the operator of differentiation.

Then [24] differential equation connecting entrance and output sizes will have appearance:

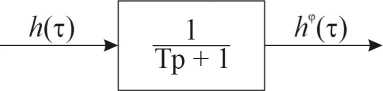
Fig. 8. The signal processing unit

T ^{dhi ф(} τ ⁾ + hi ^ф( τ ) = hi ( τ ). d τ

Here T – constant of time of inertial link. It is known that finite difference approximation of this equation can be written down as follows:

T ^{hi   hi - 1} + h ^ф = h .                                                                                  (15)

Δτ ^{i i}

Further, it is easy to rewrite the equation (15) in the look similar to the equation (11)

hi ^ф = hi ^ф - 1 + Δτ ( hi - hi ^ф - 1 ).                                                                            (16)

T + Δτ

Comparing equations (11) and (16), we can conclude that the parameter ψ ₁ can be interpreted as a discreteness interval Δτ , and the parameter ψ ₂ as a link time constant T . Therefore, it becomes extremely clear that decreasing ψ ₁ and increasing ψ ₂ (time constant) leads to an increase in the filtering properties of the algorithm. The deviation of the estimates obtained from its true values decreases markedly. In our calculations, it was always possible to bring this deviation to an acceptable value due to the filtering algorithm settings (by choosing ψ ₁ and ψ ₂ ). Thus, the use of algorithms (8) and (11) makes it possible to obtain a completely efficient procedure for estimating the aircraft vertical speed.

Conclusions

The algorithm of numerical differentiation differing in small computing complexity and essential bigger accuracy than the point-to-point algorithm used in algorithmic providing SVS is offered and approved. The algorithm is complemented with the procedure of preliminary filtration of signal of barometric height of VS, the algorithm of filtration is the solution of problem of optimization on assessment of useful signal by results of measurements. Results of work are recommended for use when developing algorithmic providing SVS of aircraft.