On Some Results Based on Geometrical Representation of Fuzzy Sets

Published Online June 2013 in MECS

Fuzzy set theory has been initiated by an observation made by Zadeh [1], saying that “more more often than not, the classes of objects encountered in the real physical world donot have precisely defined membership”. That is to say that the theory of fuzzy sets was first introduced by Zadeh as an appropriate mathematical instrument for description of uncertainty observed in nature.

The particularity of fuzzy sets is to capture the idea of partial membership.The characteristic function of fuzzy sets often called membership function, is a function whose range is an ordered membership set containing more than two values (typically the unit interval). Therefore fuzzy set often understood as a function. The complement of a fuzzy set is defined with a membership function which is one minus the membership function of the given set. Since the inception of the theory, it has got intensive acceptability in various fields.

The fuzzy sets and their corresponding membership function provided by the experts may not be suitable for defining the complement of fuzzy sets which can be clear from the following sections.

In this article, our study is concerned with the revision of the geometrical representation of fuzzy sets and some of the properties associated with this. Then these results are interpreted from the standpoints of reference function. It is for this reason, it is necessary to discuss a bit about the way in which fuzzy sets are represented graphically in the literature references along with the new definition of complementation.

The remainder of the article is organized as follows. Section II defines the geometrical representation of fuzzy sets and some of its application areas. Section III deals with some of the papers related to fuzzy set theory. Section IV gives an overview of the new definition of complementation which is the main method to show how the representation becomes unacceptable from our standpoints. Finally, Section V presents our conclusions from this work and points to some potential areas for future works.

Before proceeding further with our suggested definition of complementation, we would like to discuss the works of other researchers in the field of fuzzy set theory who unlike us are of the opinion that there are some shortcomings in the theory concerned. Although these papers are still far from the main concern of our paper, it is worth mentioning them to support our claim.

• II.    Some Other Works Related to the Theory of Fuzzy Sets

Since Zadeh introduced the concept of fuzzy sets, a great deal of research has been conducted some of these are as follows:

M. Shimoda [2] presented a new and natural interpretation of fuzzy sets and fuzzy relations, but still did not change the fact that it could not satisfy all formulas of the classical set system.

• A. Piegat [3] presented a new definition of the fuzzy set: a fuzzy set A of the elements x is a collection of the elements which possess a specific property pA of the set and are qualified in the set by a qualifier QA using a qualification algorithm QA lg A . But nothing about essential shortcomings and mistakes of Zadeh's fuzzy

set theory and how to overcome them completely was discussed in it.

Qing-Shi Gao, Xiao-Yu Gao and Yue Hu [4]found that there is some mistakes Zadeh’s fuzzy sets and found that it is incorrect to define the set complement as , because it can be proved that set complement may not exist in Zadeh's fuzzy set theory. According to them it leads to logical confusion, and is seriously mistaken to believe that logics of fuzzy sets necessarily go against classical and normal thinking, logic, and concepts.Since they found some shortcomings in the Zadeh’s fuzzy set theory ,they wanted to move away from it and worked towards removing the shortcomings which according to them debarred fuzzy sets to satisfy all the properties of classical sets.They introduced a new fuzzy set theory,called C -fuzzy set theory which satisfies all the formulas of the classical set theory. The C -fuzzy set theory proposed by them was shown to overcome all of the errors and shortcomings, and more reasonably reflects fuzzy phenomenon in the natural world. It satisfies all relations, formulas, and operations of the classical set theory.

That is to say that these authors are also not satisfied with the way of defining the complemention of fuzzy sets.There are many such cases where the researchers found some sort of problems in the Zadeh’s fuzzy set theory some of which are mentioned above. Many other controversies exists too numerous to present here in details.

Like that of the aforementioned authors who had some doubts about the theory, we also want to convey that there seems some draw backs in the existing definition of complementation of a fuzzy set.It is for this reason we would like to review some of the results with special reference to the complementation of fuzzy sets.

In this article, we would like to rivisit the definition of complementation of fuzzy sets and in due course would like to replace it with a new one so that it becomes free from any doubt. It is important to mention here that in this article, we shall revisit the geometrical representation of fuzzy sets on the standpoints of the new definition. So before proceeding further, let us have a brief view of the geometrical representation of fuzzy sets. This will undoubtedly play an important role in narrowing down the gap that currently exists.

• III.    Geometrical Representation of Fuzzy Sets

In this section, we shall discuss in brief about the geometrical representation of fuzzy sets as proposed by Kosko ([5],[6]).

A hypercube is simply an n-dimensional space whose co-ordinate axes are of equal length. A unit hypercube is one in which the co-ordinate axes are of unit length. Lotfi Zadeh [1] for the first time suggested a geometric interpretation of fuzzy sets as point in unit hypercube.

A very interesting geometrical representation of discrete fuzzy sets was introduced by Kosko. He named it “set as points”. This approach identifies one fuzzy set with a point in an n- dimensional unit hypercube, where n is the number of elements in the universe of discourse.

Let us have a brief look at the geometrical representation in the following way;

Consider a universe of discourse containing two elements,

U = { x 1 , x 2 }

The Universal set is

represented by the point (1, 1) with the membership

U (X ) = 1    U (x2 ) = 1

function ^{A 1}      and ^{A 2}      . The point (1, 0)

represents the set

{ x ₁}

and the point (0,1) represents the

{ x } set ²

Similarly, a fuzzy set defined in that universe

_ 1       3 ,

A = {(xp-),( x2,-)} of discourse         55 is represented by the membership function and

1Ua (xi) = -

3Ua (x2) = -

Then the representation takes the following form

Table 1: Geometrical Representation of fuzzy sets

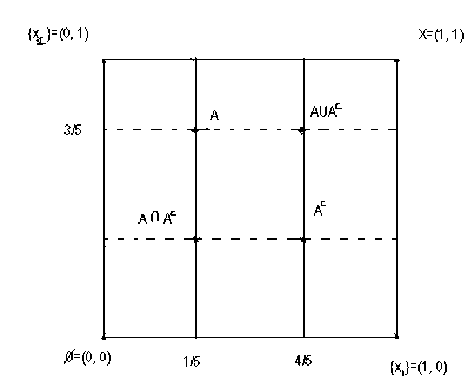
Then the point A can be represented as a point in two dimensional unit hypercube which is a square. This square represents all possible fuzzy sets of both elements; vertices of the square represent crisp set.

Kosko’s representation has become the cornerstone of fuzzy set theory. The uses of geometrical representation of fuzzy sets are many and varied in fuzzy areas. That is to say such representation had great potential applicability. One application area in which we can see the use of geometrical representation is the fuzzy entropy theorem. This fuzzy entropy theorem is the breakthrough concept. Entropy is the measure of uncertainty or disorder in a system. Within the geometrical framework of unit hypercube representations, the fuzziness of a set is determined by the distance of it from the nearest vertex. The idea that the fuzzy set located at the vertex has the zero entropy and the fuzzy set located at the midpoint has the maximum entropy, led Kosko to define fuzzy entropy in the following form:

Then this entropy theorem has been used in many important situations to draw conclusions. .It can be observed that the fuzzy entropy theorem, paved the way for fuzzy subsethood theorem. It was observed that the

power set of the fuzzy set B,

F (2 ) is the set of all

subset of B.

Here

F(2B)

defines a hyper rectangle

within a unit hypercube. With this in mind, the degree

to which a fuzzy set a, is A subset of another fuzzy set B is defined as the subsethood of A to B.

Mathematically, this is expressed as;

S(A,B)=

M(A∩B)M(A∪B)

E(A)=M(A∩Ac)

M(A∪Ac)

It was also mentioned that fuzzy subsethood is also used to define a simpler form for entropy in the following manner:

where A^c stands for the complement of the fuzy set A which is defined in the following manner:

E(A)=S(A∪Ac,A∩Ac)

µAc(x)=1-µA(x),∀x∈Ω

and M(A) stands for the cardinality of the fuzzy set A, which is expressed as:

M(A) =∑µA(x),x∈Ω

The geometrical interpretation of fuzzy entropy theorem which is the outcome of geometrical representation of fuzzy sets was presented in the following form:

Table 2: Geometrical Representation of Fuzzy Entropy Theorem

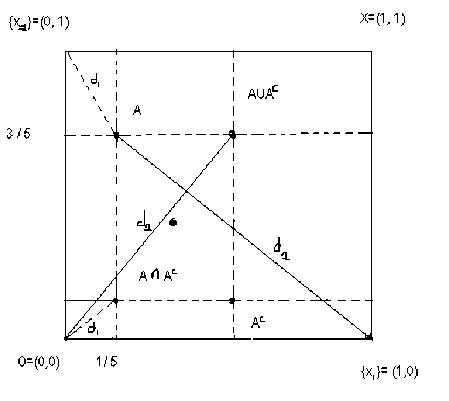
In he figure,

d

represents

M(A∩Ac)

and

d

2 represents

M(A∪Ac)

Thus from the above we can say that the geometrical representation of the fuzzy set played a vital role in the development of fuzzy entropy theorem and subsethood theorem, which are used in various fields to draw specific conclusions regarding various fuzzy situations. This very important theorem not only proved that fuzziness was real, but it derived Bayes theorem of probability as a special case of subsethood or fuzziness. It also states that to a certain degree, the universe of discourse is also contained in any of its subsets, which is an interesting interpretation of the concept of subsethood.

Although there are numerous applications of the aforesaid geometrical representation yet it is important to mention here that this representation cannot define nor represent fuzzy set of a continuos universe of discourse. Practically, it is very difficult to represent set with more than three elements.

the drawbacks which can be found in the current definition can be removed with the use of the current definition.

and

AA =Ω , the universal set.

• IV.    Baruah’s Definition of Complementation

Baruah ([7],[8] & [9]) has defined a fuzzy number N with the help of two functions: a fuzzy membership µ ( x )                     µ ( x )

function 2 and a reference function 1      such

0≤µ(x)≤µ(x) ≤1

that     12. Then for a fuzzy number

{x,µ(x),µ(x),x∈Ω denoted by     12         we would call

{µ(x)-µ(x)}

• ²¹as the fuzzy membership value, which is different from fuzzy membership function. As an illustration of the above formalization, we are going to mention the following few lines.

In accordance with the process discussed above, a fuzzy set defined by

A = {x, µ(x),x ∈ Ω}

would be defined in this way as

A = { x , µ ( x ),0, x ∈ Ω }

so that the complement would become

A^c = { x ,1, µ ( x ), x ∈ Ω }

The above expression shows how the membership functions are to be represented in terms of reference function.

Table 3: New definition of Complementation

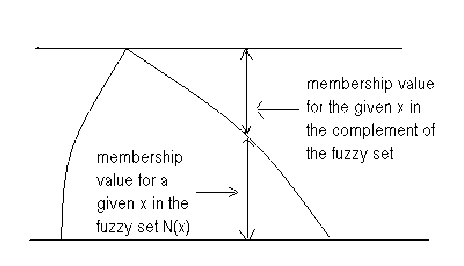
The above diagram gives us a very clear picture of the membership value recently introduced for the purpose of defining complementation of fuzzy sets.

The extended definitions using a reference function and with the help of appropriately defined union and intersection of such extended definitions lead to the assertion that for any fuzzy set A, we must have

AA =∅ ,the empty set.

In other words the two laws which were assumed to be true only for classical sets hold for fuzzy sets also. These two results obtained with the help of new definition of complementation not only encourage us to discard the existing belief that fuzzy sets violate excluded middle laws but also the proposed geometrical representation and all other results associated with it.

It is important to note here that in most cases of practical significance, it is desirable to consider reference function for fuzzy compliments. Fuzzy sets operation like union and intersection are also defined accordingly in order to keep pace with the aforesaid definition of complementation. All these results have been already considered and discussed in our previous works as can be found in Dhar ([10]- [20]). So we would not like to mention about all these in details herein.

This section has given a new representation of fuzzy sets with special reference to complementation that uses reference function which is essential if we are too make logical decision.

With this new definition of complementation, we would like to discard the well known geometrical representation of fuzzy sets with special reference to complementation and consequently the fuzzy entropy theorem and fuzzy subsethood theorem which were rooted in the geometrical representation of fuzzy sets.

Another result which stems from subsethood theorem is that the universe of discourse is a subset of any of its subset to some degree seems meaningless. It can be described by the fact that the universe of discourse is the superset of its subsets and so how it can be a subset of any of its own subset. It does not sound good from mathematical point of view. Here, we are not going to discuss about all these in details because these are already been discussed a lot in our previous works (see for example Dhar ([10]-[20]).

In other words, we would like to highlight the fact that if the geometrical representation is doubtful then all other results obtained with the help of this kind representation would surely be futile. The reason behind such a claim can be contributed to the fact in case of complementation, it is membership value not membership function which should be taken into consideration.

Another important thing worth mentioning here is that if we consider the new definition of complementation, then proper care should be given to the definition of cardinality of fuzzy sets. The reason is that when dealing with new definition, we should use membership value instead of membership function, Dhar [18]. Symbolically, it would take the following form:

M(A) = card(A)=∑{µ2(x)-µ1(x)},x∈Ω

This definition of cardinality would play a very important role in finding the cardinality of a fuzzy set defined on the basis of reference function. The main reason behind mentioning about the proposed definition of cardinality of fuzzy sets may be interpreted in the form that in many cases like finding entropy and subsethood, we can see that the use of the existing definition of cardinality but here we prefer to use the new definition of complementation of fuzzy sets and hence it is necessary to define it accordingly.

It can thus be mentioned that the geometrical representation can be discarded on two grounds: Firstly, due to some drawbacks in the existing definition of complementation and secondly, the definition of cardinality is also not properly defined.

• V.    Conclusions

The work began with a premise that the existing definition of complementation of fuzzy sets is not logical and hence the geometric representation of fuzzy sets should not be modelled in the way described. A new way of defining complementation of fuzzy sets is discussed herein.

In this article, we have studied certain basic concepts associated with fuzzy sets. In the process, it was found that the famous law of excluded middle and the law of contradiction hold well in fuzzy set theory unlike classical sets. It is the point for which the geometrical representation of fuzzy sets is to be reviewed. But the same geometrical representation can be carried out in case of usual fuzzy sets. Here efforts have been made to draw particular attention to the fact that the geometrical representation as well as the results associated with these types of representations has nothing to do if we refer to the new definition of complementation based on reference function. It is important to note here the fact that about finding entropy, we have discussed a lot in our previous works but regarding subsethood further works are necessary to find an appropriate result.

• [1]    Zadeh.L.A, Towards Theory of Fuzzy Systems, InAspects of Network and System Theory, R.E. Kalman N.D. Claris, New York: Holt, Rinehart and Winston, 1971.

• [2]    Shimoda M, A natural interpretation of fuzzy sets and fuzzy relations, “Fuzzy Sets and System”Vol.128, No.2, 2002.

• [3]    Pieget A, A new definition of Fuzzy sets , Int. J. Appl. Math. Comput. Sci., Vol.15, No1, 2005

• [4]    Qing-Shi Gao, Xiao-Yu Gao and Yue Hu, A new fuzzy set theory satisfying all classical set formulas, Journal of Computer Science and Technology, Vol.24, No.4, 2009.

• [5]    Kosko.B, Neural Networks and Fuzzy System, A Dynamic System Approach to Machine Intelligence, Eagle Wood Cliffs, Ng, Prentice Hall, 1992.

• [6]    Kosko.B, Fuzziness Vs Probability, Int. J. General System, Vol. 17, 211-240 , 1990.

• [7]    Baruah. H.K, Fuzzy Membership with respect to a Reference Function ,Journal of the Assam Science Society, Vol.40,No.3, ,65-73, 1999.

• [8]    Baruah.H.K, Towards Forming a field of Fuzzy sets, IJEIC, Vol. 2, Issue 1, 16-20, 2011

• [9]    Baruah H.K, Theory of Fuzzy sets Beliefs and Realities , IJEIC, Vol. 2 ,Issue 2,1-22,2011

• [10]    Dhar .M, Hwang and Yang’s definition of Entropy of Fuzzy sets, IJLTC, Vol.2, No.4, 496-497, 2011.

• [11]    Dhar.M, Fuzzy Sets Towards Forming Boolean Algebra , IJEIC, Vol.2, Issue 4,137-142, 2011.

• [12]    Dhar.M, On Separation Index of Fuzzy Sets, IJMA, Vol.3, No.3, 932-934, 2012.

• [13]    Dhar.M, On Geometrical Representation of Fuzzy Numbers, IJEIC, Vol.3, Issue 2, 29-34, 2012.

• [14]    Dhar.M, On Fuzzy Measures of Symmetry Breaking of Conditions, Similarity and Comparisons: Non Statistical Information for the Single Patient., Accepted for publication in IJMA journal, 2012.

• [15]    Dhar.M, A Note on Subsethood measure of Fuzzy sets, accepted for publication in IJEIC in August, Korea.

• [16]    Dhar. M, Representation of fuzzy matrices Based on Reference Function, I.J. Intelligence Systems and Applications, 2012, 5(2), 84-90.

• [17]    Dhar.M, A Note on Determinant and Adjoint of Fuzzy Square Matrix ,accepted for publication in IJISA

• [18]    Dhar.M, On Cardinality of Fuzzy sets, accepted for publication in IJISA

• [19]    Dhar M, On Some properties of entropy of fuzzy numbers, accepted for publication in IJISA

• [20]    Dhar.M, A Note on existing Definition of Fuzzy Entropy, IJEIC, Vol.3, Issue 1,17-21, 2012.

Mamoni Dhar is an Assistant Professor in the department of Mathematics, Science College, Kokrajhar, Assam, India. She received M.Sc degree from Gauhati

University, M.Phil degree from Madurai Kamraj University, B.Ed from Gauhati University and PGDIM from Indira Gandhi National Open University. She also received National Scholarship from Matriculation to Post Graduation. Her research interest is in Fuzzy Set Theory from new perspectives. She has published eighteen articles in different national and international journals.