On the construction of stress discontinuity lines for a two-dimensional plastic region

A stress discontinuity line is a certain line (surface) in the body on which stresses undergo discontinuity. The reason for the appearance of discontinuities in plane stress is the overdetermination of the boundary value problem in the vicinity of a singular point on any one side of the contact boundary. As a rule, the discontinuity lines are located in a stronger part of the joint [1–2]. When studying the critical state and the strength of structures, this phenomenon must be taken into account. The same applies to bar structures [1–5] and thin-walled cylindrical shells, where the boundary value problem is also overdetermined. The problem becomes more complicated if the strip material is inhomogeneous in the weaker and/or stronger part of the joint [6].

To construct lines of stress discontinuity, in case of plane strain, it is necessary to take into account that they are located at the intersection point of the lines of characteristics of one family and are directed along the angle bisector formed by these characteristics. Therefore, to find these lines, it is necessary to construct characteristics. The easiest way to do this is for the torsion problem, since in this case the characteristic is directed along the normal to the outer contour and finding the sliding lines and their intersection points is quite simple. This is the subject of research of a sufficient number of works on the plastic torsion of isotropic cylindrical and prismatic bars in case when the side surface of the bars is free from tangential loads, as well as in case when the side surface of the bar is under the action of external variable pressure [7; 8]. The torsion of anisotropic cylindrical and prismatic bars was studied in [9–11]. In [12], the limiting state of the sector of an anisotropic circular ring under torsion is determined. In [13], the construction of characteristic fields for a cylindrical bar along an arbitrary yield surface is shown. In [14–17], the surfaces of strain discontinuities in elasto-plastic media were considered.

For problems of plane deformation of a plastic material, it is not easy to construct discontinuous solutions. This is due to the need to consider two families of characteristics and the complexity of constructing these sliding lines. To solve this problem, we construct a continuous deformation of two exact solutions: a homotopy of the Prandtl and Nadai solutions. Let us find the points of intersection of the sliding lines of one family and construct the discontinuity lines.

Homotopy of Prandtl and Nadai Solutions

Let us consider the Tresca-Saint-Venant-Mises system of flat ideal plasticity, which consists of two equilibrium equations and the plasticity condition:

'°- + 2^ = о,       7° = о, дx   ду        дx   ду

(°x -°у)2 + 4Т2у = 4k2, where σx, σy, τxy are the stress tensor components; k is the yield strength in pure shear. According to the replacement continued by M. Levy

° _x = ° - k sin 2 0 ,

° y = ° + k sin 20, т xy = k cos 20, system (1) is reduced to a quasilinear system:

д° э,Гд0 ™  30 . .3„

2 k —cos 20+sin20l = 0, дx    у дx        ду д° ./д0д0

2 k —sin20 +cos20l = 0, ду     удx        ду where о is the hydrostatic pressure; 0--is the angle between the first principal direction of the stress 4

tensor and the OX axis.

The Prandtl solution is often used to describe the compression of a rigid plastic material by rough plates. It is assumed that the length of the layer is much bigger than its thickness. This solution approximately describes the real situation at some distance from the center of the layer, if the origin of coordinates is located in the center of the layer.

In terms of variables σ, θ for system (2), this solution has the form

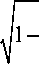
^y h ²

x

° = ^- P i ^- k T h

у=hcos20, where h = const; y = ±h are plate boundaries; p1 = const.

The boundary solutions take the form

0| у = h = n n , n eZ ,

°| у = h =- P i ^{- k}x .

h

The characteristics of the solution are as follows:

x = h(20- sin20) - h I 2c + -p1 l, у = ±h cos20, i = 1,2, у      k J where ci is const.

The Nadai solution describes the plastic position around a round hole of radius R, loaded with a uniformly distributed normal pressure p1 = const and zero shear stress on the hole contour. This solution can be written as n 0 = Ф + 7, 4

2     2                        2

x + у              r

° = - p , + k + k In--- :— = - p , + k + k In— г,

2 _R 22 _R 2

where r ; φ are polar coordinates.

The boundary conditions take the form

⁰| r = r =Ф + П , ^a| r = R = P 2 ^{+ k} .

The resulting sliding lines look like this:

ф = 0 - П, r = Rexp ±0 + ——-

4,       4     2 k where ci – const; i = 3,4.

Let us express the solution of Nadai and Prandtl as a solution of a linearized system:

P 2 - k

I n

x = cos I0 - I Re 2k

a e2k,

P 2 - k

. I . П 1

y = sin 0 - Re ² k

I 4)

a e2k,

h a Ph x =---¹— h sin2 0 ,

kk y = hcos20 .

We perform a homotopy linear combination of the Prandtl and Nadai solutions:

I h a   P 1 h

x = a -   -   -

kk

P 2 ^{- k}

h sin2 0| + ( 1 - a ) sin |0-ⁿI Re ^{2 k}

a e2k,

P 2 ^{- k}

I П y = h cos20- (1 - a )cosI0-—I Re 2 k

a e2k,

where a is a group parameter.

We get the boundary curve for solution (10):

n

a = - P1 + k;   0 = ф + —.

Substituting σ = 2 k ( a + θ) into system (3), we obtain the parametric equations of the sliding lines family:

x = ah I 2(c1 +0) + P1

P 2 ^{- k}

+ sin20| + (1 - a ) Re 2 k cos |0-nI ea+0 ,

P 2 - k

y = ah cos2 0 + (1 - a )Re ^{2 k} sin I 0-

П | e^a +0 4 J

.

In this case, we can observe the evolution of characteristics that depend on the group parameter a ; for a = 1, we obtain the characteristics of the Prandtl solution (Fig. 1).

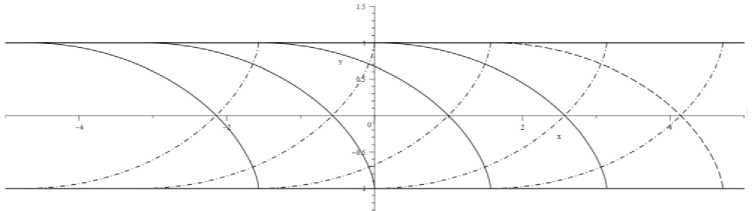
Fig. 1. Transformed sliding lines: h = 1; p 1 = p 2 ; a = 1

Рис. 1. Преобразованные линии скольжения: h = 1; p 1 = p 2 ; a = 1

For a = 0, the characteristics of the Nadai solution are shown in Figs. 2.

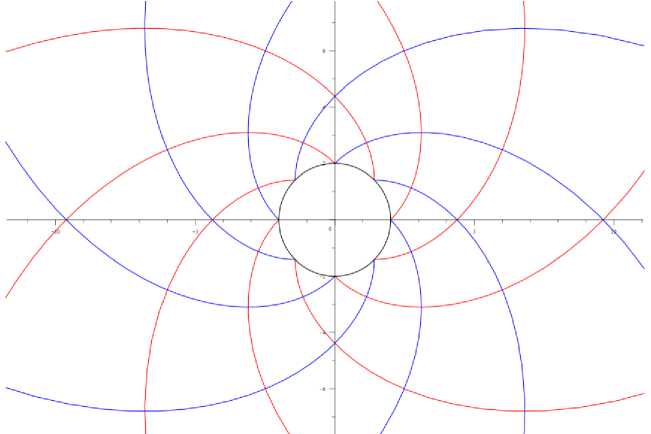
Fig. 2. Transformed sliding lines: a = 0

Рис. 2. Преобразованные линии скольжения: a = 0

At a = 0.5, the characteristics of one family begin to intersect and lines of stress discontinuity appear, as in Fig. 3.

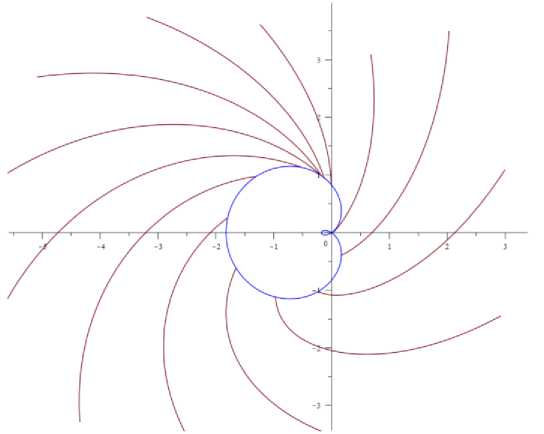
Fig. 3. The intersection of the sliding lines for the hole in the form of the Pascal snail a = 0,5

Рис. 3. Пересечение линий скольжения для отверстия в виде улитки Паскаля a = 0,5

Since the characteristics of one family intersect, the values along them are different, and the solution of the Cauchy problem after the intersection point cannot be continued continuously, a line of stress discontinuity appears. This line of discontinuity passes along the bisector of the angle formed by the intersecting characteristics and exits from the point of their intersection in coordinates [–0.183; 0.991] (Fig. 4).

Fig. 4. Stress discontinuity line

Рис. 4. Линия разрыва напряжений

Conclusion

In this paper, we construct a homotopy of two known exact solutions: that of Prandtl and of Nadai, i.e., a continuous transformation of one solution into another. In this case, one can observe the evolution of characteristics that depend on the group parameter a : for a = 1, the characteristics of the Prandtl solution are obtained; for a = 0 – the characteristics of the Nadai solution; at a = 0.5, the characteristics of one family begin to intersect and lines of stress discontinuity appear, which pass along the bisector of the angle of intersection of the characteristics and exit from the point of their intersection. If we continue to increase the parameter α, the number of intersecting characteristics also increases, which complicates the construction of the stress discontinuity line. The solution of this problem will be considered in further works.