On The Edge-balance Index Sets of the Power Circle Nested Graph C_(7^m)×P_(m_7) (m≡2(mod3))

Published Online June 2014 in MECS

• I .    I NTRODUCTION

  Graph labeling problem starts from A. Rosa’s famous beautiful tree conjecture in 1966. Balance index sets are an important branch of graph labeling problem. Boolean index [1] set of graphs is that makes the vertex sets and the edge sets of graphs through the mapping function with Z ₂ , to study the characteristics, inherent characteristics of graphs, the structure and design techniques, and to complete the theoretical derivation of the index sets of graphs and formula proof. Balance index set [2] is an important branch of Boolean index sets, edge-balance index set is one of important issues of balance index sets. Its theory can be applied to information engineering, communication network, computer science, economic management, medicine, etc.

Before the years 2006, people mainly studied the edgebalance index of the finite graph. Since 2007, Yuge Zheng with her students has been committed to the research about the edge-balanced index sets of the graphs. In 2008-2009, Juan Lu has completely solved the edgebalance index sets of the series of the infinite chain graph. In 2009, Yurong Ji and M. C. Kong with his partners used the different methods to solve the edge-balanced index sets of the complete graph, respectively in reference [3] [4]. In 2010-2012, Professor Zheng told Ying Wang and Jingjing Yao to completely solve the edge-balance index sets of the equal-cycle nested graph, for details, please refer to [5] [7]. In 2011-2012, elder sister Hongjuan Tian, Yanming Chang and Qingwen Zhang started to research infinite power-cycle nested graph in reference [6], and completed for n=2,3,4,6,8. The larger the value of n is, the more difficult the research of the graph design of odd n is, using the innovation of this mosaic design and the method of the foundation drawing validation. At the same time, using the foundation drawing and toothed nested-cycle graph, we completed the labeling design of the edge-balance index sets of C 7m xPm graphs and formula derivation.

The rest of this article is organized as follows. In the second part, we give the definitions which will use in this paper. In section 3 we summarize the main results and give a brief overview of the key ideas of their proofs. The main theorem is presented in the fourth section. In the fifth part of the paper, we draw the conclusion.

• II.    P RELIMINARY N OTES

In graph G , the edge set of labeled 0 or 1 is recorded as E (0) or E (1) , using e (0) , e (1) to present the number of E (0) , E (1) . The vertex set of labeled 0or 1 is recorded as V(0) or V(1) , using v(0) , v(1) to present the number of V(0) , V(1) .

In graph G , let f: E(G) ^ Z2 is an edge labeling function, That is to say, ^e e E(G), f (e) = 0or1 . According to the edge labeling f , we define an associated partial vertex labeling f+ : V(G) ^ Z2 , as

0, e x (0) >  e x (1)

follow:

f ⁺ ( x ) H

1, e x ⁽¹⁾ >  e x ⁽⁰⁾      , ^where e v ⁽⁰⁾

is

unlabled , e_x (0) = e_x (1)

the cardinality of the set {e e E(G) : v(e) = 0} , ev (1) is the cardinality of the set {e e E(G) : v(e) = 1} .

Definition 1 An edge labeling f : E(G ) ^ {0,1} of the graph G is said to be edge-friendly if e y (0) — e^ (1)| ^ 1 .

Definition 2 If there is an edge-friendly labeling in a graph, {| V y (0) - V y (1)|: f is an edge friendly labeling of

G } is called on edge-balance index of G and denoted by EBI ( G ) . Specifically, the maximum of edge-balance index denoted by max{ EB ( I G )} .

Definition 3 P represents that every road contains m m ₇

points, and that there are 7 branches at any points except the terminal point of each road.

Definition 4 C m shows the graph contains m cycles, the cycles are denoted by the first cycle, the second cycle, the third cycle,      , the m-th cycle from the inner cycle to the outer. And there are 7i vertices on the i-th cycle.

Definition 5 The nested graph with power-cycle is the embedded graph including C m and P , denoted by

' 7 m        m 7 .

Example. Fig. 1 illustrates two graphs of C x P

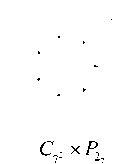
Fig. 1. two graphs of C 7_m ^x P m

For convenience, we will have the following label for the nested network graph: The vertices of the most inner circle in clockwise order are labeled as follows: (1) ,(1) , ,(1) ,(1) ; Similarly, from inside to outside the vertices of the most outside circle in clockwise are labeled as follows: ( m ) ,( m ) ,( m ) ,( m ) , ,( m ) m ,( m ) m .

Among them, symbols ( j ). says the i - th vertex in the j - th circle. The paths begin with the vertex (1)_x , as follows:

• (1) 1 ^ (2) , ^ (3) , ^ ^ ( m - 1) 1 ^ ( m\ ;

• (1) , ^ (2) 1 ^ (3) 1 ^-^ ( m - 1) 1 ^ ( m )₂;

• (1) 1 ^ (2) 1 ^ (3) 1 ^-^ ( m - 1) 1 ^ ( m ) m ;

• (1) 1 ^ (2) 1 ^ (3) 1 ^-.^ ( m - 1)₁ ^ ( m ) m + 1 ;

• ⁽¹⁾ 1 ^ ⁽²⁾ n 1 ^ ⁽³⁾ n 2 ^> ⁽ m - 1) n m - 2 ^ ^{( m )} n m - 1 -1 ;

• (1) 1 ^ (2) _n 1 ^ (3) n 2 ^-^ ( m - 1) n m - 2 ^ ( m ) n m - 1 ;

similarly, the paths begin with the vertex (1) , as follows:

• (1)    n ^ (2) „ 2 _ n + 1 ^ (3) n 3 - ,+1 ^^ ( m - 1) n m - 1 - n m - 2 + 1 ^ ( m ) n m - n m - 1 + 1

• (1)    n ^ ( ² ) .- n + 1 ^ ( ³ ) n 3 - n 2 + 1 ^-^ ( m - ¹ ) n m - 1 - n m - 2 + 1 ^ ( m ) n m - n m - 1 + 2

⁽¹⁾ n ^ ⁽²⁾ n 2 - n + 1 ^ (3) n 3 - n 2 + 1 ^     >  ⁽ m ^{- 1)} n m - 1 - n m - 2 + 1 ^ ⁽ m ) n m _ n m - 1 + n

• ⁽¹⁾    n ^ ⁽²⁾ n 2 - n + 1 ^ ⁽³⁾ n 3 - n 2 + 1 ^-^ ⁽ m ^{- 1)} n m - 1 - n m - 2 + 1 ^ ⁽ m ) n m - n m - 1 + n + 1

(1)n ->(2)n2 ^(3)n3 ^•••^(m-1)nm-1 ^(m)nm-1 ;

(1) n ^ (2) n 2 ^ (3) n ^...^ ( m - 1) n m - 1 ^ ( m ) n m ;

The above says that the C m x p have n^m paths.

Definition 6 A 1-vertex x is considered to be saturated, if the n edges linked to x satisfy e_x (1)= e_x (0)+1 , when n is an odd number; e (1)= e (0)+2 ,when n is an even number ;otherwise, the 1-vertex x is unsaturated. A 0-vertex x is considered to be saturated, if the n edges linked to x are all 0-edges; otherwise, the 0-vertex x is unsaturated. A vertex x is considered to be empty, when the point x satisfy e_x (1) = e_x (0) .

Under the definition of power-cycle nested graph, in order to more convenient to figure symbols function. According to the recursive nature of power-cycle nested graph, given the concept of the clawed nested-cycle subgraph.

Definition 7 In the power-cycle nested graph, the induced sub-graph of the vertices, which the ray paths through the points with the vertices on the k(t - 1) + i cycle as starting points and the vertices on the kt + i cycle as the terminal points, denoted by V ^' . And the graph V_t ' subtract the edge on k(t - 1) + i is thought as m - i_x the clawed nested-cycle sub-graph V ( t = 1,2, • • •,----) .

tk

Specifically, k be decided by the m classification. In the graph C^ m x p ^ ( m >  5) , refers to all the clawed nested-cycle sub-graphs are the clawed 3 nested-cycle sub-graph.

Under the definition of the clawed nested-cycle subgraph, in order to more convenient to figure symbols function. According to the dual nature of power-cycle nested graph, given the concept of the fan-shaped subgraph.

Definition 8 For a given the clawed nested-cycle sub-л                      m -ix л i i graph V (t = 1,2, • • •,-----), based on the starting points of tk

,              ,               _ m -ix, the ray paths, V(t = 1,2<--,-----) is divide from the tk middle the fan graphs, if the starting point in the a circle, it can be divided into ka sector fan-shaped graphs, denoted by H3,H„...,Hкй .

Specifically, every the fan sub-graph of the single point does not include its own point.

According to the definition of the clawed nested-cycle nested sub-graph, all of the clawed nested-cycle nested sub-graph V(t = 1,2,-••,m—i) (i = 5,6,7) are 3 nested-tk cycle nested sub-graph in the CT x P7 (m > 5) . So if given the clawed nested-cycle sub-graph starting point in the a circle, the corresponding the clawed nested-cycle sub-graph can be divided into 7a sector fan-shaped graphs.

In order to more convenient to figure symbols function, we introduce the concept of divisibility for power-cycle nested      graph,      it      is      obvious      that

( m - 2   Л

C 7 m ^X P m 7 = C 7 K X P k 7U

Vt t=0

according to the 3

circles of the t nested-cycle nested sub-graph V , from the side to the out, in turn, for the a circle, the a + 1 circle, the a + 2 circle; V_t will be average divided into 7 3 t ^{+ 2} sector fan-shaped sub-graph H , ensure that each H has the 7 ⁱ point and the 7 ⁱ edge on the i circle , according to the clockwise order the points on the i circle denoted by ( i ) ,( i ) ,   ,( i ) i .

For the edge-friendly labeling of the graph C m x P ₇ ( m - 5) . We discuss the edge-balance index set of this graph from the following three parts: m = 0(mod3) , m = 1(mod3), m = 2(mod3) . But, in this paper, we only research it when m = 2(mod3) .

• III.    L EMMAS A ND P ROOF

Lemma 1 In the graph C m x P , for the fan subgraph H _o of the single point, max{ EBIH₀ } = 323 .

Proof : Because each part in the fan sub-graph of the single point have equal features, here we only give label H , the others label as well as itself.

There are 798 edges in the fan sub-graph H of the single point, because of | e (0) - e (1)| <  1, there are 399 0-edges. To put it simply, we only mark the 0-edges of the fan sub-graph H of the single point, the left edges are 1-edges.

The four edges are all 0-edges except ( a )₆( a )₇,( a )₅( a )₆,( a )₄( a )₅ in the a circle, and the 7² edges are all 0-edges in the a + 1 circle. The edges linked to the vertices ( a )(1 <  i <  3) are all 0-edges in the a circle; The edges linked to the vertices (a + 1)(1 <  i <  24,29 <  i <  32,39 <  i <  42,47 <  i <  49) are all 0-edges in the a + 1 circle; The 0-edges between the a circle and the a + 1      circle:      ( a ) ( a + 1).

(i = 4,22 <  j <  24)( i = 5,29 <  j <  32)( i = 6,3 9 <  j <  42) (i = 7,47 <  j <  49) ; The 0-edges between the a + 1 circle and the a + 2 circle:    ( a + 1).( a + 2).

(j = 7(i-1) + k,i = 25 + 2/,0 < l < 1,4 < l < 6,9 < l < 10,k = 1,2) (j = 7i + k,i = 26 + 2/,0 < l < 1,4 < l < 6,9 < l < 10,k = -1,0)  ; In the a + 2 circle the edges are all 0-edges: (a+2)(a+2)г+1    (i = 170+7 k+j, k = 2l ,0 < l < 1,4 < l < 6,9 < l < 10, j = 1,3,5,7,9)

Then v (0) = 38 , | v (1) - v (0)| = | v - 2 v (0)| = 323 .

We can get the edge-friendly labeling of the fan subgraph H of the single point by calculation, then not conclude the vertices are not defined and unsaturated. When we change the 0-vertex into 1-vertex or undefined vertex, we must take out five 0-edges. Thus, wherever we put the five 0-edges, the number of the 0-vertex will increase, meanwhile the number of the 1-vertex will not increase. So 323 is the maximum edge-balance index.

So max{ EBIH } = 323 .

Lemma 2 For the power-cycle nested graph C x p ^ , when m = 5, max{ EBI ( C ₅ x p )} = 15873 .

Proof: There are 39207 edges in the power-cycle nested graph C ₅ x p , because of | e (0) - e (1)| <  1, there are 19603 0-edges. To put it simply, we only mark the 0-edges of the graph, the left edges are 1-edges.

The edges are all 0-edges in the 2 circle and in the 3 circle and in the 4 circle. In the 1 circle the edges are all 0-edges: (1) 2 (1) 3 ,(1) 4 (1) 5 ,(1) 6 (1) 7 ,(1) 7 (1) 1 .

First of all, edges in all the paths which set out from the labeled point (1) : the edges linked to the vertices (2) (1 <  i <  3) are all 0-edges in the 2 circle; The edges linked to the vertices (3)(1 <  i <  23)( i = 33 + j ,1 <  j <  4)( i = 48,49) are all 0-edges in the 3 circle; The 0-edges between the 2 circle and the 3 circle:

(2) 4 (3) ,(i = 22,23)     , (2)₅(3) , ( i = 34,35)     ,    (2) 6 (3) , ( i = 36,37)    ,

(2)7(3) i (i = 48,49);

The edges linked to the vertices

(4)(1 < i < 163)(i = 173 + 7k + j, k = 2l,0 < l < 3, j = 1,2,3,4) (i = 271 + 7k + j,k = 2l,0 < l < 3, j = 1,2,3,4)(230 < i < 261) (328 < i < 343) are all 0-edges in the 4 circle; The 0-edges between the 3 circle and the 4 circle: (3).(4)/j = 7(i -1) + k,i = 24 + 2l,0 < l < 4,7 < l < 11,k = 1,2) (j = 7i + k,i = 25 + 2l,0 < l < 4,7 < l < 11,k = -1,0)  ; The 0- edges between the 4 circle and the 5 circle: (4) (5)

( j = 7( i - 1) + k , i = 164 + 2lor 262 + 2 l ,0 <  l <  4,7 <  l <  11,

• 14 <  l <  18,21 <  l <  25,28 <  l <  32, k = 1,2)   ( j = 7 i + k , i = 165 + 2lor 262 + 2 1 ,

0 < l < 4,7 < l < 11,14 < l <  18,21 < l <  25,28 < l <  32, k = - 1,0)   ; In the 5

circle the edges are all 0-edges    (5) i (5) i _{+ 1}

( i = 1143 + 7 k + jor1829 + 7 k + j , k = 2 l ,0 <  l <  4,7 <  l <  11, 14 <  l <  18,21 <  l <  25,28 <  l <  32, j = 1,3,5,7,9) .

The second, edges in all the paths which set out from the labeled point (1) : the 0-edges between the 1 circle and the 2 circle: (1)₇(2).(43 <  i <  49); The edges linked to the vertices (2).( i = 43,44) are all 0-edges in the 2 circle; The edges linked to the vertices (3)(295 < i < 308)( i = 315,316)( i = 329,330,343) are all 0-edges in the 3 circle; The 0-edges between the 2 circle and the 3 circle: (2) 45 (3) 315 ,(2) 46 (3) 316 ,(2) 47 (3) 329 ,(2) 48 (3) 330 ,(2) 49 (3) 343 ; The edges linked to the vertices (4) (2059 <  i <  2158)

(i = 2168 + 7k+j,k = 2l,0 < l < 2, j = 1,2,3,4) (i = 2224 + 7k+jor2322+7k+j, k = 2l ,0 < l < 4, j = 1,2,3,4) (2201 < i < 2214)(2295 < i < 2312) (2393 < i < 2401)

are all 0-edges in the 4 circle; The 0-edges between the 3 circle and the 4 circle: (3),(4)_y( j = 7i + k , i = 310 + 2 l ,

0 <  l <  2,4 <  l <  9,11 <  l <  16, k = - 1,0)( j = 7( i - 1) + k , i = 309 + 2 l ,0 <  l <  2,4 <  l <  9, 11 <  l <  16,k = 1,2) ;

The 0-edges between the 4 circle and the 5 circle: (4) i (5) j

( j = 7( i - 1) + k , i = 2159 + 2 l ,0 <  l <  4,7 <  l <  11,

14 <  l <  18,k = 1,2)

( j = 7 i + k , i = 2160 + 2 l ,0 <  l <  4,

7 <  l <  11,14 <  l <  18,k = - 1,0)

(j = 7(i -1) + k, i = 2215 + 2l or2313 + 21,0 < l < 4,7 < l < 11,14 < l < 18,21 < l < 25,

28 <  l <  32,35 <  l <  39,k = 1,2)

(j = 7 i + k, i = 2216 + 2l or2314 + 2l,0 < l < 4,7 < l < 11,14 < l < 18,21 < l < 25,

28 <  l <  32,35 <  l <  39,k = - 1,0)

( i = 2159,15107 <  j <  15113) ( i = 2160,15114 <  j <  15120) ;

In the 5 circle the edges are all 0-edges: (5)z(5)i+i( i = 15500 + 7k + jor16186 + 7 k + j, k = 2l ,0 < l < 4,7 < l < 11,14 < l < 18,21 < l < 25,28 < l < 32,35 < l < 39, j = 1,3,5,7,9)

( i = 15134 + 7 k + j , k = 2 1 ,0 <  l <  2,5 <  l <  9,12 <  l <  16, j = 1,3,5,7,9)

The last, the label methods of the point (1)(2 <  i <  6) set out the paths’ edge is the same as the point (1) .

Then v (0) = 1867,| v (1) - v (0)| = | v - 2 v (0)| = 15873 .

In this structure graph, the degree of the vertices is 9 on the first cycle, the degree of the vertices is 10 on the second and third cycle and fourth cycle, the degree of the vertices on the fifth is 3. In the 1867 0-vertexes, the vertices are all saturated, except the vertices (4)₂₁₅₉,(4)₂₁₆₀ . Therefore, in order to change the labeling of the 0-vertexes, we need to interchange 5 0-edges and 5 1-edges. It is obvious that the interchanging must bring that the value of v (0) increases or remains unchanged, and the value of v (1) certainly decreases. So the value of |v (0) - v (1)| reduces.

Then the value of | v (0) - v (1)| is maximum in the aforementioned structure graph, so max{ EBI ( C 5 x p )} = 15873.

Lemma 3 For the power-cycle nested graph C x P , when m = 2(mod3) and m >  5 ,

m

max{EBI(C7. x Pm7)} = ———

18

_p . Tb        7 ^{m + 1} - 28

Proof: There are edges in the power-cycle

nested graph C x P, because of |e(0) -e(1)| < 1, there are

, m + 1

0-edges.

When m = 5 , the formula can be proved by lemma 2.

When m > 8 , as the foundation graph C5 x p by lemma 1, denoted by Uo = C5 x p ,

( m - 2

C 7 m x P m 7 = U ₀U U ^

= U0U75 H0U78 HoU-U7 m -3 H0

Each of the vertices of the outer circle be seen as the starting point to make the graph H in the figure C m - 3 x P m -3₇ , there are 7 m 3 H 0 . In this graph C^ x P m^ ,

m v (0) = (7m-3 + 7m- 6 +••• + 78 + 75) x 38 +1867 = 7-----

1 v (1) - v (0)| = v - 2 v (0)| =

7 m + 1 - 7     7 m - 4 --2 x----- 69

_ 17 • 7 m - 5 =    18

In this structure graph C^ x P^ , the degree of the vertices is 9 on the first cycle, the degree of the vertices is 3 on m cycle and all of the others are 10. All of the 1-vertexes are saturated, except the vertices (4)₂₁₅₉,(4)₂₁₆₀ . The edges linked to the other 0-vertexes are all 0-edges. Therefore, in order to change the labeling of the 0-vertexes, we need to interchange 5 0-edges and 5 1-edges. It is obvious that the interchanging must bring that the value of v (0) increases or remains unchanged, and the value of v (1) certainly decreases. So the value of |v (0) - v (1)| reduces.

So for the power-cycle nested graph C^ x P_m , when

,    . .                                 _   17 • 7m - 5

m = 2(mod3) m >  5, max{ EBI ( C x P )} =-------- .

7     m7          18

Specifically, Each of the vertices of the outer circle be seen as the starting point to make the graph H in the figure C^m _{- 3} x P ₃ , the label of each starting point is the same as the boundary point of five laps foundation figure, and it stays the same.

Lemma 4 For the power-cycle nested graph C^m x P_m , when m = 5 ,{15872,15871,--,1,0} c EBI ( C 5 x P ₅ ).

Proof :   In the following proof, we use

(2 k - 1)_r(2 k)_s ^ (2 k X(2 k X₊₁ to present that the edge (2 k - 1)_r(2 k)_s is from 0-edge into1-edge, at the same time the edge (2 k ) (2 k ) is from 1-edge into0-edge. Among them, we use (5).(6)_7z. ^ (6)_7z(6)_7z+i to present that the edge (5) (6) is from 1-edge into 0-edge, at the same time the edge (6) (6) is from 0-edge into 1-edge.

First, build an odd index set:

Step1: (4) , .(5) j + 7( i _₀ ^ ⁽⁵⁾ j + 7( i - 1) ⁽⁵⁾ j + 7( i - 1) + 1

( i = 1,-,163, j = 1,-..,4)

and

(5) , (6) 7 , ^ (6) 7 , (6) 7 , + 1

( i = j + 7( k - 1), k = 1,---,163, j = 2,•••5)   , we can get

I v (1) - v (0)| = | v - 2 v (0)| = {15871,15869,-•-,14569}

Step²:  (4) i (5) j + 7(, _ 1) ^ (5) j + 7₍ i - 1) (5) j + 7( i - 1) + 1

( i = 230,-•-,261, j = 1,---,4)

and

(5) i (6) 7 i ^ (6) 7 i (6) 7 i + 1

( i = j + 7( k - 1), k = 230,••*,261, j = 2,---5)   , we can get

| v (1) - v (0)| = v - 2 v (0)| = {14567,14565,- • -,14313}

Step3: (4) (5) j + 7( i - 1) ~ (5) j^i — ,)⁽⁵⁾ j + 7( i - 1) + 1

( i = 328,-",343, j = 1,---,4)

and

(5) i (6) 7 i ^ (6) 7 i (6) 7 i + 1

( i = j + 7( k- 1), k = 328,---,343, j = 2,---5)   , we can get

I v (1) - v (0)| = | v - 2 v (0)| = {14311,14309,- -,14185}

Step⁴: (4) , .(5) j ₊₇₀_₀ ^ (5) j ₊ 7( , _ 1₎ (5> j + 7( i __{0+ l}

(i = 173 + 7n + m,n = 2l,0 < l < 3,7 < l < 10,m = 1,-4, j = 1,-4)

and

(5),(6)7i ^ (6)7/(6)„+1(i = j + 7(k -1), k = 173 + 7n + m,n = 2l,0 < l < 3,7 < l < 10,m = 1,-,4, j = 2,---,5) , we can get |v(1)-v(0)| = |v-2v(0)| = {14183,14181,---,13929}

Step⁵ (4) i (5) j _{+ 7}( , - 1₎ ~ (5) j + 7(i - 1) (5) j + 7( i - 1) + 1

( i = 164 + 2 lor 262 + 2 l ,0 <  l <  4,7 <  l <  11,14 <  l <  18,21 <  l <  25, 28 <  l <  32, j = 1,2)

and

(5) i (6) 7 i ^ (6) 7 i (6) 7 i + 1

( i = j + 7( k - 1), k = 164 + 2 lor 262 + 2 l ,0 <  l <  4,7 <  l <  11,

14 <  l <  18,21 <  l <  25,28 <  l <  32, j = 2,3) , we can get

I v (1) - v (0)| = | v - 2 v (0)| = {13927,13925,-•-,13729}

Step6: (4) i (5) j + 7( i -₀ ^ (5) j + 7( i -₀(5) ji -_D+ 1

( i = 165 + 2lor 263 + 2 l ,0 <  l <  4,7 <  l <  11,14 <  l <  18,21 <  l <  25, 28 <  l <  32, j = - 1,0)

and

(5) i (6) 7 i ^ (6) 7 i (6) 7 i + 1

( i = j + 7 k , k = 165 + 2lor 263 + 2 l ,0 <  l <  4,7 <  l <  11,

14 <  l <  18,21 <  l <  25,28 <  l <  32, j = 0,1) , we can get

I v (1) - v (0)| = | v - 2 v (0)| = {13727,13725,-•-,13529}

Step7: Similar to the first, second, third, fourth, fifth, sixth step transformation, we can obtain these labeled graphs of edge-balance indexes which are {13527,13525,  ,1809}

Step8: (4) i (5) j + 7( i - 1) ^ (5) j _{+ 7(} i -„(5) j _{+ 7(} i - 1) + 1

( i = 2059,-,2158, j = 1,---,4)

(5) i (6) 7 i ^ (6) 7 i (6) 7 i + 1

( i = j + 7( k - 1), k = 2059,---,2158, j = 2,---5)   , we can get

I v (1) - v (0)| = | v - 2 v (0)| = {1807,1805,-• ,1009}

Step9: (4) i (5) j _{+ 7(} i -„ ^ (5) j _{+ 7(} i -„(5) j + 7( i - 1) + 1

( i = 2197,-••,2214,2295,---,2312,2393,---,2401, j = 1,-,4) and

(5)i (6)7i ^ (6)7i (6)7i+1(i = j + 7(k - 1), k = 2197,-,2214,2295,-,2312,2393,-,2401, j = 1,---,4)

we can get | v (1) - v (0)| = | v - 2 v (0)| = {1007,1005,-• ,649}

Step10: (4) i (5) j ₊ 7₍ i-^ ^ (5) j + 7( i - 1) ⁽⁵⁾ j + 7( i - 1) + 1

( i = 2168 + 7 n + m , n = 2 l ,0 <  l <  1,4 <  l <  8,11 <  l <  15, m = 1,---4, j = 1,-4)

and

(5)i (6)7i ^ (6)7i (6)7i+1(i = j + 7(k -1), k = 2168 + 7n + m,n = 2l,0

and (5)i (6)7i ^ (6)7i (6)7i+1(i = j + 7(k -1), k = 2159 + 21,0 < l< 4,7 < l< 11,14 < l< 18,21 < l< 25, 28 < l< 32,35 < l< 39,42 < l< 46,49 < l< 51, j = 2,3) , we can get |v(1) -v(0)| = |v-2v(0)| = {263,261,- • -,133} Step12: (4)i(5)j₊7₍i_₀^(5)j+7(i^(5)j+7(i-1)+1 (i = 2160 + 21,0 < l< 4,7 < l< 11,14 < l< 18,21 < l< 25, 28 < l< 32,35 < l< 39,42 < l< 46,49 < l< 51, j = -1,0)

and (5)i (6)7i ^ (6)7i (6)7i+1(i = j + 7k, k = 2160 + 21,0 < l< 4,7 < l< 11,14 < l< 18,21 < l< 25, 2 8 < l< 32,3 5 < l< 39,42 < l< 46,49 < l< 51, j = 0,1) , we can get |v(1) - v(0)| = |v - 2v(0)| = {131,129,- • -,1}

Even index set structures as follows:

Step1: (2)4(3)24 ^ (3)24(3)25, we can get |v(1) - v(0)| = |v - 2v(0)| = 15872

Step2: (4)i (5)j+7(i-_n^ (5)j+7(i-_D(5)j+₇₍i-1)+1

(i = 1,---,163, j = 1,---,4)

(5)i(6)7i ^ (6)7i(6)7i₊1

(i = j + 7(k-1),k = 1,---,163,j = 2,---5)  , we can get

I v (1) - v (0)| = |v - 2v (0)| = {15870,15868,---,14568}

Step3:  (4)i(5)j+7(,._„ ^(5),₊7(i_1)(5)j₊7(i_„+1

(i = 230,---,261, j = 1,---,4)

and

(5), (6)7, ^ (6)7, (6)7,+1

(i = j + 7(k-1),k = 230,---,261,j = 2,---5)  , we can get

I v (1) - v (0)| = I v - 2v (0)| = {14566,14564,- • • ,14312}

Step4: (4)i (5)j+7(i-„ ^ (5)j₊₇₍i-„(5)j+_7<i__n+1

(i = 328,-,343, j = 1,---,4)

(5)i (6)7i ^ (6)7i (6)7i+1

(i = j + 7(k-1),k = 328,---,343,j = 2,-5)  , we can get

I v (1) - v (0)| = |v - 2v (0)| = {14310,14308,- • -,14184}

Step5: (4)i(5)j+7(i-₀ ^(5)j+7(i^(5)j+7(i-_D+1

(i = 173 + 7n + m,n = 2l,0 < l< 3,7 < l< 10,m = 1,- • -4, j = 1,-4) and

(5)i (6)7i ^ (6)7i (6)7i+1(i = j + 7(k -1), k = 173 + 7n + m,n = 2l,0

Step6: (4)i (5)j+7(i-₀^ (5)j+7(i^(5)j+7(i-_D+1

(i = 164 + 2lor262 + 2l,0 < l< 4,7 < l< 11,14 < l< 18,21 < l< 25, 28 < l< 32, j = 1,2) and

(5)i (6)7i ° (6)₇i (6)7i+i

(i = j + 7(k -1), k = 164 + 2lor262 + 2l,0 < l< 4,7 < l< 11,

14 < l< 18,21 < l< 25,28 < l< 32, j = 2,3) , we can get I v (1) - v (0)| = |v - 2v (0)| = {13926,13924,-•-,13728}

Step7: (4)i(5)j₊₇₍i-1) ° (5)j_+7(t-,/5)j₊₇₍i-1)+1

(i = 165 + 2lor263 + 2l,0 < l< 4,7 < l< 11,14 < l< 18,21 < l< 25, 28 < l< 32, j = -1,0)

(5)_/(6)_7/ ° (6)7i(6)7i + 1

(i = j + 7k, k = 165 + 2lor263 + 2l,0 < l< 4,7 < l< 11, 14 < l< 18,21 < l< 25,28 < l< 32, j = 0,1) , we can get | v (1) - v (0)| = |v - 2v (0)| = {13726,13724,-•-,13528}

Step8: Similar to the first, second, third, fourth, fifth, sixth step transformation, we can obtain these labeled graphs of edge-balance indexes which are {13526,13524,  ,1808}

Step9: (4),(5)j₊₇₍i_„ ° (5)j+₇(i-1/5)j^i,»+1

(i = 2059,-,2158, j = 1,-,4)

and

(5)/(6)₇i ° (6)7i-(6)7i-+1

(i = j + 7(k -1),k = 2059,-,2158,j = 2,-5) , we can get | v (1) - v (0)| = |v - 2v (0)| = {1806,1804,- ■ -,1008}

Step¹⁰: (4),(5)j₊7₍i_₀ °(5)j₊₇(i_₀(5)j₊₇(,__o+1

(i = 2197,-••,2214,2295,-••,2312,2393,---,2401, j = 1,—,4) and

(5)i (6)7i ° (6)7i (6)7i+1(i = j + 7(k - 1), k = 2197, ••• ,2214,2295, •••, 2312,2393, ••■, 2401, j = 1, • • •, 4)

we can get |v(1) - v(0)| = |v - 2v(0)| = {1006,1004,---,648}

Step¹¹: (4),(5)j^i,» ° (5)j+_7(t-1/5)j₊₇₍i-„+1

(i = 2168 + 7n + m,n = 2l,0 < l < 1,4 < l < 8,11 < l < 15,m = 1,-4, j = 1,-4) and (5)i(6)7i ° (6)7i(6)7i+1(i = j + 7(k -1), k = 2168 + 7n + m,n = 2l,0

(i = 2159 + 2l,0 < l< 4,7 < l< 11,14 < l< 18,21 < l< 25, 28 < l< 32,35 < l< 39,42 < l< 46,49 < l< 51, j = 1,2) and

(5)i (6)7i ^ (6)7i(6)7i+1(i = j + 7(k -1), k = 2159 + 2l,0 < l< 4,7 < l< 11,14 < l< 18,21 < l< 25, 28 < l< 32,35 < l< 39,42 < l< 46,49 < l< 51, j = 2,3), we can get |v(1) - v(0)| = |v-2v(0)| = {262,260,-•-,132} Step¹³: (4)_z.(5)j₊7(i-_n ^(5)j₊7(i-_r)(5)j+7(i-1)+1

(i = 2160 + 2l,0 < l< 4,7 < l< 11,14 < l< 18,21 < l< 25, 28 < l< 32,35 < l< 39,42 < l< 46,49 < l< 51, j = -1,0) and

(5)i (6)7i ^ (6)7i (6)7i+1 (i = j + 7k, k = 2160 + 2l,0 < l< 4,7 < l< 11,14 < l< 18,21 < l< 25, 28 < l< 32,35 < l< 39,42 < l< 46,49 < l< 51, j = 0,1), we can get |v(1) -v(0)| = |v- 2v(0)| = {130,128,---,0} In       conclusion,       we       can      prove

{15872,15871, ••• ,1,0} о EBI(C^5 xp ) .

Lemma 5 In the graph C_T x p^ , for the fan subgraph H^ of the single point, {322,321,-•-,2,1,0} о EBIH^.

Proof:   In the following proof, we use

(2k -1)r(2k)s о (2k)s(2k)s+1 to present that the edge (2k -1)r(2k)s is from 0-edge into1-edge, at the same time the edge (2k) (2k)   is from 1-edge into 0-edge. Among them, we use (a + 2).(a)7z. о (a)7z (a)7z+1 to present that the edge (a + 2)z (a)7z is from 1-edge into 0-edge, at the same time the edge (a)7z (a)7z+1 is from 0-edge into 1-edge.

First, build an even index set:

Step1: (a)₄(a +1)₂₅о (a + 1)₂₅(a + 1)₂₆, we can get | v(1) - v(0)| = | v - 2v(0)| = 322

Step²: ^{(a + 1)}_z.^(a+2)j+7(i-1) °^(a+2)j+7(i-1)^(a+2)j+7(i-1)+1

(i = 1,---,24, j = 1,---,4)

and

^{(a + 2)}i^(a)7i ° ^(a)7i^(a)7i+1

(i = j + 7(k - 1),k = 1,- - -,24, j = 2,---5) , we can get |v(1) -v(0)| = |v-2v(0)| = {320,318,-•-,130}

Step3: (a + 1)i(a + 2)j+7(i__nо(a + 2)j+7(i__D(a + 2)j+7(i__n+1 (29 < i< 32,39 < i< 42,47 < i< 49, j = 1,- - -,4) and

^{(a + 2)}i^(a)7i ^ ^(a)7i^(a)7i + 1

(i = j + 7(k-1),29 < k < 32,39 < k < 42,47 < k < 49, j = 2,--5)   , we can get |v(1) -v(0)| = |v-2v(0)| = {128,126,-•-,42}

Step⁴: ^{(a + 1)}_z.^(a+2)j+7(i-1) °^(a+2)j+7(i-1)^(a+2)j+7(i-1)+1

(i = 25 + 2l,0 < l< 1,4 < l< 6, j = 1,2)(i = 43, j = 1) and

^{(a + 2)}i^(a)7i     ^(a)7i^(a)7i + 1

(i = j + 7(k-1),k = 25 + 2l,0 < l< 1,4 < l< 6, j = 2,3) , we can get |v(1) - v(0)| = |v - 2v(0)| = {40,38,-•-,20}

Step5: (a + 1)i(a + 2)j+7(i-_D° (a + 2)j+7(i-_D(a + 2)j+7(i-_D+1

(i = 26+2l,0 < l< 1,4 < l< 6, j = -1,0) and (a + 2)_z(a)_7i ° (a)_7i(a)_7i+1 (i = j + 7k, k = 26 + 2l,0 < l< 1,4 < l< 6, j = 0,1) , we can get |v(1) -v(0)| = |v-2v(0)| = {18,16,-•-,2,0}

Odd index set structures as follows:

Step¹: ^{(a +}1⁾i^(a+2)j+7(i-1) °^(a+2)j+7(i-1)^(a+2)j+7(i-1)+1

(i = h- -,24, j = 1,---,4) and (a + 2)i(a)7i ° (a)7i(a)7i+1 (i = j + 7( k - 1), k = 1,---,24, j = 2,---5) , we can get |v(1) -v(0)| = |v-2v(0)| = {321,319,-•-,131}

Step2: (a + 1)i(a+2)j+7(i-_D°(a+2)j+7(i-_D(a+2)j+7(i-_D+1 (29 < i< 32,39 < i< 42,47 < i< 49, j = 1,- - -,4) and

^{(a + 2)}i^(a)7i ° ^(a)7i^(a)7i + 1

(i = j + 7(k-1),29 < k < 32,39 < k < 42,47 < k < 49, j = 2,---5)   , we can get |v(1) -v(0)| = |v- 2v(0)| = {129,127,-•-,43}

Step³: ^{(a + 1)}i^(a+2)j+7(i-1) °^(a+2)j+7(i-1)^(a+2)j+7(i-1)+1

(i = 25 + 2l,0 < l< 1,4 < l< 6, j = 1,2)(i = 43, j = 1) and

^(а + 2) i ^(а)7 i ° ^(а)7 i ^(а)7 i + 1

(i = j + 7(k-1),k = 25 + 2/,0 < l < 1,4 < l < 6, j = 2,3) , we can get |v(1) -v(0)| = |v-2v(0)| = {41,39,- • -,21}

StCp4: ^(a + 1)i^(a + ²⁾j₊7(i—1) ° ^(a + ²⁾j₊7(i—1)^(a + ²⁾j₊7(i—1)+1

(i = 26+2l ,0 < l< 1,4 < l< 6, j = -1,0)

and

^(a + ²⁾i ^(a)7i ° ^(a)7i ^(a)7i+1

(i = j + 7k, k = 26 + 2l,0 < l< 1,4 < l< 6, j = 0,1) , we can get v(1) - v(0)| = v-2v(0)| = {19,17,-•-,3,1}

V. Conclusion

In this paper, in order to study the edge-balanced index sets of the power circle nested graph, we introduced the fan sub-graph of the single point, and showed the proofs of the computational formula, at the same time, we gave the construction of the corresponding graphs.

In conclusion, we can prove {322,321,—,1,0} c EBIH^.

Lemma 6 For the power-cycle nested graph C x P

when m = 2(mod3) and

m > 5

17 - 7^m - 23 17-7^m - 41

18     ^,     18

,-,1,0 ^c EBI (C7 m x Pm).

Proof: In the lemma 3, when m = 2(mod3) m > 5 ,

m

max{EBI(C7„ xPm^)} = —

18

.

Step 1: For the power-cycle nested graph, according to the edge transform method by lemma 5, each of the fan sub-graph H of the single point index can decrease 323, so {322,321,-•-,1,0} c EBIH . In the graph Cm x P (m > 5) , there are 7⁵+ 78 + • ■ • + 7^m"³= 7^-7- the

same fan sub-graph of the single point , the edge transform method of the fan sub-graph of single point is the same as lemma 5, then their index can decrease 7^m - 7⁵      323(7^m - 75)        17 - 7^m - 5 323(7^m - 75),^^ .

--323 =---------- , and---= 15o/j. so 342           342               18         342

7^m - 75 we can

the fan sub-graph of the single point to

conduct edge transform, and we can obtain these labeled graphs of edge-balance indexes which are f17 - 7^m - 23 17 - 7^m -41

,            ,   ,15873

[    18          18

Step 2: At last, we can make the edge transform in the 5 circle foundation figure. The edge transform method of the 5 lap is the same as lemma 4, the index can reduce 15873, so we can obtain these labeled graphs of edgebalance indexes which are {15872,15871,-•-,1,0}.

In       conclusion,       we       can

[17 - 7^m -

I   18"

23 17 - 7^m - 41

,     18

,---,1,0[c EBI (C7 m x Pm₇).

Acknowledgments

This work was financially supported by Applied Mathematics Provincial-level Key Discipline of Henan Province, Operational Research and Cybernetics Key Discipline of Henan Polytechnic University and the Education Department of Henan province science and technology research project (12B110009).