On the solution of the setting quality problem for the relay controllers

Today no one of the complex technological systems or objects can operate being non-automated. Automation provides high quality of the system and object operation as well as a considerable saving in power and material resources. The systems and objects are also known to have a significant number of controlled sections fitted with the positional executive units that can be replaced only under extremely disadvantageous conditions. In this case, even providing that there are modern microprocessor controllers with a large set of regulating algorithms in their libraries, the only possible solution of an automation problem is application of position PID-controllers [1–2]. It should be noted that the technical implement of the discrete outputs for controlling the positional executive units is much more accessible than the analog ones. As a result, the number of the control circuits maintained by a single controller increases substantially while the control system cost reduces as a whole.

The control quality problem

It is well known that the position PID-controllers usually operate in oscillatory mode (two-position controllers can work only in oscillatory regime) which is undesirable in terms of operating quality of the automatic control systems (ACS). The quality of ACS operation should be acceptable as it defines the automation efficiency. The problem is being solved by a choice of a controller settings. However, the approximate graphical or grapho-analytical methods are still used to estimate the dynamic parameters of the objects [3–5], so the problem of the setting calculation for such systems remains actual [6]. The accuracy of analysis and control circuit adjustment performed by using these methods does not meet modern requirements while the labour input is high. Therefore, it is reasonable to apply the direct simulation transient analysis to ACS by using computer. In this case the questions of the desired setting accuracy, complete transient analysis, and reducing the amount of relevant graphical layouts and manual calculations are settled.

Parametric identification of the models of controlled objects

The calculation of the controller settings begins with estimating the dynamic parameters of a control object, so let us consider the problem.

It is common knowledge that the dynamic properties of a great number of control objects can be presented by the following types of differential equations:

Управление в технических системах

a 1 dx ( t ) / dt + x ( t ) = kU ( t - t ) ;                                                                        (1)

a 2 d ² x(t ) / dt ² + a 1 dx ( t ) / dt + x(t ) = kU (t - t ) ,                                                        (2)

where x(t ) is a controlled coordinate, U is a control action, t is time, t is delay time, k is the transition factor of an object, a ₁ and a ₂ are the coefficients of the differential equations.

It is found that the differential equations describe the dynamic properties of specific objects with a desired accuracy only if the coefficients a 1 , a ₂, and k as well as the delay time t are determined satisfactorily (it is evident that for the model (1) there is no coefficient a ₂ ). Let us consider a solution of the problem.

Suppose that an experimental transient response curve of a control object is known. Let us regard the information specified by the curve and the structure of the models (1) and (2) as initial data for solving an identification problem. An experimental response of the object to any input action U can be basically used instead of the experimental transient response curve. Let us formulate the identification problem as follows. It is required to find the values of the coefficients a 1 , a ₂, k and the delay time t such that the identification criterion

n

I ^{( k} , a 1 , a 2 , ^{t )} = ^ ^[ x E ⁽ t i ) ^- x ⁽ t i )] 2

i = 1

has a minimal value. Here xE is an experimental value of the object output, x is a calculated value which is determined from the model of the object (1) or (2) for equal input action U , ti are the time moments used for identification, n is a number of experimental points.

Cauchy form. To provide the desired calculation accuracy, the program is developed in such a way that each time interval between two experimental points contains an integer number of the calculated steps.

The developed identification procedure was tested for a large set of the experimental transient re- sponse curves given in [4–5]. In each case the identification results had an adequate quality level. For example, Fig. 1 shows both an experimental transient curve and the curve calculated by the adjusted differential equation, for the water-water heater through the “delivery water flow rate – temperature of the water leaving a heater” channel. The experimental curve is full and the calculated one is dashed.

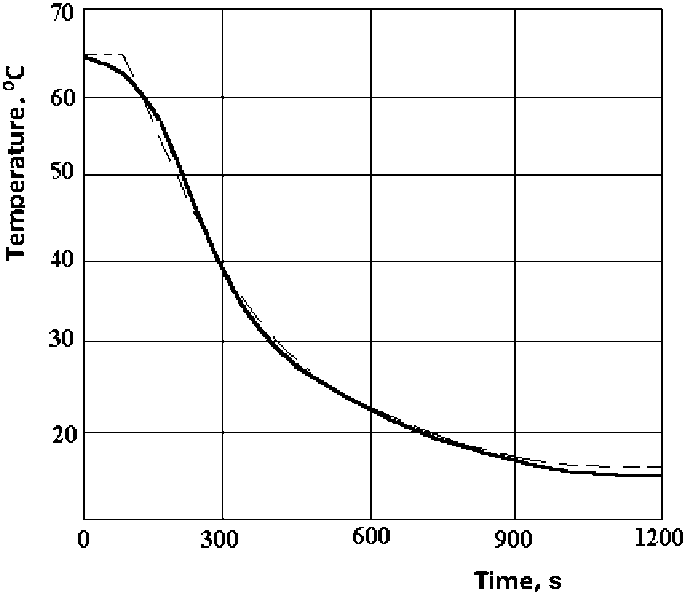
Fig. 1. Experimental and calculated transient curves for a water-water heater

The heater with 108 mm body outside diameter had 6 series-connected sections each of which was 4 m in length. The heater entry temperatures of the delivery water and the water to be heated were 69 and 14 °C relatively. The flow rate of the water being heated was supported as a constant equal to 0.664 kg/s while the delivery water flow was decreased from 1.14 kg/s to 0 kg/s. In this case, the control object was described by a differential equation of a second type with the determined parameter values as follows:

• a 1 = 256 s; a ₂ = 999 s² ; t ob = 62 s ;

k_ob = 43.85 °C/(kg/s).

Here the mean-square deviation of the calculated curve from the experimental one I / n is equal to 0.42 °С, that is wholly satisfactory.

The identification procedures for the dynamic properties of the control objects were developed from the transfer function of the operating ACS [7]. The necessity can be explained a follows.

The dynamic properties of the control objects are known to vary significantly when the operation mode is changed [7]. The greatest variation usually happens to the object’s transition factor which numeric value can change by several times while in operation. The variability of the object’s dynamic parameters results in the changes of regulation quality values in the systems with constant settings of the automated controllers when the operation mode varies. The attempts to define and apply the causeeffect relations for monitoring the dynamic parameter values in order to improve the regulation quality cannot solve the problem as a whole because of strong instability of interrelations [7]. In the circumstances, it seems appropriate to determine the dynamic parameters of the control channels and optimize the settings of the automatic controllers in the process of the furnaces operation. Thus, the dynamic properties of the control objects need to be determined while ACS works according to its response on the step input of the closed-loop transfer function [7–9]. At that, either the assigned disturbance or disturbance by regulating unit (load disturbance) is applied. The latest action can be organized by issuing the command of transferring the control loop to the manual control mode through the interface connection channel followed with a quick change of regulating unit position and immediate return to the automatic mode. It is clear that the mathematical model of the whole control loop is to be used in the case. It should be noted that the developed identification algorithms can be easily modified for a case when it is necessary to minimize a sum of the magnitudes of the differences between the calculated and experimental values of x coordinate instead of the criterion (3). It can also be modified for the case of a minimax problem which requires to minimize the maximum deviation of the calculated values from the experimental ones. The criterion (3) is preferable considering that the parameter estimations obtained by minimizing the criterion are most credible. Besides, the use of integral identification criteria requires minor changes in the programs.

Simulation of relay ACS

While simulating, it was considered that two-position PID-controller forms control action as follows:

^U min , if ^e<^e res ^{-A ;}

U i =VU max , if S^e res ;

U i — 1 ,if e _res -A_res.

Here e is an actuating signal calculated by a standard system comparison component, that is, by a formula e(t) = xsv (t) - x(t), where xsv (t) is a set value of the adjustable technological parameter, eres is a response value of PID-controller, A is a width of a hysteresis loop, Umin and Umax are minimum and maximum of control action values, respectively, i is a number of a calculated time step.

The response value e _res and the width of a hysteresis loop A are viewed as the setting parameters of two-position PID-controller.

An operation algorithm of three-position controller is as follows.

^U min , ^{if e-e} 0 ;

U i - 1^{,if e} 0 <^e< ^{( e} 0 +^A 0 );

U i =1

U ave ,if( e 0 +A 0 ) ( S i -A 1 );

U - 1^{,if ( e} 1 ^-A 1 ) <^s<^s i ;

^U max^{,if e}^^e 1 .

Static characteristic of three-position controller with a description of the added designations is given in Fig. 2. The transient analysis of two-position ACS for an object with the dynamic properties presented in Fig. 2 demonstrated that, for example, when xsv(t) = 60°C, Umin = 0kg/s, Umax = 2kg/s, eres = 1 °C, A = 2 °C the positive amplitude length (the length of time span where Ui = Umax) was equal to 181 s, and the negative amplitude length (the length of time span where Ui = Umin ) was equal to 99 s.

Управление в технических системах

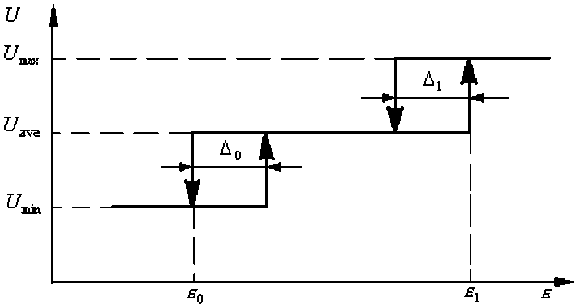
Fig. 2. Static characteristic of three-position controller

The positive amplitude of the controlled value deviation from the preset value was 6.8 °С in the case while the negative one was 14.0 °С. The controlled value average was equal to 56.4 °С meaning that there was a sustained deviation of the controlled value average from the preset value. To remove the error, the settings for the controller were corrected.

Decrease of the two-position controller settings s res and A to 0 °C resulted in slight changes of the values of the control quality level. The length of the positive amplitude decreased to 170 s while the negative one came to 90 s. At that, the positive amplitude of the controlled value deviation from the preset value was equal to 5.9 °С while the negative one was 13.1 °С.

The presented values of the control quality level are strongly due to the high value of the control object delay time т . So, the transient analysis for the same conditions as those in the first case but at т = 0 s showed that the length of the positive amplitude decreased to 30 s while the negative one came to

• 15 s. At that, the positive amplitude of the controlled value deviation from the preset value was equal to 1.1 °С while the negative one was only 1.3 °С.

The simulation also showed that the method of partial inflow (when Umin + 0 because of applying bypass) under two-position control allows achieving acceptable control quality in each case. For exam- ple, when xsv (t) = 60 °C, Umin =1kg/s, Umax = 2kg/s, s res =1°C, A = 2 °C the length of the positive amplitude was only 105 s and the length of the negative amplitude achieved 170 s. In this case, the positive amplitude of the controlled value deviation from the preset value was equal to 6.8 °С and the negative

Temperature, °C

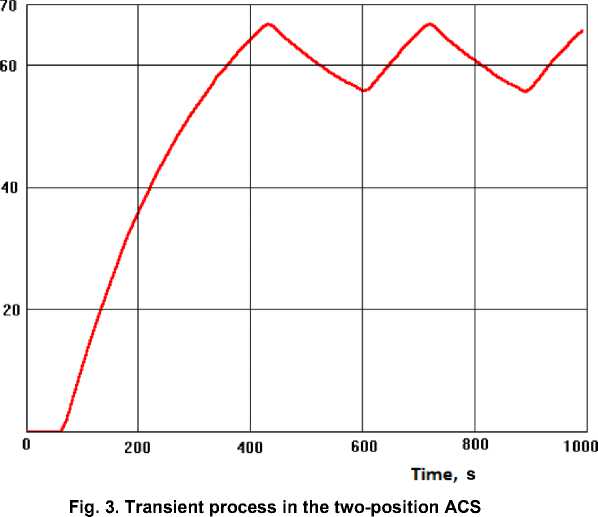
one became 4.3 °С. The controlled value average was equal to 61.3 °С. Thus the control quality was noticeably improved. The transient process specific to this case is demonstrated in Fig. 3. The ways to improve the control quality in two-position ACS are presented in the papers [10–14].

The advantages of the three-position control are well-known [1–3]. Firstly, it is a possibility to obtain a non-oscillatory transient process and secondly, all things being equal, it is a lower value of both amplitude and frequency of the self-sustained oscillations. In Fig. 4 there is a graph of the non-oscillatory transient process under the three- position temperature control in a hot water system with a heater which dynamic properties are presented in Fig. 1. This transient process was achieved under the following settings of the controller:

x sv ( t ) = 60 °C, U min = 0kg/s,

U ve = 1.36 kg/s, U_m ax = 2kg/s,

8 1 = 5°C, A 1 = 0,5°C,

• 8 0 =- 5 °C, A 0 = 0,5 °C.

Consequently, the using of the three-position controllers in the automatic control systems is more preferable.

Conclusion

The parametric identification procedure for the dynamic properties of the control objects, and

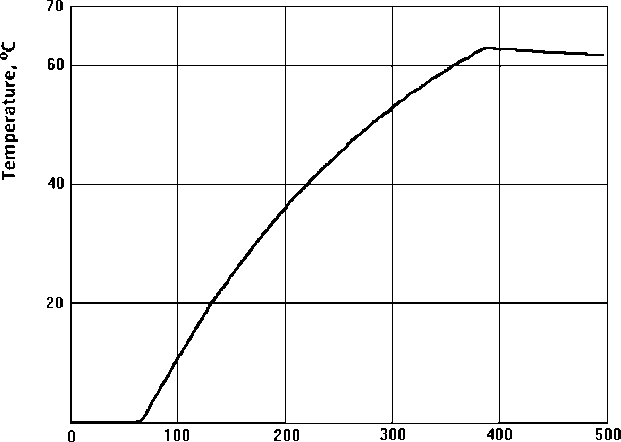
Time, s

Fig. 4. Transient process in the three-position ACS

the computational models of the two-position and three-position automatic control systems have been developed. The developed models are recommended for analyzing a system setting quality and choosing the parameters of the controller settings.