On the theory of spaces of generalized bessel potentials

We consider the Cauchy problem for degenerate parabolic equations in the form

p(|x|)ut(x,t) = Am,pu(x,t), (x, t) G St = RN x (0,T), N > 1,          (1.1)

u(x, 0) = uo(x) > 0, a. e. for x G RN.                        (1.2)

Here

A^*' := E dxi (um-1 |Vu|p-2 ^) .

i =1

We assume that p > 1 and p+m — 3 > 0 that is (1.1) is of the slow diffusion type. Additionaly, we assume that p < N. The function p(s) is assumed to be positive nonincreasing, continuous function in [0, to), satisfying the condition p(0) = 1, and

(0 2022 Dzagoeva, L. F. and Tedeev, A. F.

H i : there exists a positive constant l: l < p, such that the function s l p(s) is nonincreasing for all s E (1, to ) ,

H 2 : there exists a positive constant a < p, such that the function s ^a p(s) is nondecreasing for all s E (1, to ) .

Note that H i and H imply that there exists y > 1 independent of s, such that Y ^{- 1} s ^{- a} C p(s) C Ys-¹ for all s E (1, to ) .

The qualitative theory of degenerate parabolic equations with variable coefficients and, in particular, with inhomogeneous density has attracted much attention. This is explained by the fact that the asymptotic properties of solutions essentially depend on the nature of the behavior of the coefficients at infinity. In particular, the typical properties of degenerate equations with constant coefficients, such as the compactness of the support, the behavior at large values of time may not take place depending on the degree of degeneracy of the inhomogeneous density at infinity. Firstly the surprising properties of solutions for degenerate parabolic equations with inhomogeneous density were established in [1]. Namely, in one dimensional Cauchy problem for the general porous media equation (PME) with inhomogeneous density, provided the density decays fast enough the solution of the corresponding Cauchy problem tends to the constant as t ^ to . The latter means that the solution of the mentioned Cauchy problem as t ^ to behaves as a solution of the corresponding Neumann problem in a bounded domain. The paper [2] is devoted to the asymptotic behaviour of solutions to the Cauchy problem for inhomogeneous PME for slowly decaying density. These results were extended and developed in [3–7]. Another nonstandard property of degenerate parabolic equation with inhomogeneous density is the possible absence of the finite speed of propagation globally in time see [8]. Results of [8] were generalized in [9, 10] (see also [11]), where in particular, new critical exponents have been found for a doubly degenerate parabolic equations with inhomogeneous density. The paper [12] was devoted to the studying of large time behavior for degenerate Neumann problem in domains with noncompact boundaries. We recommend to the reader interested the qualitative theory of degenerate parabolic equations the survey [13]

The goal of the paper is to obtain the precise rate of stabilization of ||u(t) ||_ro r n as t ^ to . To this end we need the precise form of the nonpower weighted Sobolev–Gagliardo–Nirenberg which is of independent interest. Here we note that the classical weighted Caffarelli–Kohn– Nirenberg inequality [14] deals with the power-like weights.

Let us start with definition of the weak solution of (1.1), (1.2).

Definition 1.1. By a weak solution of problem (1.1), (1.2) in S T we mean a non-negative measurable function u(x,t) such that for a = (p — 1)/(p + m — 2), and any t >  0, u(x,t) ^{1 /a} belongs to the class L _p ((t, T ) x W p ( R N )) П C ([t, T ]; L \.^,_p ( R N )) and (1.1), (1.2) is satisfied in the distributional sense. Moreover, pu (^ t) ^ pu g as t ^ 0 in L i ( R N ). Here, by Wp( R N ) and L     ( R N ) we denote the Sobolev space and weighted Lebesgue integral correspondingly.

Before formulating results of the paper, we define

w(s) := p(s)s p , ^ p,a (s) := w(s)s “-* ^{( p - a )} .                         (1.3)

Let also

E q,p ^{( f} ) ^: = j P ^{( | x | ) | f (x) |} q ^dx

R ^N

and

D p (f) := j M (x) l p dx.

R ^N

Our first result reads as follows.

Theorem 1.1. Let Dp(f), Ea,p(f) < to, where 0 < q ^ p and 0 < a < q, then we have q-a

E q,p (f ) <  C(N,p) (D p (f)) p - a

X

J, ( - 1)(^ . v v(Dp (f )) ^p

q-a p-a             p-q

))     ( ^Ea , ,(f )) --,

(1.4)

where ^ ^{( - 1)} is inverse function to ^.

The optimal decay rate is given by the following theorem.

Theorem 1.2. Let u(x, t) be a weak solution of (1.1), (1.2). Assume that HpuoIIl^rn) < to, then there exists globaly in time solution u(x, t) in S^ and for any t > 0 the following estimate holds true u t      (RN) < Yt-■

^X [ ^Ш ( ^Ф 1 ^{- 1)} ((^|u(t)^| - i ( _R N ₎ ^{| u} 0 P^| 1 , R N ) NN ))] ^{P + m}- ³ •                    ^(L5)

Remark 1.1. Note that if p(s) = (1 + | x | ) ^a , then (1.5) implies that (see [10])

p - α                   _N-α

Ht) H l_ ( r n ) <  Y •      ' „ • ^P "    '   ' t N ^P .

Remark 1.2. If а = 0 and m = 1, then the latter coincides with the classical result (see, for example, [15]).

In the proof of Theorem 1.2. we use the classical De Giorgi–Ladyzhenskaya–Uraltseva– Di Benedetto approach in the form of [16, 17]. The rest of the paper is organized as follows. In the Chapter 2 we prove Theorems 1.1 and 1.2. In what follows, we use the symbols 7 > 0, b > 1 for the constants depending on the parameters of the problem, p, m, N only and which may vary from line to line. Moreover, for simplicity we will understand the equation almost everywhere.

2.    Proofs of Theorems 1.1 and 1.2

Proof of Theorem 1.1.

E q,p (f ):= / I f I q p( I x I ) dx, D p (f ):= j \f | ^p dx. R ^N                    R ^N

.,(,)= /„«- .. . / ............ B r                R ^N \ B r

(2.1)

By the H¨older inequality, we get j I f Iqp(IxI) dx <

R ^N \ B r

f

R ^N

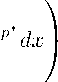
p∗ -a p∗

p ^∗ - a

I f I a p( I x I ) ^p*-^q dx

R ^N \ B r

Np

N — p

1 -

q - a p ^∗ - a

,

(2.2)

Making use the S. L. Sobolev inequality:

p ∗                                 ₁

| f | ^p * dx I     ^ (S(N,p)D p (f)) ¹ ,

RN where S(N, p) is the sharp constant in this inequality, and owing to the monotonicity of p:

[ I / IMI x l )

R ^N \ B r

p -a             p^-a

p*-q dx ^ p(r)qEaappff), we get from (2.2) that p q-a        q-a            p∗ -q

(2.3)

| f | ^q p( | x | ) dx ^ (SD p (f )) ^{p p}*^-a p(r) ^p*^-a E _a , p (f ) ^p*^-a .

R ^N \ B r

Next, using the classical Hardy inequality j If|p|xrp dx < (N-p)pDp(f),

RN and the H¨older inequality, we obtain q-a p-a j If |p |x|_p dxl

R ^N

q - a

| f | ^a | x | ^p p - q

B r

p - a

ρ | x | ^{p - q} dx

p - q p - a

(2.4)

q - a            q - a             p - q

^ C(N,p) (D p (f )) pa (r p p(r)) pa (E_a p (f )) p-a .

Combining now (2.1), (2.3) and (2.4), we get p∗ q-a        q-a            p∗ -q

Eq,p(f) ^ (SDff)) p p*-a p(r) p*-a Ea,p(f) p*-a q-a            q-a             p-q

+ C(N,p) (D p (f )) p - a (r p p(r)) p - a (E_a p (f )) p - a .

Finally, choosing the free parameter r from the relation:

p ^∗ q - a        q - a           p ^∗ - q                           q - a             q - a              p - q

(SDp(f)) p p*-a p(r) p*-a Ea,p (f) p*-a = C (N,p)(Dp(f))p-a (rpp(r))p-a (Eap(f))p-a , we have q-a q-a

E q,p (f ) <  C 1 (N,P) (D p (f)) p^-a

“(^{P < _ 1)}(7E a, ^P (f^ ^Ip — a ( E ap (f )) “■

- V     V (D p (f )) p^¹

If q = P, we get from the last inequality:

E p,p (f ) <  C 1 (N,P) D p (f)

ω

(^^{( _ 1)} (

E a,p (f ) (D p (f)) p

))

The proof of (1.4 ) is similar. We give the sketch of the proof only. We have for any R fixed. Applying the H¨older, Hardy and Sobolev inequalities, we obtain

Ep,p(f ) = j |f \ppdx + У |f \ppdx ^ p(R)Rp J |f |p |x|-pdx BR         RN \BR                RN p-a

+ p p^-a

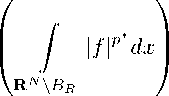
p - a p ^∗ - a

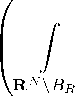
p ^∗- p p ^∗ - a

| f | a pdx I

/ p \ P                        p — a        pKp-a)          P*-P

^ (N—p) P(R) RpDp(f) + S1 pDp(f)P(P*-a) Ea,p(f), where Si = S(N^pY*^ a)/(p* a). Let us choose R from the equality

p(p*-a)                        a

Rp(R) = Dp(f)—"P Ea,p(f), that is

(N—p)(p — a)                 a

^(R) := ^(R)R     ^p = D p (f ) ^{— P}p E a,p (f).

Therefore,

E p,p (f ) <  ' -J <    (EaTf))) D p (f ).

V     V D p (f )^p//

Theorem 1.1 is proved. >

We need the following Caccioppoli type inequality.

Lemma 2.1. Let 9 > 0, and 9 >  2 — m if m <  1 , be fixed, and define s = (p + m + 9 — 2)/p . Fix also a i > a 2 > 0, T i > T 2 > 0, Г 2 > r i . Then

/ Г Г                            /          \ |m— 1 1

(u(r) — a ₁ ) +⁺¹ p( | x | ) dx + J J | V (u — a ₁ ) + | ^P dxdT <  y( ----¹— J

B r1

^{T 1} B r 1

x MT 1 — T 2 ) ¹ j j (u — a 2 ) +⁺¹ p( | x | ) dxdT + (r 2 —

^{4              T}1 B r ₂

_t                                  (2.5)

r 1 ) ^{— p} j   J (u — a ₂ ) Sp dxdTj .

T 1 B r ₂ \ B r1                     '

For the proof of (2.5) we refer the reader to [16]. Passing Г2 ^ to, ri ^ to in (2.5), we arrive at

t sup / (u(t) — ai)++ip(|x|) dx + / / |V(u — ai)+|P dxdT Ti

RN                        T1 RN

(2.6)

/           \ |m—1|                  t p

^ Y( _a1 —1 a₂ )      (Ti — T2)^— у J (u — a2)+⁺¹p(|x|) dxdT.

T2 RN

Proof of Theorem 1.2.

< Define for ho > h^ > 0, tq > t^ > 0, and i = 0,1, 2,... , ki — h^ + (h0  h^)2 , ti — T^ + (t0  t^)2

p+m+9 — 2

fi = (u — ki )7^”

Now using the Holder inequality and the embedding (1.4) with f = fi and q = p(1 + 9^/(p + m + 9 — 2), a = p/(p + m + 9 — 2) we obtain that

q

p

2ⁱ                                          2ⁱ                                                  q

Y-(---------7    fiP^(|x|) ^dx< 7 7---------7        fi P^(|x|) ^dx    Ji^(T) ^p

^(To ^{— T}ro) J                    ^(To ^{— T}ro) \                  /

RN                      RN iq                                             q

< CiY (_{To — T} ) (Dp^(fi))^p[^ш(^ф1^-1)(ciJi^(T)^ТУ) p Ji^(T)L

q p

(2.7)

p

^ a^qDp(fi) + 7a

p p-q ) CiY

2i

(To — Tro)

qp

[^ш(^ф1^-1)(ciщ^(т)N}}] p щ^(т)1-p I

.

Here it is denoted

Ji(t) := j p(|x|) dx.

u(t)>ki

Integrating in time (2.7) and denoting Mi(t) = supo<_T<_tji(T) we get

Y (_To—i_T„) У^Г / fi+iPdxDdx< e J^f/|V/-+iipdxdT ^∞ti+1 R^N                  ti+1 R^N

-^p             -^p

+ 7E ^p-qt(To — Tro) ^p-q I

ho ho ^— hro

)

p|m-1| p-q

q x [ш (ф1-1) (cMi+i(t)N^j p-q Mi+i(t).

Combining now (2.8) and (2.6) with ai = ki, a2 = ki+i, Ti = ti, T2 = ti+i, we get

(2.8)

t

Ji := sup [ fiqp(\x[) dx + У [ |Vf_i|^pdxdT ti <τ

R^N

^ti R^N

t

^ e j I |Vfi+i|p dxdT ti+1 RN

-^p             -^p

+ Ybie ^p-qt(T_o— T_ro) ^p-q I

ho ho ^—hro

p|m-1| p-q

q x ^ш (ф!-1) (cMi+i(t)N^j p-q Mi+i(t).

Iterating this inequality, we get

p|m-1|

•              p                    p / ho      I p-q

Jo < Ei Ji + ye-p-q t(To — Tro)-p-q 7---- ho — hro qi x [ш (ф1-1) (cMro(t)^))] p-q Mro(t) ^(be).

k=0

Choosing e so small that eb < 1 and letting i ^ to, we have

sup     foP(|x|) dx< 7t(To — Tro) p'-q (

τ0 <τ

R^N

ho ho ^— hro

p|m-1| p-q

х [_Ш(ф1^-1)(cM^(t)n))] p-q M^(t).                       (2.9)

To complete the proof, we need the second iteration. Let k > 0, n = 0,1, 2,... , and

Kn = k(1 - 2^-n-1), Kn = Kn +₂Kⁿ⁺¹, tn = t(1 - 2^-n-1).

Applying (2.9) with tq = tn+₁, t^ = tn, ho = K_n, h^ = Kn, we deduce from (2.9) that

Y_n+1 := sup f    p(|x|) dx C Ybnk ⁽¹⁺⁶⁾

tⁿ⁺¹<^T(T)>Kn₊₁

х sup j    (u - Kn)'"p(|x|) dx

(2.10)

tn⁺¹<^T)>Kn+1

C Ybⁿk^-(1+6)t^-p—qq P^1^-1)(cYn^))] p-qYn, b> 1.

Taking into account the property H1 and H2, which imply that ф1 ¹⁾(sA) C A^{N/(N 1)}ф1 ¹⁾(s) for 0 < A C 1, ф1 ¹⁾(sA) C ф1 ¹⁾(s) for A > 1, and Yn C Yq, we derive from (2.10) that

Y <-b n fc^-(1+6)t^-p+^-s [_Ш((Ь ^(-1)(y Ni ^^] ^p+m-3Y^-a y^1+aa—_____N(¹+^)_____ Yn^{+1 C Y}b k t ^p     |_^^ф1 ^₀           ^Yq Yn , a =(n — i)(p + m — ₃).

Thus the last inequality has a form

Yn+1 C bn CY ⁺ .

C = Yk^-(1+6)t^-p+m^- ^'⁽Ф⁽ ' (Yf ))^{] p+m-}3 Y₀^-a, e = a.

Then, using the iterative lemma (see [18, Chap. 2, Lemma 5.6]), we conclude that Yn ^ 0 as n ^ to, provided YqC^1/eC b^-1/e , that is

k

11—p+m-3 ^[_ш(ф1^-1)^YNN))^]p+m^-c 6,

(2.11)

where 5 is a sufficiently small constant depending on the data of the problem. Thus u C k. Next, note that by the Chebyshev inequality we have

Yq C sup I p(|x|) dx Cy sup I u(x,T) p(|x|) dx Ct [ uo p(|x|) dx, 0J              k 0J                      kJ

u(t)>k                       u(t)>k                         RN where we also have used the estimate ||u(t)p^1 rn C huoPh1 rn (see [10]). Thus, it is enough to check that k-1 t-p+m1 -3 [ш(ф1-1)((k-1|uop|1,RN)1/N))] p+m-3 C 5.

To this end, we can choose the free parameter k as follows k = 5r p+m—5 [ш(ф1-1)((к-1|иор|1Л„ )1/N))]p+m-3

Then, after taking into account that |u(t)|^ C k and using the monotonicity arguments, we arrive at the desired result. Theorem 1.2 is proved. >