On the Use of Rough Set Theory for Mining Periodic Frequent Patterns

Published Online July 2016 in MECS

Data mining refers to extracting useful and valuable information from the huge amount of data [1]. By performing information mining, interesting learning, reliabilities, or high-level data can be removed from the database and viewed or browsed from diverse methodologies. The discovered learning can be connected to choice making, procedure control, data administration, and query handling. Information mining is viewed as a standout amongst the most imperative wildernesses in database frameworks and one of the promising interdisciplinary advancements in the data business. Information mining, with its guarantee to productively find profitable, non-clear data from expansive databases [2], is especially powerless to abuse. So, there may be a variance between information mining and protection. Quick advances in information gathering and storage innovation have enabled the association to collect inconceivable measures of information. It has been assessed that the amount of information on the planet copies every 20 months and the size and number of the databases are expanding considerably quicker. However, extracting helpful data has demonstrated greatly difficult. Conventional investigation devices and strategies can't be utilized due to the massive size of information [3]. The field of data mining is vast and consists of various subfields which are available in the literature. By using data mining, we can discover the patterns of data. There are data mining teams working in business, government, financial services, biology, medicine, risk and intelligence, science, and engineering. Whenever we collect data, data mining is applied and providing new knowledge into human endeavor.

One of the major growing fields is the frequent pattern mining in association rule mining which has been explained in detail further.

• A. Association Rule Mining

Association rule mining is a well-known method to discover interesting rules and relations between various items in large databases. Based on the concept of strong rules, Rakesh Agrawal et al.[4] introduced association rules for finding regularities between items in large-scale exchange information recorded. An association rule has two different sections, an antecedent (if) and also a consequent (then). An antecedent is a created item in the knowledge. A consequence is a found item combination with the antecedent.

Association rules are complete through examining data for frequent patterns if/then and using the support and confidence function to identify the most important relationships. Support shows that frequent items show up how many times in a database. Support(s) of an association rule is defined as the percentage/fraction of records that contain X ∪ Y to the total number of records in the database. The count is increased when item is different transaction T in database D during the scanning process. It means support count doesn’t take into consideration quantity of the item into account. Confidence demonstrates the times quantity the if/then statements discovered to be valid [14]. Confidence of an association rule is defined as the percentage/fraction of the number of transactions that contain X ∪ Y to the total number of records that contain X, where if the percentage exceeds the threshold of confidence an interesting association rule X→Y can be generated.

Association rule generation is generally divided into two step process.

• •    A minimum support threshold is applied to find all frequent item-sets in a database.

• •    A minimum confidence constraint is applied to these frequent item-sets in order to form rules.

3-itemsets list as present in Table 1(e). Each those processes are performed iteratively to find each frequent itemsets until the candidates itemsets or the frequent itemsets become empty. The outcome is the same as the algorithm of AIS.

ст( X uY )

Support ( X ^ Y ) =   ^—- .        (1)

Confidence ( X ^ Y ) =

<Г ( X u Y )

^( X )  .

Numerous business enterprises collect vast amounts of information from their regular operations. For example, large quantities of client purchase information are gathered day by day at the grocery store checkout counters. Association rule mining can be of many forms and various other fields can be easily merged in this.

Association rule mining depends mainly upon finding the frequent itemsets. For finding the frequent itemset we use Apriori algorithm as one of the most important algorithm to find the frequent itemset.

B. Apriori Algorithm

Apriori algorithm was first given by Agrawal in[Agrawal and Srikant 1994]. Apriori is the improvement over association rule mining. The AIS is straightforward method that requires many passes over database, generate several candidate itemsets and store counters of each candidate while most of them turn out to be not frequent. Apriori algorithm is good for candidate generation process. Apriori employs a different candidates generation method and a new pruning technique.

There are two different procedures to find out all huge itemsets from Apriori algorithm database. First the candidate itemsets are created, then scanned database to check the actual support count of the corresponding itemsets. At the time of first scanning of the database the support count of all item is designed and large 1 -itemsets are created through pruning those itemsets whose supports are below pre-defined threshold as present in Table 1 (a) and (b). In all pass only those candidate itemsets that conclude the similar specified number of items are created and also checked. The candidate k-itemsets are created after (Q-1)th passes over the database through joining frequent Q-1 -itemsets. Each the candidate Q-itemsets are pruned through check their sub (Q-1)-itemsets, if any of its sub (Q-1)-itemsets is not in the list of frequent (Q-1)-itemsets, this Q-itemsets candidate is pruned out because it has no hope to be frequent according Apriori property. The Apriori property says that each sub (Q-1)-itemsets of the frequent k-itemsets must be frequent. Let us consider the candidate 3-itemsets generation as an example. First each candidate itemsets are created through joining frequent 2-itemsets, which include (A1, A2, A5), (A1, A2, A3), (A2, A3, A5), (A1, A3, A5). Such itemsets are then checked for their sub itemsets, since (A3, A5) is not frequent 2-itemsets, the last two 3-itemsets are eliminated from the candidate

Table 1. Apriori Mining Process

Item	Count No.
A 1 A 2 A 3 A 4 A 5 A 6	7 8 6 2 3 1

Items	Count No.
A 1 ,A 2 A 1 , A 3 A 1 , A 5 A 2 , A 3 A 2 , A 5 A 3 , A 5	5 4 3 4 3 1

Large 1 Item

A 1

A 2

A 3

A 5

(a) C 1                                     (b) L 1

Large 2 Items

A 1 , A 2

A 1 , A 5

A 2 , A 5

A 2 , A 3

A 1 , A 3

(c) C 2                                        (d) L 2

Items	Count number
A 1 ,A 2 ,A 5	3
A 1 ,A 2 ,A 3	2

(e) C 3

Pattern mining can be of many forms and various other fields can be easily merged in this. One of such new fields is the temporal association rule mining. It consists of the temporal i.e. concept of time in it. Detailed explanation of this topic has been done further.

• C. Temporal Association Rule Mining

Temporal Data Mining is a rapidly evolving expanse of investigation that is at the connection of numerous disciplines, containing statistics (e.g., time series analysis), temporal pattern acknowledgement, temporal files, optimization, conception, high-performance computing, and parallel computing. This paper is used to serve as an outline of the temporal information mining in exploration and applications. In addition to giving a typical summary, we move the criticalness of temporal information mining issues inside (KDTD) Knowledge Discovery in Temporal Databases which incorporate definitions of the essential classifications of temporal information mining methodologies, models, techniques and couple of other related areas [5].

The task include for temporal data mining are:

• •    Data characterization and comparison

• •    Temporal clustering analysis.

The temporal information mining piece of the KDTD (Knowledge Discovery in Temporal Databases) system is concerned with the algorithmic means through which temporal patterns are expelled and numbers from worldly information. Temporal Data Mining is a solitary stage in the methodology of (KDTD) Knowledge Discovery in Temporal Databases that models and temporal patterns(enumerates structures) completed the temporal data and any calculation that identifies temporal patterns

from, on the other hand, fits models to, worldly information is a Temporal Data Mining Algorithm [16]. Basically, temporal information mining is concerned with the investigation of temporal information and for temporal worldly patterns and regularities in sets of fleeting data. Additionally temporal information mining frameworks grant for the likelihood of PC driven, programmed investigation of the data. Temporal information mining has prompted a novel method for associating with a worldly database [6]. Steps in temporal data mining are:-

• •    Data  pre-processing. In data pre-processing

includes data cleaning, integration, exchange and reduction. By this we get good quality of data mining object. It is one of the most necessary step in data mining.

• •    To find the frequent itemsets which have the support no less that min_s;

• •    Generate association rules with frequent itemsets. Without time generate association rule is different, but it adds time information on frequent itemsets. So here the association rules are temporal ones;

• •    To generate rule sets and output.

Temporal data mining tends to work from the data up and the best known procedures are those created with an introduction towards substantial volumes of time related data, making use of gathered temporal data as much as possible to arrive at reliable conclusions.

• D. Rough Sets

In the rough set theory, membership is not the primary concept. Rough sets represent a different mathematical approach to vagueness and uncertainty. Description of a set in the harsh set hypothesis is identified with our data, learning and discernment about components of the universe. At the end of the day, we "see" components of the universe in the setting of accessible data about them. As a result, two unique components can be incongruous in the connection of the data about them and "seen" as the same. The rough set methodology is based on the premise that lowering the degree of precision in the data makes the data pattern more visible, whereas the central premise of the rough set philosophy is that the knowledge consists in the ability of classification. In other words, the rough set approach can be considered as a formal framework for discovering facts from imperfect data. The results of the rough set approach are presented in the form of classification or rules derived from a set of examples [7].

Rough set theory has discovered numerous interesting applications [8]. The rough set methodology seems to be of fundamental significance to AI and cognitive sciences, particularly in the areas of pattern recognition, expert systems, machine learning, decision analysis, knowledge acquisition, knowledge discovery from databases and inductive reasoning.

The main advantage of rough set theory in data analysis is that it does not need any extra knowledge or any preliminary about the data.

Rough set theory [17] is still another approach to vagueness. Similarly to the fuzzy set theory it is not an alternative approach to a theory of the classical set but it is embedded in it. Theory of rough set can be seen as a particular operation of the vagueness i.e., roughness in this method is defined through a boundary region of a set, and not through a partial membership, like in the theory of fuzzy set.

• •    Lower approximation of the set X with respect to R is the set of each object, which can be for the certain categorized as X with respect to the R (are certainly X with respect to R).

R* ( X ) = { x e U : R ( x ) c X .         (3)

• •    The upper approximation of a set X with respect to R is the set of the each object which can be probably categorized as X, with respect to R (are possibly X in the vision of R).

R * ( X ) = { x e U : R ( x ) n X * ф .        (4)

• •    The boundary region of a set X with respect to R is the set of the each object, which can be categorized neither as X nor as not-X with respect to R.

R ( X ) = R * ( X ) - R * ( X ) .           (5)

Accuracy of approximation can also be characterized numerically by the following coefficient.

^a R ⁽ X ) =

| R * ( x ) |

| R *( x ) |.

where |X| denotes the cardinality of X.

• •    0 <  a ( X ) < 1 . If a ( X ) = 1 . Set X is crisp

(exact with respect to the R), if the boundary region of X is empty.

• •    ^a R ^{( X} ) <  1. Set X is rough (inexact with respect

to the R), if the boundary region of X is nonempty.

Thus, a set is rough if it has a nonempty boundary region; otherwise the set is the crisp [18]. The application of rough set is mentioned in the example in the proposed work. The example shows the correct us of rough set. The rough set thus explains a better way to work so as to optimize the results.

• II.    Related Work

Omari et al., [11] developed a new temporal measure for interesting frequent itemset mining. Frequent item set mining helps in searching for powerfully associated items and transactions in large transaction databases. This measure is based on the fact that interesting frequent item sets are typically covered by several recent transactions. This minimizes the cost of searching for frequent item sets by minimizing the search interval. Additionally, this measure can be used to enhance the search approach implemented with the Apriori Algorithm.

Association Rules Algorithm and Rough Set Theory are mining approaches in which it is used to recognize implicit rules from great quantities of data. As the Algorithm of Association Rules Mining, Apriori Algorithm has achieved a lot of application owing to its easy use. On the other hand, in practice, it often comes across problems such as low mining efficiency. Hence, many invalid rules are attained and the rules of pattern mining disorder. An algorithm called R_Apriori is created by Chen Chu-xiang et al., [12] for the problems with the decision-making domain. Initially, the cores situations are mined with Algorithm of the Rough Attribute Reduction, 1-frequent item sets, and the corresponding sample set is then created with use mining cores set through the Apriori Algorithm. After the abovementioned stage, the multi- stage frequent item sets and the corresponding confidence and support can be gained through the sample set intersection operator. Consistent with the confidence degree and support, the corresponding strength of the rule is determined. R_Apriori Algorithm resolves the problems of Apriori Algorithm to recover the effectiveness of the algorithm and is in the campaign on certain significance.

Market Basket Analysis is the most important function of information discovery in databases. All things considered, market creates databases, for the most part, contain temporal coherence, which couldn't catch by means of standard association rule mining. Therefore, there is a requirement for creating calculations that show such transient cognizance's inside the information. Schluter et al., accumulates various thoughts of temporal affiliation principles and presents a system for mining a large portion of these sort (calendar-based, cyclic - and lifespan)in a business basket database, improved by two new tree structures. These two tree structures are called as EP-and ET-Tree, which are obtained from available systems enhancing standard affiliation guideline mining. They are utilized as a representation of the database and henceforth make the revelation of temporal association rules which are extremely proficient. There have been at various modern ponders in the field of periodic pattern mining.

Ozden et al.[13] issue characterized the which is based on finding cyclic affiliation controls as discovering cyclic associations between things vicinity inside of exchange. In their examination, the data was an exchange situated, in which all comprised of an arrangement of things. Moreover, every exchange was labeled with a season of execution. Through studying the connection between time and association rules, they connected three heuristics: cycle elimination, cycle pruning and cycle skipping to discover cyclic association rules in the value-based databases.

Han et al.[14] shown a couple of calculations to adequately mine partial periodic patterns, by exploring few features partial periodicity related, such as an Apriori feature and also max-sub pattern hit sets a feature, and through shared mining of multiple times. In order to phase the restriction cyclic association rule, Han, et al. Utilized certainty as a part of the measure how is a periodic pattern vital. The assurance of a describe pattern as the event tally of the pattern over the most extreme measure of example length periods in the worldly database.

Owing to a big amount of applications periodic pattern mining has been widely studied for over a decade. The Periodic pattern is a pattern that recurrences itself with a particular period in a provide sequence. Periodic patterns can be mined from datasets like social networks, biological sequences and continuous, discrete time series data and spatial-temporal data. Periodic patterns are categorized based on several conditions. Periodic patterns are classified as frequent periodic patterns and statistically important patterns which are based on the frequency of occurrence. Frequent periodic patterns are in turn categorized as imperfect and perfect periodic patterns, partial and full periodic pattern, asynchronous and synchronous periodic patterns, approximate periodic patterns, dense periodic patterns. A pattern which happens periodically without any misalignment is known as a pattern of synchronous periodic. In this paper has used the synchronous periodic data mining in our proposed because most of the festivals are coming in the same months.

R. Raghavan and B.K.Tripathy[19] have proposed two inclusion rules for pessimistic cases. For different six cases they shown by examples that correct inclusions hold true. On the basis of classification approximation a theorem given by Tripathy et.al that establish sufficient type properties. They established that result is sufficient and necessary one. For this consider types of elements in classification with respect to both types of multigranulations and establish a general theorem on them.

Xuan Thao Nguyen, Van Dinh Nguyen and Doan Dong Nguyen [20] have proposed the rough fuzzy relation on Cartesian product of two universe sets is defined, and then the algebraic properties of them, such as the max, min, and composition of two rough fuzzy relations are examined. Finally, reflexive, α- reflexive, symmetric and transitive rough fuzzy relations on two universe sets are also defined.

K. Lavanya, N.Ch.S.N. Iyengar, M.A. Saleem Durai and T. Raguchander [21] have proposed an approach based on rough set that improved the quality of agricultural data through elimination of redundant and missing attributes. The data formed after pretreatment were target information, and used attribute reduction algorithm that derive rules. The generated rules were used that structure the nutrition management decision making.

The experiments with precision above 80% shows the results feasibility of the developed decision support system for nutrient management. The optimized fertilizer usage for better yield of rice cultivation is influenced by key factors like soil fertility, crop variety, duration, season, nutrient content of the fertilizer, time of application etc.

Essam Al Daoud [22] have proposed various techniques and combined with harmony search such as use of balanced fitness function, fussing the classical ranking methods with fuzzy rough scheme and applying binary operations to accelerate implementation. The experiments on 18 datasets explained the efficiency of suggested algorithm and shows the effieciency of new algorithm. Remove the misleading, redundant and unrelated features that increase the learning accuracy. Fuzzy rough set offers formal mathematical tools to reduce the number of attributes and determine the minimal subset.

• III.    Proposed Work

In this paper has proposed a new Apriori based approach for mining periodic frequent patterns from the temporal database. The concept of the rough set theory is used so as to reduce the number of unnecessary itemsets or records. And the periodic mining tells about the occurrences of periodical frequent patterns in the synchronous or asynchronous mode in events.

The whole proposed process is explained here with the help of flowchart, algorithm and an example with a seasonal temporal database of festivals that occur in the months of a year.

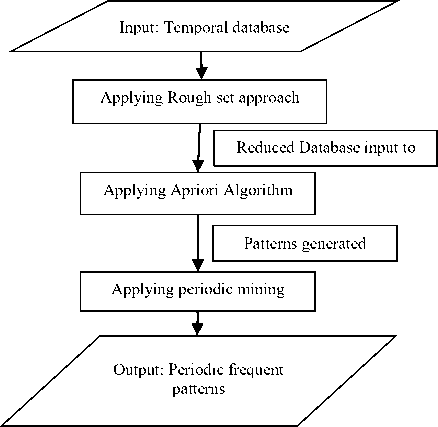
Fig.1. Flowchart of Proposed Algorithm

This flowchart explains the whole process of the proposed algorithm. The above figure gives a clear idea about proposed algorithm. The algorithm has been explained below:-

H => High

A => Average

L => Low

Y => Yes

N => No

• A.    Proposed Algorithm

Input: Temporal database, min. support, min. confidence. Output: Profitable frequent patterns.

• 1.    First initiate the temporal dataset that contains the values such as high, average and low of selling of products in different festivals showed as YES and NO.

• 2.    Applying Rough Set Theory, to create the reduced table with the help of Boundary values. Reduced table contains only that records which contain upper boundary value.

• 3.    Then applying Apriori algorithm to generate frequent patterns, before it taking the value of high, average and low in the form of 0 and 1 i.e. called binary conversion. H = 1, A≅ 0, L = 0

• 4.    Now generated best frequent patterns for a year.

• 5.    Similarly, Apply steps 1 to 4 again, for the previous 4 years to generated best frequent patterns.

• 6.    Then Apply Periodic Mining to extract profitable periodic frequent patterns from previous 5 years.

• B.    Example

There is the Seasonal Temporal database that contains conditional and decisional attributes where Sweets, Cloths, Accessories, Flowers, and P.Frames (S, C, A, F, P.F) are condition attributes, Festivals is decisional attribute and there is one more attribute Month/Year which shows the time sequenced in the form of month and year. It is the data representation of 1 year showing 12 months of the year. Various attributes have also been shown so as to make the diversified database. The data is shown in the form of a table 2 in the example below.

Table 2. Temporal Dataset

ID	Month/Year	S	C	A	F	P.F	Festivals
1	1/14	H	H	L	H	L	Y
2	2/14	L	L	L	H	H	N
3	3/14	H	H	H	H	L	Y
4	4/14	H	H	H	L	H	Y
5	5/14	L	L	L	H	L	N
6	6/14	H	L	H	L	L	N
7	7/14	H	H	L	H	L	Y
8	8/14	H	H	H	H	H	Y
9	9/14	A	L	L	H	L	N
10	10/14	A	H	H	H	H	Y
11	11/14	H	H	H	H	L	Y
12	12/14	A	H	H	H	H	Y
	……	…..	…..	……	…..	……	……

For Sweets:-

H > 1000

500 < A < 1000

L < 500

For Clothes:-

H > 500

L < 500

For others (Accessories, Flowers, P.Frames):-

H > 1000

L < 1000

Now applying Rough Set Theory (RST)

Boundary values:-

Lower Approximation = {3, 4, 8, 10, 11, 12}

Upper Approximation = {1, 3, 4, 7, 8, 10, 11, 12}

Accuracy of Approximation = 6/8 = .75

Table 3. Reduced Table

ID	Month/Year	S	C	A	F	P.F	Festivals
1	1/14	H	H	L	H	L	Y
2	3/14	H	H	H	H	L	Y
3	4/14	H	H	H	L	H	Y
4	7/14	H	H	L	H	L	Y
5	8/14	H	H	H	H	H	Y
6	10/14	A	H	H	H	H	Y
7	11/14	H	H	H	H	L	Y
8	12/14	A	H	H	H	H	Y

Now applying Apriori algorithm to generate frequent patterns.

Here taking,

H = 1

A≅0

L = 0

Table 4. Binary representation of Reduced Table

ID	Month/Year	S	C	A	F	P.F	Festivals
1	1/14	1	1	0	1	0	Y
2	3/14	1	1	1	1	0	Y
3	4/14	1	1	1	0	1	Y
4	7/14	1	1	0	1	0	Y
5	8/14	1	1	1	1	1	Y
6	10/14	0	1	1	1	1	Y
7	11/14	1	1	1	1	0	Y
8	12/14	0	1	1	1	1	Y

Step-I

{Sweets} = {6}

{Clothes} = {8}

{Accessories} = {6}

{Flowers} = {7}

{P. Frames} = {4}

Taking minimum support factor as = > 4.

So, the frequent items are = {Sweets, Clothes, Accessories, Flowers, P. Frames}

Step-II

{Sweets, Clothes} = {6}

{Sweets, Accessories} = {4}

{Sweets, Flowers} = {5}

{Sweets, P.Frames} = {2}

{Clothes, Accessories} = {6}

{Clothes, Flowers} = {7}

{Clothes, P.Frames}= {4}

{Accessories, Flowers} = {5} {Accessories, P.Frames} = {4} {Flowers, P.Frames} = {3}

So, the frequent items set are = {{Sweets, Clothes}, {Sweets, Accessories}, {Sweets, Flowers}, {Clothes, Accessories}, {Clothes, Flowers}, {Clothes, P.Frames}, {Accessories, Flowers}, {Accessories, P.Frames}}

Step-III

{Sweets, Clothes, Accessories} = {4}

{Sweets, Clothes, Flowers} = {5}

{Sweets, Accessories, Flowers} = {3}

{Clothes, Accessories, Flowers} = {5}

{Clothes, Accessories, P.Frames} = {4} {Clothes, Flowers, P.Frames} = {3} {Accessories, Flowers, P.Frames} = {3}

So, the frequent items set are = {{Sweets, Clothes, Accessories}, {Sweets, Clothes, Flowers}, {Clothes, Accessories, Flowers}, {Cloths, Accessories, P.Frames}}

Step-IV

{Sweets, Clothes, Accessories, Flowers} = {3}

{Sweets, Clothes, Accessories, P.Frames} = {3}

So, the generated frequent patterns are = {О}

So based on Apriori algorithm frequent items generated, to sort the values and the generated frequent items, we will remove the single and 2-paired items generated so as to find out the best patterns. So, the best patterns generated for this year 2014 are:-

{{Sweets, Clothes, Accessories}, {Sweets, Clothes, Flowers}, {Clothes, Accessories, Flowers}, {Sweets, Accessories, P.Frames}}

Similarly, the data for the previous 4 years is calculated based on the tables generated for the previous years. So, the frequent patterns generated for the previous four years are shown in table 5 below:-

Table 5. Generated frequent patterns of five years

Years	Frequent Patterns
2014	{Sweets, Clothes, Accessories}, {Sweets, Clothes, Flowers}, {Clothes, Accessories, Flowers}, {Sweets, Accessories, P.Frames}
2013	{Sweets, Clothes, Accessories}, {Sweets, Clothes, Flowers}, {Clothes, Accessories, Flowers}, {Sweets, Accessories, P.Frames}
2012	{Sweets, Clothes, Accessories}, {Sweets, Clothes, Flowers}, {Clothes, Accessories, Flowers}, {Sweets, Accessories, P.Frames}
2011	{Sweets, Clothes, Accessories}, {Sweets, Clothes, Flowers}, {Clothes, Accessories, Flowers}, {Sweets, Accessories, P.Frames}
2010	{Sweets, Clothes, Accessories}, {Sweets, Clothes, Flowers}, {Clothes, Accessories, Flowers}, {Sweets, Accessories, P.Frames}

So, based on the periodic mining algorithm, the common patterns are generated for the 5 years shows the frequent patterns and thus give the ideas about the seasonal buying behavior of items in festivals that have been occurring periodically in the past 5 years. A configuration which ensures intermittently deprived of some misalignment is known as the synchronous periodic pattern. Here occurs synchronous periodic pattern during 5 years and as more buying concern profitable periodic frequent patterns are:-

{Sweets, Clothes, Accessories}, {Sweets, Clothes, Flowers}, {Clothes, Accessories, Flowers}, {Sweets, Accessories, P.Frames}

• IV.    Result Analysis

The results obtained after applying the whole algorithm have been found out. The results generated are shown in the following manner. The patterns are generated that are periodically frequent on the basis of the data for past 5 years. The generated patterns in table 6 are:-

Table 6. Periodic Frequent Patterns

Periodic Frequent Patterns

{Sweets, Clothes, Accessories}, {Sweets, Clothes, Flowers}, {Clothes, Accessories, Flowers}, {Sweets, Accessories, P.Frames}

These results are shown with the various patterns generated for the algorithm applied. They are better in the sense that they are temporal and not redundant. The rough set reduces the unnecessary patterns generated.

• V.    Conclusion

This paper has proposed a new rough set based approach for extracting periodic frequent patterns. Due to the use of rough set based concept, proposed approach considers only the reducts of the initial database. Hence, it is clear that the proposed approach works on the reduced database which leads to the enhancement in the performance. Furthermore, proposed approach makes use of the Apriori approach, which helps in exposing periodic frequent patterns that may also be considered for the profitable decision-making process.

• [1]    J. Han and M. Kamber , “Data Mining: Concepts and Techniques”, 2nd ed.,The Morgan Kaufmann Series in Data Management Systems, Jim Gray, Series Editor 2006.

• [2]    U. M. Fayyad, G. P. Shapiro and P. Smyth, From Data Mining to Knowledge Discovery in Databases. 07384602-1996, AI Magazine (Fall 1996).pp: 37–53.

• [3]    J. Han and M. Kamber, Data Mining: Concepts and Techniques. Second edition Morgan Kaufmann Publishers.

• [4]    RakeshAgrawal, SaktiGhosh, Tomasz Imielinski, BalaIyer, and Arun Swami, An Interval Classier for Database Mining Applications", VLDB-92 , Vancouver, British Columbia, 1992, 560-573.

• [5]    D. Heckerman, H. Mannila, D. Pregibon, and R. Uthurusamy, editors. Proceedings of the Third International Conference on Knowledge Discovery and Data Mining (KDD-97).AAAI Press, 1997.

• [6]    R. Slowinski, J. Stefanowski, Rough Classification with Valued Closeness Relation, in: E. Diday, Y. Lechevallier, M. Schader, P. Bertrand, B. Burtschy_Eds.., New Approaches in Classification and Data Analysis, Springer, Berlin, 1994.

• [7]    E. Simoudis, J. W. Han, and U. Fayyad, editors.Proceedings of the Second International Conference on Knowledge Discovery and Data Mining (KDD-96).AAAI Press, 1996.

• [8]    Y. Maeda, K. Senoo, H. Tanaka: Interval density function in conflict analysis, in: N. Zhong, A. Skowron, S. Ohsuga, (eds.), New Directions in Rough Sets, Data Mining and Granular-Soft Computing, Springer, 1999, 382-389.

• [9]    J. Yang, W. Wang, and P.S. Yu.Mining asynchronous periodic patterns in time series data. IEEE Transaction on Knowledge and Data Engineering, 15(3):613-628, 2003.

• [10]    Omari et.al. new temporal measure for association rule mining. Second International Conference on Knowledge Discovery and Data Mining,1997.

• [11]    Chen Chu-xiang, Shen Jiang-jing, Chen Bing, et al., “An Improvement Apriori Arithmetic Based on Rough Set Theory”, In proceeding of the 2011 Third Pacific-Asia Conference on Circuits, Communications and System (PACCS). pp.1-3, 2011.

• [12]    B. Ozden, S. Ramaswamy, and A. Silberschatz.Cyclic association rules.     In Proc.     of the    14th

  InternationalConference on Data Engineering, , pages 412–421, 1998.

• [13]    J. Han, G. Dong, and Y. Yin.Efficient mining paritial periodic patterns in time series database. In Proc. of the15th International Conference on Data Engineering, ,pages 106–115, 1999.

• [14]    Agrawal, R., Imielinski, T., and Swami, A. N. 1993. Mining association rules between sets of items in large databases. In Proceedings of the 1993 ACM SIGMOD International Conference on Management of Data, 207216.

• [15]    Dixit et al.,”A Survey of Various Association Rule Mining Approaches” International Journal of Advanced Research in Computer Science and Software Engineering 4(3), March - 2014, pp. 651-655.

• [16]    Pradnya A. Shirsath, Vijay Kumar Verma, “A Recent Survey on Incremental Temporal Association Rule Mining”, International Journal of Innovative Technology and Exploring Engineering (IJITEE) ISSN: 2278-3075, Volume-3, Issue-1, June 2013.

• [17]    Yiyu Yao, “Rough Set Approximations: A Concept Analysis Point Of View”, University of Regina, Regina, Saskatchewan, Canada, 2015.

• [18]    En-Bing Lin and Yu-RuSyau, “Comparisons between Rough Set Based and Computational Applications in Data Mining”, International Journal of Machine Learning and Computing, Vol. 4, No. 4, August 2014.

• [19]    R. Raghavan and B.K.Tripathy,” On Some Comparison Properties of Rough Sets Based on Multigranulations and Types of Multigranular Approximations of Classifications”, I.J. Intelligent Systems and Applications, 2013, 06, 70-77.

• [20]    Xuan Thao Nguyen, Van Dinh Nguyen and Doan Dong Nguyen,” Rough Fuzzy Relation on Two Universal Sets”, I.J. Intelligent Systems and Applications, 2014, 04, 49-55.

• [21]    K. Lavanya, N.Ch.S.N. Iyengar, M.A. Saleem Durai and T. Raguchander, “Rough Set Model for Nutrition Management in Site Specific Rice Growing Areas”, I.J. Intelligent Systems and Applications, 2014, 10, 77-86.

• [22]    Essam Al Daoud, “An Efficient Algorithm for Finding a Fuzzy Rough Set Reduct Using an Improved Harmony Search”, I.J. Modern Education and Computer Science, 2015, 2, 16-23.