On the weak convergence of operators iterations in von Neumann algebras

This paper is devoted to ergodic type properties of the weak convergence of operators iterations in von Neumann algebras.

The first results in the field of non-commutative ergodic theory were obtained by Sinai and Anshelevich [18] and Lance [14]. Developments of the subject are reflected in the monographs of Jajte [9] and Krengel [13] (see also [4]—[7], [10], [11], [16]).

We will use facts and the terminology from the general theory of von Neumann algebras ([1], [2], [15], [17], [19]).

Let M be a. von Neumann algebra, acting on a. separable Hilbert space H, M* is a. preconjugate space of M, which always exists according to the Sakai theorem [17].

Recall some standard terminology ([4], [5], [6], [10], [11], [13]).

DEFINITION 1. A linear mapping T from M, in itself is called a. contraction if its norm is not greater then one.

Definition 2. A contraction T is said to be positive if ТД. c M>..

We will consider two topologies on the space My the weak topology, or the o^M*,M^ topology, and the strong topology of the M^-space norm convergence.

DEFINITION 3. A matrix (а„Д i,n = 1, 2,... of real numbers is called uniformly regular, if:

DC sup 5 a„ г < C < oo, lim sup a„ f = 0, lim / a„ г = 1.

n —'     ’                     Tl—^OO ;      1            n^-oo         ’ г=1                                                             г

• 2.    Main Result

The following theorem is valid:

Theorem 1. The following conditions for a. positive contraction T in the pre-conjugate space of a. von Neumann algebras M are equivalent:

• (i)    The sequence {T²}^!^,... converges weakly;

Author is thankful to Professor Michael S. Goldstein (University of Toronto, Canada) for helpful discussions.

• (ii)    For each strictly increasing sequence of natural numbers {fci)i=i,2,..., _n-i^2_T^k\ i

converges strongly;

(hi) For any uniformly regular matrix (a„jZ), the sequence {A„(T)}„=1j2,..., АДТ) = ^апДП, г converges strongly.

< We first prove the following lemma:

Lemma 1. Let there exists a uniformly regular matrix (a„_jZ) such that for each strictly increasing sequence {ki}i=i,2,... of natural numbers,

Bn = Van tTki, г

converges strongly. Then the sequence {T¹}^!^,... converges weakly.

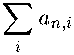
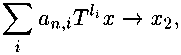
as n —> oo. For a matrix (a„jZ) let us build increasing sequences {ij}j=i,2i... and {n?}j=i,2,...> such that lim j^oo

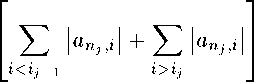
= 0.

Let

m; = k; for г E [?2j-i, ^2j) and m; = I; for г E [?2j, ^2j+i), 7 = 1,2,...

Then lim j

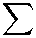
/pm, _

= 0,

lim j

^а_П2]/Г^т1х - ж₂ i

= о,

which contradicts (1), and therefore жх = Ж2- Let now у E M is such that

(Тпж - жьу) н- 0, when п —> oo. Let us choose a subsequence {k^ such that (Т^ж-Ж1,у) -^7^0, where 7 is a real number. Then, from the uniform regularity of the matrix (a„jZ) it follows that lim ^«„^Т^'ж-ж^у =7, which contradicts the choice of the matrix (an,i). >

[Proof of the Theorem 1 (cont.).] Because the implication (ii) =^ (iii) is obvious, the implications (ii) =^ (iii) =^ (i) immediately follow from the lemma 1.

The implication (iii) =^ (ii) is trivial, because the matrix (а„Д a„_jZ = у 52 ^j,k, ^1S г<п uniformly regular.

Applying the above with lemma 1, а_П1, = ±, i ^ n and a^ = 0 for г > n, we get the implication (ii) =^ (i).

To prove the implication (i) =^ (ii), we would need the following lemma:

Lemma 2. Let Q be a contraction in the Hilbert space H. Then the weak convergence of Q"x in H, where x G H, implies the strong convergence of

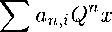
г

for any uniformly regular matrix ^a^.

< If the weak limit Qⁿx exists and is equal to xi, then

Qxi = Q( lim Q^x^ = xi, Tl^OO where the limit is considered in the weak topology, i. e. x\ is Q-invariant. Therefore

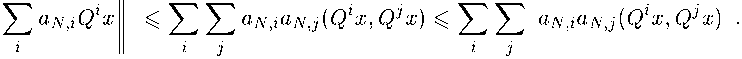
Let us fix e > 0. Because Q is a contraction, the limit ||<9^пж|| does exist. Now, we can find К > 0, such that for к > К and 7 > 0,

||q^|| - ||у^ж|| <  e²

and

(Q^kx, ж) < E.

Then,

(У^ж) - (Q^k+ix,Qix^ = (У^ж) - (Q*^jQ^k+jx,x^

• <    ||q^ - у*^^ж|| • Цж|| = (|^ж- q^q^|Q ² ■ и

• = (||q^||2 - 2 Цу^Ц2 + Цсгу^Ц2) 2

• <    (J|Q^||2-||Q*4r||2y M

and therefore

^Q^k^x,Q3x^ < _£ • (1 + ||ж||)

for all к > К and j ^ 0, or for г — j\ ^ к the inequality

\№^\ < E . (1 + ||Ж||);

is valid. We will fix r/ > 0, and let N be such a natural number with max, a_nj, < r/, for n >  N. Then the expression (1) for n ^ N could be estimated the following way:

££|_WMW^QXQ^U £ W^x^ x^\

• * j                               \i-j\^k                            \i—j\>k

^£M-HHP2A;-i) + ££|a^^

^ C ■ у ■ ||ж||2 ■ (2A: — 1) + C2 ■ £ ■ (1 + ||ж||).

From the arbitrarity of the values of £ and у it follows that the strong convergence is present and the lemma is proven. >

[Proof of the Theorem 1 (cont.).] Let us prove the implication (i) =^ (iii). Let x E M„ ■ and the sequence {T1x}i=ii2,... converges weakly. Without loss of generality we can consider ||ж|| < 1, and let x = lim T^x, n—^oo where the limit is understood in the weak sense. Let us consider oo

У = £2~^пТ^пж.

n=0

The series that defines у is convergent in the norm of the space M*. From the positivity of x and the properties of the operator T it follows that Ту ^ 2y, and, therefore, for all к = 1,2,... , s^T^ky^ < s(y), where by s(^) we denote the support of the normal functional z.

Lemma 3. Let и E M*^ and s(u) < s(y). Then s^ < з(ж), where й = lim T4.

n^-CXD

• < Indeed, let us fix _£ > 0. From the density of the set

£ = {w E M_. w < Ay, for someA > 0}, in the set

6 = {w E Mt+, s^to) < s(y)}, in the norm of the space M* it follows that there are A > 0 and го E £ such that

||w — w|| < _£ and го < Ay.

Let го = Ишп-юо Tⁿw. Then

w(l —з(ж)) = lim (Tⁿ(w))(l-s(^)) ^ A- lim (Т^пу)(1-з(ж)) п—УОО                                TL—>-(X)

гжК1-Ау! n—>oo \ —'

\Zc=O

= a£2 6 lim (Тп+^ж) (1—s (ж)) = 0. ^—'    n^-oo k=Q

Because the operator T does not increase the norm of the functionals from M„ we get that

й(1-з(ж)) = lim (Т^пи)(1-з(ж)) < lim (Tⁿw)(l-sp)) + lim ||Tⁿ(w-u)|| <  e. n—^oo                       ti^-oq                      ti^-oq

The needed inequality follows, since e is arbitrary. >

[Proof of the Theorem 1 (cont.).] Let now p E M*. We will denote by p.E, where E is a projection from the algebra M, the functional

Vp.E^ = p^EAEY where A E M. Let us fix e > 0. We will find a number N, such that

(Т^пж)(1-з(ж)) <  e²

for n >  N. Thus,

ЦЛ.^ж) -ЛЦ = sup (T^Mjl-spjjAjl-sp))) aem

Mlloc^l

+ (А)(№))А(1-₈(й))) + (Т"ж)((1-8(ж))Л(8(ж))) < £ ■ (e + 2 hp): because

\р^\Чр(А*АУр(В^

where p E M_t; and А, В E M.

Let w E Sis such that го < Аж for some A > 0 and ЦТ^ж.зр) — w|| <  e. Then, for n > N, the following is valid:

||Т"ж-T"~ww|| < ||T" рТ^ж-Т^ж.^ж))]]

+ ЦТ^рТ^ж.бр)-w)|| <  4-е.               ^1,2,1

By taking the weak limit in the inequality (2) and because the unit ball of M, is weakly closed, we will get ||ж — w|| < 4 • e, where w = linin-юо Т^пго.

Let us now consider the algebra M_s^. The functional ж is faithful on the algebra M_s^y We will consider the representation тгу of the algebra M,^) constructed using the functional ж [2]. Because the functional ж is faithful, we can conclude that the representation тг^ is faithful on the algebra M_s^, and therefore тг- is an isomorphism of the algebra M_s^ and some algebra 21. The algebra 21 is a von Neumann algebra, and its pre-conjugate space 21* is isomorphic to the space М*.з(ж) ([17]). Let us note now that

ТМ*.б(ж) C M^.s^xY

In fact, T£ C £, and therefore, by taking the norm closure we get TS C S; by taking now the linear span we will get

ТМ*.б(ж) C M^.s^xY

Denote by T the isomorphic image of the operator T, acting on the space 21*. Let и E 2l*₊ and u ^ Аж for some A > 0. Then there exists the operator В E 21', where 21' is a commutant of 21, such that (ABQ, Q) = u(A) for all A E 21. Note, that from the lemma 2

(Tu)(A) = ЩТУА^ = (((T)*A)BQ,Q) = (A((T*)'B)Q, Q).

Also, from

T2l*+ C 2l*+, Ц^Ц < ||u|| and Tx = x it follows that

(ТГ21+;(Т*)Ю and IKTjML^HL for all A E 21. Based on the lemma we now conclude that

II^L^IIBL; ТХС 2l'+; T*X1

for all В G 21'.

The space 2l'_so is a pre-Hilbert space of the self adjoint operators from 21' with the scalar product ^3,0^- = (CBQ,Q), and, using the Kadison inequality [1] we have

((T*'b)(T*'b)Q,Q) < (T*'(B2)Q,Q) < (BQ,BQ), i. e. the operator T*' is a contraction in the pre-Hilbert space (2l'sa, (•, D-

We will identify M*.s^ and 21*. Because го G £, i. e. го < Xx for some A > 0, then w < Xx as well. Let

w(A) = (BAQ, Q) and w(A) = (BAQ,Q)

for all A G 21, where В, В G 21'.

Let now (a„_jZ) be a uniformly regular matrix. Using lemma 2 we will find к E N so that

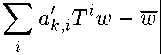
sup леа Hlloc=l

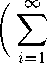
ОО                            OO                        \ 2

£ а'_кДТ^ЧВ - B)Q £ a'_kXY^ - В) i=l                      г=1                   /

sup леа PIU^i

(AQ, AQ) 2

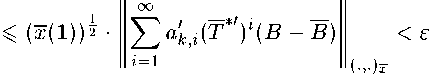
for к > К, where by («W) we will denote a matrix with the elements

а

I тцг

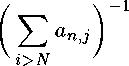
It is easy to see that the matrix («W) will be uniformly regular as well. Then, for a big enough к > К we will have

< £ ИД\\T^lx - t|| + £ l^aud 11^Гж - T^l-^Nto\\

i>N

i^N

+ 52 \^акД ■ i>N

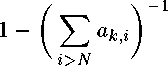
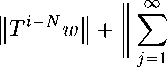
^ ' O-k,! i>N

-1

Т]го — го

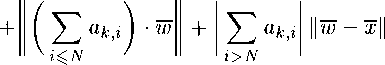
52 2 ■ tv+ 52 \ак^ ■4e + 52 \ак^ u - u +£) x) ■2 + 52 2 ■ др+ ^ + e) ■4e i^N       i>N          i>N                      i^N

< 2e + (1 + e) • 4e + E • 2 • (1 + e) + E + 2e + (1 + e) • 4e < 25s.

The arbitrarily of e proves the needed statement. The proof of the theorem is now completed. >

REMARK. Extention of the discussed properties of iterations to non-commutative L_p- spaces will be separately presented in the forthcoming paper [12].