On time selection for track possession assignment at the railway station

One of the aims of both European railways and JSC “Russian Railways” is to increase the number of transported cargoes and passengers. This leads to the problem on increase in the capacity of railway stations and hauls.

Most papers devoted to the improvement of the railway traffic are related to the optimization of the traffic at hauls. Among other publications, we note [1–5]. The paper [1] gives a detailed review of studies on scheduling and cargo traffic. The paper [2] considers the problem to construct a cyclical schedule such that a train of a certain destination leaves a certain station at the same time every cycle, for example, every half hour or every hour. In [3, 4], the problem of locomotive delivery and transportation plans is solved. In [5], the same problem is solved taking into account the random delay in the readiness of a train for departure.

At the same time, a station with increase in traffic volumes plays no less important role than hauls. Indeed, the low capacity of the station can level down the entire positive effect of increase in the capacity of hauls. However, note that optimization of traffic at the station receives less attention than incidents and traffic on hauls. Among other works, we note [6–8]. The paper [6] investigates the problem to determine the arrival/departure time of a freight train to the station and the arrival platform. A simulation model of railway station functioning is presented in [7]. The paper [8] sets and solves the problem to optimize traffic of shunting trains around the station. Note that the necessary repairs at the station can also lead to decrease in capacity. Therefore, there exists the problem on track possession. The problem is to determine the time during which the train traffic on the haul, individual railway tracks of the haul or the railway station is interrupted for the repair and construction works [9].

Researches on track possession assignment are carried out for railway hauls and can be divided into several groups. One part of researches is devoted to the problem of track possession assignment based on the forecast of the state (degradation) of the railway infrastructure, the repairs cost, and the rail traffic volume [10–12]. The other part is devoted to the issue of track possession assignment based on the current schedule [13–15]. The paper [13] considers the problem of assigning technical brigades to maintain tracks. To this end, the paper [13] takes into account possible delays both in the train schedule and in the execution of technical works during the vacant time, when the tracks are free from passenger/freight trains. The optimization criterion is to minimize both the nonfulfillment of the basic schedule and the time execution of all planned technical works. The paper [13] assumes that the time is discrete (the discretization interval is equal to 1 second). This assumption is necessary, since extremely heavy traffic leads to a huge number of optimized variables in the proposed model. At the same time, the obtained problem of mathematical programming is nonlinear. The paper [14] considers a single-track railway with sidings, for which the entire original schedule of freight trains is restructured taking into account the need to hold track possessions on some sections of the track. In this case, the possession time is interpreted as a pseudo-train and can be transferred in time. The paper [15] considers a general view on a railway network, in which track possession can be transferred in time and trains can be canceled, delayed, or departed along different routes. The optimization criterion is to minimize adjustments to the original schedule of passenger/freight trains. However, the approach of simultaneous scheduling of passenger/freight trains and track possession used by [14, 15] cannot be transferred to the station. Indeed, passenger/freight trains carry out shunting operations, and it is necessary to change the execution schedule of these operations, as well as the routes of shunting locomotives, the searching for which is the subject of an individual study [8].

At present paper, we investigate the problem on track possession assignment at the railway station. To this end, we use various criterions that correlate with criterions from [13–15]. Namely, we use the following items as criterions for assignment:

• •    time interval with maximum length during which all track sections to be repaired are vacant simultaneously,

• •    time interval with duration that is not less than the duration of the specified time interval in which the number of occupied track sections to be repaired is minimal,

• •    time interval with duration that is not less than the duration of the specified time interval in which the number of delayed (postponed) passenger/freight trains going through the track to be repaired is minimal.

All problems are solved using mixed integer linear programming methods. A meaningful example is considered.

1.    Notation and Basic Assumptions

Consider an undirected graph of the railway station G =< V,E >, where V is a set of vertices (switches, joints between rails and entry (exit) points of the station (station boundaries)) and E is a set of edges (railway tracks) connecting these vertices. Let D :

E ^ R + be a function that characterizes the length of edges, and | E | = m. Enumerate edges of the graph G from 1 to m and compose a new graph G ‘ =< V ‘ , E ‘ > whose vertices V ‘ are numbers of edges of the graph G, i.e. V ‘ = { 1, 2,..., m } . The set of edges E ^′ includes edges between vertices from the set V ^′ , if these vertices are adjacent edges in the graph G.

Let us determine the time t (in seconds) from the beginning of the day. Suppose that we have the passenger trains schedule and shunting operations schedule. Also, suppose that we use, for example, an algorithm from [8] to obtain a priori information on traffic of the shunting locomotives that perform these shunting operations. In this case, we can a priori specify the function F _total : V ‘ x R + ^ { 0,1 } that characterizes the freeness of any edge of the graph G from the traffic at the instant time t:

F total (j,t) =

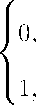
if the j-th edge (of the graph G)

is free from the traffic at the instant time t, otherwise.

Let the station be crossed by P passenger/freight trains during the day under consideration. Enumerate the trains in order of arrival at the station. For each of the trains, we can a priori set the function Fp : V‘ x R+ ^ {0,1} that characterizes occupation of any edge of the graph G by p-th train at the instant time t:

{ 0                if the j-th edge (of the graph G)

• 0,    is not occupied by the p-th train at the instant time t,

• 1,    otherwise.

2.    Problem Statement and Solution to the Problem

• 2.1.    Searching for Time Interval with Maximum Length During Which All Track Sections to Be Repaired Are Vacant Simultaneously

Note that                            _P

V j G V ‘ V t ^ F p (j,t) <  F total (j,t).

p=1

Consider the problem on track possession assignment. The problem is to determine the time interval during which a certain set of edges J = { j 1 ,..., j k ,... ,j _K } , where j k G V ‘ , is closed for traffic to provide technological works.

At the beginning, we consider the case of searching for the time interval (t * , t 2 ) with maximum length A _max = = t 2 — t 1 during which all track sections (edges) included in the set J are free from the traffic. In this case, the condition

F total (j k ,t)=0 V t G (t 1 ,t 2 ) must be satisfied V j k G J . This condition can be rewritten as ^t 2 ^∗

У F total (j k ,t)dt = 0. ^∗ t ₁

The problem on searching for the desired interval is

t ₂ — t 1 ^ max t 1 ,t 2

with respect to t2

^jk G J I F totai (j k , t)dt = 0,                              (2)

t 1

0 <  t 1 <  t ₂ <  86400 seconds,                            (3)

where 86400 is the number of seconds in day.

Note that solution to problem (1) with respect to (2) – (3) may not exist. This case is possible, when there is no time interval in which all edges are simultaneously vacant. If the solution to problem (1) with respect to (2) – (3) exists, then t ^∗ ₁ and t ^∗ ₂ are determined as the solution to this problem. However, problem (1) with respect to (2) – (3) is nonlinear programming problem. Therefore, there is complexity in obtaining solution. We introduce integer variables in order to reduce this problem to the mixed integer programming problem.

To this end, we use the function F _total (j, t) in order to form the set T _k consisted of the left and right boundaries of time intervals during which the j k -th edge is free from the traffic, k = 1, K.

With the help of the set Tk , we can determine the time intervals in which jk-th edge is vacant. Arrange elements of the set Tk in ascending order and form the vector τk . Suppose that dim Tk = 2Ik, where Ik is the number of such intervals.

Introduce the new variable dk that is equal to 1, if the time interval [t1,t2] is entirely inside [т^-1,т2] for the jk-th edge, and is equal to 0 otherwise, k = 1,K, i = 1,Ik. In terms of the new variables δki , problem (1) with respect to (2)-(3) is reduced to the problem t2 —11 ^ max(4)

t1 ,t2 ,δ11 ,...,δ11 ,...,δK1 ,...,δK with respect to

£ di = 1,k = 1K, i=1

t2 < dit^ + (1 — di)86400, k = T?K, i = Vk, ti > dit^-1 ,k = 1,K,i = 1,Ik, di G {0,1},k =1,K,i = 1,Ik, t1 ≤ t2.

For each edge included in the set J, conditions (5) – (7) guarantee that the time interval (t 1 , t ₂ ) is entirely inside one of the time intervals, when this edge is free from the traffic. At the same time, upper and lower bounds of track possession does not exceed bounds of the day under consideration.

• 2.2.    Searching for Time Interval with Duration That Is Not Less Than the Specified One in Which the Number of Occupied Track Sections to Be Repaired Is Minimal

As a rule, either the time interval (ti, t2) is insufficient in terms of its length or the track possession should be assigned at the time in which edges from the set J are occupied. Therefore, in order to assign track possession, it is necessary to transfer the traffic to other tracks (edges). To this end, consider the problem of searching for the time interval (t1, Й;) with duration that is not less than A in which the traffic has the minimal intensity. Here by intensity we understand the total (for all edges) number of time intervals when these edges are occupied inside suggested track possession.

If some subset of edges from the set J is free from the traffic in the day under consideration, then remove this subset from the set J and form the new set J . Suppose that this set contains K edges and J = { j (₁) ,..., j ( _k ) ,... ,j (K) } .

We use the function Ftotal (j, t) in order to form the set Tk consisted of the left and right boundaries of the time intervals in which the j(k)-th edge is occupied by trains, k = 1, K. With the help of the set Tk, we can determine the time intervals in which the j(k)-th edge is occupied. Arrange elements of the set Tk in ascending order and form the vector Tk. Suppose that Zs dim Tk = 2Ik, where Ik is the number of the time intervals, where the j(k)-th edge is occupied.

Introduce the new variable 5 " that is equal to 0, if the intersection of the time interval [t ₁ ,t ₂ ] with the interval [T ^{2 - 1} , T_k ^k ] consists of the single point as maximum, and is equal to 1 otherwise, k = 1,K, i = 1,I _k . If the variable 5 " is equal to 1, then it is necessary to transfer the traffic from the j (_k) -th edge at the interval [t^i ^{- 1} , т_к ^г ] in the suggested track possession. If the variable 5 " is equal to 0, then either t ₁ >  t 2ⁱ or t ₂ <  t _k i ^{- 1} . Therefore, we introduce the auxiliary variables y " , $ " . The variable y " is equal to 0, if t ₁ >  t 2i , and is equal to 1 otherwise. The variable $ " is equal to 0, if t ₂ <  т^{2г - 1} , and is equal to 1 otherwise. Note that the variable 5 " is equal to 1, only if y " = $ " = 1. In terms of the variables y " , $ " , we obtain the following form of the problem on searching for time interval with duration that is not less than the specified one in which the number of occupied track sections to be repaired is minimal:

K I k

EEfk^   .i i min_(10)

"1 i=1          t1,t2,^k,Yk,^k, " 1,K, i ^Ik t2 - t1 > A, t1 > (1 - y" )fk2i ,k = EK ,i = T!k,  (12)

t2 < (1 — $kvt^ ' + 86400$", k = 1,K, i = 1, I", fk > y"   $ - 1, k = EK,i = Uk,

^ G {0,1}, y" G {0,1}, $" G {0,1}, k = EK, i I".

Condition (11) guarantees that the length of the obtained time interval is not less than the preset parameter A. Conditions (12) - (13) are necessary to verify that the conditions t ₁ >  t ² and t ₂ <  t ^{2 - 1} are fulfilled. Taking into account conditions (15) and the form of the function to be optimized, we obtain that condition (14) guarantees that 5 " is equal to 0, if either $ " or y " is equal to 0. If both these variables are equal to 1, then 5 " is equal to 1.

Note that, in contrast to problem (4) with respect to (5) – (9), problem (10) with respect to (11) – (15) always has solutions. Also, problem (4) with respect to (5) – (9) and problem (10) with respect to (11) – (15) are inverse in some sense. In the first problem, the time interval is searched with the strict restriction that every considered edge must be vacant. In the second problem, the length of the interval is bounded, and some edges can be occupied inside this interval. At the same time, the solution to problem (10) with respect to (11) - (15) is meaningful only when A max < A.

Note that problem (10) with respect to (11) – (15) can have several solutions. Therefore, from all solutions to this problem, we choose the best solution in terms of maximum length of the time interval in which we need to transfer the traffic from edges that belong to the set J only f ^∗ times, where f ^∗ is an optimal value of the criterion in problem (10) with respect to (11) – (15). Therefore, the potential track possession can be increased, and there is no additional transfer of the traffic.

To this end, we need to solve the problem t2 — t1 ^        max__ __(16)

tl,t2,

K I k

ЁЕ = f.

k=1 i=1

Therefore, we have the solution to problem (16) with respect to (11) – (15), (17) and can set the desired t 1 and t 2 .

• 2.3.    Searching for Time Interval with Duration That Is Not Less Than Specified One in Which Number of Delayed (Postponed) Passenger/Freight Trains Going Through Track to Be Repaired Is Minimal

There can be another sense of traffic intensity. The intensity can be understood as the number of passenger/freight trains to be either transferred to neighboring free routes or simply accepted later due to track possession assignment. In this regard, we consider the problem of searching for the time interval (t1, t2) with duration that is not less than A in which the preassigned set of edges J = {j,..., jk,... ,jK}, where jk E V‘ is occupied by the minimum number of passenger/freight trains. If trains do not occupy some edges from the set J, we exclude these edges from consideration and renumber the remaining edges according to the order of arrival at the station. Suppose that P > 1 trains remain after such exclusion. Introduce the new variable δp that is equal to 0, if the p-th passenger/freight train is not transferred or delayed, and is equal to 1 otherwise. For the p-th train we consider only such edges from the traffic route at the station that belong to the set J, and exclude from consideration the remaining edges. Suppose that, after exclusion of such edges, Kp items remain. Compose the new set Jp = { j^,..., jp),..., jp^, )} from the remaining edges. For each edge that belongs to Jp, we use the function Fp(j,t) in order to form the set Tp,k consisted of the left and right boundaries of the time intervals when the jpk)-th edge is occupied by the p-th train, p = 1, P, k = 1, Kp. With the help of the set Tp,k, we can determine time intervals in which the j(k)-th edge is occupied by the p-th train. Arrange elements of the set Tp,k in ascending order and form the vector Tp,k. Suppose that dim Tp,k = 2Ip,k, where Ip,k is the number of such intervals.

Introduce the new variable δ _p ⁱ _,k that is equal to 0, if the intersection of the time interval [t ₁ , t ₂ ] with the interval [Tp ik - ¹ , Tp ik ] consists of the single point as maximum, and is equal to 1 otherwise, p = 1, P, k = 1, K _p , i = 1, I _p,_k . If the variable d p _k is equal to 1, then the p-th train should be transferred or delayed. The variable d p _k is equal to 0, if either t ₁ >  Tpik or t ₂ <  Tpik - ¹ . Therefore, we introduce the additional variables Y _pk , ^ p_k • The variable y _p- is equal to 0, if t ₁ >  Tpik , and is equal to 1 otherwise. The variable $ p _k is equal to 0, if t ₂ <  T pik - ¹ , and is equal to 1 otherwise. Note that the variable d p _k is equal to 1, only if Y k _p = ® k _p = 1. In terms of the introduced variables, we obtain the following form of the problem on searching for the time interval (t 1 ,t 2 ) with duration that is not less than A in which the preassigned set of edges J = { jd,... , j _k ,... ,j _K } , where j _k E V ‘ is occupied with the minimal number of passenger/freight trains:

P

^2 dp ^             min    (18)

.              ti,t2, ^,Si , ,Yi , ,$i , ,p—1,P, k=1,K, i=1,U p—1             1, 2, p, pk 'p,k’ p,k,r ’ ’      , p ’’ t2 -11 > A, _____  (19)

t1 > (1 - Yp,k)T^k, P = 1,P,k ^Kp, i= 1,Ip,k,  (20)

t2 < (1 - ^.-.■ + 86400$p,k ,p = 1, P ,k = 1, Kp, i = 1, Ipk, dp,k > Yp,k + ®p,k — 1, p = 1, P, k = 1, KP, i = 1, IP,k,

K p I p,k ^δ pⁱ,k

5p > k-1---,p =1,P,

K p

Ip,k k=1

dp E {0,1}, dp,k E {0,1}, Yp,k E {0,1}, ^p- E {0,1}, p = 1, P, k = 1, Kp, i = 1, Ipk.

Conditions (23) are the main conditions in problem (18) with respect to (19) – (24). These conditions are necessary in order to determine whether the p-th train should be transferred. First of all, note that                  _ -           _

K p ^I p,k          K p

0 <  Eip.k • k =1 i =1         k =1

At the same time, if at least one edge included in the set of edges J from the route of a passenger/freight train is occupied at the time interval (t1,t2), then at least one variable δi k is equal to 1. Consequently, p’                                                      - - p p,k

δpi,k dp > k—4^—1— > 0.

^P"   K p

S IP,k k—1

Therefore, taking into account conditions (24), we have that d _p = 1. Conditions (20) - (22) are similar to conditions (12) – (14) with only difference that conditions (20) – (22) point to freeness or occupation by individual train at the time interval (t ₁ , t ₂ ), while conditions (12) – (14) point to freeness or occupation by all trains going through the station at the time interval (t ₁ , t ₂ ).

Note that problem (18) with respect to (19) – (24) can have several solutions. Therefore, from all solutions to this problem, we choose the best solution in terms of maximum length of the time interval at which we need to change the route only for f∗ trains, where f∗ is an optimal value of the criterion in problem (18) with respect to (19) – (24). To this end, we need to solve the problem t2 — t1 ^              max__ ___ ___ (25)

ti ,t2,5p,8'i,k ,Yp,k ,$p,k ,p=1,P,k=1,Kp,i=1,Ip,k with respect to (19) – (24) and the additional condition

P

5 p = f * .                                       (26)

p= ¹

Therefore, we have the solution to problem (25) with respect to (19) – (24), (26) and can set the desired t 1 and t ^ .

3.    Example

Consider some set of edges to be closed for the repair at the station with the part given in Figure. Suppose that these edges are occupied according to Table 1.

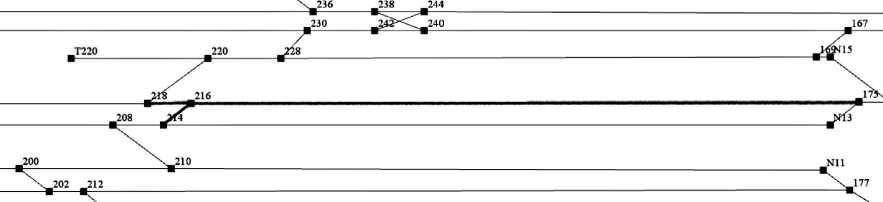
Scheme of the part of the station with track sections (edges) to be repaired marked by bold font

Table 1

Edges occupation time by trains

Edge			Occupation edge
	From-till	No.	From-till	No.	From-till	No.
	2283-2327	331	19743-19787	59	25503-25547	455
	30339-30778		33360-33389		34224-34266	360
216 ↔ 218	34328-34357		37884-37926	478	41314-41343
	43983-44027	399	50004-50046	130	55973-56015	241
	66783-66827 81352-81381	87	72783-72827	97	81293-81322
	30088-30127	122	31021-31049		33333-33360
	34300-34328		34950-34977		35221-35248
214 ↔ 216	41287-41314		41387-41414		48259-50698
	50941-50969		68053-70978		71221-71249
	74564-74591		75412-75439		83775-83802
	83-2283	331	16343-19743	59	22858-22979
	22980-25503	455	30127-33639	122	34266-36939	360
216 ↔ 175	37926-40500	478	41414-41658		41783-43983	399
	50046-52599	130	53663-55973	241	63983-66783	87
	68480-72783	97	74591-74835		75168-75412
	81049-81293		81381-83268		83531-83775

In Table 1, the column “No.” gives the number of the passenger/freight train that occupy the edge pointed in the column “Edge” at the time interval given in the column “From-till”. If a row in the column “No.” is empty, then the edge is not occupied by a passenger/freight train, but, for example, is occupied by a shunting locomotive.

Taking into account the data shown in Table 1, we have that the solution to problem (4) with respect to conditions (5) - (9) is t ; = 2327 and t 2 = 16343.

Now we analyze solutions to other stated problems depending on parameter A.

It follows from Table 2

that the optimal time intervals generated by problem (16) with respect to (11) – (15), (17) and problem (25) with respect to (19) – (24), (26) can be different, but also can overlap. In this case, we expect that increase in the parameter A leads to increase in the optimal values of the corresponding criterial functions.

Optimal time intervals for track possession assignment

Table 2

A	f ∗	(t ; ,t 2 )	f ∗	(t ; ,%)
18000	2	(2327, 22858)	1	(2327, 22980)
21600	4	(2327, 25503)	2	(56015, 86400)
36000	16	(44027,81049)	4	(44027,86400)
43200	24	(41658,86400)	5	(40500, 86400)

Conclusion

We investigate the problem on track possession assignment at the station taking into account the current schedule. In order to assign track possession, we consider different problems and solve the problems by methods of mixed integer linear programming. First, we solve the problem on searching for the time interval with maximum length during which all track sections to be repaired are vacant simultaneously. If the duration of such interval is insufficient, then we propose and solve the problem on searching for the time interval with duration that is not less than a predetermined one in which the number of occupied track sections to be repaired is minimal. If there is detailed information on trains going through track sections to be repaired, then in order to assign track possession, we solve the problem of searching for the time interval with duration that is not less than the specified one at which the number of delayed (transferred) passenger/freight trains going through track sections to be repaired is minimal.

Acknowledgements. This paper was performed in a framework of government assignment of the Ministry of Education and Science (project no. 2.2461.2017/Pch).