One approach for extrapolation of rock mass parameters in tunneling

This article describes a methodology that shows how it is possible to integrate all these approaches in a problem for extrapolation of the parameters for hydrotechical tunnels.

During the design process for tunnels in hydrotechics, one of the main problems is how to extrapolate the deformability and shear strength rock mass parameters from the zone of testing to the whole area (volume) of interest for interaction analyses between structure abd natural environments. Computers development in recent decades has contributed to the development of numerical calculation method in rock mechanics which enabled new and wider possibilities of stress and deformation calculation. This had significantly stimulated the development of rock mechanics and tunneling as scientific and technical discipline as well as the wider application of research results into practice [1-17].

Short review of the literature

The extrapolation procedures are innitally developed for design problems at large dams by Kujundžić [2], [5], but later is constantly expanded oby Lokin and Čolić 1980, 1990 and 1996; Lokin, Lapčević, Petričević, (1989); Čolić, Manojlović, (1983); Jovanovski, Gapkovski, 1998; Jovanovski et al., (2000); Jovanovski, Gapkovski, Ilijovski, (2002,  2003, 2004); Ilijovski, Jovanovski, Velevski, (2004); Ilijovski, (2005) etc.

Contribution to defining deformability and shear strength of rock massif through empirical failure criteria is given by Hoek and Brown, (1980, 1983, 1988).

Classification systems developed in the field of rock mechanics that need to be highlighted are Geomechanical Classification – Rock Mass Rating system (Bieniawski, 1970, 1973, 1974, 1975,

1976, 1979, 1989); RSR - Rock Structure Rating (Wickham, Tiedemam and Skinner, 1972, 1974); Q system - Rock Mass Quality (Barton, Lien and Lunde, 1974).

Methods of analysis

Limitations in a process of investigation in rock masses comes from the fact that the whole tunnel length cannot be completely covered with detailed geological and geotechnical investigations. So, it is necessary to find a way to extrapolate the necessary parameters from smaller volume of testing zone to the whole volume of the rock mass along the tunnel length.

The given approach in a frame of this article can be defined as Empirical–Static-Dynamic (ESD) methodology of extrapolation. The prerequisite for using this methodology is following:

• -    to have enough data for reliable rock mass classification.

• -    to have enough testing data for deformability with static tests.

• -    whole structural zone (in this case tunnel) to be covered with geophysical seismic tests.

Such testing must be performed in a manner that will insure reliable data for geotechnical modeling of the whole area along the tunnel length.

One of the key problems here is to divide tunnel length in so called quasi-homogenous zones with relative uniformity of the deformability and shear strength rock mass properties as basic and constitutive elements of geological model.

Inside such zone some conditions or properties are the similar in every point, and very different outside it. Each and every zone is determined by space limits and consists, in some way, properties which are important for the study.

It shall be noted, that the process of extrapolation is strictly connected and interrelated to the process of geotechnical modelling of the terrain. The complex geotechnical model is consisted of three basic models (Pavlović, 1995, 1996):

• -    model of natural geological environment; ’

• -   model of engineering activity - geotechnical model in narrow sense (GM);

• -   model of interaction - model of stress-strain behavior.

A flowing-chart which shows the connections between each model is presented in figure 1.

Geological model (Geological profiles, EG sections)

Engineering - geological model with separeted quasy-homogenous zones

Model of engineering activity

Model of interaction - model of stress-strain behavior

• Figure 1. Steps for connection between different models

It can be underlined that the model of engineering activity and the model of interaction are final phases of geotechnical modelling.

Results

To illustrate the methodology, one example is shown for the hydro technical tunnel constructed for the area of arch dam “Sveta Petka” on a river Treska in Republic Macedonia (Fig. 2, Tab. 1).

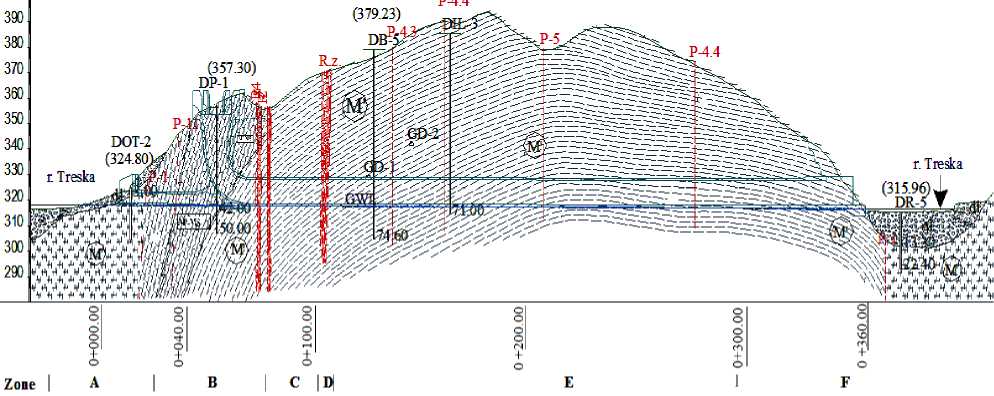
Figure 2. Engineering Geological Section for hydro technical tunnel for arch dam "Sveta Petka" in Republic of Macedonia

In the Figure 2 the following notation:

M- marbles; M’-foliated marbles; al-alluvial deposits; GWL-groundwater level; DP-1-boreholes; GD-investigation galleries; Rz-fault zones; P-faults; D-deformation modulus; E-elasticity modulus; Vp-value of longitudinal seismic waves defined with geophysical tests; Q-value of rock mass quality after Barton et all; RMR-Rock Mass Rating after Bieniawski.

Table 1. Hydro technical tunnel for arch dam "Sveta Petka"

Zone	Deformation modulus, D [MPa]	Elasticity modulus E [MPa]	Value of longitudinal seismic waves defined with geophysical tests, Vp [m/s]	Value of rock mass quality after Barton et all, Q	Rock    Mass Rating    after Bieniawski, RMR
A	3900-4500	8900-12000	4000-4600	1.46	49
B	4900-5800	11000-14000	4600-4700	1.58	52-56
C	4900	11000	4700	1.80	54
D	700-800	1600-1700	2600	0.40	21-25
E	6500-7500	15000-17000	4800-5000	1.66-2.0	57
F	3200-3500	7000-8000	3600	1.33	48

To define this Engineering-Geological Section, the following methodology of investigations is used:

• 1.    Collection of data for rock massif test results, particularly laboratory and field test results of strength, deformation, discontinuities and other parameters.

• 2.    Specific laboratory and field testing for a specific purposes.

• 3.    Statistical analysis of the tested parameters.

After that, all of the results from geological, geotechnical and geophysical investigations were used for establishing physical model through the RMR, Q and GSI classification.

Correlations between the quality of rock massif (RMR, GSI and Q indexes), dynamic (Vp) and static properties (D and E) of rock masses are expressed using results of the detailed classification of the rock massif around the measuring point with dilatometer testing’s.

Typical deformability diagrams from dilatometer tests are given in figure 3.

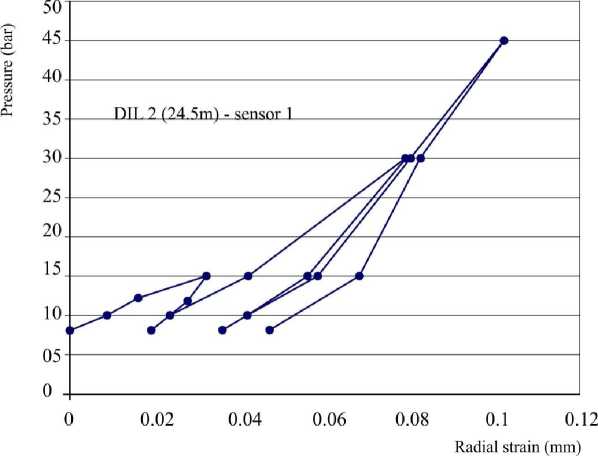
Figure 3. Typical diagram from dilatometer testing for a Rock Mass with low rating (RMR=20-25)

Diagrams shown on Figure 3 are basic for estimating of deformation modulus and elasticity modulus and imply not only to its' value than also to dependence of the modulus on pressure itself, so the point is rock mass „strengthening“ or „softening“ regarding to pressure.

Based on detail analyses, a numerous regression models are obtained in order to fulfill the necessary criteria for extrapolation. Here, several type of regression models can be used. For example, some regressive dependences between quality of rock mass RMR and velocities of longitudinal elastic waves v and deformation modulus (D) for several locations (between them for dam „Sveta Petka” is presented in figure 4 and figure 5.

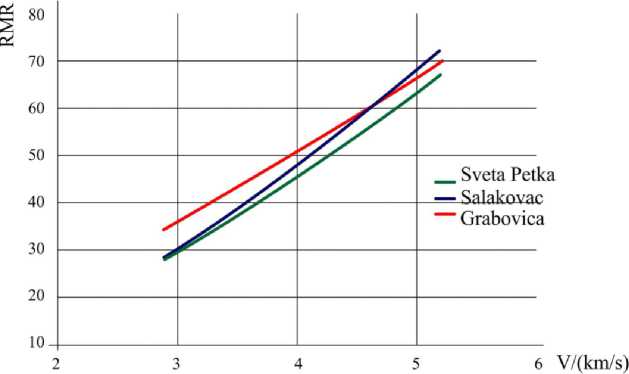
Figure 4. Regression curves between quality of rock mass RMR and velocities of longitudinal elastic waves v_l from the location on “Salakovac” dam RMR =9.8519 xv l ^1.1721and „Grabovica” dam

RMR =9.4537 xvl ^1.2179 with correlative dependances fort the „Sveta Petka” dam RMR =5.6848 xvl ^1.4979

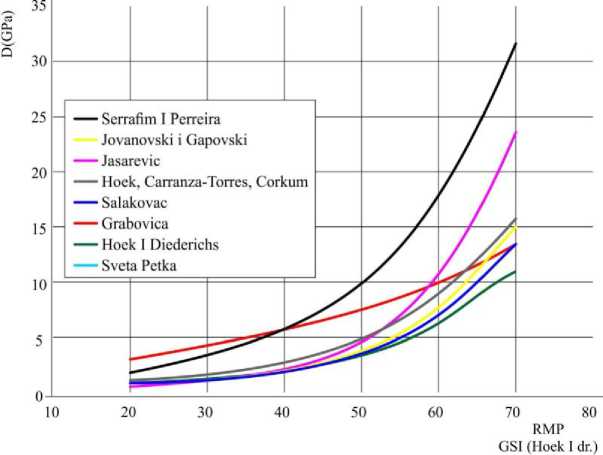
Figure 5. Correlative dependences between quality of rock mass RMR (GSI) and deformation modulus D from the location on “Salakovac” dam D=0.1369 xe ^0.065RMR (GPa), „Grabovica” dam D=1.6963 xe ^0.0295RMR (GPa), and “Sveta

Petka” D=0.1104 xe ^0.0703RMR dam with known correlative dependences from literature [2, 5]

Advantage of analytical models showed in Figures 4 and 5, is that can make predictions and extrapolations relatively quickly and accurately and in that form is very appropriate for practical using. Whereat, when prediction of the parameters is made in this way, it needs to mention those different in situ tests are made with different levels of vertical stress, for different strengths, anisotropy and etc.

It is clear that if we combine empiric an field's methods, we can succesfully cover a lot of cases which are important for project analysis, but it is also clear that examples on the figures always have to be carefully used, reexamined and attentively engaged in geotechnical models.