One-bit Hard Combination Decision Scheme for Cooperative Spectrum Sensing in Cognitive Radio

Published Online October 2013 in MECS

In recent years, cognitive radio (CR) has emerged as a promising paradigm for exploiting the spectrum opportunity, which is restricted by the current rigid spectrum allocation scheme, to solve the spectrum scarcity problem [1]. One of the fundamental challenges in spectrum sensing is to reliably detect the primary users (PUs) signals. In CR terminology, primary user can be defined as the licensed user who has rights on the usage of a specific part of the spectrum. On the other hand, CR user sense the RF environment without causing interference to PUs, identify the available spectrum if PUs are absent and change its radio parameters to used the unoccupied spectrum. The fundamental task of CR users is to detect the presence of PUs through spectrum sensing. A number of different techniques have been proposed for identifying the presence of the PU. The existing spectrum sensing techniques can be broadly divided into three categories [2]: cyclostationary detection [2], matched filter detection [3] and energy detection [12]. Among them, energy detection has been widely applied since it does not require any a priori knowledge of the primary signals and has much lower complexity than the other two schemes. But spectrum sensing is a tough task because of shadowing, fading, and time-varying natures of wireless channels. To combat these impacts, cooperative spectrum sensing schemes have been proposed in [4-10] to obtain the spatial diversity in multiuser CR networks. In cooperative spectrum sensing, information from different CR users is combined to make a decision on the presence or absence of the primary user. Cooperation among CR user is usually coordinated by a fusion center through hard or soft decision fusion strategies. In hard decision technique the individual CR user makes the one-bit decision regarding the existence of the PU. The bit-1 indicates the presence of PUs. After observing the PU signal, the local detection forwards them to data fusion centre for further process. The final decision then is taken by combining all local detection based on OR. In the case of soft decision, the decision is taken by correlating the measurement made by individual users in signal detection. Conventional one-bit hard decision for cooperative spectrum sensing has been investigated in [9-11] and one-bit weighted hard combination for cooperative spectrum sensing proposed in [14]. This paper investigates the performance of 1-bit hard combination scheme for cooperative spectrum sensing in Cognitive Radio.

The rest of this letter is organized as follows. In section II signal processing techniques like matched filter, energy detector and cyclostationary method are discussed. System model is included in section III. One-bit Hard combination scheme with OR rule was discussed on section IV. Section V discusses the simulation result and finally conclusion is drawn in section V.

• II.    Spectrum Sensing Techniques

• 2.1    Matched Filter

• 2.2    Energy Detector Using Welch Periodogram

• 2.3    Cyclostationary Feature Detection

In this section we discuss three techniques that are matched filter, energy detector and cyclostationary feature detector.

The optimal way for any signal detection is a matched filter [15], since it maximizes received signal-to-noise ratio. However, a matched filter effectively requires demodulation of a primary user signal. This means that cognitive radio has a priori knowledge of primary user signal at both PHY and MAC layers, e.g. modulation type and order, pulse shaping, packet format. Such information might be pre-stored in CR memory, but the cumbersome part is that for demodulation it has to achieve coherency with primary user signal by performing timing and carrier synchronization, even channel equalization. This is still possible since most primary users have pilots, preambles, synchronization words or spreading codes that can be used for coherent detection. However, a significant drawback of a matched filter is that a cognitive radio would need a dedicated receiver for every primary user class.

Averaging

One approach to simplify matched filtering approach is to perform non-coherent detection through energy detection. This sub-optimal technique has been extensively used in radiometry. An energy detector can be implemented similar to a spectrum analyzer by averaging frequency bins of a Fast Fourier Transform (FFT), as outlined in Figure 1. Processing gain is proportional to FFT size N and observation/averaging time T. Increasing N improves frequency resolution which helps narrowband signal detection. Also, longer averaging time reduces the noise power thus improves SNR. However, due to non-coherent processing O(1/SNR2) samples are required to meet a probability of detection constraint. There are several drawbacks of energy detectors that might diminish their simplicity in implementation.

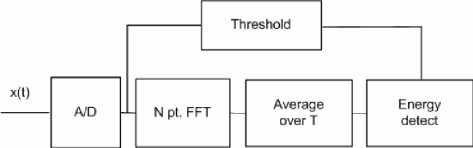
Fig. 1: Implementation of an energy detector using Welch periodogram averaging

Modulated signals are in general coupled with sine wave carriers, pulse trains, repeating spreading, hoping sequences, or cyclic prefixes which result in built-in periodicity. Even though the data is a stationary random process, these modulated signals are characterized as cyclostationary , since their statistics, mean and autocorrelation, exhibit periodicity. This periodicity is typically introduced intentionally in the signal format so that a receiver can exploit it for: parameter estimation such as carrier phase, pulse timing, or direction of arrival. This can then be used for detection of a random signal with a particular modulation type in a background of noise and other modulated signals. Common analysis of stationary random signals is based on autocorrelation function and power spectral density. On the other hand, cyclostationary signals exhibit correlation between widely separated spectral components due to spectral redundancy caused by periodicity [16].

• III.    System Models

The energy detector consists of a square law device followed by a finite time integrator (fig.-2). The noise pre-filter serves to limit the noise bandwidth and to select the bandwidth of interest. The noise at the input to the squaring device has a band-limited, flat spectral density [12]. The output of the integrator at any time is the energy of the input to the squaring device over the interval T in the past.

Squaring

Device     Integrator

= ¹ J y ^{2 (} r ) d

T t = T

Fig. 2: Energy Detection

Finally, this output signal Y is compared to the threshold in order to decide whether a signal is present or not. The threshold is set according to statistical properties of the output Y when only noise is present.

Consider a CR network with N cooperative users and M samples are utilized. The energy detection [12] [13] is applied at each CR user. The received signal at the i th sample of the j th CR user r ji , 1 ≤ j≤ N, 1 ≤ i≤ M , is given by

Where u= time bandwidth factor and pQ Г ( '.' ) Y

Q denote the gamma function, upper incomplete gamma function, signal to noise ratio (SNR) and generalized Marcum’s Q function respectively.

j 1 Yv n *, H i

where Y s denotes the received primary signal with the average power % and n , denotes the white noise. In (1), H 0 and H 1 denote the hypotheses corresponding to the absence and presence of the primary signal respectively. The goal of energy detection is to decide between the two hypotheses. The received signal r ji is Gaussian with [14],

IV. One-bit Hard Combination Scheme

In the conventional one-bit hard combination scheme, there is only one threshold dividing the whole range of the observed energy into two regions. As a result, all of the CR users above this threshold are allocated the same weight regardless of the possible significant differences in their observed energies. Intuitively, a better detection performance can be achieved if we divide the whole range of the observed energy into more regions, and allocate larger weights to the upper regions and smaller weights to the lower regions.

Г ji

H 0

H 1

According to (2), the observed energy in at the j th CR user is given by [14]

Energy ( Y ) * 7		Region 2,	^ 2   2
2 I 1		Region 1,	^ =	1
		Region 0,	® 0 =	0

Fig.3: Principle of 1-bit hard combination scheme

M i=1

^bj 0,

^H 1^,

where random variables b j ₀ and b j ₁ follow a central chisquare distribution with M degrees of freedom. Let x be the local decision threshold for each CR user, then the local false alarm probability P f and detection probability P f can be obtained from (3) as,

Fig. 3 shows the principle of one-bit hard combination scheme. Different from the conventional one-bit scheme with only one threshold, two thresholds [14] in one-bit scheme I and I are adopted to divide the whole range of the decision statistic of the local spectrum sensing into three regions. In the fusion center, if the energy value falls into the corresponding region, it will be judged as "1", no information or "0". This decision criterion is equivalent to allocating the 3 regions different weights to ₀ = 0, to 1 = 1, to ₂ = 2 and the weighted summation is given by

^Nc = ^N 2 - ^ 2 ^{+ N} 1. - ^ 1              (6)

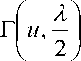
r(u )

where N₁ is the number of local detectors the energies of which are greater than X 1 and less than X ₂ , N 2 is the number of local detectors the energies of which are greater than I ₂ . The decision rule [15] adopted is given by

D =

'1

N ^ 1

otherwise

Each CR user needs to feedback one bit information to indicate which region its observed energy falls in. The primary signal will be declared present if any one of the observed energies falls in region 2, or one of them fall in region 1. In this criterion, while determining the threshold, probability of false alarm P fa is fixed to some value and the probability of detection P_d is maximized. Table 1 shows the P f _a values chosen for determining the two thresholds.

Table 1: Threshold and the corresponding false alarm values in the 1-bit hard combination scheme

Threshold	False Alarm Value
i 2	в 2 P a
i 1	P fa

The coefficients P_n in Table 1 are found by

P . = ( n - 1 ) x 10 ^{-( n - 1} > , n = 2          (8)

where n is the threshold index and в = 1 ■

For the 1-bit hard combination scheme, thresholds X 1 and i ₂ need to be determined to meet the target overall false alarm probability of the N -user CR network Q F exactly, and also to optimize the detection performance.

Table 2: Energy regions and corresponding weights in the 1-bit hard combination scheme

Region	Weight
2	w2 = 2
1	w 1 = 1
0	w o = 0

Weights shown in Table 2 are determined in the following manner. If 50% of all CR users observe energy in Region 2, with no observed energies in other regions, or 100% of all Cognitive Radio Users observe energy in Region 1 with no observed energies in other regions, the signal of interest is said to be present. Table 2 summarizes the percentage of CR users required in a given region to declare the presence of the signal of interest, with no observed energies in other regions. While other percentage values are possible, the chosen values in Table 3 provided satisfactory results.

Table 3: Design for determining the weights of the 1-bit hard combination scheme

Region	Required number of Cognitive Users to declare the presence of signal of interest in a given region with no observed energies in other regions
2	50% of all Cognitive Users
1	100% of all Cognitive Users
0	-

Let Q be the probability that one or more observation local energy values are greater than i and Q be the probability that more than N = ^ 1/ to_x J observation local energy values are greater than i and less than i . We have [15]

where P is the probability that the local energy value is greater than i and according to (5)

P„ = P ( S 0 >  i ) =

Q , 2 = 1 - PN 2 = 0| H 0 ) = 1 - ( 1 - P f 2 ) N  (9)

Q, 1 = P ( N 2 = 0| H о ) . f> ( N 1 = pH о )

J = N

N

= ( 1 ^{- P}, 2 )

N

. к N ( P , 1 - P , 2 ) . ( 1 - P , 1 + P , 2 ) ” J

_ j = n 1 V j 7                                          ,

г ( M in- 7

V 2 ^, 2 7

M

i n

= 2 Г^{- 1}

M ^{, p} ,n ^rt M У ²       V ² 77

M

Г ^{- 1} (,) denotes the inverse of the incomplete gamma function. Then the probability of false alarm in the fusion center can be expressed as

Q , = Q , 1 + Q , 2                   (13)

Suppose all the channels between the primary user and secondary users are independent identically distributed. The probability of detection [15] in the fusion center can be expressed where Pdn is the probability that the local energy value is greater than ^ .

Qd = 1 -(1 - Pd 2 ) N +(1 - Pd 2 ) N

N

"Z j = Ni

( N

( P , - P.y . (i - P . + p,₂ ) N - ^j d 1       d 2     .          d 1       d 2

V. Simulation Result

All simulation was done on MATLAB version R2011a under AWGN channel by taking time bandwidth factor u =1000 and the probability of false alarm is used from 0.01 to 1. The number of samples adopted are M =2000. “OR” rule is employed for one-bit hard combination scheme.

1-bit Hard Combination scheme with Convensional OR rule under AWGN

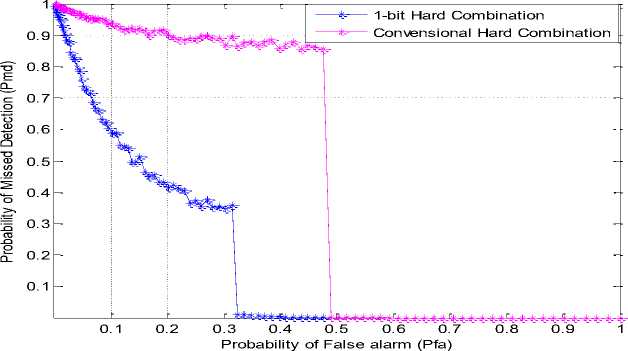
Fig. 4: Complementary ROC of conventional and one-bit OR rule

Fig. 4 shows complementary ROC of conventional OR rule and one-bit OR rule in the hard combination scheme. Where 10 CR users and SNR=15dB were taken for simulation. It shows that probability of missed detection in one-bit hard combination scheme is reduced significantly than the conventional hard combination scheme. One-bit hard combination scheme gives much better performance than the conventional one-bit scheme.

1-bit Hard Combination scheme with

0.9

0.8

0.7

0.6

0.5

0.4

0.3

0.2

0.1

0.1    0.2    0.3    0.4    0.5    0.6    0.7    0.8    0.9     1

Probability of False alarm (Pfa)

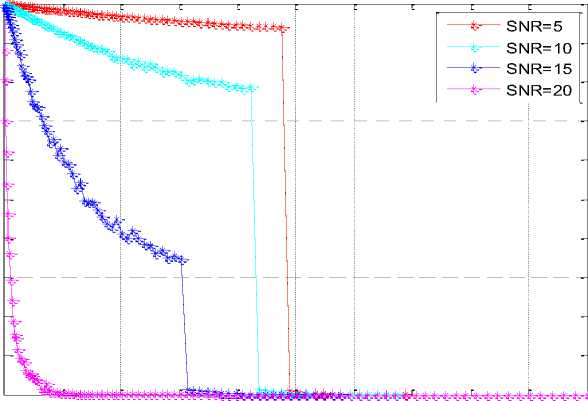
Fig. 5 shows complementary ROC of one-bit hard combination scheme. Where 10 CR users and SNR=5dB, 10dB, 15dB and 20dB were taken for simulation. It shows that the probability of missed detection decreases based on the increased on SNR. So SNR influences on the detection probability.

1-bit Hard Combination scheme with different CR Users under AWGN

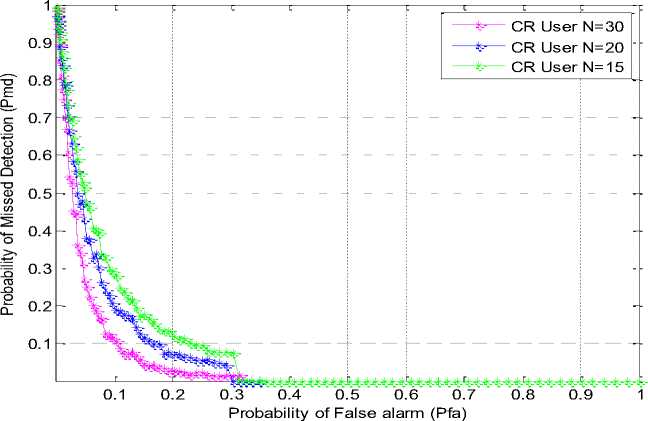
Fig. 6: Complementary ROC of 1-bit OR rule with different CR users

Fig. 6 shows complementary ROC of one-bit hard combination scheme for different number of user N=15, 20 and 30 and SNR =15dB. We observed that detection performance increases by increasing CR user.

• VI. Conclusion

Simulation result shows that the probability of missed detection is decreasing for both conventional hard combination and one-bit hard combination scheme with OR rule correspondingly with increasing the probability of false alarm. It is shown that one-bit scheme has much better performance than the conventional hard combination scheme. The probability of missed detection is decreased based on the increasing of CR users. The one-bit hard combination scheme exhibits much better performance than the conventional scheme.