One property of the weak covergence of operators iterations in von Neumann algebras

Conditions are given for *-weak convergence of iterations for an ultraweak continuous fuctional in von Neumann algebra to imply norm convergence.

Let M be a. von Neumann algebra. [5], acting on a separable Hilbert space H. Let T be a. contraction from M* to M*, so that TM*^ C M*. . On the pre-conjugate to M space M* there are two topologies selected: the weak, or the о^М*,М^ topology, and the strong topology of the convergence in the norm of the space M*.

Let now T = a*, where a be an automorphism of the algebra. AL. We will say that T in M* is mixing, if for all ж G M* and A G M, the following condition is valid:

lim Дпх,А) = 0, П^-СХЭ where

M^ = ^_ЕМ*-. y(l) = 0}.

We will say that a. positive contraction T in M, is completely mixing, if for all ж G M* the following condition is valid:

lim \\ТД\\ = 0.

П^-СХЭ

The following theorem is valid:

Theorem. Let T be a. pre-conjugate operator to an automorphism a of a. von Neumann algebra M for which there is no invariant normal state. Then, for x G M„ the weak convergence of Tⁿx implies the strong convergence of Tⁿx. In particular, if T is mixing, then T is completely mixing.

< Let us denote by \Tⁿx\ the sum

ДпхД + ^хД, where Tnx = ДпхД - ^хД is the Hahn decomposition of the functional Tnx [4]. The sequence {|Тпж|}”=1 is cr(AL*,AL) pre-compact [4] and, therefore, the convex envelope of the set {|Тпж|}^=1 is pre-compact as well. The sequence (An ж|}^х is also pre-compact because it belongs to the convex envelope of the set {IT"^}”,.

Because T is pre-conjugate to an automorphism, then \T x\ = T ж|. In fact, the support of Tg4_t is orthogonal to the support of HTW, ТП"^* - ТП"П- = ПТ"П = T ^+vx, and from the uniqueness of the Hahn decomposition [4] it follows that \T x\ = T ж|.

Weak Convergence Of Iterations In von Neumann Algebras

Let ж be o(M_t, M )-limit point of the set {А™ ж|}^₌₁. Then the functional ж will be T- invariant. In fact,

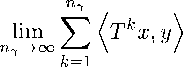
n7 — 1

= lim n”¹ • У (т^кх,у} - nV¹ • (ж, у) + п^¹ 71^—>ОО      ' ^Z ' \          /        '                     ¹

^х^

к=0

It is easy to see that ж > 0 and, therefore, from the conditions of the theorem it follows that ж = 0. Now we know that the only weakly limit point of the set {Aⁿ ж|}^₌₁ is the point ж = 0. Therefore

0= lim ||тГ|ж||| = lim (An ж|)(1) = lim (Tn |ж|)(1) = lim ||Т"|ж|||, 71—^00              П—^СХ)                 Tl^OQ                 Tl^OO because (Tn ж|)(1) = (Tm ж|)(1) for all n,m E N. The theorem is proven. >