Онтологическая система знаний и вычислительных ресурсов современных интеллектуальных технологий

Онтологическая система управления сложной системой разнородных знаний интегрирует формализованные знания классической и современной компьютерной математики [1], которые реализуются в нестационарной среде функциональных пространств современной теории катастроф (СТК) [2]. Концептуальный базис построения онтологической системы знаний в среде СТК определяет структурный синтез компонент эволюционирующей среды на базе активной динамической системы [3] (рисунок 1). Одна из особенностей онтологической системы знаний – иерархическая организация, определяющая функции интерпретации и управления в условиях временных задержек, шума и неопределённости.

Стратегическое планирование операций и концептуальных решений на основе онтологической системы в условиях иерархической организации системы знаний отображает фундаментальный результат интеграции компонент динамической модели СТК на базе интеллектуальных технологий и высокопроизводительных вычислений.

Иерархическая модель онтологии позволяет описывать эволюционную динамику сложной системы знаний на различных уровнях абстракции, определяющих функции интерпретации и управления в процессе развития текущей ситуации. При декомпозиции сложной системы реализуется концепция связности, при этом исходная модель знаний представляется совокупностью моделей подуровней, связанных древовидным отношением [4]. Формирование уровней иерархии осуществляется с помощью стандартных оснований декомпозиции.

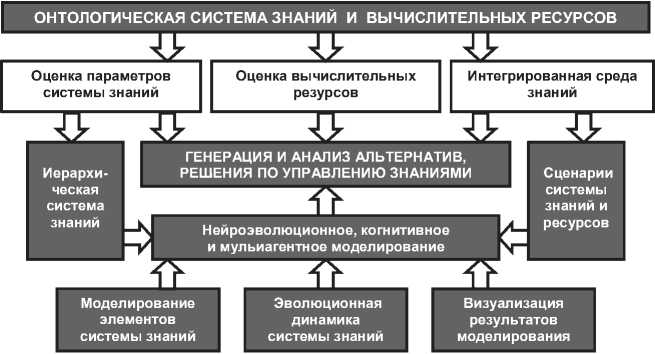
Рисунок 1 - Онтологическая система интегрированной среды интерпретации решений

1    Онтология сложной системы знаний

Концептуальная модель онтологии в функциональном пространстве знаний (рисунок 2) представлена на основе универсальной модели интерпретации сложных систем – динамической модели СТК [2]. Теоретические решения по реализации концептуальной модели онтологии базируются на фундаментальных результатах [1], сформулированных на основе требований минимальной длины описания А.Н. Колмогорова [5] в рамках теории сложности [6], принципа бифуркационного управления Н.Н. Моисеева [7], теории некорректных (обратных) задач А.Н. Тихонова [8].

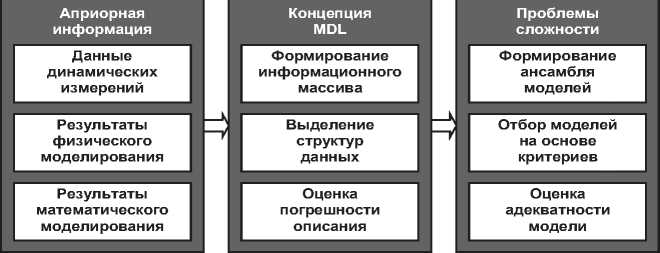
Рисунок 2 - Функциональное пространство онтологической системы знаний

Онтологическая база инструмента исследования использует методы оценки поведения сложной системы знаний на базе динамической модели CТК [2] – метод функционала действия [9], модифицированные модели Дуффинга и Матье, нелинейная диаграмма устойчивости Айнса-Стретта, когнитивная парадигма [1], мультиагентное моделирование [10].

Онтология эволюции сложной системы знаний, определяющая фундаментальные принципы и концепцию эволюционирующих систем, может быть представлена в виде определений и утверждений.

Определение 1 . Функциональное пространство эволюционной динамики рассматривается как совокупность предельных состояний, определяющих режимы движения к целевому аттрактору и при потере устойчивости:

• (1)    ^ 0 ^^ n “’^в >  Ж r ^^ ( F R , Attr ),

где ^ ° - исходная система состояния модели знаний; ^ ⁿ, ^ ^r - системы знаний в пространствах поведения и управления СТК; а и в - ограниченные операторы; ^ ( F R ,Attr ) - система знаний, определяющая формирование фрактальных и аттракторных структур [1, 2].

Определение 2 . Пространство поведения определяет множество состояний сложной системы знаний в виде алгоритмов идентификации, аппроксимации и прогноза в процессе эволюции в нестационарной среде на основе концептуальных решений, критериальных уравнений и нечёткой формальной системы:

• (2)    W ( t ° ь W ‘ ( t ) —^ W ( t ) - >■ W ( t „ ) ,

где W ( t₀ ) - исходная система множества состояний; W* ( t ) - факторизованная система, реализующая эволюцию знаний в пространстве поведения; W ( t i ) и W ( t_n ) - системы, построенные в результате использования интерпретирующих алгоритмов; а * - преобразование (гомеоморфизм), определяющее включение системы W* ( t ) в W ( t i ); в * - система канонических преобразований (гомоморфизмов) на интервале реализации [t ° , t_n].

Определение 3 . Пространство управления формируется на основе процедур построения сценариев развития эволюционной динамики с целью выработки управленческих решений в условиях неопределённости:

• (3)    W ** ( t ) — >  W **( t i ) - — > ... W * ( t _n ) ,

где W** ( t ) - множество, сформированное по результатам выполнения условий (1), (2); W **( t i ) - множество, определяющее пространство преобразований знаний (генерация альтернатив, построение ансамбля реализаций и выбор решения) при выработке управляющих воздействий; W *( t n ) - результирующее множество пространства управления в системе интеллектуальной поддержки (ИП); а ** - преобразование (гомеоморфизм), определяющее включение системы W **( t ) в W **( t i ); в ** - система канонических преобразований (гомоморфизмов) на интервале реализации [t ° , t n ].

Критерием целостности функциональной полноты модели знаний служит принцип неопределённости - дополнительности - совместимости, что демонстрирует свойство функциональной отделимости пространства взаимодействия и используется при синтезе функции интерпретации, определяющей выбор решения среди генерируемых альтернатив.

2 Иерархическая среда онтологии сложной системы знаний

Кооперативный характер эволюционной динамики сложной системы знаний порождает способность к нарушению её симметрии. Дифференциация и специализация обеспечивают распределение функций подсистем, а интеграция подсистем приводит к возрастающей способности функциональных возможностей многофункционального программного комплекса (МПК). Иерархическое построение сложной системы ведётся в виде пространственной, временной и функциональной конфигурации (рисунок 3).

Задача построения оптимальной иерархической структуры состоит в построении множества Q иерархий с заданным функционалом

• (4)    arg min G g Q P ( G ), P : Q >  G [ °, + го ]

Множество иерархической структуры задаётся на момент времени t 0 . Динамика сложной системы знаний определяется набором функций f ,^,f с известной историей развития ситуации. Управление образует иерархическую систему знаний в момент времени t в виде отображения

• (5)    V : F х ... х F х Q ( f t ^{- 1}) >  Q ( f t ),

где Q(f) представляет собой информацию о внешней среде.

Управление иерархической системой знаний

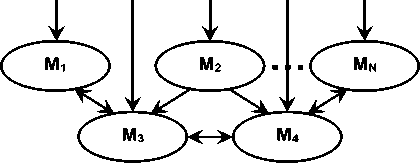
Рисунок 3 - Иерархическая среда сложной системы знаний: Mi ,..., MN - модели знаний

Управление в начальный момент времени представляется как отображение.

• (6)    у* : F ^ Q ( f t ).

Совокупность управлений v t на интервале реализации обозначается v ⁼( v ¹,—, V ^T) и рассматривается как управляющая структура иерархической системы.

На каждом иерархическом уровне вводится описание последовательности операций в пространствах состояний и ситуаций в соответствии со следующими определениями.

Определение 4. Пространство состояний X сложной системы знаний включает в себя тип и число переменных и параметров состояния Ω , функцию отображения f: Х×Ω→ R , а также описание состояний, соответствующих данному уровню иерархии.

Определение 5 . Пространство ситуации сложной системы знаний - множество элементов на данном уровне иерархии, характеризующееся параметрами ситуации и особенностями эволюционной динамики при заданном уровне внешних возмущений.

Определение 6 . Математическое описание сложной системы знаний включает множество допустимых входов U и выходов Y , множество состояний Q (пространство ситуаций), функцию перехода Л: QxU^Q и функцию выхода y Q x U ^ Y .

3 Структурный синтез онтологии сложной системы знаний

Структурный синтез и принципы организации онтологии знаний сложной системы разработаны в рамках концептуальных решений, определяющих функциональные множества иерархической среды [1]. Эти решения основаны на взаимосвязи конфигураций, характеризующих внутреннюю, отображающую и управляющую информацию. Внутренняя информация определяет целенаправленное поведение системы. Отображающая информация содержит сведения об окружающей среде и особенностях текущей ситуации. Управляющая информация - это совокупность управляющих воздействий в заданных внешних условиях.

Модель реального мира, определяющая концептуальное моделирование сложной системы знаний в режиме экстренных вычислений ( Urgent Computing - UC) [11], обеспечивает реализацию общих принципов обработки информации в рамках динамической модели СТК [2]. Интеграция сложной системы знаний с интеллектуальными технологиями и высокопроизводительными вычислениями представлена на рисунке 4.

Контроль сложной системы знаний на интервале реализации [t₀,t k ] осуществляется с использованием следующих аксиом.

Аксиома 1. Идентификация системы знаний (ситуации) осуществляется из множества альтернативных ситуаций {S j }, j =1,...,z , каждой из которых по выбранному критерию R соответствует один из альтернативных алгоритмов {A i }, i=1,_,q .

Аксиома 2. Соответствие между исследуемой ситуацией S i и оптимальной структурой алгоритма S i ^ A i , реализуется функцией интерпретации i=^), i=1, ...,q j=1,...,z , с помощью которой решается проблема использования адаптируемой структуры.

Интеллектуальные технологии

Концепция DМ

Концепция SС

Принцип МDL

ОНТОЛОГИЧЕСКИЕ ПРИНЦИПЫ ПОСТРОЕНИЯ МОДЕЛЕЙ

Высоеопроизводите-льные вычисления

Согласованность модели

Адаптивность, эволюционность

Простота и наглядность

Рисунок 4 - Парадигма и онтологические принципы интерпретации знаний в режиме UC

Аксиома 3 . Ситуация кодируется вектором S = (S 1 ,.,S u ) в u -мерном пространстве. Каждой точке S i этого пространства соответствует лучший алгоритм A i , определяемый как

• (7)    R ( A i , S i ) = min R ( A S )

j =L- q

Таким образом, сформулирована q -классовая задача интерпретации сложной системы знаний на основе конечной обучающей выборки < S j , A j > (j' = 1, ... , N), элементы которой определяются решением оптимизационной задачи

• (8)    R ( A, S_f ) ^ min ^ A. , A₁,-,A q          j

где S j (j' = 1, ... , N) - ситуации, представляющие различные части пространства { S }.

Практическая реализация аксиом 1 - 3 и концептуальных решений (1) - (8) определяет онтологический принцип использования алгоритмов контроля динамики сложной системы знаний и стратегию управления МПК в режиме UC . Решение задач адаптивного управления ведётся с помощью функции интерпретации (виртуального образа ситуации), осуществляющей генерацию стратегий управления и координацию работы МПК.

4 Онтология эволюционной динамики сложной системы знаний

Онтология пространства знаний сложной системы представлена на рисунке 5.

ОНТОЛОГИЯ ПРОСТРАНСТВА ЗНАНИЙ СЛОЖНОЙ СИСТЕМЫ

Разработка сложной системы знаний

Моделирование и визуализация решений

Аналитическая интерпретация

Геометрическая интерпретация

Генерация управленческих решений

Оценка эффективности решений

Контроль динамики сложной системы

Рисунок 5 - Онтология пространства знаний сложной системы

Модель онтологии эволюционной динамики сложной системы знаний описывается с помощью переменной yeA из допустимого множества А . Состояние системы в рассматриваемый момент времени t зависит от управляющих воздействий ue U, ye G(u). На множестве UxA задан функционал Ф(и,у) , определяющий эффективность сложной системы знаний. Задача заключается в выборе допустимого управления, которое максимизирует значение эффективности Ф(и) ^ max (u e U).

Динамика сложной системы знаний состоит в переходе из одного состояния в другое под воздействием управления U* и возмущения W*:

• (9)    U * : T ^ U , W * : T ^ W .

В функциональном отношении рассматриваемая система отличается способностью поддержания баланса равновесия между функциями и параметрами системы, управление которой реализуется набором функций:

• (10)                    F = F 1 n  n F k .

Пересечение этих множеств описывает процесс принятия решений. Каждый элемент декартова произведения функции F и информационного вектора I R

• (11)                     R С F х I r ,

определяет уровень интеллектуальности системы.

5 Онтологические принципы прогноза и управления

Онтологические принципы, определяющие стратегию прогноза и управления в сложных системах знаний, представлены на рисунке 6 функциональными блоками концептуальной онтологической модели.

КОНЦЕПТУАЛЬНАЯ МОДЕЛЬ ОНТОЛОГИИ ПРОГНОЗА И УПРАВЛЕНИЯ В ВЫСОКОПРОИЗВОДИТЕЛЬНОЙ ВЫЧИСЛИТЕЛЬНОЙ СРЕДЕ

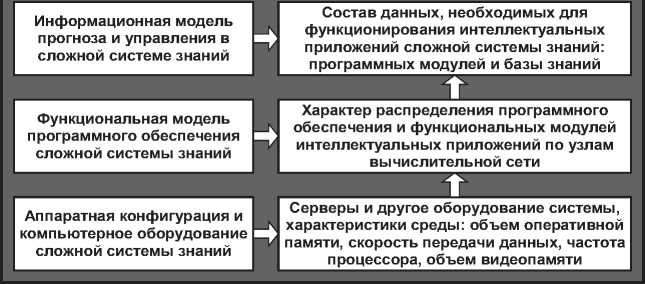
Рисунок 6 - Функциональные блоки прогноза и управления в сложной системе знаний

Концепция интеграции знаний в этом случае рассматривается как активная динамическая система (АДС) [3] управления процессом обработки информации на основе динамической модели СТК [2]. Эволюционирующая структура знаний сложной системы, реализующая стратегию UC , проходит последовательность состояний, определяемых динамической моделью СТК. Эволюционное состояние сложной системы утрачивает устойчивость при возникновении катастрофы. Эволюционные циклы на интервале реализации по своему характеру могут быть качественно различными в зависимости от уровня внешних возмущений и особенностей динамики системы. Физическое понимание качественных явлений в эволюционных процессах связано с фазовым переходом эволюционной динамики сложных систем.

Проблемы специализации, дифференциации и распределения функций в АДС знаний представлены в виде модели онтологии функционального пространства.

Утверждение 1. При формировании стратегий ИП используется механизм информирования и информационного обеспечения элементов АДС о результатах анализа альтернатив и выбора предпочтительной технологии обработки данных.

Утверждение 2 . Механизм функционирования АДС определяется целевой функцией, допустимыми множествами решений, интервалом реализации, периодами функционирования в зависимости от стратегий интерпретации и управления при движении контролируемого объекта в процессе эволюции.

Утверждение 3 . Механизм управления активной АДС формируется в виде совокупности стратегий ИП, информационного и алгоритмического обеспечении UC .

Задачи прогноза и управления сложной системой знаний в пространствах поведения и управления динамической модели СТК содержат неопределённости, свойственные задачам моделирования на основе данных динамических измерений. Процедуры принятия решений направлены на выбор вектора управляемых переменных в области поиска Z eD Z так, чтобы удовлетворить условиям выбора. Область пространства управляемых переменных, в которых выполняются все наложенные условия, называют областью работоспособности D R , а множество D=D_ZnD R - областью допустимых решений .

Критерий оптимальности представляется отображением на множестве решений

• (12)                    Q : = M i ^ R ⁺ ,

где R + – множество неотрицательных вещественных чисел.

Функция Q реализует процедуру сравнения вариантов решения m 'e M', если

• (13)                       Q ( m ') = min Q '( m ' ).

Оптимизационная задача < M, D, Q > cодержит M – пространство решений, D – ограничения в М допустимой области

• (14)                   M ' c D , Q : M' ^ R ⁺ c критерием оптимальности Q .

• 6.1    Нейродинамическое моделирование сложной системы знаний

6 Методы интерпретации знаний сложных систем

В качестве примеров практической реализации рассмотрены сложные системы знаний при обработке информации на основе нейродинамического, когнитивного и мультиагентного моделирования в пространствах поведения и управления СТК.

Процедуры синтеза нейросетевых структур [8] основаны на закономерности, определяющей подобные упорядочения в среде знаний: отношение <  для множества Х и отношение < * для множества Y . Эти операции обеспечивают условие существования взаимно однозначного отображения f (отображение подобия) множества Х на множество Y такое, что

• ⁽¹⁵⁾                         ( X 1 <  X 2 ) = f ( x 1 ) <  * f ( x 2 )■

• 6.2    Когнитивное моделирование сложной системы знаний

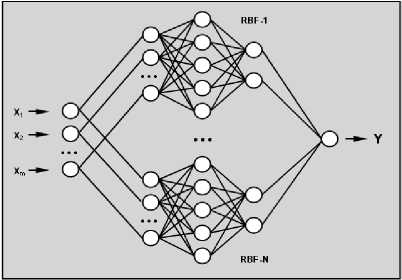
Отношение подобия для двух упорядоченных множеств является отношением эквивалентности. Отмеченная закономерность выражает фундаментальный результат преобразования информации, основанного на традиционных процедурах классической математики и нейросетевого базиса. Система нейродинамического моделирования при интерпретации сложной системы знаний представлена на рисунке 7. Здесь содержатся различные модели искусственной нейронной сети, реализующие операции преобразования знаний в пространствах поведения и управления СТК.

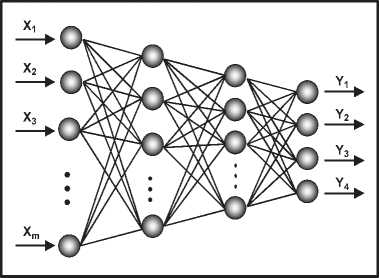
Нейросетевой ансамбль (рисунок 7 а ) реализует процедуры идентификации при оценке ситуации и логического вывода по прецеденту [9]. Многослойный персептрон (рисунок 7б) используется в задачах контроля динамических характеристик и при выявлении «скрытых» знаний в рамках концепции Data Mining [1]. Нейросетевой предиктор (рисунок 7 в ) обеспечивает прогноз эволюционной динамики на интервале реализации.

Когнитивная модель сложной системы знаний на основе когнитивной карты представляет собой параметрический векторный функциональный граф [1]. В качестве примера на ри- сунке 8 рассмотрена когнитивная карта, отображающая поведение сложной системы знаний на основе СТК.

а)

б)

Интеграция нейронечеткого и нейроэволюционного моделирования движения фрактальной структуры динамической модели катастроф

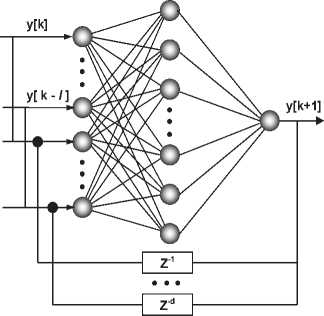
Результат моделирования при интерпретации динамики фрактальной структуры, отображающей возникновение скачкообразных явлений в физической системе

в)

Рисунок 7 - Нейронные сети в задачах идентификации (а), аппроксимации (б) и прогноза (в)

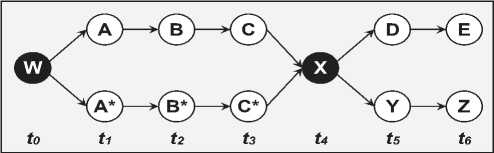
Рисунок 8 - Универсальная когнитивная карта: A – E – этапы эволюции системы;

X, D, E – фазы движения к целевому аттрактору; X, Y, Z – фазы, характеризующие потерю устойчивости

Картина поведения интерпретируется следующим образом. В результате контроля развития ситуации под воздействием внешнего возмущения W и априорных данных был реализован прогноз состояния системы на основе принципа конкуренции (альтернативы А и А* ). В течение развития ситуации применены управляющие воздействия (ситуации В и В* ), предсказанные моделью эволюционной динамики, применение которых привело к изменению поведения системы (ситуации С и С* ). Однако в момент времени t 4 (символ Х ) вследствие интенсивного внешнего возмущения произошло резкое изменение поведения системы. Это событие выходило за рамки предсказанного и вызвало изменение эволюции системы. Контроль вновь возникшей ситуации при эффективности управляющих воздействий (ситуация D ) привёл к стабилизации ситуации в области целевого аттрактора (ситуация Е ). При недостаточной эффективности контроля (ситуация Y ) возникает потеря устойчивости движения системы (ситуация Z ).

• 6.3    Мультиагентное моделирование сложной системы знаний

Практическая реализация мультиагентных систем (МАС) в сложной системе знаний рассмотрена применительно к задачам контроля транспортных систем. В качестве примеров выбраны приложения, связанные с контролем движения транспортных потоков (рисунок 9) и эвакуации пассажиров и экипажа с аварийного судна (рисунок 10) [10]. Движение агентов в процессе эвакуации реализовано с учётом угловых перемещений, локальных скоростей и ускорений нерегулярной качки. Пакетный визуализатор обеспечивает анализ ситуаций на основе МАС.

Объект управления

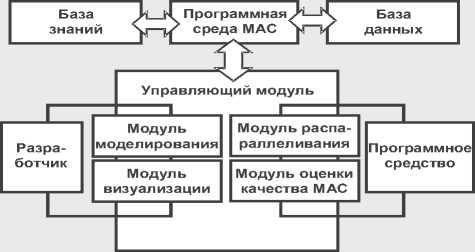
Рисунок 9 - Cреда МАС с визуализацией транспортного потока

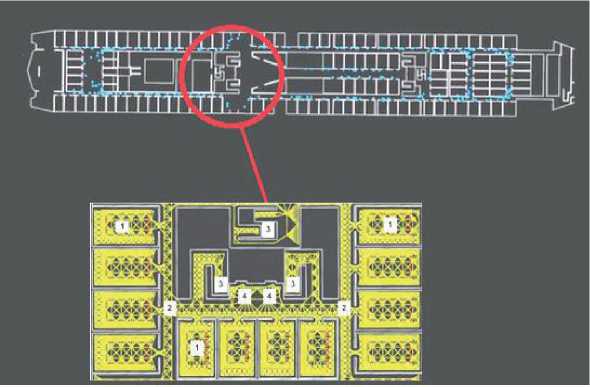
Рисунок 10 - Геометрическая модель судна (одна палуба) и фрагмент графа пешеходных перемещений (включая трапы), построенный растеризацией по квадродеревьям:

1 - каюты; 2 - коридоры; 3 - трапы; 4 - лифты

Заключение

Разработанная онтологическая система, определяющая концептуальные решения и методы интерпретации знаний, обеспечивает построение и использование моделей взаимодействия в рамках парадигмы АДС, предполагающей реализацию теоретических принципов и механизмов обработки информации в условиях восприятия случайных воздействий внешней среды на основе интеллектуальных технологий и высокопроизводительных вычислений. Онтологическая система знаний реализуется в рамках эволюционной парадигмы СТК при формировании потенциальных свойств интерпретирующих и управляющих моделей на основе искусственных нейронных сетей, когнитивной парадигмы и МАС. Ядром онтологического синтеза сложной системы знаний является МПК, обеспечивающий построение алгоритмов и программного обеспечения прикладных задач обработки знаний в различных областях практических приложений.