Онтологический синтез моделей нестационарной динамики бортовых интеллектуальных систем

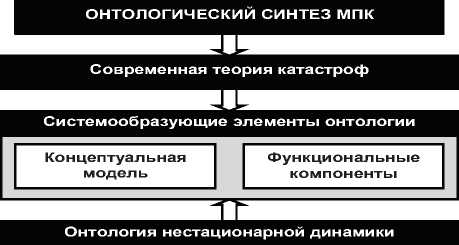
Решение задач онтологического синтеза нестационарной динамики морского динамического объекта (МДО) формализуется на основе многорежимного программного комплекса (МПК) [1]. Рассмотрение пространства нестационарной динамики как общей онтологической категории связано с выбором базовой концепции функционального пространства современной теории катастроф (СТК) [24]. На рисунке 1 показана парадигма онтологического синтеза МПК.

Пространство знаний онтологической системы при интерпретации эволюционной динамики – это совокупность всех возможных состояний МДО на интервале реализации экстренных вычислений ( Urgent Computing – UC ). Интегрированная среда онтологического

Эволюционная динамика

Синергетическое управление

Онтология интерпретации эволюции

Фрактальный анализ

Когнитивная парадигма

Рисунок 1 - Парадигма онтологического синтеза многорежимного программного комплекса

синтеза моделирования и визуализации нестационарной динамики использует следующие модели:

Ont = Ont ( M ) u Ont ( U ) u Ont ( R ) u Ont ( 5 ) u Ont ( D ), (1) где Ont(M) - метаонтология; Ont(U) - онтология управления вычислениями и моделированием; Ont(R) - онтология ограничений на роли терминов и отношений между ними; Ont(S) -онтология предметной области (ПрО); Ont(D) - онтология данных по вычислениям и моделированию.

1    Онтология нестационарной динамики

При формализации моделей онтологии ПрО Ont ( S ), составляющих общую проблемную область Ont ( P ) моделирования и визуализации нестационарной динамики, используют следующие определения [5]:

Онтология «поля знаний» ПрО нестационарной динамики

Ont ( S ) ^ Q , С) g Ont ( P )                                                          (2)

определяет множество понятий Q (объектов, процессов, явлений) и множество связей С между ними:

Q = { q k\ k = 1,..., K } , С Цс^ = 1,..., L } .                                                         (3)

Компоненты модели (1) предварительно формализуются и изучаются на базе математического и физического моделирования с учётом накопленного опыта (рисунок 2).

Аналитическая интерпретация

Геометрическая интерпретация

Эволюционная динамика системы

Движение к целевому аттрактору

Потеря устойчивости движения

Визуализация динамического образа ситуации

Когнитивная            Фракталы парадигма            Аттракторы

Рисунок 2 - Онтология, определяющая интегрированную среду многорежимного программного комплекса

Проблема математического описания нестационарной динамики МДО реализуется в рамках теории сложности с учётом структуры модели и её адекватности [6, 7].

Функция интерпретации динамических ситуаций онтологической системы реализуется с использованием множества бифуркаций В ( t ) и множества, интегрирующего среду взаимодействия W ( t ). Множество С ( t ) формируется на основе данных F ( V ( t )) параметров нестационарной внешней среды и МДО F ( D ( t )). Указанные компоненты онтологической системы определяют общую структуру процесса обработки информации в режиме UC [8] и описывают реальные ситуации эволюционной динамики в зависимости от уровня действующих возмущений.

2    Формальный аппарат онтологии нестационарной системы

Основная проблема, определяющая онтологическую систему знаний при анализе и синтезе модели взаимодействия в сложной динамической среде, связана с созданием нечёткой формальной системы (НФС), базирующейся на достижениях в области интеллектуальных технологий и высокопроизводительных вычислений.

Фундаментальными знаниями, на базе которых формулируется парадигма обработки информации, являются понятия пространства и времени. В рамках такой интерпретации при отображении эволюции нестационарной системы основное внимание обращается на наиболее важные физические аспекты, с помощью которых можно рассматривать формальный аппарат интеграции знаний.

Построение онтологической системы ведётся на основе принципа конкуренции [6]:

Ont Com ( PR )] = ( Ont ( ST ) , Ont ( NF ) , Ont ( NE )) , (4) где Ont ( ST) - онтология стандартной модели, описывающей ситуацию на основе достижений классической математики; Ont ( NF) - онтология модели, реализованной в рамках нейроне-чёткого логического базиса; Ont ( NE ) - онтология, формализующая нейроэволюционную модель.

Из числа возможных концептуальных метабазисов, соответствующих уровню метаонтологии «пространство - время», при интерпретации нестационарной системы выделяют:

Ont [ META ( t )] : Ont - A [ W , DO ], Ont - B [ W , P , t ], (5) где Ont-A [ W,DO ] - особенности отображения; Ont-B [ W,P,t ] - состояние, процесс, время t , W,DO - внешняя среда и МДО.

Концептуальный метабазис Ont-A [ W,DO ] называют естественным, так как он непосредственно связан с моделью эволюции нестационарной системы на интервале реализации. Если принимается соответствие «множество есть объект» при формализации эволюционного потенциала самоорганизующейся системы, то справедливо утверждение:

V C е Ont - A [ W , DO ] [ с ] is - a [ ob ] (6)

Это означает, что элементы объёма понятия «динамика взаимодействия» Cate С ( Ont-A [ W,DO ]) отнесены в C -категорию «объект исследования», а обобщение задачи реализации на уровне W- моделей приводит к метадиаграмме интерпретации динамики системы [9].

Таким образом, естественный метабазис Ont-A [ W,DO ] задаёт объектную метаонтологию, язык которой L ( Ont-A [ W,DO ]) обладает логической моделью в форме заданной импликации. Концептуальный базис Ont-B [ W,P,t ] называют «физическим», содержащим понятия «процесс», «состояние» и «время». Поэтому модельные структуры метабазиса Ont-B [ W,P,t ] являются динамическими, и эта онтология представляет собой нестационарную систему, ориентированную на моделирование процессов взаимодействия МДО в сложной динамической среде. Разработанные на основе такой формализации модели онтологии рассматриваются как составляющие общей проблемы онтологии ПрО нестационарной среды S ( NN ) и определяются критерием истинности C R ( True ) с учётом требований полноты Dem ( Full ) и непротиворечивости Dem ( Non-Contr ) аксиом и правил вывода.

Ont ( SNN ) = ( C R ( True ) [ Dem ( Full ), Dem ( Non - Contr ) ]) (7)

В результате проведённого анализа определена онтология интегрированной системы знаний S ={ S i | i=1,...,N }, которая представляется в виде:

Ont ( NET ) ^ ( Ont ( CONCEPT ), Ont ( CONNECT )) , (8) где Ont ( CONSEPT ) - множество понятий, обозначающих процессы в нестационарной среде (задачи интерпретации); Ont ( CONNECT ) - множество связей между понятиями.

3    Онтологическая система стратегических решений

Для удобства формализации информации онтологической системы используется представление в виде онтологии знаний ( Knowledge-Ontology ), которая представляет собой объединение групп « объект » и « физические эффекты », вариации поведения , динамика взаимодействия . В качестве инструментария описания задач, реализуемых в процессе нестационарной эволюции МДО, и порядком их распределения на базе функционального пространства поведения и управления СТК, используется матрица стратегических решений [6]:

{ A J { A } { A n }

M sd = [ A, X ] =

⁽ x 11 )* ... ⁽ x 1n )*

.⁽ x i m Г ... ⁽ x mn )*

Матрица (9) получена на основе преобразования исходных данных (функциональных элементов МДО) с помощью декартова произведения {mxn} множеств альтернатив А и признаков Х, формирующих отображение динамики нестационарного взаимодействия в текущей ситуации. Система альтернатив в матрице (9) приводится к единой шкале с помощью преоб- разования

( j = ( ^хл

Х„ . / х„ .

min j     max j

— X- . min j

с отображением x ji ^ x * g [ 0

Альтернативы А , формирующие структуру матрицы (9), отображают фундаментальный результат интеграции компонент динамической иерархической сети.

Совершенствование технологий обработки информации при интерпретации сложных систем связано с построением алгоритма структурного и параметрического синтеза модели взаимодействия. Последовательность операций этого алгоритма определяют функции выбора методов определения параметров и связей. Такой подход особенно эффективен в задачах прогноза, когда в зависимости от входного вектора измерительной информации последова- тельно выполняют операции смены предиктора.

Задача прогнозирования поведения нестационарной системы на основе разработанного алгоритма представляет собой цепочку преобразований:

{ X 1 ( T , S ) ,..., X n ( T , S )} ^ Y ( Out ), ..., Y n ( Out ) },                                                       (12)

где X i ( T,S , _ , X n ( T,S определяют функции интерпретации на каждом шаге эволюции системы, a Y 1 ( Out ), .. , Y _n ( Out ) - результаты прогноза исследуемой характеристики.

Интерпретация приведённой последовательности представлена на рисунке 3 в виде модели стратегического планирования операций.

Определение целей и ограничений

Стратегическое планирование операций при построении моделей взаимодействия

Построение иерархии моделей

Функциональное пространство

Определение функции интерпретации

Выбор наилучшей модели

Рисунок 3 - Стратегическое планирование операций нестационарной динамики

• 4    Онтологическая система моделирования нестационарной динамики

Моделирование нестационарной динамики в рамках онтологической системы в МПК осуществляется на основе следующих определений и утверждений.

Определение 1. Модель экстренных вычислений определяет конфигурацию среды, обеспечивающей функционирование систем раннего предупреждения ( Early Warning System – EWS ) на основе интеллектуальных технологий и высокопроизводительных вычислений.

Определение 2. Технология гибридного моделирования направлена на исследование и предсказание поведения нестационарных систем, взаимосвязи их элементов, а также выработки стратегий интеллектуальной поддержки в рамках концепции Global System Science ( GSS ).

Определение 3. Технология обработки больших объемов данных ( BigData ) [10] определяет поток данных ( WorkFlow ) в рамках сервисно-ориентированной архитектуры ( Service Oriented Architecture – SOA ). Контроль динамики взаимодействия отдалённых объектов в режиме UC поддерживается с помощью системы дистанционного эксперимента.

Определение 4. Преобразование информации характеризует последовательность событий текущей ситуации в условиях неопределённости на интервале реализации:

P —^ G 0 ^р > G 1 ^р > ... ^р > G n ,                                        (13)

где Р – множество, определяющее результат формирования исходной структуры данных интерпретируемой ситуации; G 0 , G 1 , …, G n – множества, реализующие фазы движения МДО в соответствии со стратегией СТК; р, p o , р 1 , ... , р _{n —} 1 - управляющие структуры НФС.

Определение 5. Формирование множеств G 0 , G 1 , …, G n на основе управляющих структур р, p o , р 1 , ... , р _{n —} 1 обеспечивается в процессе применения операторов интерпретации в пространствах поведения и управления для каждой фазы эволюционной динамики (13).

Утверждение 1. Функции связей реализуются через последовательность неустойчивостей, которые приводят к нарушению симметрии, созданию и поддержанию аттракторных множеств, сжимающих эти структуры.

Утверждение 2. Образ J(p i ) управляющей структуры р с ядром N(р +1 ) отображения р ₊₁ рассматривается как совокупность подсистем:

Po = N(р0), Pq = N(р,) = J(р,-1) q = 1,2,...(14)

Утверждение 3. Подсистема N(р , ) системы G , определяет последовательность

N (р,)—^ Gq, где а— - оператор включения, представляющий преобразование информации в виде:

• G, ^ J(р, )= N(р,.,)

• 5    Практические приложения нестационарной динамики

Модель функционирования МПК представляют с помощью переменной состояния y е A из допустимого множества функциональных элементов А . Состояние системы взаимодействия «МДО – внешняя среда» в рассматриваемый момент времени t зависит от управляющих воздействий ue U . На множестве UxA задан функционал Ф(и ), определяющий эффективность функционирования МПК. Задача управления заключается в выборе допустимого управления, которое при известной реакции системы максимизирует значение показателя эффективности:

Ф ( и ) ^ max( и е U ).                                                          (17)

Организация МПК, как развивающейся активной динамической системы, представляется в следующем виде:

ADS =( s е S , Str ( I , U ), G ( Str , Dec ), Int ( F ), P ( F , E ), C ( S ), I ( Dec ), U ( Dec ) ) , (18) где se S - элементы системы; Str(I, U) - структура системы в виде совокупности информационных и управляющих связей; G(Str,Dec) - порядок функционирования (оценка состояния, генерация стратегий и выбор решения), Int(F) - интервал функционирования; P(FE) - предпочтения функциональных элементов; C(S) - множества состояний МДО; I(Dec) - информация на момент принятия решения; U(Dec) - механизмы принятия управленческих решений.

Структура МПК представляет собой отображение f : T^X, определяемое как сеть топологического пространства (семантическая, иерархическая, динамическая), где Т - направленное множество. Сеть включена в множество В с Х , если существует t o < Т такое, что

( t 0 <  t ) ^ [ f , е B ] (19)

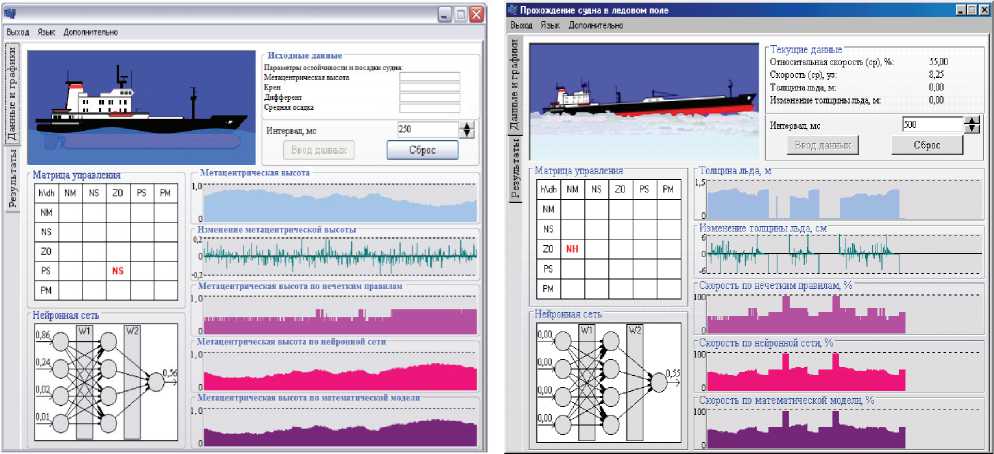
Примеры прогноза поведения МДО и корабельной посадки летательного аппарата (ЛА) в нестационарной среде приведены на рисунках 4 и 5. Стратегия моделирования на этих рисунках реализует принцип конкуренции, позволяющий определить предпочтительную вычислительную технологию в условиях неопределённости [4, 5].

а )

б)

Рисунок 4 - Пример прогноза поведения МДО в нестационарной среде: а ) движение в ветроволновом поле; б) движение в сложных ледовых образованиях

Стандартная модель на этих рисунках построена на основе классической теории управ-дения, а нейронечёткая - в виде матрицы управления и структуры искусственной нейронной сети. На рисунке 4 на дорожках справа приведены результаты моделирования определяющего параметра (метацентрической высоты на рисунке 4 а и толщины льда на рисунке 4 б ) по нечётким правилам, нейронной сети и математической модели.

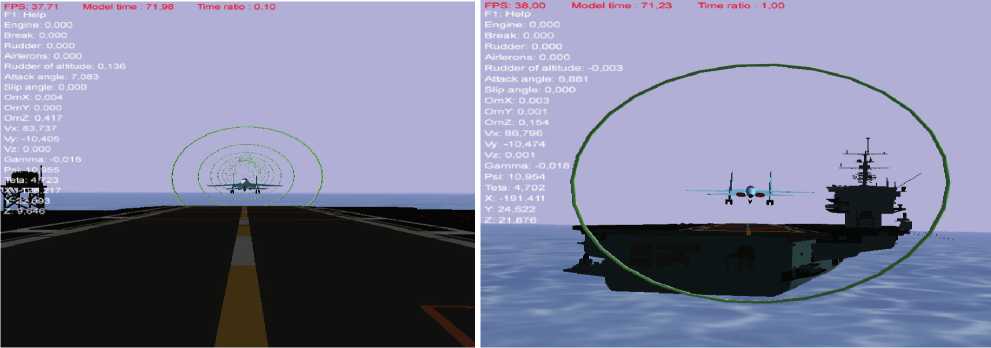
На рисунке 5 представлены результаты прогноза динамических картин на основе математического моделирования движения ЛА по глиссаде в условиях интенсивных ветроволновых возмущений. В отличие от прогноза поведения МДО, прогноз корабельной посадки ЛА при воздействии нестационарного ветроволнового возмущения выполнен при наличии пространственных ограничений (упреждение, размеры полетной палубы и её перемещения, ха- рактеристики МДО и др.). Ситуация обостряется при заходе на посадку во время ночных операций.

а )

б)

Рисунок 5 – Прогноз динамических картин, отображающих ситуации благоприятного ( а ) и критического ( б ) режима посадки ЛА на МДО

Заключение

Модель онтологической системы нестационарной динамики, определяющей функционирование МПК, позволяет описывать онтологии на разных уровнях абстракции. На основе ПрО МДО реализуется интеллектуальная технология, позволяющая сформулировать общий подход к построению НФС, реализовать стратегии управления и принятия решений с использованием онтологической системы. Формализация комплексной онтологии компонент системы интеллектуальной поддержки состоит в формальном описании интегрированной системы эволюционной динамики на основе методов концептуализации знания. В результате такой интеграции реализуется онтологическое множество объектов, знаний и связей между ними в рамках СТК.