Онтология конечно-автоматной криптографии
Автор: Шарипбай А.А., Сауханова Ж.С., Шахметова Г.Б., Сауханова М.С.
Журнал: Онтология проектирования @ontology-of-designing
Рубрика: Прикладные онтологии проектирования
Статья в выпуске: 1 (31) т.9, 2019 года.
Бесплатный доступ
На сегодняшний день совершенствование методов защиты информации является актуальной задачей. Статья посвящена применению альтернативных методов разработки более стойких и эффективных криптосистем с открытыми ключами. В качестве модели приняты конечные автоматы. Для систематизации знаний в области конечно-автоматной криптографии использована онтология. В работе рассматриваются вопросы построения онтологической модели конечно-автоматной криптографии. Предлагаемая онтологическая модель имеет четыре основных уровня: онтология представления знаний, онтология верхнего уровня, онтология предметной области и прикладные онтологии. В качестве онтологии представления знаний использована методология концептуальных карт. Онтология верхнего уровня содержит основную информацию о криптографии и теории автоматов, онтология предметной области описывает непосредственно конечно-автоматную криптографию. В качестве примера прикладной онтологии был рассмотрен алгоритм криптосистемы с открытым ключом на основе конечных автоматов. Представленная онтология построена впервые и даёт чёткое понимание применения конечных автоматов в криптографии, систематизирует полученные в ходе исследования сведения о данной предметной области, является предпосылкой дальнейшей разработки криптосистем, основанных на теории автоматов.
Онтология, концептуальная карта, конечный автомат, криптография
Короткий адрес: https://sciup.org/170178812
IDR: 170178812 | УДК: 004.822 | DOI: 10.18287/2223-9537-2019-9-1-36-49
Текст научной статьи Онтология конечно-автоматной криптографии
В условиях быстрого развития информационных технологий и внедрения их во все сферы человеческой деятельности обеспечение надёжной защиты информации, передаваемой по незащищённым каналам связи, становится актуальной проблемой современного общества. Известно, что криптография занимается исследованием методов преобразования (шифрования и дешифрования) информации с целью скрытия её содержания [1, 2], а одним из перспективных направлений в криптографии является применение теории конечных автоматов (КА) для шифрования и дешифрования информации.
Для систематизации знаний в области конечно-автоматной криптографии (КАКГ) было принято решение использовать онтологию . Известно, что онтология позволяет концептуализировать предметную область (ПрО), формализовать накопленные знания: определить ключевые понятия, задать семантические отношения между понятиями, необходимые для постановки задач и описания процессов их решения в данной ПрО. Кроме того, преимуществом использования онтологии является возможность анализа, накопления и повторного применения знаний о ПрО, полученной из разных источников [3]. Поэтому основной целью настоящей статьи является построение онтологической модели КАКГ.
В качестве инструмента был выбран общедоступный и хорошо себя зарекомендовавший на практике программный продукт CmapTools [4], который используется для построения концептуальных карт (К-карт).
-
1 Особенности создания онтологий с помощью концептуальных карт
При исследовании ПрО необходима систематизация полученных знаний. Область исследования можно представить в виде концептуальной модели ПрО, которая содержит в себе множества понятий (концептов), классификацию, свойства и характеристики этих понятий. В настоящее время применяют онтологию для наглядного представления концептуальной модели ПрО. Под онтологией понимается «формальная спецификация концептуализации, которая имеет место в некотором контексте ПрО» [5].
Формально онтологию можно определить следующим образом [6]:
О = , где:
-
■ С - конечное множество концептов (понятий, терминов) ПрО;
-
■ R - конечное множество отношений между концептами (понятиями, терминами) ПрО;
-
■ A - конечное множество аксиом или функций интерпретации, заданных на концептах и (или) отношениях.
Для построения онтологической модели КАКГ выбрана методология концептуальных карт (concept maps, К-карт). К-карта позволяет графически представить знания изучаемой ПрО. Она представляет собой ациклический граф, вершины которого есть основные понятия (концепты) рассматриваемой ПрО, а ребра – связи между понятиями (отношения) [7]. «Концепты и связи между ними имеют универсальный характер для некоторого класса понятий ПрО. Поэтому любая разработка К-карты подразумевает анализ структурных взаимодействий между отдельными понятиями ПрО» [8]. На рисунке 1 показан пример построения онтологии К-карты с помощью инструмента CmapTools.
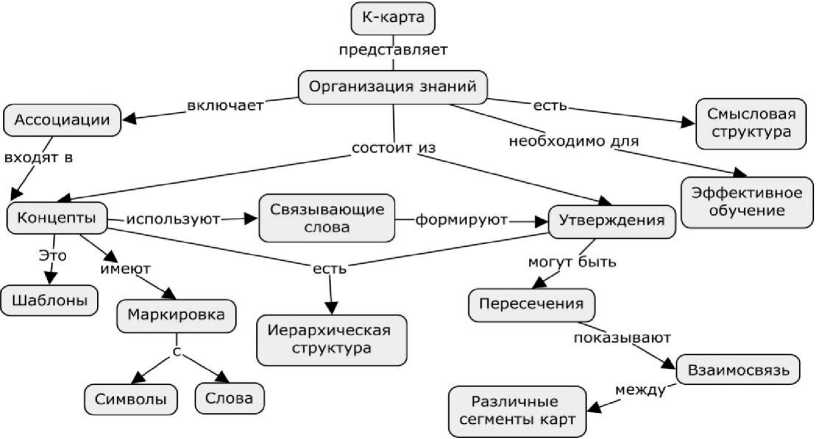
Рисунок 1 – Онтология К-карты
К-карты можно отнести к «лёгким» онтологиям, которые не содержит аксиом [9] и имеют вид:
O k = (C, R), где: С – конечное множество концептов ПрО; R – множество отношений между концептами.
Выбор К-карт для создания онтологической модели КАКГ обусловлен их следующими преимуществами [6]:
-
■ системность - К-карты позволяют представить целостный взгляд на изучаемую ПрО;
-
■ единообразие - материал воспроизводится и воспринимается эффективней, если представлен в единой форме;
-
■ научность - формирование К-карты ПрО позволяет выявить недостающие логические связи во всей их полноте;
-
■ когнитивность - в процессе построения К-карт используются все виды памяти человека, что позволяет быстро запоминать представленные картами сведения об изучаемой ПрО. Рассматриваемая ПрО представляет собой сложно-структурированную область и включает в себя понятия криптографии, теории автоматов и прикладную терминологию, содержащую понятия по конкретным реализациям криптосистем, основанных на КА. Онтологию КАКГ можно разделить на четыре основных уровня, которые показаны на рисунке 2.

Онтология представления знаний

Модель К-карты

Онтология верхнего уровня
4;
Онтологии криптографии и теории автоматов

Онтология предметной области

Онтологии конечно-автоматной криптографии

Прикладные онтологии


Прикладные онтологии в области конечно-автоматной криптографии
Рисунок 2 – Уровни онтологической модели области конечно-автоматной криптографии
Первый уровень – онтология представления знаний – описывает область представления знаний. Целью первого уровня является создание языка для спецификаций других онтологий более низкого уровня. В качестве онтологии первого уровня использована модель К-карты, показанной на рисунке 1.
Онтология верхнего уровня – это онтология криптографии и теории автоматов, поскольку ПрО объединяет криптографию и теорию КА.
Третий уровень онтологии – это онтология КАКГ, в которой даются описания основных концептов конечно-автоматной модели. По своей структуре онтология КАКГ является логическим продолжением онтологии верхнего уровня.
Четвёртый уровень онтологии – это прикладные технологии КАКГ. Данный уровень содержит специфичную информацию – концепты и отношения, которые раскрывают особенности определённых криптосистем, основанных на КА.
-
2 Онтология конечно-автоматной криптографии
КАКГ основана на использовании теории автоматов и криптографии. Каждая из этих наук включает в себя огромный понятийный аппарат. В статье выбраны основные концепты, которые дают ясное представление об изучаемой ПрО. На рисунке 3 показано объединение данных направлений. В верхней части рисунка 3 (а) концептуальной модели расположены основные концепты и отношения, относящиеся к криптографии, нижняя часть рисунка 3 (с)
содержит важные концепты и связи теории автоматов, на стыке двух онтологий (рисунок 3 (b)) представлены существующие криптосистемы, построенные на основе КА.
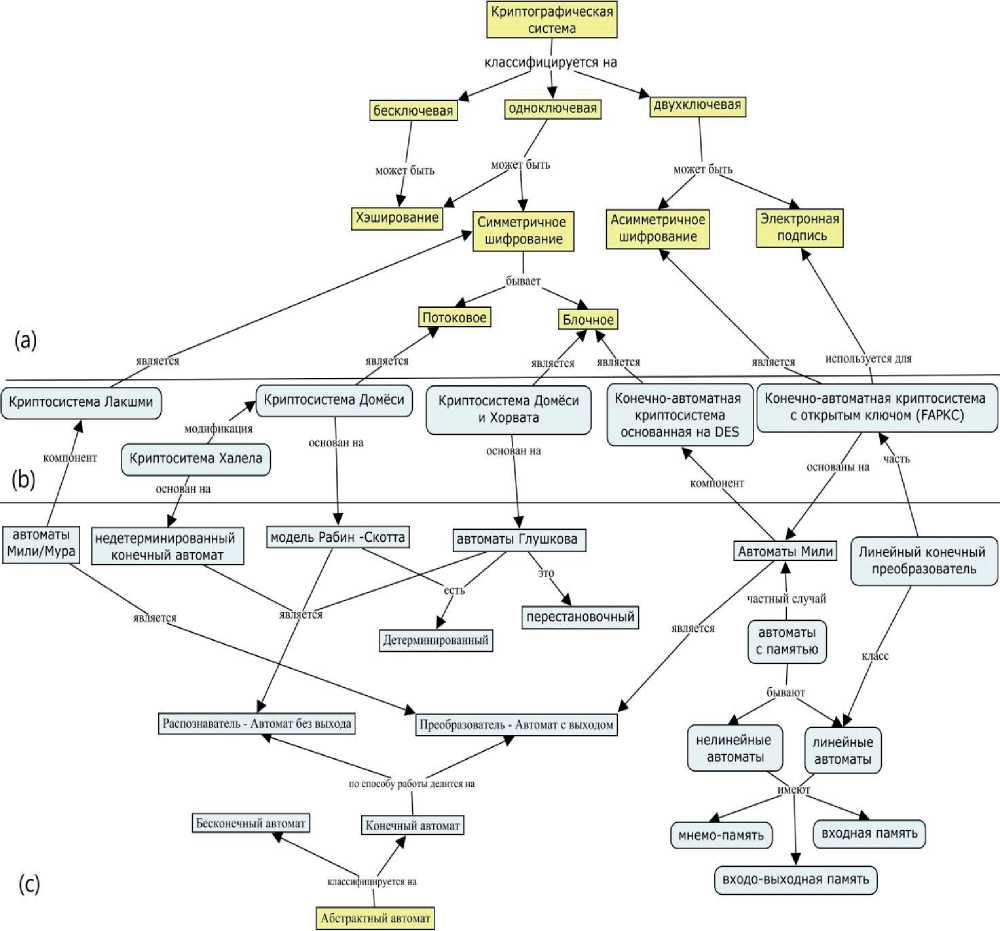
классифицируется на двухключевая | может быть бывает
| Потоковое]
Криптосистема Домеси
| модель Рабин -Скотта]
j Автоматы Мили|
| Детерминированный]
бывают бесключева^ |одноключевая может быть может быть
| Хэширование |
| Блочное| используется для
Криптосистема Лакшми
^ Криптоситема Халела
| автоматы Глушкова~| частный случай
| перестановочный |
| Распознаватель - Автомат без выхода |
| Преобразователь - Автомат с выходом]
по способу работы делится на
| Бесконечный автомат |
| Конечный автомат | классифицируется на j Абстрактный автомат | нелинейные автоматы линейные автоматы автоматы Мили/Мура
Симметричное шифрование
Асимметричное шифрование автоматы с памятью модификация
Линейный конечный преобразователь недетерминированный конечный автомат
Электронная подпись
Конечно-автоматная криптосистема основанная на DES
^входо-выходная память
Конечно-автоматная криптосистема с открытым ключом (FAPKC)
Криптосистема Домёси и Хорвата
[ мнемо-память ) ( входная памятьj
Криптографическая система
Рисунок 3 – Онтология конечно-автоматной криптографии
В онтологической модели криптографии вершиной является криптографическая система. Криптографическая система представляет собой набор из криптографического алгоритма, открытого и закрытого текстов и ключей. Криптографический алгоритм (шифр) – это математическая функция, которая используется для преобразования открытого текста в зашифрованный (шифрование) и обратно (дешифрование) [10]. Ключ является основным компонентом шифра, который непосредственно отвечает за выбор преобразований криптотекста и хранится в тайном месте. В зависимости от числа ключей криптографические системы разделяют на бесключевые, одноключевые и двухключевые.
Бесключевая криптографическая система реализует метод хэширования (hashing) или контрольное преобразование информации. Одноключевая криптосистема – это способ симметричного шифрования, в котором используется один секретный ключ, как для шифрова- ния, так и для дешифрования. Симметричная криптосистема подразделяется на блочное и потоковое шифрование. Двухключевая криптосистема применяется в асимметричном шифровании и в электронной цифровой подписи. В асимметричном шифровании используют два типа ключей: открытые - для шифрования исходного текста, и секретные - для дешифрования зашифрованного текста. Оба эти ключа связаны между собой сложным соотношением. Электронная цифровая подпись необходима для подтверждения целостности и авторства данных [11].
Криптографические системы, основанные на КА - это алгоритмы, в качестве ключей которых используются КА. В вершине онтологии теории автоматов лежит концепт «Абстрактный автомат» (АА). Согласно [12] АА - это модель дискретного устройства, которое описано пятиместным кортежем:
A =
Х - множество входных символов;
-
Y - множество выходных символов;
-
S - множество внутренних состояний;
-
5: S хX ^ S - функция переходов;
Я: SxX^ Y - функция выходов.
В случае, когда множества X, Y, S - конечны, АА является КА. Если хотя бы одно из перечисленных множеств бесконечно, то АА называется бесконечным.
По принципу однозначности функции перехода КА можно классифицировать как детерминированный или недетерминированный КА.
Детерминированность автомата заключается в выполнении условия однозначности переходов, т.е., если автомат находится в некотором состоянии и под воздействием произвольного входного символа переходит в одно и только одно состояние. При недетерминированности КА, он под воздействием одного и того же входного символа может перейти в различные состояния из множества состояний S [13].
По способу работы КА разделяют на два вида [14]:
-
■ автомат - преобразователь (автомат с выходом): данный вид автомата преобразовывает поступившую на входе информацию в выходную последовательность, т.е. реализует автоматные отображения;
-
■ автомат - распознаватель (автомат без выхода): данный вид автомата распознаёт поступившую на вход последовательность, т.е. отвечает на вопрос: принадлежит ли входная последовательность к данному множеству.
В класс преобразователей входят автоматы Мили/Мура. Согласно [15] данные автоматы имеют следующую формальную запись:
( t + 1) = 5(s (t),%(t))
Автомат Мили : , t =0,1,2,.
t у (t) = X(s(t),x(t) , ,, ,
( t + 1) = 5Ss (t),x(t))
Автомат Мура: , t =0,1,2,...
-
(t) = XW) , ,,,
КА Мили, находясь в начальном состоянии 5 (0), под действием входной последовательности x (0) x (1) ... проходит последовательность состояний 5 (0) 5 (1) ... и вырабатывает выходную последовательность у (0) у (1). . Зависимость между входными символами, состояниями автомата и выходными символами в дискретном времени t показана с помощью данных систем канонических уравнений.
В автоматах Мура, в отличие от автоматов Мили, выходная последовательность определяется только состоянием автомата в какой-то момент времени t и не зависит от входной последовательности в этот же момент времени.
Как видно из рисунка 3 автомат с памятью является частным случаем автомата Мили. Данные автоматы применяются в реализации конечно-автоматной криптосистемы с открытым ключом (FAPKC). Согласно [16], если функция дт. ¥к х XH +1 ^ ¥ для некоторых целых k, h > 0, и если КА М = < X, ¥, ¥к х X ++1 ,5, Л > может быть определён у(1) = р(у( i — 1),..., у( I — к ), х(0,..., х( i — ft)), i = 0, 1,. . ., а именно
5 (< у _ 1 , ..., у _ к, х - 1 , ., х- н >, х)) = < у0,., у _ к +1 , х0 ,., х - н+1 > ,
Л(< у _ 1, ..., у _к, х_ 1, ..., х_н >, Хо) = < уо, . , у-к+1, Хо, ..., х_+11 >, уо = р(у- 1,.,у-к, хо ,.,х-+), тогда М называется КА с памятью порядка (h, k) и обозначается через Мφ. Тогда h и k называются входной и выходной памятью автомата М соответственно. В случае, когда k=0, автомат Мφ называется КА с входной памятью порядка h.
Пусть функция /: ¥к х /р+1 х Х++1 ^ ¥, а функция у: ¥к х /р+1 х Х++1 ^ U для некоторых целых k, h > 0, p > -1, и если КА Mj= = < X, ¥, ¥к х /р+1 х Х+,5, Л > может быть определён у(0 = /(у( I — 1), ..., у( I — к ), н(1), ... , н( i — р ),х(0, ., х( i — ft)),
и (i + 1) = д(у (i — 1), .„,у(1 — к ), н(0, .,u(i — р ),х(0, .,х(1 — ft)), i = 0,1, „. а именно
5(< у -1 , .,у -к , Н о ,., и -р ,х -1 , ., х - + >,х о ) = < у о , .,у -к+1 , W 1 ,., -рр +1 , х о ,., х -++1 > ,
Л(< у-1, .,у- к,Но, .,и-р,х-1, .,х- + >,хо) = < уо, .,у- к+1, Н1, . , Н- р+1, хо, . , х-++1 >, уо = /(у- 1 ,.,у- к,Но,.,Н - р,хо,.,х-+),
Н1 = д (у- 1,.,у-к, Но,., и - р,хо,.,х-+), тогда М называется КА с псевдо - памятью порядка (h,k,p) и обозначается через Му,5.
Автомат с памятью подразделяют на линейные и нелинейные . Если функции, определяющие КА, линейны, то автомат является линейным (ЛКА). Добавление к ЛКА любой нелинейной функции приводит к нелинейному КА с памятью (НлКА).
Рассмотрим КА в качестве распознавателя.
Если для КА
A =
Если
КА Д = < X, -, 5 > с S = X называется перестановочным автоматом , если для любых a, b ∈ S ( a ≠ b ) и x, y ∈ X (x ≠ y), δ (a, x) ≠ δ (b, x) и δ (a, x) ≠ δ (a, y).
Модель Рабин-Скотта – это детерминированный КА - распознаватель.
3 Онтология ПрО
Модель включает в себя концепты из описанных в разделах 1 и 2 уровней и новые понятия, относящиеся непосредственно к КАКГ (см. рисунок 4). В КАКГ введены следующие концепты: композиция КА, обратимость КА, слабо обратимый КА с задержкой, обратный автомат. Эти характеристики стали основополагающими в разработке криптосистем на основе КА. Как показано на рисунке 3, криптосистема FAPKC основана на КА Мили, а именно на КА с памятью. Основная идея FAPKC заключается в использовании последовательной композиции слабо обратимых КА для генерации открытого ключа, тогда как секретный ключ состоит из их обратных КА. Данная семантическая связь видна на рисунке 4. Дадим определение концептов.
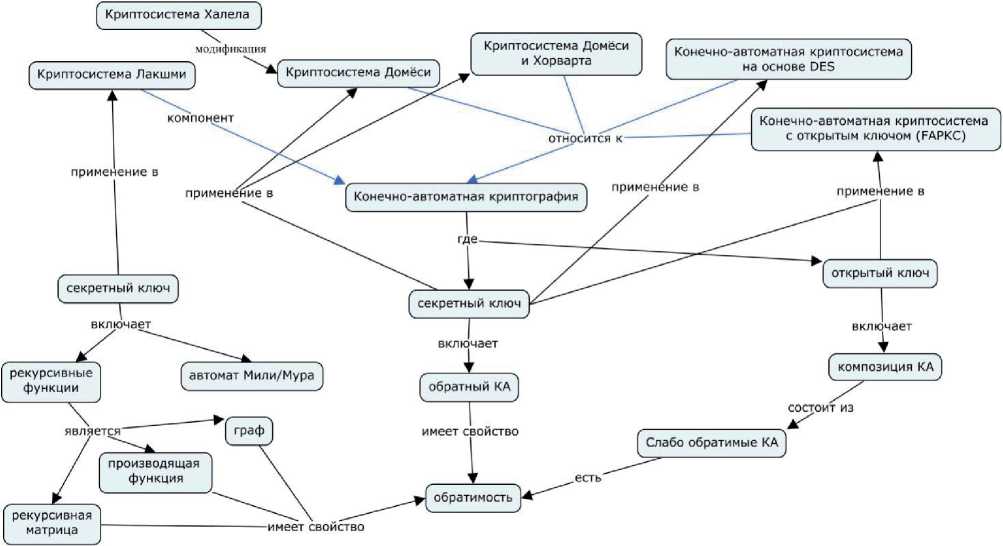
Рисунок 4 – Онтология предметной области
Пусть даны два КА
М
=<
X, Y,S, 8, Л
> и
М
'
=
Для Vs Е S и Vs ' ES ' , если Va Е Xм, 3a0 EXк: Л ' (s ' ,Л(s, a)) = a0a и |« о | = т, тогда (s‘, s ) называется парой с задержкой т ( т-парой ), т.е. s' соответствует s с задержкой т [17].
Автомат М′ называется обратным с задержкой τ к автомату М, если ∀ ∈ ∃ ∈ та кой что (s', s) является т-парой в М'^М.
Пусть заданы два КА М = =< X1,Y1 ^г,5г, Лт > и М= =< X2, Y2,S2, 52,Л2 >, где X 2 = Y 1 . Тогда композиция двух КА, определяется так:
(М^ М2) =< Xl, Y2, Si х S2, 5, Л >, где 5(< s ,,s2 >,х) = < 5((st,х),52(s2,Л1(s1,x)) >,Л(< sL,s2 >,х) = Л2(s2M1(s1 ,%)), х Е X 1,s 1 Е S1 ,s2 Е S2.
Если функция у: Y-lт х Y2р+1 ^ Y2, а функция /: X1t+1 ^ Y-l , то КА С' (М ^ , Ма) с памятью порядка (p + t,r) определяется так:
-
У(0 = g (у(i - 1), ., У(i - г),/(х(0, ., х(i - 0), ., f(x (i - р ), ., х(i - р - t)))
= g ' (у(i - 1), .,У(i - г),х(0,.,х( i -р - t)),i = 0,1,.
Конечно-автоматная криптосистема на основе DES оперирует КА с такими же характеристиками, что и в криптосистеме FAPKC.
Криптосистема Домёси (P. Dӧmӧsi) схожа с криптосистемами, построенными на основе КА Мили, тем, что для шифрования и дешифрования использует ключевой автомат. Ключевой автомат представляет собой матрицу перехода перестановочного автомата без выхода. Нужно отметить, что для дешифрования используется обратный ключевой автомат. P. Dӧmӧsi спроектировал симметричную криптосистему для поточного шифрования, основанную на Рабин-Скотта модели КА. Для блочного шифрования нашли своё применение произведения автоматов Глушкова (перестановочные автоматы без выхода) [18].
Заметим, что для обратимости автомата необходимо и достаточно, чтобы в его табличном представлении в каждой строке таблицы переходов все состояния были различны, т.е. автомат должен быть перестановочным. Это важное свойство, которое обеспечивает однозначность зашифрованного текста для любого открытого текста. Для безопасности предполагаем, что все столбцы таблицы переходов образуют перестановку набора состояний.
Как известно, дешифрование – это обратная функция к шифрованию, соответственно необходимо определить понятие обратного автомата без выхода.
Автомат Д_ 1 = < X , Q,5~ 1 >, с функцией переходов 6~ 1(6, х) = а, где а , b Е Q ,х ЕХ называется обратным к автомату Д = < X, Q,5 > тогда и только тогда, когда 5 (a, x)=b.
Тогда для Vа, b Е Q (а ^ b ) и для Vx Е X * выполняется равенство Д~ 1(Д(%)) = х [19].
Криптосистема, предложенная Лакшми (Lakshmi), использует автоматы Мили/Мура и рекурсивную функцию. КА является компонентом данной системы и входит в состав секретного ключа. Он предлагает использовать такие рекурсивные функции как рекуррентная матрица, производящая функция и граф, для которых определяется обратимость [20].
Рекуррентная матрица - это квадратная матрица порядка n, n> 0, элементы которой взяты из рекуррентного соотношения, например, это могут быть числа Фибоначчи. Данная матрица должна быть обязательно невырожденной .
Производящая функция /(%) для рекуррентного отношения есть многочлен порядка (n-1) и имеет вид: /(х) = а0 + агх + ... + ап_гхп_ 1.
Обратный многочлен FQx) к многочлену /(х) является многочленом степени (n-1), если удовлетворяет следующему свойству: / * F = 1.
Пусть граф есть структура G = ( V , Е , ф ), где V - это непустое множество, элементы которого называются вершинами или узлами, представляет собой набор из двух элементных подмножеств V, называемых ребрами, а – это функция с областью и совместной областью Р( (V).
Пусть функция /( G ) преобразует граф в число n , а функция /(и) является обратной к функции /( Gy Матрица смежности A определяет граф G. Обратное неверно. Путём перестановки вершин группы G можно получить множество матриц смежности. Следовательно, должна быть предоставлена дополнительная информация для обеспечения инъективного свойства отображения.
-
4 Прикладные онтологии
Прикладные онтологии КАКГ охватывает широкую область знаний и предназначены в первую очередь для того, чтобы описать концептуальную модель конкретной задачи или приложения. Данный уровень описывает концепты, зависящие от верхних уровней онтологии. В статье приведён иллюстративный пример прикладной онтологии асимметричного криптографического алгоритма на основе КА – FAPKC. Данный алгоритм включает в себя большую часть описанных концептов. FAPKC с момента создания подвергся модификациям, которые представлены на рисунке 5. Нужно отметить, что общий алгоритм FAPKC остался неизменным, менялись виды используемых в криптосистеме автоматов.
Концепция конечно-автоматной криптосистемы с открытыми ключами заключается в том, что для шифрования открытого текста и верификации подписи используется открытый ключ, который состоит из последовательной композиции обратимых автоматов, в то время как обратные им автоматы входят в состав закрытого ключа, который используется для расшифровки и подписи сообщения. Считается, что без знания секретного ключа трудно инвертировать последовательность композиции автоматов [16].
Общая схема работы алгоритма FAPKC представлена на рисунке 6.
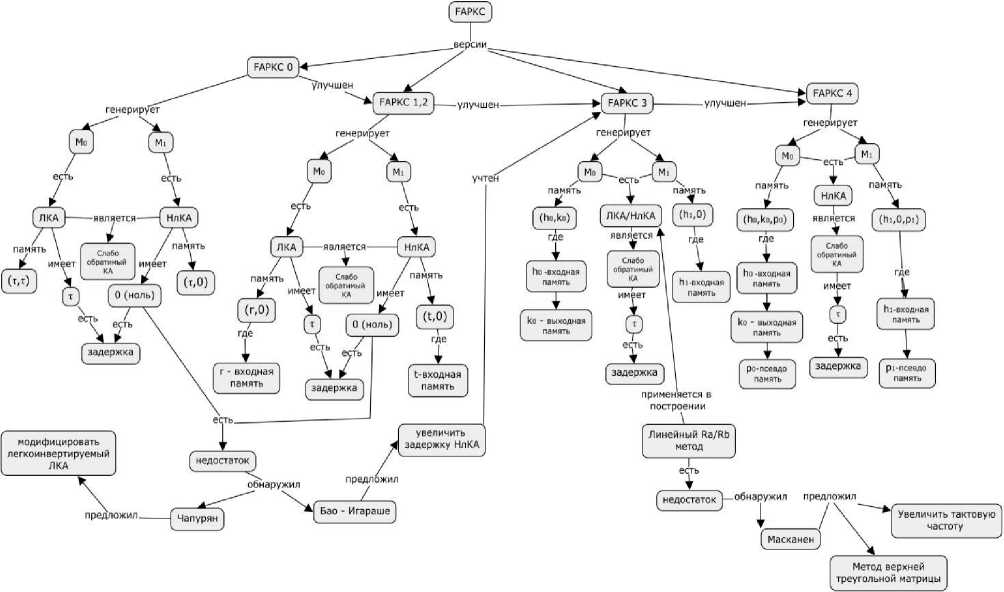
Рисунок 5 - Прикладная онтология FAPKC
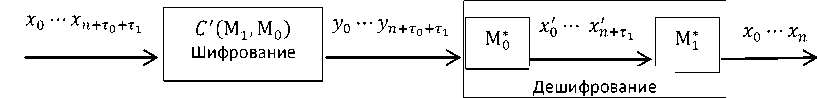
Рисунок 6 - Схема работы FAPKC
В отличие от теории чисел, где большое число можно всегда разложить на простые сомножители, для которых порядок их взаимного расположения в произведении не важен, в теории КА в композиции примитивных автоматов имеет значение как их набор, так и порядок взаимного расположения примитивных автоматов в композиции. Другими словами, композиция КА из примитивных автоматов не обладает свойством коммутативности. Поэтому разложение композиции КА на примитивные автоматы позволяет создавать сверхнадёжные системы защиты информации [21].
Общий алгоритм FAPKC.
В конечно-автоматной криптосистеме с открытыми ключами пользователь выбирает открытый и закрытый ключи по следующему алгоритму.
-
1) генерируются обратимый автомат M o =
o,5o,Xo> с памятью порядка (г0, О0 ) и обратимый к нему автомат М 0 =q,5q ,Aq> с памятью порядка (г0*, 00) и с задержкой т0. -
2) генерируется обратимый автомат M i =
1,51,X1> с входной памятью порядка - К г и обратный к нему автомат М = =^ ,5 ^ ,Л ]_ > памятью порядка (т г , h г) с задержкой т 1 . -
3) строится композиция автоматов M 1 и Mo СЧМх» 0) ) =
. -
4) определяется т. Выбирается произвольное состояние se автомата С ММг ,М0), которое и будет началом шифрования. Определяются части, необходимые для дешифрования: s f^ и s fД е, для подписи и проверки: s^1 , s™, s0 , s, s,3.
-
5) открытый ключ пользователя состоит из {С 'Мг,М 0 ), s f ut,s™,se,) 0+тг}. Закрытый ключ пользователя состоит из{М 0 , М ^ , s 0л , s г 3 , s £Д 1, s £Д1 , т0, т , }.
Шифрование: К концу заданного открытого текста ⋯ добавляются произвольные символы длины ⋯ и вычисляется шифртекст по открытому ключу, уо "’ Уп+Т0+Т1 = A(Se,Xо — хn+т0+J1 ).
Дешифрование: Открытый текст получают в два этапа. Вначале вычисляется х о — х П + Т1 = Л о (< X _ 1, е , ... , X _ 1 0 , е , у J 0 _ 1 , ..., у о , у - 1, е , ■” , у - к 0 , е >, у т0 '" у п + т0 + J 1 ) .
Затем находят хо — хп = Л 0 (< х_А , е, ™,х _ hе, х J, , ^,х О >,х^, ^,х П + Т1 ).
Подпись: К концу сообщения ⋯ добавляются произвольные символы длины уп+1 — Уп+T0+J1. Затем вычисляется подпись хо—хп+T0+J1 = М^,Л0(5о,5,хо — хп+т0+J1)), используя часть секретного ключа Мо, Ml, s0,5, s15.
Проверка: Проверка подлинности подписи сообщения ⋯ проводится исполь зованием части открытого ключа СММт, Мо), s£u 1 и з£п. Вычисляется
Л(< у _ 1 ,5 , ■" , у _t0 , х J0 + Т 1 _ 1 , ■" , х о , х _ 1 ,5 , ■" , х _, 0 _Г1 + Т0 + J 1 ,5 >, х J0 + J 1 ■" х п+J 0 +J 1 ), которое должно совпадать с сообщением ⋯ .
В таблице 1 показаны характеристики версий криптосистемы FAPKC.
Таблица 1 – Характеристики криптосистемы FAPKC
|
FAPKC версии |
Вид автомата |
( г 0 , t o ) |
( г 0 , t o ) |
Задержка |
Формальное представление |
|
FAPKC0 |
M 0 -линейный КА |
(τ,τ) |
(τ,0) |
τ |
y(i) = 2 J_1 >l j у( i - j ) + S J_о B / х ,( i — j ),i = 0,1,2,™ |
|
Нелинейная функция f |
(r+1) |
0 |
f С^ о , ™,w)|Vv 1 , ™,т’г,/( 1;'о , ™, г , ) — обратима от аргумента ио |
||
|
FAPKC1 |
M 0 -линейный КА |
(r,0) |
(τ,r) |
τ |
х ' G) = S'(у ' (i — r), ™,y(0),i = 0,1,™ |
|
М 1 -нелинейный КА |
(t,0) |
(0,t) |
0 |
у ' G) = /(у ' ( i — t),™,y(o),i = 0,1,™ |
|
|
FAPKC2 |
M 0 -линейный КА |
(r,0) |
(r,r) |
r |
х ' G) = S'(у ' (i — r),™,y(0),i = 0,1,™ |
|
М 1 -нелинейный КА |
(t,0) |
(τ,r) |
τ |
у ' G) = /(у ' ( i — t),™,y(o),i = 0,1,™ |
|
|
FAPKC1 (Bao, Igarashe) |
M 0 -линейный КА |
(r,t) |
(t+τ,r) |
τ |
y(i) = Z ,_ о A j х( i — j ) + Z )=1 B j у( i — j ), i = 0,1,2,™ |
|
М 1 -нелинейный КА |
(r,0) |
(τ,r) |
τ |
y(i) = Z J=о A j х( i — j ) + Z J _ 1 Bjy (i — j ), i = 0,1,2,™ |
|
|
FAPKC3 |
M 0 -линейный/ нелинейный КА |
(h 0 ,k 0 ) |
(к о + Т о , к о ) |
τ0 |
y(i) = I y ° 1A j у( i — j ) + Z^ o B,-x( i — j ), i = 0,1,2,™ y(i) = I y ° 1 A j у( i — j ) + ! у ° о в / х( 1 — j ) + I y °_ eBj S(x( i — j ), ™,х( i —j — e)), |
|
М 1 -нелинейный КА |
(h 1 ,0) |
(Т 1 , к о ) |
τ1 |
х ' ( i ) = Z= o Ff х( i — j ) + ij1^ 6 Fj 5(х( i — j ), ™, х(i — j — e)), i = 0,1,2, ™ где 5(х(i — j ), ™,х( i — j — e)) - нелинейная функция, а – маленькое положительное целое число. |
|
|
FAPKC3 (Mes-kanen) |
M 0 -линейный |
(h 0 ,k 0 ) |
(к о + Т о , к о ) |
τ0 |
y(i) = Z - 0 1A) у( i — J ■) + Е^ о в / х( i — j ) + i ;X+1 B 1 0 _J х(i —7•) , i=O, 12, ™ |
|
М 1 -нелинейный КА |
(h 1 ,0) |
01 к о ) |
τ1 |
х ' (i) = Z y^ F, х(i — j ) + Z y i _ e F j <;(х( i — j ), ™, х(i — j — e)), i = 0,1,2, ™ |
|
|
FAPKC4 |
M 0 -линейный/ нелинейный КА |
( к о , к о ,р о ) |
(Т о + к о , к о ,р о ) |
τ 0 |
У (D = /(у(i — 1), ™,у(—к о ),и(0, ,„,u(i — р о ),х (0 , ™,х(—к о )), u (i + 1) = у(у(i — 1),™,у(—к о ),и(0, ,„,u(i — р о ),х (0 , ™,х( i — к о )), i = 0,1, … |
|
М 1 -нелинейный КА |
(к 1 ,0,р 1 ) |
( Т 1 ,к 1 ,р 1 ) |
τ1 |
у (0 = /(и(о, ™,w( i — р 1 ),х (о , ™,х( i — к 1 )), и(i + 1) = у(и(0, ™,u(i — р 1 ),х(0, ™,х( i — к 1 )), i = 0,1, ^ |
В версии FAPKC0, приведённой в [22], открытый ключ содержит составной КА из обратимого линейного автомата с памятью порядка (τ, τ) и с задержкой τ и слабо обратимого нелинейного КА с входной памятью и с задержкой 0. Две другие схемы FAPKC1 и FAPKC2 приведены в [23], где открытый ключ для FAPKC1 содержит композицию двух КА: обратимый линейный автомат с входной памятью порядка τ и с задержкой τ, слабо обратимый нелинейный КА с входной памятью и с задержкой 0. В работе [24] доказано, что FAPKC1 небезопасен в шифровании и предлагается модификация с использованием квазилинейных КА. В [23] разработан метод генерации своего рода нелинейных слабо обратимых КА; затем две схемы, названные FAPKC3 и FAPKC4, были предложены в [25, 26]. Для версий FAPKC3 были предложены иные модификации в работе [17].
Заключение
Актуальность создания онтологии КАКГ обусловлена необходимостью в систематизации полученных знаний в криптографии. Цель предложенной онтологической модели - формирование наглядной когнитивной модели, которая отражает все основные концепты криптосистем, основанных на теории автоматов, и характер их связей. Данная модель может улучшить понимание такого рода криптосистем при планировании их реализации.
Для формирования онтологии КАКГ использована методология К-карт, которая обладает такими преимуществами как системность, единообразие, научность и когнитивность.
Структура области КАКГ рассматривается как сложно-структурированный объект, который получен путём интеграции двух самостоятельных областей - криптографии и теории автоматов. Использована четырёхуровневая онтологическая модель, включающая представление знаний – методологию К-карт, онтологии криптографии и теории автоматов, онтологию КАКГ, прикладные онтологии.
Предложенную онтологию можно использовать для решения таких задач:
-
■ обеспечение общим понятийным и терминологическим аппаратом специалистов, интересующихся данной ПрО;
-
■ создание интеллектуальных систем принятия решения в криптографической защите информации;
-
■ организация эффективного поиска информации о КАКГ.
Список литературы Онтология конечно-автоматной криптографии
- Гатченко, Н.А. Криптографическая защита информации / Н.А. Гатченко, А.С. Исаев, А.Д. Яковлев - СПб: НИУ ИТМО, 2012. -142 с.
- Сущевский, Д.Г. Современные криптосистемы и их особенности / Д.Г. Сущевский, О.В. Панченко, В.Н. Кугураков // Вестник технического университета. - 2015. - №11(18). - C.194-197.
- Мирзагитов, А.А. Методы разработки онтологии по информационной безопасности, основанные на прецедентном подходе / А.А. Мирзагитов, Д.Е. Пальчунов // Вестник Новосиб. гос. ун-та. Серия: Информационные технологии. - 2013. - №3(11). - С. 37-46.
- Cañas, A.J. CMAPTOOLS: a knowledge modeling and sharing environment / A.J. Cañas, G. Hill, R. Carff, N. Suri, J. Lott, G. Gómez, Th. C. Eskridge, M. Arroyo, R. Carvajal. - http://cmc.ihmc.us/papers/cmc2004-283.pdf.
- Gruber, T.R. A Translation Approach to portable ontology specifications/ T.R. Gruber // Knowledge acquisition. - 1993. - №5 (2). - P. 199-220.


