Онтология задач интеллектуальной деятельности

К настоящему времени выполнено немало исследований и обзорных работ, претендующих на представление классификации всех типов разных задач, решаемых экспертными системами (ЭС). Однако заметно, что подход к классификации почти у всех авторов этих работ интуитивен, нет единства ни в количестве, ни в спектре названий разных задач, ни в отнесении их к аналитическим либо синтетическим. Иногда это связано с тем, что авторы «проецируют» известные задачи на отдельные предметные области (ПрО) с их свойствами и особенностями. Более того, описываются перечисляемые задачи в разных терминах, что затрудняет понимание и сравнение их содержания. Изредка встречающиеся постановки задач обычно недостаточно формальны, представлены в содержательных терминах, часто ориентированных на отдельные ПрО. Это затрудняет проведение системного анализа для автоматизации произвольной интеллектуальной деятельности, где обычно стремятся выделить отдельные подзадачи, постановки которых известны. Поэтому целью работы является введение многоуровневой классификации известных интеллектуальных задач с их постановками в едином формализме, позволяющем уточнять задачи в зависимости от уточнений свойств ПрО, в которых они появляются.

1    Известные классификации задач интеллектуальной деятельности

Проблематика экспертных систем была актуальна в 1970-80-е годы. Множество публикаций (Уотермана, Лената, Хейеса-Рота, Кленси и др.) было посвящено обсуждению того, для решения каких задач следует разрабатывать экспертные системы. Во многих этих работах был выдвинут тезис, что возможно более полный обзор таких задач может позволить разработать методы их решения и перейти в этой области от искусства разработки эксперт- ных систем к технологии. В этот период были предложены некоторые классификации задач интеллектуальной деятельности, постановки и описания отдельных задач.

И в более позднее время продолжали публиковаться новые исследования, дающие свои версии классификации задач и их описаний. Они вносили вклад в развивающуюся инженерию знаний и предназначались для целей обучения [1, 2], а также для инженеров-программистов, нуждающихся в практическом руководстве по экспертным системам, подкреплённом теоретическим материалом [3]. Настоящий обзор систематизирует основные достижения в этой области.

• 1.1    Описания различных задач

Чаще всего задачи интеллектуальной деятельности обсуждаются при отсутствии их формальных постановок. Обычно даётся только описание задач - характерные особенности, отличающие их от других задач. При этом даже наиболее «распространённые» задачи описываются по-разному.

• 1.1.1    Распространённые задачи

Характеризуя задачи анализа и синтеза авторы делают акценты на разных особенностях получения их решения. В задачах анализа требуется [4] определить неизвестные характери-стики\свойства системы\модели объекта. Результатом задач синтеза считается построение модели объекта\системы (по заданным условиям) [5] или изменение его\её конструкции [4]. В [1] задачи синтеза отличают по построению\конструированию решений из частей (компонент или подпроблем), при этом множество решений потенциально не ограничено в отличие от задач анализа . Аналитические системы предполагают выбор решений из множества известных альтернатив [1], а синтетические системы - генерацию неизвестных решений [6].

Интерпретация (данных) это: определение «смысла данных», результаты которого должны быть согласованными и корректными [1]; формирование описания ситуаций по результатам наблюдений [7]; подготовка объяснений для наблюдаемых данных [2]; определение «сущности» рассматриваемой ситуации [6]. Под это описание подпадают два разных случая. В первом случае данные являются невербальными. Это визуальные образы, звуковые сигналы и т.п., противопоставляемые чётким символьным представлениям проблемной ситуации [8]. Во втором случае данные представляют собой символьные представления - набор признаков и их значений.

Обычно диагностика определяется как обнаружение в системе неисправностей [1] некоторого класса или отклонения параметров системы от нормативных [9], но нередко даётся и другое описание этой задачи - выявление причин, приведших к возникновению ситуации [2, 4]. При этом авторы отмечают использование при решении этой задачи знаний о типичных для системы парах сигналов «стимул/реакция» [4] или о влиянии «факторов» на внешние свойства функционирующей системы [6].

Мониторинг описывается как непрерывная интерпретация данных в реальном времени и сигнализация о выходе тех или иных параметров за допустимые пределы [1]. Кленси связывает мониторинг с обнаружением «отклонения в поведении», получаемом в ответ на поданный сигнал, но не указывает явно на реальное время для этого процесса [4]. Иногда мониторинг определяется, как не экспертная, а измерительная задача (слежение за текущей ситуацией [6]), предполагающая сочетание с другими, уже экспертными задачами, такими как: диагностика, прогнозирование, планирование и коррекция (действий пользователей) [6].

Разные авторы по-разному описывают задачу прогнозирование: предсказание хода событий в будущем (на основании модели прошлого и настоящего) [7]; предсказание последствий некоторых событий или явлений (на основании анализа имеющихся данных) [1]; предсказа- ние последствий развития текущих ситуаций (на основе математического и эвристического моделирования) [6]. Задача прогнозирования связывает описание некоторых характеристик будущего поведения объекта с описанием прошлого поведения [10]. Более того, иногда прогнозирование относят к «комбинированным» задачам, т.е. и к задачам анализа, и к задачам синтеза [1, 9].

Описания задачи проектирования у разных авторов похожи друг на друга [11]. Проектирование – это определение конфигурации объектов [6], или синтез потенциальной структурной конфигурации [12], или выбор конфигурации многокомпонентных систем [3], или построение структурной организации компонентов [4], которая удовлетворяет заданным ограничениям и критериям. Аналогично проектирование по [13] состоит в построении по спецификации такого проекта, по которому можно будет произвести объект или систему. Таково же содержание большинства определений понятия «проектирование» (от термина projec-tus), анализируемых в [14], хотя большинство англоязычных источников для задач искусственного интеллекта используют термин «design» («designing»).

Описания задачи планирования у разных авторов также похожи друг на друга: выбор последовательности действий по достижению поставленной цели [3, 6], или «нахождение планов действий» для объектов-исполнителей [1], или упорядочение возможных действий для достижения заданного суммарного эффекта [15], или поиск последовательности операторов, которая преобразует начальную ситуацию в конечную [16]. В описаниях этой задачи шаги плана рассматриваются как компоненты конфигурируемого решения [3]. План не обязательно рассматривается как последовательность действий; иногда рассматривается их частичный порядок.

• 1.1.2    Менее распространённые задачи

У Кленси управление - это «простая задача» определения того, какие входные сигналы следует подать на вход системы, чтобы получить её желаемую реакцию, опираясь на её известные характеристики [4]. Важен акцент на том, что «управлять можно тем, что есть», поэтому «управление» рассматривается как процесс принятия решений в существующей системе [14]. Многие описания задачи управления довольно абстрактны: функция, поддерживающая определённый режим деятельности сложных систем [9, 17]; обеспечение выполнения процесса. На практике поддержка определённого режима функционирования системы связана с определением управления как составной задачи: интерпретация, прогноз, планирование, моделирование, оптимизация выработанных решений, мониторинг [9] или как расширение задачи мониторинга [6]. Согласно [7] «адаптивное управление поведением сложных человеко-машинных систем» «составлено» из двух задач: прогнозировать появление возможных сбоев и планировать действия, необходимые для их предупреждения. Кроме того, «управляющая система может применяться для контроля, диагностики, прогнозирования и планирования, может следить за окружающей обстановкой, распознавать происходящие события, выдавать прогноз и составлять план действий [18].

Иногда управление сводят к принятию решений [6]. Но поддержка принятия решений выделяется и в самостоятельную задачу обеспечения необходимой информацией и рекомендациями, помогающими выбрать и/или сформировать нужную альтернативу среди множества выборов при принятии ответственных решений [1].

Задача коррекции - выработка рекомендаций по устранению неисправностей [9] или определение действий по исправлению отклонений от нормального состояния [9]. Наладочные системы предназначены для выработки рекомендаций по устранению неисправностей в контролируемой системе.

Системы оказания помощи при ремонте оборудования выполняют планирование процесса устранения неисправностей в сложных объектах [7]. Но сам ремонт – это устранение неисправностей по предписанному плану [17]. « Отладку » вместе с диагностикой иногда рассматривают как единую задачу [1, 6]. Задача « постановка диагноза и выбор определённых действий » [17] трактуется как пара задач диагностика и отладка или диагностика и лечение .

Ряд авторов описывают задачу определения принадлежности ситуации к некоторому классу , при этом называют её по-разному: задача распознавания различных ситуаций [6], классификация [19], диагностика - процесс соотнесения объекта с некоторым классом объектов [1]. Часто взаимозаменяемо используются названия классификация и диагностика , поясняя, что решение задачи классификации – главный компонент диагностики [19].

Обучение традиционно рассматривается как составная задача. При обучении диагностируют ошибки при изучении какой-либо дисциплины и подсказывают правильные решения; либо диагностируют слабости в познаниях обучаемых и находят соответствующие средства для их ликвидации, планируют акт общения с учеником в зависимости от успехов ученика с целью передачи знаний [1]. Системы обучения проводят анализ знаний студентов по определённому предмету, отыскивают пробелы в знаниях и предлагают средства для их ликвидации [7].

• 1.1.3    Редкие задачи

Иногда при обсуждении спектра решаемых задач упоминается необходимость определения того, какой информации не хватает , чтобы получить множество решений. Обычно такую задачу совмещают с той задачей, для решения которой не хватает информации [6, 10]. Задачу доопределения информации мы относим к редким задачам из-за того, что она многими упоминается, но никем не определяется и даже не описывается.

Задача извлечения информации из первичных данных [3] по своему названию близка к интерпретации . Под структурным анализом сложных объектов [3] тоже обычно понимают интерпретацию. Также можно считать редкой задачу идентификации , как в [4] названа достаточно абстрактная задача анализа , отличающаяся от других использованием в качестве анализируемой информации пар сигналов «стимул/реакция».

Концептуальное проектирование – это синтез структурной конфигурации, удовлетворяющей некоторым ключевым ограничениям [12]; анализ проекта – моделирование выбранной структурной конфигурации и определения «вытекающих» из неё внешних качеств; детальное проектирование - выбор и распределение структурных компонентов, удовлетворяющих применимым ограничениям [12].

Планирование сборки – это поиск плана реализации спроектированной системы из отдельных её компонентов [4].

Диспетчирование - распределение работ во времени, составление расписаний [6].

Из описания «систем экспертного типа» ясно, что отдельно могут быть рассмотрены задачи критики принятых решений . Постановки таких задач не приводятся, но указывается на их полезность, как минимум, в учебном процессе [20]. Такие системы поддерживают сравнительный анализ гипотез и выбор решения.

Параллельно с разными типами задач анализа и синтеза, решаемыми с использованием заранее построенных баз знаний, другие авторы определяют задачи построения баз знаний . В [10] задачи построения знаний определяются, как задачи классификации, регрессии и прогнозирования в разных областях человеческой деятельности. Результат решения таких задач - математические модели зависимости свойств объекта от его атрибутов и воздействий на него с помощью обучения по прецедентам [10]; разделение множества объектов на непересе-кающиеся классы; оценка регрессии.

• 1.2    Постановки задач

В работах обычно отсутствуют формальные постановки задач; однако имеются отдельные работы, в которых описывается, что в задаче дано, и что нужно найти [11].

Постановка задачи поиска плана действий применительно к интегральным роботам в [16] заключается в следующем. Дано: начальная ситуация (объект, состояние), конечная, или целевая ситуация (объект, состояние); множество операторов, преобразующих одну ситуацию в другую. Найти: такую последовательность операторов, которая преобразует начальную ситуацию в конечную. Примеры постановок трёх задач приводятся в [13].

Задача диагностики. Дано: ситуация ненормального функционирования; необычные проявления; стандартный набор диагностических тестов. Найти: известные категории болезней, объясняющие причины признаков, и рекомендовать методы лечения.

Задача проектирования. Дано: спецификация проектируемого объекта или системы; стандартные аналитические тесты на систему и компоненты; возможные компоненты, их свойства и взаимосвязи между ними. Найти: объект или систему, которая удовлетворяет этой спецификации.

Задача планирования. Дано: спецификация достигаемого результата; отдельные действия. Найти: план, который достигает результат, удовлетворяющий этой спецификации.

Задача диагностики [21]. Дано : медицинские знания о наблюдениях, их нормальных значениях; знания о причинно-следственных связях между заболеваниями и наблюдениями, между событиями и наблюдениями, между событиями и заболеваниями; результаты наблюдений больного (значения наблюдавшихся анатомо-физиологических особенностей, значения наблюдавшихся признаков, произошедшие события). Найти : диагноз пациента, указать причину каждого заболевания (этиологию или осложнение) и объяснить все полученные значения наблюдений.

Детерминированная задача поиска знаний для фиксированной модели зависимости между значениями признаков объектов и их классами. Дано : обучающая выборка (конечное множество объектов, каждый из которых задан значениями признаков и классом, которому он принадлежит). Найти : решающее правило, которое объекту, заданному значениями признаков, правильно сопоставляет класс, которому этот объект принадлежит [22].

Наличие таких постановок позволяет видеть различие и общие черты разных задач.

• 1.3    Классификации задач

Классификация задач имеет целью установить некоторые отношения между ними. Говоря о разных экспертных задачах, авторы чаще всего базируются на дихотомии « задача анализа и задача синтеза » [4, 15]. Эти два «класса» задач различают «по способу формирования решения» [6] (см. рисунок 1). Следующий уровень в классификациях разных авторов отличается.

В [1] задачами анализа считаются: интерпретация данных, диагностика, поддержка принятия решения , а синтеза - проектирование, планирование, управление , как показано на рисунке 2. Задачи мониторинга, предсказания и обучения отнесены автором к комбинированным задачам, причём задача предсказания отнесена к комбинированным в связи с тем, что при её решении часто нет возможности выбрать решение из множества известных альтернатив.

В [4] задачи анализа различаются «по анализируемой информации». Вводятся подклассы задач управления, предсказания и идентификации: в каждом из трёх подклассов задачи анализа требуется найти значения одного из членов тройки <входные сигналы, реакция, характеристики системы> при известных двух других. Далее предлагается ввести ещё один уро- вень, на котором подклассы задачи идентификации различаются получаемым результатом: мониторинг и диагностирование (см. рисунок 3).

К задачам синтеза все авторы относят задачи проектирования и планирования [12], которые принято рассматривать на одном уровне [12, 13]. В [1] к ним добавляется управление (рисунок 2). В [6] к синтезирующим (для динамической ПрО) отнесены не только проектирование (определение конфигурации), планирование (выбор последовательности действий) и диспетчирование (составление расписаний), но и управление , а также прогнозирование, мониторинг [6] (см. рисунок 4).

В [4] проектирование дополнено спецификацией и планированием сборки (рисунок 5). Под спецификацией понимается специфицирование нового состояния существующей системы (здесь автор проводит аналогию между задачей «специфицировать цели» и задачей «планировать», предшествующей созданию графика работ).

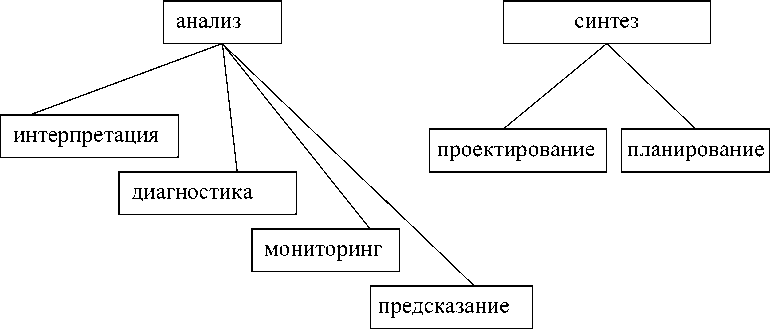
Рисунок 1 – Наиболее распространенная классификация задач

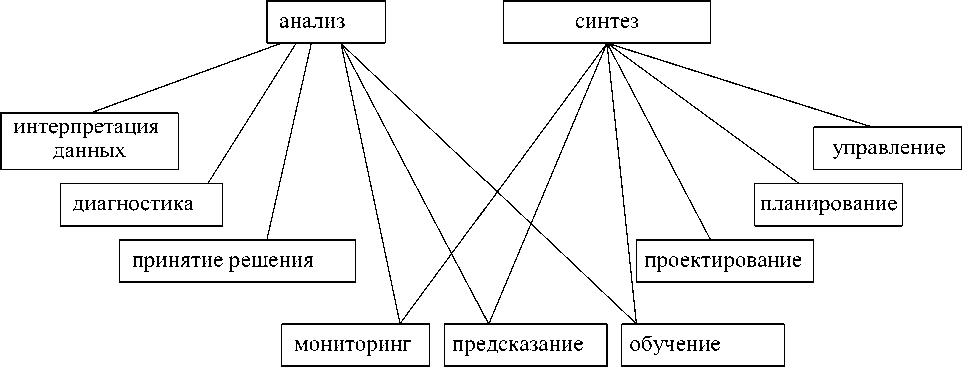
Рисунок 2 – Классификация задач в [1]

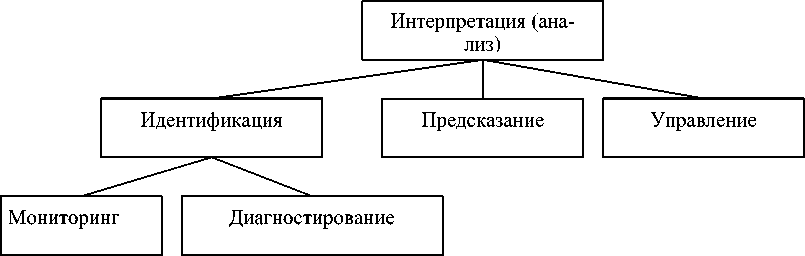
Рисунок 3 – Иерархия «родовых аналитических операций» (по Кленси) [3]

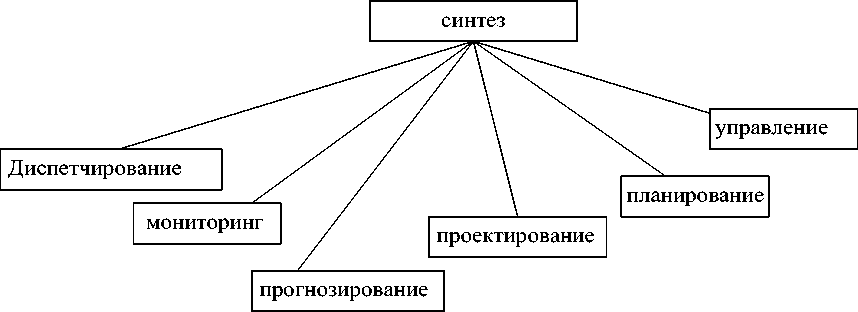
Рисунок 4 – Классификация проблемных областей синтезирующих динамических ЭС в [6]

Планирование же поставлено в [4] на следующий уровень классификации (туда же ставят планирование и другие, как отмечается в [3] со ссылкой на Reichgelt и van Harmelen), трактуя планирование как «проектирование последовательности операций». Стоящие «под» проектированием задачи конфигурирование и планирование рассматриваются либо как альтернативные задачи, либо как пара взаимосвязанных задач.

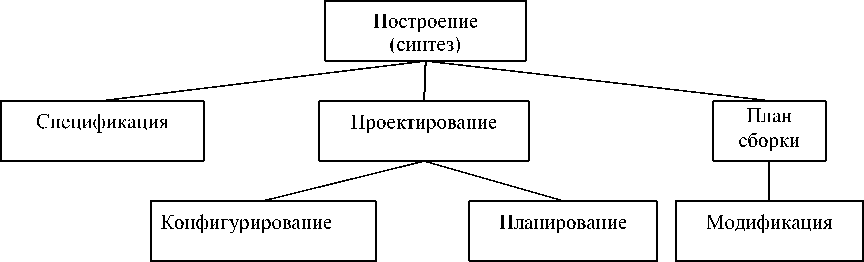
Рисунок 5 – Иерархия «родовых синтетических операций» (по Кленси) [3]

Авторы часто отмечают, что реальные задачи являются составными, определяемыми на базе простых, указанных в их классификациях. Но мнения о том, какие задачи и из каких «составляются», весьма различны. Задача выработки рекомендаций о курсе лечения в системе MYCIN включает мониторинг состояния пациента, диагностирование категории заболевания, идентификацию микроорганизмов и модификацию состояния пациента [3].

Согласно [6] коррекция – это диагностика, дополненная возможностью оценки и рекомендации действий по исправлению отклонений от нормального состояния рассматриваемых ситуаций, а управление – это мониторинг, дополненный реализацией действий. Мониторинг, дополненный другими операциями в реальных системах, рассматривается в [7] как часть диагностической системы. Задачей диагностики считается не только сопоставление диагностическому случаю известной категории болезней и поиск вероятного объяснения (причины) признаков, но и рекомендации по методам лечения [13]. Отладка , как считают, эквивалентна диагнозу плюс модификации [4].

Таким образом, до сих пор не предложено общепризнанной стройной классификации известных задач интеллектуальной деятельности.

2    Необходимость другого подхода к построению классификациии представлению задач

Приведённый обзор литературы показывает что, несмотря на то, что к настоящему времени выполнено немало исследований и обзорных работ, претендующих на представление полной классификации задач, решаемых интеллектуальными системами, почти все авторы основывают свои подходы к классификации на собственной интуиции, не пытаясь апеллировать к тем или иным фундаментальным основам. Более того, задачи описываются в разных терминах, что затрудняет сравнение их содержания. Крайне редко встречаются более или менее формальные постановки задач.

Поэтому актуальным является построение классификации задач интеллектуальной деятельности, основанной на некоторых общих принципах, единой и точно определённой с помощью математического аппарата терминологии. В настоящей работе предлагается математический аппарат, позволяющий вводить математические абстракции для всех содержательных понятий, используемых в постановках задач. В этих терминах базовая классификация задач может быть выражена достаточно абстрактно. Далее, вводятся и формально представляются различные, более частные свойства ПрО и предлагаются постановки задач на более низких уровнях абстракции или новые характерные задачи, опирающиеся на эти частные свойства. Такой подход к классификации делает её открытой для расширения.

3    Задачи индукции и дедукции

Введём математические абстракции для основных терминов, используемых в инженерии знаний, используя аппарат алгебраических систем [23].

Математической абстракцией понятия «терминология ПрО» будем считать многосортную сигнатуру Σ = {O, F, Pr}, где:

O – множество предметных символов, для каждого из которых указан сорт его возможных значений (термины, денотатами которых являются значения);

F – множество функциональных символов, для каждого из которых указаны сорта аргументов и значения функции (термины, денотатами которых являются функциональные соответствия),

Pr – множество предикатных символов, для каждого из которых указаны сорта аргументов предиката (термины, денотатами которых являются отношения).

Примечание . Функции и отношения, являющиеся интерпретациями (денотатами) функциональных и предикатных символов, могут зависеть от времени, координат пространства и других характеристик.

Математической абстракцией понятия «онтология ПрО» будем считать пару < Σ , А _Σ >, состоящую из сигнатуры Σ и множества предложений (аксиом) А _Σ на логическом языке сигнатуры Σ , представляющих те свойства терминов онтологии, которые определяются соглашениями.

Математической абстракцией понятия «база знаний, согласованная с онтологией» (БЗ), будем считать непустое множество предложений KB _Σ на логическом языке сигнатуры Σ , представляющих те свойства ПрО, которые получены путём индукции или дедукции, при условии, что множество предложений А _Σ ∪ KB _Σ непротиворечиво и никакое предложение из KB _Σ не является логическим следствием предложений из А _Σ . KB _Σ может содержать в том числе и знания эксперта ПрО.

Математической абстракцией понятия «ситуация ПрО, согласованная с онтологией», будем считать алгебраическую систему (АС) AS _Σ сигнатуры Σ , относительно которой все предложения из множества А _Σ истинны. Примером ситуации может быть и некоторая система как «множество элементов, находящихся в отношениях и связях друг с другом, которое образует определённую целостность» [24].

Будем называть задачей интеллектуальной деятельности задачу, в постановке которой в качестве входных данных и/или результатов присутствуют согласованные с онтологией < Σ , А _Σ > БЗ KB _Σ и АС AS _Σ . Рассмотрим разные классы задач интеллектуальной деятельности, называемые далее для краткости просто задачами .

В зависимости от того, требуется ли найти БЗ или она задана, можно различать задачи индукции и дедукции (рисунок 6).

В задаче индукции по обучающей выборке (заданному множеству задач с известными решениями) требуется сформировать такую БЗ, относительно которой все задачи обучающей выборки решаются правильно.

Дано : множество {AS _Σ } АС, согласованных с онтологией < Σ , А _Σ >.

Найти: KB _Σ , согласованную с онтологией < Σ , А _Σ >, такую, что относительно каждой АС из {AS _Σ } все предложения из KB _Σ истинны.

Комментарий : {AS _Σ } является математической абстракцией множества задач с известными решениями, т.е. абстракцией обучающей выборки.

Среди задач дедукции выделим задачи поиска гипотез и критики гипотезы .

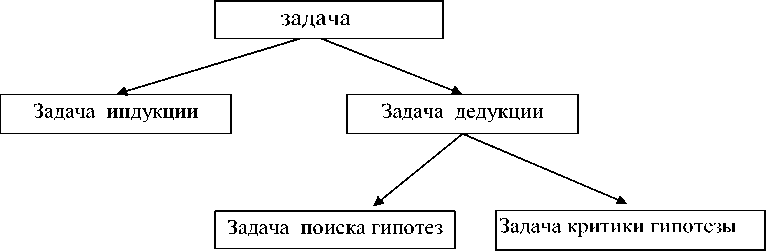
Рисунок 6 – Задачи индукции и дедукции

В задаче поиска гипотез требуется найти все гипотезы, соответствующие БЗ.

Дано : KB _Σ , согласованная с онтологией < Σ , А _Σ >.

Найти: все АС сигнатуры Σ , удовлетворяющие условию: все предложения из множества А _Σ ∪ KB _Σ являются истинными относительно каждой из этих АС.

Комментарий : искомые АС являются математической абстракцией гипотез.

В задаче критики гипотезы требуется проверить соответствие заданной гипотезы БЗ.

Дано : AS _Σ , KB _Σ , согласованные с онтологией < Σ , А _Σ >.

Найти : те предложения из множества KB _Σ , которые ложны относительно заданной AS _Σ (или показать, что таких предложений нет).

4    Задачи анализа результатов наблюдений и анализа условий на решения

Обозначим R _Σ подмножество предметных символов O 1 ⊆ O сигнатуры Σ вместе с их значениями (интерпретациями), и подмножества функциональных символов F 1 ⊆ F и предикатных символов Pr 1 ⊆ Pr, для которых заданы их частичные (возможно, не на всей области их определения) интерпретации.

Обозначим AS _Σ (R _Σ ) такую алгебраическую систему сигнатуры Σ , что предметные символы из O 1 имеют в AS _Σ (R _Σ ) такую же интерпретацию, что и в R _Σ , а интерпретация функциональных символов из F 1 и предикатных символов из Pr 1 в AS _Σ (R _Σ ) является расширением их интерпретации в R _Σ , и относительно которой все предложения из множества А _Σ их интерпретации в R _Σ , и относительно которой все предложения из множества А _Σ истинны.

Будем считать R _Σ математической абстракцией результатов наблюдения ситуации, согласованных с онтологией < Σ , А _Σ >, если существует АС AS _Σ (R _Σ ); при этом АС AS _Σ (R _Σ ) может рассматриваться в качестве математической абстракции объяснения результатов наблюдения ситуации, согласованного с онтологией.

Математической абстракцией условий на результат решения задачи, согласованных с онтологией < Σ , А _Σ > и обозначаемых далее C _Σ , является множество предложений на логическом языке сигнатуры Σ такое, что множество предложений А _Σ ∪ С _Σ непротиворечиво.

В зависимости от того, заданы ли в качестве входных данных результаты наблюдения ситуации R _Σ или условия на решение задачи C _Σ , можно различать задачи анализа результатов наблюдений и задачи анализа условий на решения (рисунок 7).

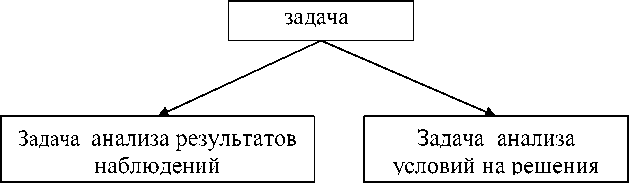
Рисунок 7 – Задачи анализа результатов наблюдений и анализа условий на решения

Задачи, рассмотренные выше, являются слишком абстрактными и, поэтому, мало реалистичными. Более полезным является подмножество декартова произведения этих двух множеств задач, которое приводит к следующим группам задач (таблица 1).

Задача поиска БЗ по обучающей выборке ситуаций, представленных результатами наблюдений рассматривается как комбинация задачи индукции и задачи анализа результатов наблюдений , в которой каждый элемент обучающей выборки представляет собой результаты наблюдения некоторой ситуации: по такой обучающей выборке требуется сформировать такую БЗ, согласованную с онтологией, что по каждому элементу обучающей выборки может быть построена модель ситуации, согласованная с онтологией и результатами наблюдений, которая соответствует БЗ.

Дано: обучающая выборка {R _Σ } (множество элементов, каждый из которых представлен результатами наблюдений некоторой ситуации, согласованными с онтологией < Σ , А _Σ >).

Найти: KB _Σ , согласованную с онтологией < Σ , А _Σ >, такую, что для каждого элемента R _Σ обучающей выборки существует АС AS _Σ (R _Σ ), относительно которой все предложения из KB _Σ истинны.

Таблица 1 – Классификация основных задач

цель задачи информация в задаче	индукция	поиск гипотез	критика гипотезы
заданы результаты наблюдений	поиск БЗ по обучающей выборке ситуаций, представленных результатами наблюдений	поиск гипотез, объясняющих результаты наблюдений	критика объяснения результатов наблюдений
заданы условия на решения	-	проектирование	критика проекта

Задача поиска гипотез, объясняющих результаты наблюдений рассматривается как комбинация задачи поиска гипотез и задачи анализа результатов наблюдений , в которой кроме БЗ заданы и результаты наблюдений ситуации: требуется найти все гипотезы, соответствующие результатам наблюдений и БЗ.

Дано : KB _Σ , согласованная с < Σ , А _Σ >, R _Σ , согласованная с < Σ , А _Σ >.

Найти: все такие АС AS _Σ (R _Σ ), что все предложения из множества А _Σ ∪ KB _Σ являются истинными относительно каждой из этих АС.

Комментарий : в этой постановке искомые AS _Σ (R _Σ ) являются математической абстракцией объяснений результатов наблюдения ситуации, согласованных с БЗ.

Задача проектирования рассматривается как комбинация задачи поиска гипотез и задачи анализа условий на решение , в которой кроме базы знаний задано непустое множество условий на результат решения задачи: требуется найти все проекты, соответствующие БЗ и условиям на решение задачи.

Дано : KB _Σ , согласованная с < Σ , А _Σ >, С _Σ (непустое), при условии: А _Σ ∪ KB _Σ ∪ С _Σ непротиворечиво.

Найти: все такие {AS _Σ }, относительно которых все предложения из А _Σ ∪ KB _Σ ∪ С _Σ являются истинными.

Комментарий : AS _Σ является математической абстракцией проекта.

Задача критики объяснения результатов наблюдений рассматривается как комбинация задачи критики гипотезы и задачи анализа результатов наблюдений , в которой кроме базы знаний даны результаты наблюдения ситуации и их объяснение: требуется установить несоответствие объяснения результатов наблюдения БЗ или подтвердить их соответствие.

Дано: KB _Σ , согласованная с < Σ , А _Σ >, R _Σ согласованное с < Σ , А _Σ >, AS _Σ (R _Σ ), согласованная с < Σ , А Σ >.

Найти: те предложения из множества KB _Σ , которые ложны относительно AS _Σ (R _Σ ), или показать, что таких предложений нет.

Комментарий : AS _Σ (R _Σ ) является математической абстракцией объяснения результатов наблюдения R _Σ .

Задача критики проекта рассматривается как комбинация задачи критики гипотезы и задачи анализа условий на решение , в которой требуется проверить соответствие проекта БЗ и условиям, которым он должен удовлетворять.

Дано : KB _Σ , согласованная с < Σ , А _Σ >, С _Σ , согласованное с < Σ , А _Σ >, AS _Σ , при условии: множество предложений А _Σ ∪ KB _Σ ∪ С _Σ непротиворечиво.

Найти: те предложения из множества KB _Σ ∪ С _Σ , которые ложны относительно заданной AS _Σ (или показать, что таких предложений нет).

Комментарий : AS _Σ является математической абстракцией критикуемого проекта.

5    Задачи, связанные с классификацией

Во многих ПрО существуют классификации ситуаций и решаются задачи, учитывающие эти классификации. В таких задачах в сигнатуру Σ входит предметный символ «класс», область возможных значений которого состоит из конечного множества значений { класс 1 ,… класс i , …, класс n }, а в БЗ KB _Σ входят предложения о свойствах ситуаций каждого класса.

Поставленные выше группы задач имеют свои уточнения; возникает также новая задача, учитывающая классификацию ситуаций (рисунок 8).

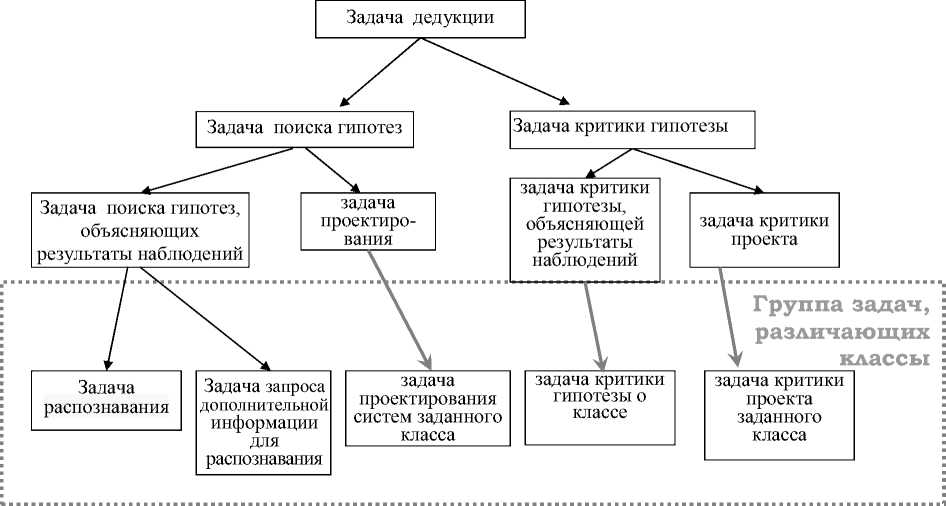
Рисунок 8 – Варианты задач дедукции, учитывающих классификации ситуаций или систем

Задача формирования знаний о классах по обучающей выборке ситуаций, представленных результатами наблюдений рассматривается как уточнение задачи поиска БЗ по обучающей выборке ситуаций, представленных результатами наблюдений , в которой элементами обучающей выборки являются не только результаты наблюдения различных ситуаций, но и класс, к которому относится каждая ситуация.

Дано : обучающая выборка {_Σ, класс = классi>}, каждый из элементов которой представлен парой, состоящей из результатов наблюдений некоторой ситуации и значением классi предметного символа «класс» для этой ситуации.

Найти: KB _Σ , такую, что для каждого элемента обучающей выборки _Σ, класс = классi> существует AS_Σ(_Σ, класс = классi>), относительно которой все предложения из KB_Σистинны.

Комментарий: {_Σ, класс = классi>} является математической абстракцией множества правильно классифицированных ситуаций, заданных результатами наблюдений; AS_Σ(_Σ, класс = классi>) является математической абстракцией объяснения классификации ситуации, заданной результатами наблюдений; KB_Σявляется математической абстракцией БЗ, содержащей описания свойств классов.

Задача распознавания рассматривается как уточнение задачи поиска гипотез , объясняющих результаты наблюдений, в которой требуется найти все гипотезы о классе ситуации, описанной результатами наблюдений.

Дано : KB _Σ , R _Σ , согласованные с < Σ , А _Σ >.

Найти: множество H R,KB, _Σ = { класс i1 , ..., класс im }, состоящее из всех таких значений предметной переменной «класс», что существуют АС AS _Σ (_Σ, класс = классi1>), ..., AS_Σ(_Σ, класс = классim>), относительно каждой из которых все предложения из множества А_Σ∪KB_Σ являются истинными.

Комментарий: АС {AS _Σ (_Σ, класс = классi>)} являются математическими абстракциями объяснения различных классификаций одних и тех же результатов наблюдений.

Будем говорить, что БЗ KB _Σ удовлетворяет условию разделимости классов, если для любой пары _Σ, класс = классi>, для которой существует такая АС AS_Σ(_Σ, класс = классi>), относительно которой все предложения из KB_Σистинны, и в KB_Σсуществуют ложные предложения относительно любой АС AS_Σ(_Σ, класс = классj>), при любом j ≠ i.

Математической абстракцией запроса дополнительной информации, обозначаемого далее Q _Σ , для результатов наблюдения R _Σ , согласованных с онтологией < Σ , А _Σ >, является: либо предметный символ o ∈ O \ O 1 ; либо терм f(c 1 , ..., c k ) , где c 1 , ..., c k – константы, а f – функциональный символ сигнатуры Σ , причём если f ∈ F 1 , то < c 1 , ..., c k > не принадлежит частичной области определения символа f , заданной в R _Σ ; либо формула p(c 1 , ..., c k ) , где c 1 , ..., c k – константы, а p – предикатный символ сигнатуры Σ , причём если p ∈ Pr 1 , то < c 1 , ..., c k > не принадлежит частичной области определения символа p , заданной в R _Σ .

Математической абстракцией ответа на запрос Q _Σ , обозначаемый далее AQ _Σ , является либо значение предметного символа o , либо значение терма f(c 1 , ..., c k ) , либо значение формулы p(c 1 , ..., c k ) , такие, что существует такая АС AS _Σ (_Σ, AQ_Σ), что ни одно из предложений А_Σне является ложным относительно AS_Σ(_Σ, AQ_Σ).

Задача запроса дополнительной информации для распознавания рассматривается по аналогии с последовательным статистическим анализом. В ней по результатам наблюдений ситуации, для которых существует более одной гипотезы о классе, требуется предложить дополнительное наблюдение ситуаций, которое гарантированно позволит сократить множество гипотез.

Дано : KB _Σ , удовлетворяющая условию разделимости классов, R _Σ , такое, что для него множество H R,KB, _Σ имеет мощность не меньше двух.

Найти: такой запрос Q _Σ дополнительной информации для результатов R _Σ , согласованных с онтологией < Σ , А _Σ >, что если R’ _Σ есть R _Σ , объединенное с AQ _Σ , то множество H R’,KB, _Σ имеет меньшую мощность, чем множество H R,KB, _Σ .

Комментарий: множество H R,KB, _Σ является математической абстракцией множества гипотез о классе ситуации, полученных на основе БЗ KB _Σ и результатов наблюдений R _Σ , а множество H R’,KB, _Σ является математической абстракцией множества гипотез о классе ситуации, полученных на основе БЗ KB _Σ и результатов наблюдений R _Σ , дополненных результатами ответа AQ _Σ на запрос Q _Σ дополнительной информации.

Задача проектирования систем заданного класса является уточнением задачи проектирования . В ней требуется по БЗ и множеству условий на результат решения найти проект системы заданного класса.

Дано: KB _Σ , значение класс m предметного символа «класс», С _Σ .

Найти: все такие {AS _Σ (< класс = класс m >)}, относительно которых все предложения из А _Σ ∪ KB _Σ ∪ С _Σ являются истинными.

Комментарий: найденные {AS _Σ (< класс = класс m >)} являются математической абстракцией множества проектов заданного класса класс m .

Задача критики гипотезы о классе рассматривается как уточнение задачи критики объяснения результатов наблюдений . В ней требуется проверить соответствие заданной гипотезы о принадлежности ситуации заданному классу БЗ.

Дано : KB _Σ и R _Σ , согласованные с < Σ , А _Σ >, значение класс i предметного символа «класс», AS _Σ (_Σ, класс = классi>).

Найти: те предложения из множества KB _Σ , которые ложны относительно AS _Σ (_Σ, класс = классi>), или показать, что таких предложений нет.

Комментарий: AS _Σ (_Σ, класс = классi>) является математической абстракцией объяснения принадлежности результатов наблюдения R_Σклассу классi.

Задача критики проекта заданного класса рассматривается как уточнение задачи критики проекта, в которой задан класс проектируемой системы.

Дано : KB _Σ , С _Σ , согласованные с < Σ , А _Σ >, значение класс i предметного символа «класс», АС AS _Σ (< класс = класс i >).

Найти: те предложения из множества KB _Σ ∪ С _Σ , которые ложны относительно заданной AS _Σ (< класс = класс i >), или показать, что таких предложений нет.

6    Задачи для систем, состоящих из компонентов

Во многих ПрО анализируются или проектируются системы, состоящие из компонентов, и решаются задачи, учитывающие эти компоненты и отношения между ними (в том числе пространственные). В таких задачах в сигнатуре Σ присутствуют символы для обозначения компонентов и отношений между ними; А _Σ описывает множества таких свойств компонентов и отношений, которые определяются соглашениями специалистов ПрО . В БЗ KB _Σ и в условиях на результат решения задачи С _Σ присутствуют предложения о свойствах таких символов, получаемые индуктивным или дедуктивным путем.

Уточнением задач проектирования для этого случая являются задачи конфигурирования (или сборки). Постановка задачи конфигурирования совпадает с постановкой задачи проектирования, при условии, что результатом решения задачи является множество всех таких {AS _Σ }, которые описывают конфигурацию системы с помощью символов, обозначающих компоненты и отношения. AS _Σ является математической абстракцией проекта конфигурации создаваемой системы (в литературе обычно называемого спецификацией).

Аналогичные уточнения имеют место и для задач поиска гипотез, объясняющих результаты наблюдений , критики объяснения результатов наблюдений и критики проекта .

7    Задачи, в которых существенную роль играет время

Некоторые задачи связаны с онтологиями, которые обязательно содержат термины, денотаты которых являются функциональными соответствиями и отношениями, зависящими от времени. В таких задачах в сигнатуру Σ входят функциональные и предикатные символы, зависящие от времени (эти символы являются математической абстракцией атрибутов динамической системы или ситуации, зависящих от времени, одним из которых часто является состояние ). В постановках задач анализа результатов наблюдений R _Σ содержит кортежи значений таких символов, и в А _Σ , KB _Σ и С _Σ присутствуют предложения, использующие такие символы.

Множества функциональных и предикатных символов сигнатуры Σ , зависящих от времени , будем обозначать F t и Pr t . Пусть {r t1 ,.. r tm } - подмножество символов из F t ∪ Pr t , для которых заданы их интерпретации в некоторые моменты времени.

Функциональный терм (атомную формулу) с таким символом (r tj ⊆ F t ∪ Pr t ), одним из аргументов которой является момент t, обозначим через r tj (…, t, …). Функциональные термы (атомные формулы) символа r tj , аргумент которых, соответствующий моментам времени, имеет значения t 0 , …, t k , обозначим через {r tj (…, t 0 , …), …, r tj (…, t k , …)}. Если функциональные термы (атомные формулы) {r t1 (…,t 0 ,…), … r t1 (…,t k ,…),.. r tm (…,t 0 ,…), … r t1 (…,t k ,…)} вместе с их значениями входят в R _Σ , то в этом случае вместо R _Σ будем использовать обозначение R _Σ (t 0 , ..., t k ). Функциональный терм (атомную формулу) символа q’ с аргументом t’, соответствующим моменту времени (в который значение терма или формулы неизвестно), обозначим через q’(…, t’, …).

Постановки задач поиска гипотез, объясняющих результаты наблюдений, критики объяснения результатов наблюдений и др. для динамической ситуации не меняются, но уточняются за счёт того, что интерпретация некоторых символов зависит от времени. В ПрО, различающих классы ситуаций, значения которых зависят от времени, такими уточняющими задачами становятся задача распознавания класса ситуации, описанной результатами динамических наблюдений, и задача запроса дополнительной информации для распознавания класса динамической ситуации (рисунок 9).

Задачи проектирования (и критики проекта ) могут ставиться для динамических систем (а не только для статических систем). Среди символов сигнатуры для проектов динамических систем должны быть функциональные и/или предикатные символы, которые зависят от времени. Эти символы используются при описании динамических свойств компонентов в БЗ KB _Σ и при задании условий С _Σ на конкретную проектируемую систему. Таким образом, в задачах проектирования динамической системы в С _Σ присутствуют формулы, отражающие динамические свойства системы. Кроме уточнённых задач для динамических систем возникают и новые задачи.

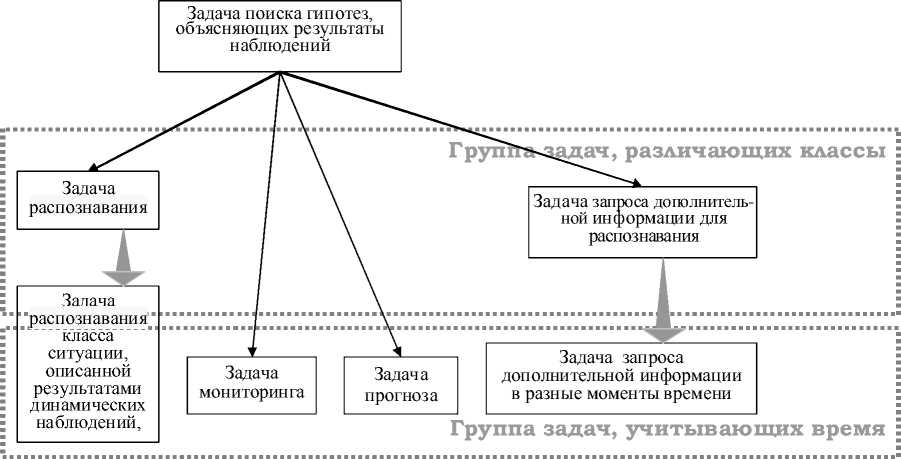
Рисунок 9 – Схема изменения спектра возможных задач в зависимости от характеристик ПрО

Задача прогноза – уточнение задачи поиска гипотез, объясняющих результаты наблюдений , в которой по значениям функциональных термов (атомных формул), зависящих от времени, заданным в некоторые моменты времени t 0 , … t k (обычно – по результатам наблюдений за динамической системой) требуется определить значения этого или другого функционального терма (атомной формулы) для заданного момента времени t’, отличного от t 0 , …, t k (чаще - для будущего момента) при заданных значениях остальных аргументов (если они есть).

Дано : KB _Σ , согласованная с < Σ , А _Σ >; упорядоченное множество моментов времени {t 0 , …, t k }; R Σ (t 0 , ..., t k ); t’ ∉ {t 0 , … t k }; q’ ∈ F t ∪ Pr t .

Найти : все такие значения функционального терма (атомной формулы) q’(…, t’,…), для каждого из котороых существует такая АС AS _Σ (_Σ(t0, ..., tk), q’(…, t’,…)>), что все предложения из KB_Σистинны относительно неё.

Комментарий : если t’ > t k , то речь идёт о прогнозе на будущее; если же t’ < t k , то речь идет о «ретроспективном» прогнозе.

Если в ПрО динамике рассматриваемых ситуаций соответствует конечное множество состояний { состояние 1 ,… состояние i , …, состояние n }, то функциональный символ «состояние», зависящий от времени, начинает «играть роль» предметного символа «класс». При этом частным случаем задачи прогноза становится задача прогноза состояния динамической системы ; в ней требуется найти значение функционального символа «состояние» в интересующий момент времени.

Наряду с задачей распознавания состояния системы , которая может быть рассмотрена для динамической системы, имеет место задача распознавания в реальном времени такого момента , когда ситуация требует принятия некоторых мер. Такое состояние системы иногда называют «критическим», отличным от нейтрального, а задачу распознавания такого состояния - задачей мониторинга . В этом случае в сигнатуру должен входить некоторый выделенный предикатный символ критическое состояние .

В задаче мониторинга требуется по результатам наблюдения динамической системы определить, является ли состояние системы критическим.

Дано : KB _Σ , согласованная с < Σ , А _Σ >; R _Σ (t 0 , ..., t k ).

Найти : такое значение атомной формулы критическое состояние (t k ), для которого существует такая АС AS _Σ (_Σ(t0, ..., tk), критическое состояние (tk)>), что все предложения из KB_Σистинны относительно неё.

Для динамической системы уточнением задачи поиска БЗ по обучающей выборке ситуаций, представленных результатами наблюдений является задача поиска БЗ по обучающей выборке ситуаций, представленных результатами наблюдений динамической системы, постановка которой получается заменой {R _Σ } на {R _Σ (t 0 , ..., t k )).

8    Задачи, связанные с планированием действий

Во многих ПрО решаются задачи, рассматривающие действия (упорядоченные хотя бы частично), приводящие к некоторой заданной цели. В таких задачах в сигнатуру Σ входят символы для обозначения действий (из конечного множества названий действий в рамках ПрО).

Обозначим D множество действий , которые можно выполнять над системой. Выполнение действия изменяет текущее состояние системы, вызывая тем самым переход её в новое состояние . Обозначим S – множество возможных состояний системы, над которой выполняются действия из D. Действие d ∈ D есть функция, отображающая S в S. Каждое действие характеризуется предусловием (условием на состояние, в котором его можно применять) и постусловием (условием на состояние, возникающее после выполнения действия). Обозначим ϕ ^jpred (s) - предусловие для действия d ^j , а ϕ ^jpost (s) - постусловие, соответственно, (аргумент s обозначает состояние, в котором вычисляется значение соответствующей формулы). В БЗ каждое действие d ^j представлено парой < ϕ ^jpred , ϕ ^jpost >.

План связывает действия с состояниями , начиная от начального и завершая целевым (конечным) состоянием. При планировании «с классическими допущениями», когда мир полностью наблюдаем и статичен, а действия детерминированы, дискретны и недопустимо их параллельное исполнение, (линейный) план представляет собой последовательность действий, которая позволяет достичь цели из начального состояния [15].

Будем называть линейным планом кортеж 0, d1, d2, ..., dn-1, dn>, для которого существует такой кортеж состояний 0, s1, s2, ..., sn-1, sn> и АС AS_Σ(0, s1, s2, ..., sn-1, sn>), относительно которой справедливы предложения:

ϕ p_red (s 0 ), ϕ p_ost (s 1 ), ϕ p_red (s 1 ), ϕ p_ost (s 2 ), ..., ϕ p_red (s _n-1 ), ϕ p_ost (s _n ).

Кортеж 0, d1, d2, ..., dn-1, dn> является математической абстракцией последовательности действий, ведущих к переходу через множество состояний, начиная от начального и завершая целевым (конечным) состоянием.

В задаче линейного планирования требуется определить множество линейных планов , выполнение которых приводит к достижению целевого состояния , удовлетворяющего заданному условию , начиная от заданного начального состояния . Задача планирования - расширение задачи проектирования , точнее - проектирования систем заданного класса (класса «последовательность действий») (рисунок 10).

Дано : D ⊆ F; {< ϕ ^jpred (s) ⇒ ϕ ^jpost (d j (s))> | d j ∈ D} ⊆ KB _Σ , s 0 ∈ S; ϕ fin (s) ⊆ С _Σ .

Найти: линейный план 0, d1, d2, ..., dn-1, dn>, для которого существует АС AS_Σ(0, s1, s2, ..., sn-1, sn>), относительно которой справедливы все предложения из KB_Σ, предложение ϕfin(sn), а также все другие предложения из С_Σ.

Постановка задачи планирования усложняется в случае невыполнения «классических допущений». Будем называть планом с параллельным выполнением действий ориентирован- ный граф G, метками вершин которого являются состояния из множества S, а метками дуг – действия из множества D. Граф содержит одну начальную вершину, в которую не входит ни одной дуги, одну конечную вершину, из которой не выходит ни одной дуги. Любая вершина этого графа лежит на некотором пути из начальной вершины в конечную. Для графа существует АС ASΣ(), относительно которой: если в этом графе из вершины с меткой s выходят дуги с метками d1, ..., dn, то справедливы предложения ϕ1pred(s), ϕ2pred(s), ..., ϕnpred(s); если в этом графе из вершины с меткой s1 выходит дуга с меткой d, входящая в вершину с меткой s2, то справедливы предложения ϕdpred(s1) и ϕdpost(s2); а если в этом графе в вершину с меткой s входят дуги с метками d1, ..., dn, то справедливы предложения ϕ1post(s), ϕ2post(s), ..., ϕnpost(s).

Задачи планирования с параллельным выполнением действий .

Дано : D ⊆ F; {< ϕ ^jpred (s) ⇒ ϕ ^jpost (d j (s))> | d j ∈ D} ⊆ KB _Σ ; s 0 ∈ S; ϕ fin (s) ⊆ С _Σ .

Найти : план с параллельным выполнением действий G, у которого начальная вершина имеет метку s 0 и для которого существует АС AS _Σ (), относительно которой справедливы все предложения из KB _Σ , и если конечная вершина имеет метку s n , то справедливо предложение ϕ fin (s n ), а также все другие предложения из С _Σ .

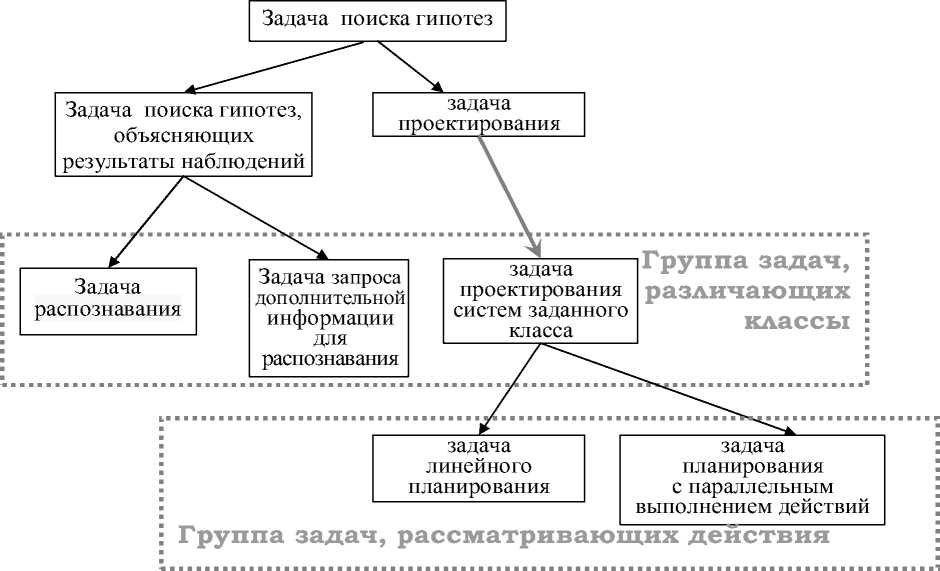
Рисунок 10 - Схема возможных задач поиска гипотез, включающая задачи планирования

В ПрО, рассматривающих планирование, также уточняется и задача критики плана .

9    Группа задач, связанных с причинно-следственными отношениями

В ряде ПрО решаются задачи относительно систем, в которых во времени протекают процессы, связанные между собой посредством причинно-следственных отношений.

Процессы, протекающие в такой системе, условно можно разделить на внешние (наблюдаемые) и внутренние (которые не могут наблюдаться непосредственно и о которых можно судить лишь по их связям с наблюдаемыми процессами). Наблюдаемые процессы обычно называют признаками, признаки имеют значения, которые получаются в результате наблюдения этих признаков и изменяются с течением времени. Помимо признаков наблюдаемыми могут быть постоянные во времени характеристики системы и происходящие в различные моменты времени события, внешние по отношению к системе, но воздействующие на протекающие в ней процессы (как внешние, так и внутренние) [25].

Причинно-следственные отношения между множеством причин и множеством следствий включают:

• ■    отношения между внутренними и внешними процессами (причинами являются внутренние процессы, а следствиями - признаки);

• ■    отношения между внутренними процессами (причинами являются внутренние процессы, а следствиями – другие внутренние процессы);

• ■    отношения между событиями и внешними процессами (причинами являются события, а следствиями – признаки);

• ■    отношения между событиями и внутренними процессами (причинами являются события, а следствиями – внутренние процессы);

• ■    смешанные отношения (причинами являются внутренние процессы и события, а следствиями – признаки) [25].

Сигнатура Σ содержит:

• ■    для каждого внутреннего процесса - функциональный символ, зависящий от времени, значение которого есть состояние процесса (обозначим множество всех таких функциональных символов F in );

• ■    для каждого внешнего процесса - функциональный символ, зависящий от времени, значение которого есть значение признака (обозначим множество всех таких функциональных символов F ex );

• ■    для каждой характеристики системы - предметный символ, значение которого есть значение характеристики системы;

• ■    для каждого события - функциональный символ, зависящий от времени (с дискретной областью определения), значение которого есть характеристики произошедшего в соответствующий момент события (обозначим множество всех таких функциональных символов F ev );

• ■    для каждого причинно-следственного отношения - предикатный символ, зависящий от времени, остальными аргументами которого являются причины, воздействующие факторы и следствия , представленные обозначающими их символами сигнатуры (обозначим множество всех таких предикатных символов P c ).

В БЗ KB _Σ каждому причинно-следственному отношению соответствует предложение вида ∀ t p c (..., t) ⇒ ϕ (..., t), где p c ∈ P c , а ϕ (..., t) - формула (причинная закономерность), устанавливающая соответствие между значениями причин, характеристик системы и значениями следствий этого отношения (аргументов отношения p c ) на некотором интервале времени от начала действия причин и до окончания их действия.

Часть внутренних процессов, протекающих в системе, является присущей системе и протекает в ней постоянно (эти процессы определены на всем временном интервале существования системы). Некоторые внешние процессы (параметры) являются присущими системе и протекают в ней постоянно; другие внешние процессы (симптомы) не являются присущими системе и могут протекать в ней только на некоторых интервалах времени. Система функционирует нормально до тех пор, пока в ней протекают только присущие ей внутренние процессы, а происходящие события не приводят к возникновению в ней новых внутренних про- цессов, не присущих ей. Каждый процесс, не являющийся присущим системе, имеет начало (момент времени, когда он возникает) и конец (момент времени, когда он исчезает).

Пусть AS _Σ - алгебраическая система сигнатуры Σ , являющаяся моделью некоторой конкретной системы (ситуации). Символы сигнатуры Σ имеют в ней следующие интерпретации:

• ■    функциональный символ f ex е F ex , обозначающий признак, - функцию, областью определения которой является для параметров вся временная ось, для симптомов – некоторый интервал времени, а областью значений – возможные значения признака;

• ■    функциональный символ f ev е F ev , обозначающий событие, - функцию, областью определения которой является некоторое дискретное множество моментов времени, а областью значений – возможные значения события;

• ■    функциональный символ f in е F in , обозначающий внутренний процесс, - функцию, областью определения которой является для процессов, присущих системе, вся временная ось, для процессов, не присущих системе, - некоторый интервал времени, а областью значений – возможные состояния процесса;

• ■    предметный символ о е O, обозначающий характеристику системы, - одно из значений этой характеристики;

• ■    предикатный символ p c е P c - множество (возможно пустое) таких кортежей отношения (причинных связей), элементами которых являются аргументы этого отношения, для которых причинная закономерность этого отношения является истинной относительно AS _Σ . Назовём причинно-следственной моделью AS _Σ системы такую алгебраическую систему сигнатуры Σ , что выполнены следующие условия:

• ■    для каждого признака существует причинная связь, в которой этот признак является следствием;

• ■    для каждого события существует причинная связь, в которой это событие является причиной;

• ■    для каждого внутреннего процесса, не присущего системе, существует причинная связь, в которой этот процесс является следствием, и существует причинная связь, в которой этот процесс является причиной;

• ■    для каждого внутреннего процесса, присущего системе, существует причинная связь, в которой этот процесс является причиной;

• ■    все предложения из БЗ являются истинными относительно AS _Z .

Обозначим R _Σ математическую абстракцию результатов наблюдения признаков, характеристик системы и произошедших событий.

Следующие задачи учитывают процессы, связанные между собой посредством причинно-следственных отношений (рисунок 11).

В задаче диагностики требуется по результатам наблюдения признаков, характеристик системы и произошедших событий определить возможные причинно-следственные модели системы. При этом диагнозом называется совокупность внутренних процессов этой модели, не являющихся присущими системе.

Дано : R _Σ (результаты наблюдения признаков, характеристик системы и произошедших событий); БЗ KB _Σ .

Найти: все возможные причинно-следственные модели ASΣ(RΣ) системы, согласованные с результатами наблюдений RΣ, относительно которых все предложения из БЗ KBΣ истинны (математические абстракции объяснения возможных диагнозов). При этом диагнозом ∆ в каждой такой модели является множество функциональных символов из Fin (∆ ⊆ Fin), обо- значающих внутренние процессы, не присущие системе, интерпретация каждого из которых в ASΣ(RΣ) имеет непустую область определения.

Обозначим R O – значения предметных символов из O (результат наблюдения характеристик системы), R ev – интерпретации функциональных символов из F ev (планируемые события); AS _Σ (R O , ∆ , R ev ) – алгебраическая система сигнатуры Σ , в которой интерпретация предметных символов из O есть R O , интерпретации функциональных символов из ∆ имеют непустые области определения, а интерпретации функциональных символов из F ev есть R ev .

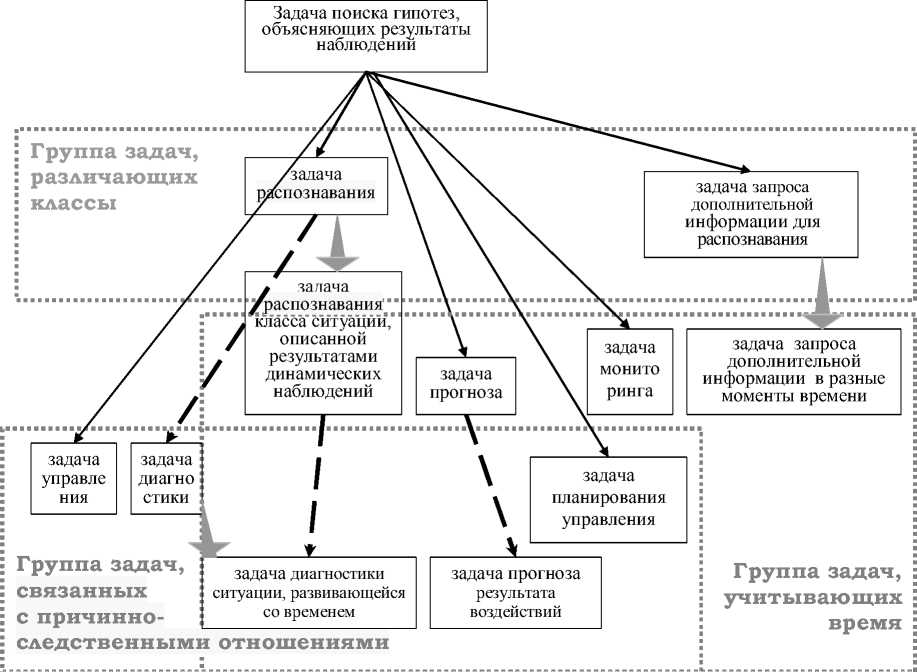
Рисунок 11 - Схема спектра возможных задач, учитывающих время

В задаче прогноза результата воздействий требуется, зная характеристики системы, диагноз и планируемые события, определить значения признаков в некоторые моменты времени в таких причинно-следственных моделях системы, которые соответствуют БЗ.

Дано : R O (результат наблюдения характеристик системы); ∆ (диагноз); R ev (планируемые события); T (конечное множество моментов времени); БЗ KB _Σ .

Найти: в каждой причинно-следственной модели AS _Σ (R O , ∆ , R ev ), относительно которой все предложения из БЗ KB _Σ истинны, значения всех функций, являющихся интерпретациями функциональных символов из F ex , во все моменты времени из множества T.

Обозначим cond (f ex , t) формулу, являющуюся условием на значение признака f ex ∈ F ex в момент времени t, а множество таких формул – Cond ⊆ C _Σ .

В задаче планирования управления требуется, зная характеристики системы, диагноз и условия на значения признаков, определить такую совокупность событий и соответствую- щие им моменты времени, при которых признаки как функции времени в причинноследственных моделях системы, соответствующих БЗ, будут удовлетворять этим условиям.

Дано : R O (результат наблюдения характеристик системы); ∆ (диагноз); Cond (условия на значения признаков), БЗ KB _Σ .

Найти : R ev (совокупность событий и моментов времени), при которых признаки как функции времени в причинно-следственных моделях системы, соответствующих БЗ, будут удовлетворять этим условиям.

Задача критики гипотезы о диагнозе может рассматриваться как уточнение задачи критики гипотезы о классе (поскольку множество возможных диагнозов может рассматриваться как своего рода класс).

10 Составные задачи

В литературе часто отмечают, что ЭС реализуют составные задачи, т.е. решают взаимосвязанную комбинацию задач. Повседневная интеллектуальная деятельность часто бывает связана с принятием разных типов решений: сбор информации, диагностика, ремонт, прогноз, и т.п., часть из которых является интеллектуальными задачами ¹ . Примерами неинтеллектуальных задач в медицине можно считать сбор первичной информации о больном; назначение общего плана лечения больному, после того, как его диагноз установлен; мониторинг значений признаков на соответствие их прогнозу (рисунок 12). Многие известные ЭС предназначены для поддержки решения одной интеллектуальной задачи и нескольких неинтеллектуальных, использующих общую информацию.

Современная парадигма автоматизации интеллектуальной деятельности (автоматизации с целью повышения качества принятия ответственных решений специалистов) требует не только дать возможность использовать при решении интеллектуальных задач самые современные и проверенные знания, но и позволить группе экспертов (лицам, ответственным за уровень знаний) создавать стандарты знаний и управлять их качеством [26]. При такой автоматизации единая интеллектуальная программно-информационная система должна «комбинировать» поддержку решения всех задач анализа результатов наблюдений (и других задач принятия решений на основе знаний) и задач индукции для формирования и коррекции используемых БЗ.

Составной задачей интеллектуальной деятельности будем считать совокупность не менее двух совместно решаемых интеллектуальных задач (и, возможно, нескольких неинтеллектуальных задач), связанных общей информацией.

Примером составной задачи является задача синтеза реализуемого проекта . Реализуемость проекта системы означает, что может быть построен план создания системы по этому проекту. Действия и состояния в этом плане связаны с элементами, из которых создается проект. Для реализуемого проекта одновременно ставятся и задача синтеза проекта , и задача синтеза плана построения системы по синтезированному проекту, т.о. задача синтеза реализуемого проекта является составной. Частным случаем составной задачи синтеза реализуемого проекта является задача синтеза реализуемой конфигурации (вместе с задачей синтеза плана сборки системы по проекту конфигурации).

Другой пример составной задачи – регулярный мониторинг состояния, когда требуется определять, является ли состояние системы отличным от нейтрального, регулярно в заданные моменты времени или с заданным интервалом (пример – наблюдение за больными в па- латах интенсивной терапии, регулярные медосмотры или диспансеризация работников предприятий).

Предварительный диагноз; значения признаков

диагностика

(уточнение диагноза)

обследование

(дообследование)

Диагноз; значения признаков

Знание о клини- Знание о ческой картине воздействиях I I         ■ 1

заболеваний I-----i лечения !

планирование лечения (коррекция плана)

Диагноз; значения признаков

иагноз;

прогнозирование (уточнение прогноза)

монито ринг начения признаков

Диагноз; значения признаков; лечебные воздействия

ожидаемые значения

Рисунок 12 - Пример совокупности задач, связанных общей информацией

Наконец, еще одним примером составной задачи является задача технической диагностики автономного робота, решаемая в процессе выполнения им миссии (задания). Автономный робот – это система, состоящая из нескольких подсистем: двигательной подсистемы, подсистемы энергопитания, различных сенсорных систем, часто дублирующих друг друга для повышения надежности. В процессе выполнения миссии подсистемы или их отдельные узлы могут выходить из строя. При этом робот в пределах возможного должен продолжать выполнение миссии, возможно, в усеченном виде. Задача технической диагностики состоит в постоянном мониторинге технического состояния робота, в ходе которого решается интеллектуальная задача обнаружения возможных диагностических ситуаций , связанных с выходом из строя отдельного узла. Если обнаруженная диагностическая ситуация не дает однозначного ответа на вопрос, какой узел вышел из строя, то миссия приостанавливается; в соответствии с базой знаний выполняются тестовые действия для этой диагностической ситуации и анализируются их результаты. Если установлен вышедший из строя узел, то вносятся изменения в модель робота, если необходимо, вносятся изменения в систему управления роботом (например, переключение с вышедшей из строя сенсорной подсистемы на дублирующую её, если таковая имеется и работоспособна) или выполняется перепланирование миссии с учётом изменившейся модели робота.

Заключение

Автоматизация повседневной интеллектуальной деятельности и управления её качеством требует детальной разработки всех тех этапов, от которых зависит решение проблемы поддержки интеллектуальной деятельности и правильности применения знаний при этом. Первый из них - этап системного анализа, где обсуждаются требующие поддержки интеллектуальные и другие задачи, решаемые специалистами, строится схема связи этих задач [27]. При этом среди интеллектуальных задач стремятся выявить те, постановки которых известны (или выделить в них подзадачи, постановки которых известны).

Предложенная в настоящей работе многоуровневая классификация задач даёт возможность в процессе системного анализа переходить к математическим постановкам различных задач, конкретизируя те понятия и их абстракции, которые содержатся в этой классификации.

Показано, что между некоторыми задачами имеет место «генетическая связь», основанная на принципе усложнения свойств ПрО: в более сложных ПрО появляются новые виды исходных данных, которые надо учесть при решении задач (например, время, пространство, классы, причинно-следственные отношения, события или неприсущие системе внутренние процессы), и дополнительные ограничения (для различения классов сущностей обычно достаточно анализировать их признаки, а для различения диагнозов, как правило, и события).

Каждое усложнение ПрО рассматривается (в многоуровневой классификации задач) как «слой ПрО со схожими особенностями», в котором ожидается появление новых задач либо расширение постановок базового («корневого») множества задач.

Такая классификация даёт возможность увидеть задачи более общие в своих постановках и более частные, характерные для ПрО с определёнными свойствами. Поставленные в едином формализме задачи позволяют понять, в чём именно состоит каждая задача, чем она принципиально отлична от других.

Этой классификацией охвачен практически весь спектр задач, относящихся к области разработки ЭС. Вместе с тем предложенная классификация является открытой, допускающей введение в неё абстракций новых понятий, новых задач и слоёв при сохранении математического аппарата алгебраических систем, лежащего в основе классификации.

Работа выполнена при частичной финансовой поддержке РФФИ (проекты № № 15-0703193 и № 13-07-00024-а).