Ontology Partitioning: Clustering Based Approach

Published Online May 2015 in MECS

A web 2.0 is an evolution toward a more social, interactive and collaborative web, where user is at the center of service in terms of publications and reactions [1]. Today, public awareness about the benefits of using ontologies in information processing and the semantic web has increased. Since ontologies are useful in various applications, many large ontologies have been developed so far. However, large ontologies cause the following problems:

• A.    Publication : Users and applications in massive semantic web context will have to find a way to limit their ontology because otherwise it will be too big and mostly irrelevant for any single task [2].

• B.    Maintenance : Large ontologies are usually created and maintained by a group of experts and not a single person [3] such as NCI-Thesaurus [4], GALEN [5] and Gene Ontology [6]. Therefore, experts are responsible only for the part they have created.

• C.    Validation : When dealing with large ontologies, it is often difficult to understand the model as a whole [7]. After partitioning these large ontologies, validation could be done based on single modules that are easier to understand. Checking the consistency and completeness of subtopic is easier and possible.

• D.    Processing : Large ontologies could cause serious problems in processing. The complexity of reasoning on ontologies is critical even for small ontologies. Moreover,

modeling and visualization tools are unable to deal with large ontologies.

• E.    Security (access control): Sometimes some parts of ontology are not public and should be accessed only by privileged people.

Partitioning the ontology can dramatically improve the solutions to above problems [7].

With awareness of ontology capabilities in processing semantic web information, the number of ontologies has been increasing over the past decade. However, there are still some difficulties in working with ontologies having large sizes (that is having considerable amount of concepts and relationships) resulting from high time and space complexity of the processing involved. To overcome these problems, some researchers tend to use clustering and fragmentation techniques for partitioning the ontologies into meaningful parts called sub-ontology. Such partitioning can be used to process sub-ontologies locally and then combine them to gain final results.

Query answering is the primary operation of the semantic web. If the database to search for answer is a single large ontology, time taken for searching will be more. However, if the ontology is partitioned into sub ontology and indexed properly, the semantic web will only process sub ontology related to the query and hence retrieving answer will be faster.

Due to the distributed and decentralized semantic web, the ontologies of same or overlapping fields can be constructed by various experts leading to heterogeneity among ontologies. The ontology matching technique is an effective method to establish interoperability among these heterogeneous ontologies. With this in mind, Rector et al. [8] present the following goals for ontology modularization:

• A.    Scalability . This is concerned with the scalability of Description Logic (DL) reasoning. In general, the performance of DL reasoners degrades as the size of the ontology grows. Thus, there is a motivation to reduce the size of the ontology that needs to be reasoned over to that which is necessary, i.e., an ontology module. The scalability issue also concerns the evolution of the ontology, the aim being to localize the change within an ontology module.

• B .    Complexity Management. With human designed ontologies, it becomes increasingly difficult to control the accurateness of the ontology. Ontology modularization allows the designer to focus only on the relevant portion of the ontology.

• C.    Understandability. Intuitively smaller modules are easier to understand than larger ones. This is the case for both humans and agents.

• D .    Reuse. This is common practice in software Engineering and Ontology Engineering would benefit from such an approach. This goal emphasizes the need for mechanisms to produce modules in such a way that increases their chances of being reused; i.e., they only contain what is relevant and useful.

In this work, the goal of our ongoing research is to adapt, define and implement ontology partitioning based clustering approach that provides definition of set of partitions in the domain of ontology clustering. The approach is a revision and an improvement of the standard K-means clustering algorithm in two dimensions. On one hand, a new semantic similarity measure is used [9], which is an amelioration of the structure similarity of Wu and Palmer [10], in conjunction with the revision K-means algorithm to provide more accurate assessment of the similarity between concepts. On the other, the behavior model is modified to pursue better algorithmic performance.

• A. Motivations and Contributions

• 1.    Our approach is motivated by the observation that essentially, many existing clustering methods are based on the application of similarity measures defined over a fixed set of attributes of the domain objects. Classes of objects are taken as collections that exhibit low interclass similarity (density) and high interclass similarity (density). Often the second step of the traditional algorithm of K means consists to put any initial partition that classifies the data into k clusters. In this context, we have eliminated this random at the beginning of our algorithm to overcome the aforementioned limitations.

• 2.    We have observed that the adoption of the traditional algorithm of K-Means and his application in the field of ontology clustering gives a set of insignificant clusters with two or three concepts. In addition, the obtained clusters are dynamic, i.e., their content change after every execution of the algorithm with same parameters. To overcome these limitations, we have proposed an enhancement of the traditional algorithm of K-means to consider only clusters that contain significant concepts

• 3.    In this work a novel algorithm with a new semantic similarity measure are introduced, which, to the best of our knowledge are applied for the first time in the domain of ontology clustering. The proposed algorithm achieves significant improvements and shows good results with the new similarity measure compared with the others approaches.

• 4.    This paper details the principles underlying of several techniques for ontology modularization, approaches for ontology partitioning and ontology clustering. Comparison between our revision approach for ontology clustering and the traditional approach is established.

The remainder of the paper is organized as follows: Section 2 discusses issues related to ontology modularization and reviews the existing approaches. In section 3, the standard algorithm of K-means is presented, as well as different similarity measures. In section 4, we outline the proposed approach and discuss the detailed steps. Section 5 introduces an experimental methodology to evaluate the approach. Finally, we conclude this paper and outline our future work in section 6.

• II.    Ontology Modularization

In semantic web world, there exist ontologies with large number of entities that bring many problems and challenges to web extenders because of their complex and time consuming processing. According to Sellami et al. [11], clustering and fragmentation approaches are optimization techniques to work on these ontologies, because in many cases it’s better that ontologies are partitioned to small dense parts and processing is performed on those parts.

Ontology modularization can be split into two distinct tasks:  ontology partitioning and ontology module extraction. Ontology partitioning divides an ontology into a set of subsets with each subset being termed a partition, whilst ontology module extraction extracts a subset of an ontology. It should be noted that ontology module extraction is not the focus of our study.

Ontology partitioning can be used in applications such as ontology alignment, ontology merging and ontologybased text summarization [12]. Ontology partitioning is usually applicable for dividing large ontologies and acting on sub-ontologies to increase the performance of algorithms’ execution time or even for making processing on such ontologies practical.

Ontology partitioning is the task of splitting O into a set of, not necessarily disjoint, modules M= {M1, M2,..., Mn}. The union of all the modules should be equivalent to the ontology O that was partitioned {M1 ∪ M2 ∪ ... ∪ Mn} = O. Thus, a function partition (O) can be defined as follows:

Definition (Ontology partitioning Function)

Partition(O) → M = {{M1, M2,  , Mn}| {M1 ∪ M2... ∪ Mn} = O}

Stuckenschmidt and Klein [13] present a method for automatically partitioning ontologies based on the structure of the class hierarchy. The underlying assumption of the approach is that dependencies between concepts can be derived from the structure of the ontology; as such the ontology is represented as a weighted graph O=(C, D, W) where nodes (C) represent concepts and edges (D) represent links between concepts that represent different kinds of dependencies that can be weighted (W) according to the strength of the dependency. The dependencies are based on the representation language, but include features such as subclass relations between concepts. In this study, it is shown that clustering is done based on this assumption: “Dependencies between concepts can be derived from the structure of the ontology”; so a dependency graph is built by extracting dependencies resulted by subclass hierarchy and dependencies resulted by the domain and range restrictions on properties. Next, a weight is assigned to each dependency. These assignments are repeated until all of the weights are fixed. In partitioning step, this method uses a modularization algorithm called “island”: a set of nodes are located in a line island if and only if they have formed a connected sub-graph and the edges inside the island are stronger than edges existing in the island.

Cuenca Grau et al. [14] address the problem of partitioning an OWL ontology (O) into an E-Connection. E-connections [15] allow the interpretation domains of combined system (here each system can be seen as a description logic knowledge base) to be disjoint, where these domains are connected by means of n-ary ‘link relations’. These ‘link relations’ allow connections to be drawn between the different partitions, as such reasoning can be done over a combination of linked partitions.

Kutz et al. [15] Show that Distributed Description logics [16] are a special case of E-connections linking a finite number of DL knowledge bases. The partitions produced by [14] are both structurally and semantically compatible. Structural compatibility ensures that no entities or axioms are added, removed or altered during partitioning; that is every axiom that exists in the E-connection also exists in the ontology. Semantic compatibility is a desirable relation between the input and the output of a partitioning process as it ensures that the interpretation of the ontology with partitions is equivalent to the interpretation of the ontology without partitions.

In [17], the importance and requirement of large-scale ontology partitioning by various semantic web operations is discussed. Further, a brief outline of the existing system that partitions the large ontology is also presented. Partition algorithm to decompose large ontology into set of partitions is proposed. The partition algorithm is designed to increase the efficiency compared to the existing ontology partition algorithms. This goal is achieved by reducing the number of computation needed for the neighbor similarity and merging the partitions ontologies.

The introduced approaches in this area do partitioning in one of two ways: some of them use modularization techniques and others use graph-clustering techniques.

In a study by Kolli [18], the graph representation for clustering an ontology is traversed in a breadth-first manner starting from the root and collected MB number of nodes within a subset (2*MB is the total number of nodes that can be held in main memory); Next, each subset is expanded to covering its neighbors. The goal of this approach is just dividing ontology to make further processing on it practical.

In the study carried out by Hu et al. [19], the clustering done on the graph was constructed based on dependencies caused by subclass hierarchy. In this approach, a weight is assigned to each dependency by using the linguistic and structural information of entities. After weighting links, the ROCK algorithm is used [20] (it is an agglomerative clustering method) for graph partitioning. In final step each cluster is expanded to a group of entities called block.

Schlicht and Stuckenschmidt [21] extended this approach with the addition of two steps after producing islands: merging (merge similar islands) and axiom duplication (copy axioms in adjacent islands). These two steps have improved results a little.

In the study carried out by Huang and Lai [22], they acted on edge-by-node matrix of ontology graph (also called incidence matrix). Here, the similarity value between two entities is partly determined by the number of edges common between them. In partitioning step, this approach uses KNN (k nearest neighbors) algorithm. After assigning all of the nodes, clusters with high similarity values are merged together.

The approach introduced by Cuenca et al. [23] has n stages in which n are the number of entities in the ontology. In each stage a decision is made about one entity and if it and its relations can be transferred to a cluster or not; so in each stage, one entity might be transferred to another cluster or might be left in the initial cluster. This type of partitioning is also done in polynomial time.

The approaches of Kunjir and Pujari [24], a review is done on techniques to calculate clusters similarity on point sets domain so that they can easily adopt such a technique for calculating clusters similarity in ontology graphs.

In [25] the authors proposed a structural-based ontology partitioning approach with time complexity. This approach is completely automated and one of its advantages is its ability to produce a predefined number of partitions. In other words, it can produce clusters in each level of granularity which is beneficial in some cases. Evaluation results of the approach shows that it can produce meaningful clusters with relatively balanced sizes. (n2).

In [26] the partitioning of data using ontology relations in PHC domain was discussed and illustrated. Few tables like contributed-attribute table, concept table and link tables were built to implement CBRO (clustering based on relational ontology) for the PHC domain (Preventive health care domain. First, data was clustered in concept level. Second based on the existing ontology relations other new relations are generated through this process. Ontology relations are derived between two concepts by implementing CBRO application in PHC domain (Data base). Finding semantic correspondences among multiple attributes is significant in many applications, such as schema integration.

In [27], the authors employ the k-means clustering algorithm to perform schema matching among multiple attributes, which is more difficult than find pair wiseattribute correspondences. They first convert attributes into points, then use k-means to partition the attribute points into different clusters. The attributes in the same cluster have the similar semantics. In the clustering process, they randomly choose k objects as the initial centriods. After that, they employ the TFIDF weighting method and the vector space model to be as the metric of the distance between attributes points. Finally, they perform extensive experiment.

In [28], the authors presented a new family of measures that is suitable a wide range of languages since it is merely based on the discernability of the input individuals with respect to a fixed committee of features represented by concept definitions. Such as the new measures are not absolute, yet they depend on the knowledge base they are applied to. Thus, also the choice of the optimal feature sets deserves a preliminary feature construction phase, which may be performed by means of a randomized search procedure based on simulated annealing.

The work of [29] proposes a method of directing content by clustering ontologies. By defining a special formula to calculate the similarity. The aggregation tree created has good semantic explanation. They apply then this method on the cache and present a new ACR cache system.

• III.    Traditional Partitioning Clustering Algorithm and Similarity Measures

K-means is the most popular traditional partitioning clustering algorithm for text documents. The K-means algorithm begins by initially selecting K random seeds in the document search space. These K points are assumed to represent centroid of the K initial clusters. The algorithm then calculates the distance (or similarity) of each document from all the K points. These distance values are used to assign every document to one of the K clusters. A document is assigned to a cluster which is closest to it i.e. the cluster whose centroid has the smallest distance from the documents, out of all such K centroids. Once all documents are assigned to one of the K clusters, the centroids of all the K clusters is recomputed. The process is iterated with the new centroids as new cluster centers which is repeated until cluster assignment converges or until a fixed number of iterations has been reached. For more detail, see [30]. Inspite of different algorithms being proposed for efficient document clustering, research in the domain of ontology clustering is still at its dip. A few works applying K-means approach exist in the field of ontology clustering. For this raison, we have adopted a revised approach of K-means to produce a set of clusters from domain ontology. As K-Means is unstable and quite sensitive to the selection of initial seeds, we propose two solutions to overcome these problems. In our work, we introduce an algorithm for ontology clustering based on the calculation of different similarity measures.

The next section outlook the different major similarity measures used in our work.

• A. Different Similarity Measures

The proposed ontology clustering using K-means approach combines semantic weighting by calculation of similarity measures. A brief literature study is proposed in this section of different similarity measures applied in our work.

This measure is defined by the common objects number divided by the objects full number minus the common objects number.

.X ∗ У

Sim) ⁽ X , Y )=_‖‖2  ‖‖5------

‖‖ +‖‖ - ∗

Such as x and y are there vectors extracted starting from the concepts C1 and C2. || x ||= Ω ^x i=1 indicate the vector normalizes X.

‖ x ‖2

=√∑

| Xl |²

Cosine

It uses the complete vector representation, i.e. the objects frequency (words). Two objects (documents) are similar if their vectors are confused. If two objects are not similar, their vectors form an angle (X, Y) whose cosine represents the similarity value.

X ∗ У

SimC ( X , Y )= COS ( X , Y )=_‖‖2   ‖‖2      (3)

‖‖ +‖‖

Euclidean

It’s based on the ratio of the Euclidean distance increased by 1. The Euclidean distance is defined by the following formula: dE =‖ X - у ‖²

SimE ⁽ Ci , C2 )=                              (4)

1+

Dice

It’s defined by the number of the common objects multiplied by 2 on the full number of objects. Like the Jaccard similarity, the Dice also measures set agreement. In this case, the measure is given by the formula.

2∗ X ∗ У

SimD ( Ci , Сг )=   2 —iTH

_‖‖ +‖ У ‖2

• 2) Techniques Based on the Arcs

The most intuitive similarity measurement of the objects in ontology is their distances [33] [34] [35]. Obviously, an object X is more similar to an object Y than an object Z; this similarity is evaluated by the distance that separates the objects in ontology. Among the work classified under this banner, we can cite Palmer [10] has the advantage of being simple to implement and have good performances.

Wu and Palmer Measure

This measure was used in organizing web documents in clusters [10]. It was also useful in evaluating the semantic proximity of two concepts of a HTML page relative to a thesaurus within the framework of a Web site indexing by ontology. It’s based on the following principle (To see the face nearby): Given ontology O formed by a set of nodes and a root node (CR).

C1 and C2 represent two ontology elements for which we will calculate the similarity. The principle of similarity computation is based on the distances (D1+DR) and (D2+DR) which separate the C1 and C2 nodes from the node CR and the distance (DR) which separates the subsuming concept or the smallest generalizing of C1 and C2 of node CR. This measure is applied in our work.

• 2 ∗ DR

SimWP( C1, C2) =                          (6)

D1 + D2 + 2 ∗ DR

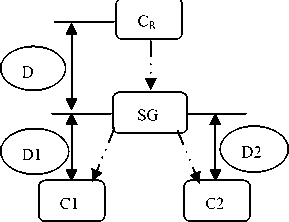
Fig. 1. Example of an ontology extract.

The new measure that is inspired from the advantages of [36] work, whose expression is represented by the following formula:

2∗

Sim     (  1,  2) =          ∗    ( 1,  2)      (7)

Let PF (C1, C2) be the penalization factor of two concepts C1 and C2 placed in the neighborhood.

PF(C1,C2)=(1-X)(Min(N1,N2)-N)+X(N1-N2|+1)-1 (8)

Let N1 and N2 be the distances that separate nodes C1 and C2 from the root node, and N, the distance that separates the closest common ancestor of C1 and C2 from the root node. C1 and C2 are the concepts for which the similarity is computed.

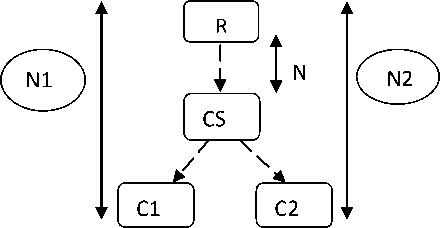
Fig. 2. Example of an ontology extract

Dennai Measure

Sim (  1,2)

2∗D

1+ 2+2∗  +     ( ,)

(    ,)

Г0 if C1 is anesttor of C2 оr convereely I D ist if C 1 and C2 ree close d by a CS

Where = ( + 1) ∗ ( + 2) and FPD_SG (Function Produces Depths by Smaller Generalizing) is a function that makes it possible to penalize the similarity of two close concepts that are not located in the same hierarchy. In the case of close concepts, FPD_SG gives the distance of many arcs equal to the product of depths of the two concepts compared to the ontology root while passing by a CS. More and more that the distances D or Di (where D is the distance between CS and the root and Di represent the distance between a concept Ci and it CS) are moved away, more and more SimDB decreases. With this function, the similarity measurement between two hierarchical concepts is higher than the similarity between two close concepts by a CS.

• IV.    The Proposed Approach

In this section, we outline the different steps of our approach (see Fig. 3).

• A.    Preprocessing

In order to carry out our approach, at first, the system extracts all constructors from the OWL ontology file: (.i.e., Classes, axioms, taxonomic and non-taxonomic relations and properties). The constructors of OWL are included between tags, as consequence, tags are polluted and need to be cleansed. Therefore, the OWL ontology file is analyzed and cleaned using an algorithm of cleansing to conserve only the useful information. Finally, the API Jena and the Ontology module extractor (OME) are used to extract the different type of constructors.

• B.    Creation of level graph

Graphs are useful for representing many problems in computer science and in the real world. Finding out whether a node is reachable from another node, to the extremely complex, such as finding a route that visits each node and minimizes the total time. A common, but solvable problem is that of problem of simple path finding. Generally, the task is determining the shortest path from a given node to any other node on the graph.

Dijkstra's algorithm is one of the most common algorithms that solve the problem of finding shortest paths from a particular source node to any other node where no edge has a negative weight. The figure 4 shows the ontology graph node.

Preprocessing

(Extraction of different constructors of owl)

Input : Owl ontology

OWL constructors: Extracted classes, relations and properties

Level graph Incidence matrix

-►

Distance matrix

Validated

Clusters

Validation Process

Modelization (Creation of node graph)

Distance between concept and root

Output :

I*

Clusters

Similarity measures’s

Matrixs

Clustering Process

Fig. 3. Different steps of our approach.

Similarities measures

Computing

Fig. 4. Screenshot of the graph node

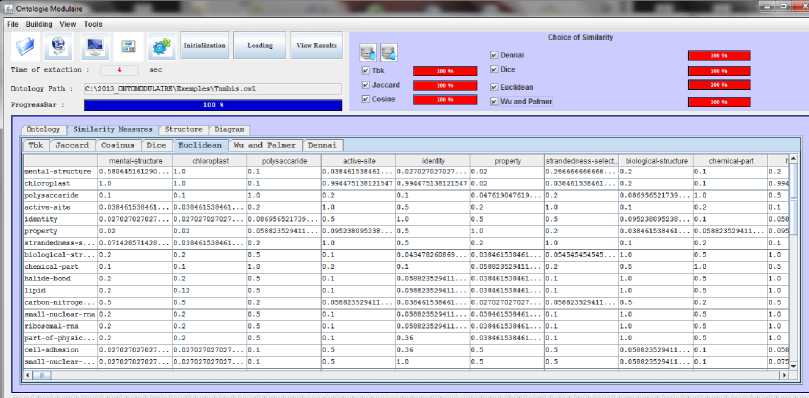
Fig. 5. Screenshot of the similarity measures computing

• C.    Similarity measures Computing

In this step, we calculate the different similarity measures from a given node to any other node on the graph based. Besides the similarity measure [9], we implemented the formula of six similarity measures (Tbk, Jaccard, Cosine, Dice, Enclidian, and Wu and Palmer). The task is determining the shortest path from a given node to any other node on the graph. This step generates the different matrix of similarity measures (see Fig. 5).

• D.    Clustering Process

Our Ontology clustering problem can be formally defined as below. Given:

• (i ) a set of concepts of the ontology O = {C1, C2,…, CN},

• (ii ) a desired number of clusters k, and

• (iii ) an objective function f that evaluates the quality of a clustering.

We want to compute an assignment γ : O → {1, . . . , K} that minimizes (or, in some cases, maximizes) the objective function. Mostly, γ is surjective (i.e. none of the K clusters is empty). The objective function is often defined in terms of a similarity measure or distance measure.

The intuition of clustering is that objects in the same partition set should be close or related to each other. For our ontology, we use two algorithms.

First, a conventional K-means algorithm (Algorithm 1) was introduced for adapting the traditional algorithm to ontology clustering. After that the algorithm is modified to integrate the different similarity measures

Algorithm1:  Adaptation Algorithm of K-Means

Approach to ontology clustering

Inputs nb_cluster, nb_iter_max, n

Output nb_cluster

BEGIN h = 1

While (h < nb_iter_max) and (fin = false) Do

//loop for nb_iter_max

Begin

For i = 0...n Do //for each concept of ontology

Begin

For s = 0...nb_cluster Do

Begin center[s].weight = |concept[i]. weight - center[s].weight | End min = center [0].weight ind=0

For s = 0...nb_cluster Do

Begin

If center[s] .weight < min Then

Begin min = center[s]. weight ind=s

End

End concept[i].cluster = ind module[i] = ind

END center_x = 0 nbx = 0 cond = true

For s = 0...nb_cluster Do //compute the new center

Begin center_x = 0 nbx     = 1

For i = 0...n Do

Begin

If concept[i].cluster = s Then

Begin center_x = center_x + concept[i].weight nbx = nbx +1

End

End center[s].weight = center_x / nbx // div (center_x, nbx).quot

If center1[s]. weight <> center[s] .weight Then cond = false

End

If cond Then fin = true;

Else

Begin

For i = 0...nb_cluster Do center1[i] .weight = center[i]. weight

End h = h +1

End While

Output= nb_cluster {C1,C2,……,Ck}

END

Second, we eliminate the unnecessary generated clusters with minimum and insignificant concept. In Algorithm 2, the adapted K-means algorithm is executed with a maximum number of clusters as input, to compute the optimum numbers of clusters. If at last one cluster whose size is smaller than the value of threshold, then this cluster will be overlapping and will be removed with other clusters and decrease the K_max to K_max-1. If it is not the case, visualize the number of clusters with their content and their size.

Algorithm2: Revision Algorithm of K-Means Approach Inputs max_ nb_clusterx, threshold

Output optimal_number_of_cluster

BEGIN

• 1.    Run algorithm K_means with Max_ nb_cluster

• 2.    Compute the number of clusters

• 3.    If at last one cluster has size < threshold Then

• 4.    Begin

• 5.    max_ nb_cluster = Max_ nb_cluster -1

• 6.    goto 1

• 7.    end

• 8.    Else Visualize the number and the size of clusters

• 9.    Output=optimal nb_cluster{C1,C2,……,Ck}

END

• E.    Validation Process

After the partitioning process, the obtained partitions should undergo a validation process that needs to be performed for each cluster. This process can be solved in future work by using reasoning tool like pellet.

• V.    Experimental Evaluation

We have performed two sets of experiments. In the first one, we used the TAMBIS ontology, which contains nearly 393 classes related by subsumption links, and 597 axioms that describe both molecular biology and bioinformatics tasks. The second experimentation was made on photography ontology of that contains 185 classes, 268 relations and different type of object and data type properties.

We noted that the both analysis and extraction of the OWL constructors of the two ontologies by our system were performed in 30 and 20 second respectively.

• A.    Evaluation Measures

In this paper, cohesion and density evaluation methods are adopted although there exist many evaluation methods currently and the terms cohesion and density. Cohesion refers to the degree of the relatedness of OWL classes, which are semantically/conceptually related by the properties relatedness of elements in ontologies (relatedness of elements in ontologies.) Density is defined as the presence of clusters of classes with many non-taxonomical relations holding between them.

• B.    Experimental Results

In this section, some experimental evaluations of proposed approach are presented. All of the tests are carried out on an Intel Core TM 2 Duo 2.00 GHz laptop with 2 GB memory under Windows 7 operating system and Java Netbeans 7.1.1. We report the results for our experiment by highlighting for each step the evaluation values metrics.

Experiments were made on Tambis ontology for K-max=40 and Threshold =5. The obtained results are depicted in Fig.6. and Fig.7. and summarized in Table 1.

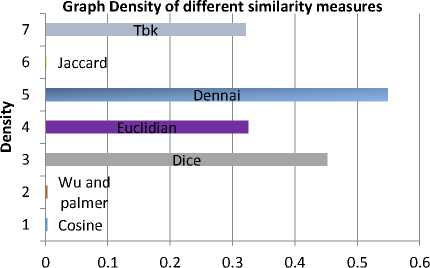
Fig. 6. Graph Density of different similarity measures for Tambis ontology

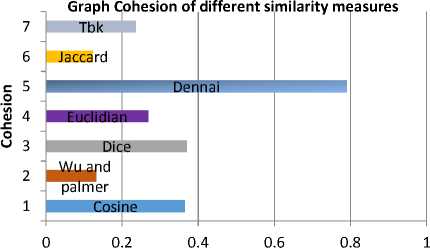
Fig. 7. Graph Cohesion of different similarity measures for Tambis ontology

Table 1. Experiments of Tambis ontology for K-max=40 and Threshold =5.

Measures	Number of partition	Threshold	Number of iteration	Cohesion	Density
Cosine	2	5	100	0,365	0,003
Wu/palmer	2	5	100	0,133	0,003
Dice	3	5	100	0,370	0,452
Euclidian	3	5	100	0,269	0,325
Dennai	4	5	100	0,790	0,549
Tbk	5	5	100	0,237	0,321
Jaccard	6	5	100	0,124	0,002

Other experiments were made on Photography ontology for K-max=50 and Threshold =7. The obtained results are depicted in Table 2.

Table 2. Experiments of Photography ontology for K-max=50 and Threshold =7.

Measures	Number of partition	Threshold	Number of iteration	Cohesion	Density
Cosine	4	7	100	0,365	0,005
Wu/palmer	3	7	100	0,032	0,203
Dice	4	7	100	0,321	0,459
Euclidian	4	7	100	0,321	0,321
Dennai	6	7	100	0,856	0,655
Tbk	2	7	100	0,137	0,004
Jaccard	3	7	100	0,325	0,005

In addition, other experiments were made on the    respectively. The obtained results are depicted in Fig.8. and ontology Tambis for K-max=30, 20 and Threshold =10, 7   Fig.9., respectively.

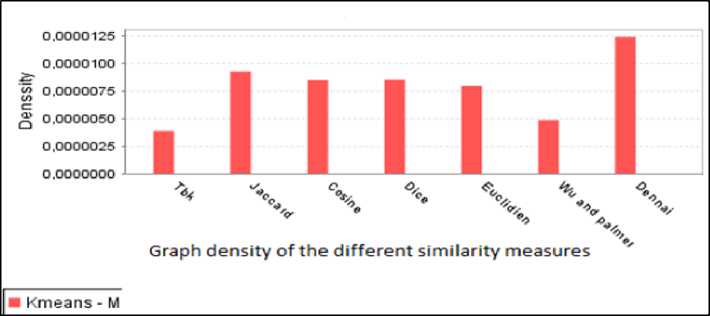
Fig. 8.Graph Density of different similarity measures for Tambis ontology

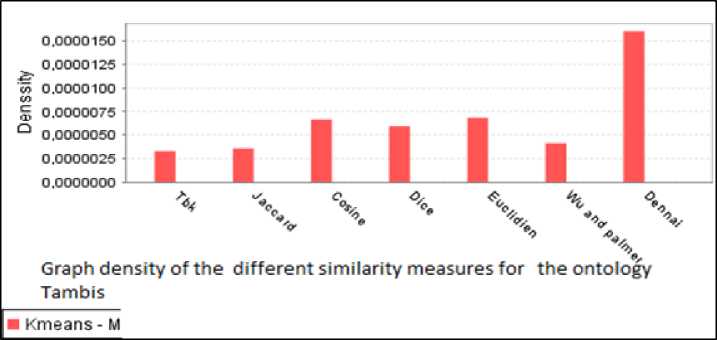
Fig. 9. Graph Density of different similarity measures for Tambis ontology

The results of the two experiments prove that Dennai’s measure gives more and better results of partitions comparing with the six others measures.

The Fig.10. reports the results of the ontology Tambis. In this experiment, we compare the traditional algorithm of K-means (Kmeans_S) with our revised algorithm (Kmeans_M) for K-max=30 and Threshold =10.

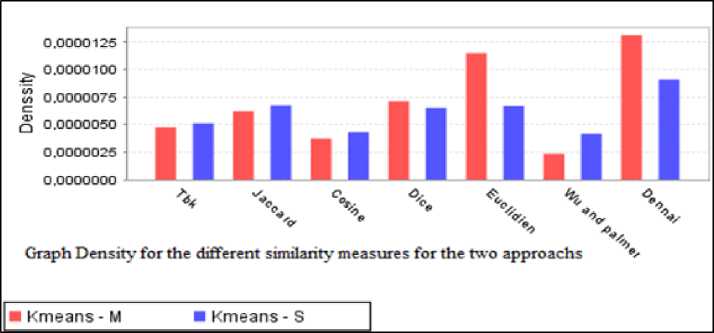
Fig. 10. Graph density for the two approaches for the different similarity measures

To have a wider comparative view, we run at first the traditional K-means algorithm fourfold with the ontology Tambis. We have affirmed that the algorithm gives different numbers of clusters with the same parameters and the content of every cluster is dynamic and change, and sometimes one cluster contains only the center concept, two or three concepts in some cases. This is big problem, our revised algorithm overcomes this limitations, its proves for the four run that the content of every cluster is fixe and in all cases there is any cluster which contains unnecessary classes because we had introduce the value parameter threshold. Further, the novel measure gives the better result in term of density compared to the others similarities.

• C.    Discussion

For evaluating and measuring the quality of the generated clusters by our clustering approach, we use two design metrics that are cohesion and density. To have a wider comparative view, we run successively the traditional and the revised K-means algorithms with the two ontologies.

As we have affirmed above, the traditional algorithm often gives a set of insignificant clusters with two or three concepts. Our revised algorithm overcomes this limitation by returning only clusters that contain significant concepts (.i.e., whit high cohesion and density). While comparing the traditional and the revised K-means algorithm based on the seven similarities measures, we conclude that the Dennai’s measure produces higher qualitative clusters in all of cases.

• VI.    Conclusion and Future Work

Ontology partitioning is a good solution to overcome challenges of large ontologies such as reusability, scalability, complexity and maintenance. Ontology partitioning is motivated by the problem of dealing with large and very complex ontologies by decomposing them into modules. The problem is that processing large ontologies consumes more time and space than processing only parts of ontologies. In this paper, we propose an adaptation and a revision of the traditional K-means algorithm to partition OWL ontologies based on novel semantic similarity measure.

Experimental results shown that our approach reduces required time and space to process an ontology and produces high quality partitions (.i.e., with high cohesion and density). The revised K-means algorithm using the proposed Dennai’s similarity measure provides better partitions and meaningful clusters than the traditional K-means algorithm.

For evaluating and measuring the quality of the partitions produced by our clustering approach, we project testing other external validity measures like precision, recall and F-measure. Moreover, we plan validating the obtained clusters according to others design metrics, like coupling and modularization quality. Ongoing work concerns the use of the proposed algorithm of ontology clustering in query answering and matching. Finally, future work also will be to test the novel proposed semantic similarity measure on other real and more complex ontologies.