OpenMP Teaching-Learning Based Optimization Algorithm over Multi-Core System

Published Online June 2015 in MECS

Optimization, in simple terms, means minimize the cost incurred and maximize the profit such as resource utilization. EAs are population based metaheuristic (means optimize problem by iteratively trying to improve the solution with regards to the given measure of quality) optimization algorithms that often perform well on approximating solutions to all types of problem because they do not make any assumptions about the underlying evaluation of the fitness function. There are many EAs available viz. Genetic Algorithm (GA) [1] , Artificial Immune Algorithm (AIA) [2], Ant Colony Optimization (ACO) [3], Particle Swarm Optimization (PSO) [4], Differential Evolution (DE) [5], [6], Harmony Search (HS) [7], Bacteria Foraging Optimization (BFO) [8], Shuffled Frog Leaping (SFL) [9], Artificial Bee Colony (ABC) [10, 11], Biogeography-Based Optimization (BBO)

[12], Gravitational Search Algorithm (GSA) [13], Grenade Explosion Method (GEM) [14] Firefly (FF) [15], [16] etc. To use any EA, a model of decision problem need to be built that specifies the decision variables, objective and constraints. These 3 parameters are necessary while building an optimization model. The solver will find values for the decision variables that satisfy the constraints while optimizing (maximizing or minimizing) the objective. But the problem with all the above EAs is that, to get an optimal solution, besides the necessary parameters. Various algorithms are parameter specific and that parameters need to be handled separately. For example, in case of GA, adjustment of the algorithm-specific parameters such as crossover rate, mutation rate, crossover type, type of encoding etc. affects the optimal solution obtained. Thus, in all the above EAs, selection of algorithm-specific parameter’s value affects the optimal solution obtained. But in TLBO, there are no algorithm-specific parameters.

TLBO has been an efficient metaheuristic technique recently developed, for solving optimization problems with less computational effort and high consistency. Its advantage over other EAs is that, it has no algorithmspecific parameter (parameter less). The TLBO algorithm, which was proposed by Rao (2011), is actually based on the philosophy of teaching and learning. In a classroom, the teacher is considered as a highly learned person who tries to improve the outcome of learners by sharing his/her knowledge with them. It is called the Teacher phase of TLBO. Also, learners share and learn from the interaction among them, which help to improve their outcome. It is referred to as the Learner phase of TLBO [17]. In the entire process, TLBO tries to shift mean towards best.

Nowadays, multi-core CPUs (Central Processing Unit) are getting more and more common and cheaper. One cannot ignore their importance anymore. With the recent advancement of multi-core system, researchers have been modifying EAs for parallel implementation on a multicore system. The multi-core systems can run multiple instructions simultaneously on multiple cores; it increases overall speed for programs [18].

While using multi-core system, the improvement in performance depends upon the algorithms used and their implementation. In particular, possible benefits depend upon (or limited by) the fraction of the algorithm that can be managed in parallel on multiple cores simultaneously; this issue is explained in Amdahl's law. The problems which are embarrassingly parallel may realize speedup factors near to the number of cores. Even more speedup factors can be realized by splitting up the problem so that it can fit within the cache of each core(s), thereby avoiding use of much slower main memory of the system. In order to accelerate performance of application, programmers have to work more on re-factoring the whole problem. The parallelization of algorithms on a multi-core the system is a significant ongoing topic of research.

Recent advancement in High Performance Computing (HPC) have seen the usage of many cores of multi-core system (viz. i3, i5, i7 etc.) for solving computationally intensive task parallelly. OpenMP is an API for writing shared-memory parallel applications in C, C++, and FORTRAN. With the release of API specifications (in 1997) by the OpenMP Architecture Review Board (ARB), use of CPU’s computational power (in particular, multiple cores of multi-core CPU) for parallel computing has become easy [19]. OpenMP is ideally suited for multi-core architectures hence it allows programs to be parallelized incrementally with little programming efforts.

The designers of OpenMP developed a set of compiler pragmas, directives, and environment variables, function calls which are platform-independent. In application exactly where and how to insert threads are explicitly instructed by these constructs. Most of the loops can be parallelized just by adding #pragma_omp_parallel_for before the ‘for loop’ construct in C. The main tasks while using OpenMP are 1) to determine which loops should be threaded and 2) to restructure the algorithms for maximum performance. The OpenMP provides maximum performance, if it is applied to threads in the application which are most time-consuming loops.

Thus, if the bottlenecks in the algorithm are identified and modified suitably, using OpenMP, one can easily exploit the functionality of multi-core system and can maximize the utilization of all the cores of multi-core system which is necessary from the optimization point of view (for example, maximize the resource utilization). This paper contributes towards this direction and undertakes a detailed study by investigating the effect of number of cores, dimension size, population size, and problem complexity on the speedup of TLBO algorithm. In the remainder of this paper, we give a brief literature review of TLBO and its applications. Thereafter, we discuss the possibilities of tweaking a TLBO to make it suitable for parallel implementation on a multi-core system. Then, we present results on a few test problems of different complexities and show appreciable speed-ups using our proposed algorithm.

• II.  Literature Review

TLBO is very effective than other metaheuristics because of its characteristics viz. parameter less, high consistency, and less computation effort. It outperforms some of the well-known metaheuristics regarding constrained benchmark functions, constrained mechanical design [20], and continuous non-linear numerical optimization problems [17], it is being used by various researchers as a replacement for the other EAs available. Such a breakthrough has steered Cˇrepinšek et al. [21] towards investigating the secrets of TLBO’s dominance. They investigated some mistakes regarding TLBO through code-reviews and experiments respectively. However, Waghmare in [22] commented on the work of Cˇrepinšek et al. He not only addressed the queries raised by Cˇrepinšek et  al.  but also re-examined  the experimental results, which demonstrates that the TLBO algorithm performs well on the problems where the fitness-distance correlations are low by proper tuning of the common control parameters of the algorithm, and corrected the understanding about the TLBO algorithm in an objective manner. TLBO has been used by number of researchers to solve their problems and found it effective than other Metaheuristic. Krishnanand et al. in [23] have applied a multi-objective TLBO algorithm with nondomination based sorting to solve the environmental or economic dispatch (EED) problem containing the incommensurable objectives of best economic dispatch and least emission dispatch. Rao and Patel in [24] explored the use of TLBO and ABC algorithms for determining the  optimum  operating  conditions of combined Brayton and inverse Brayton cycles. Rao et al. in [25] proposed the optimization of mechanical design problems using TLBO and tested it on five different constrained benchmark test functions with different characteristics, four different benchmark mechanical design problems and six mechanical design optimization problems. González-Álvarez et al. in [26] proposed Multi-objective TLBO (MO-TLBO) for solving Motif Discovery Problem (MDP) and solved a set of twelve biological instances belonging to different organisms. Rao and Patel introduced and investigated the effect of elitism on the performance of TLBO algorithm while solving complex constrained optimization problems [27] and unconstrained benchmark problems [28]. Population size and Number of generation, these parameter affects the performance of TLBO are also investigated. Rao and Kalyankar in [29] made an attempt to achieve conflicting objectives by finding optimum parameter settings for the LBW process by applying TLBO for parameter optimization of the LBW process. Rajasekhar et al. in [30] proposed a new variant of TLBO, termed as Elitist Teaching-Learning Opposition based (ETLOBA) Algorithm for numerical function optimization, which is empowered with two mechanisms, one is elitism and second is Opposition method (helps to improve the capability of searching), to reach the accurate global optimum with less time complexity. Rao and Patel in [31] introduced a modified version of the TLBO algorithm and applied the same for the multi-objective optimization of heat exchangers. Pawar and Rao in [32] presented TLBO to find the optimal combination of process parameters of the abrasive water jet, grinding and milling machining processes. Rao and Kalyankar in [33] applied TLBO for the process parameter optimization of electrochemical machining (ECM) process and electrochemical discharge machining (ECDM) process. Rao et al. in [34] proposed TLBO to solve continuous unconstrained and constrained optimization problems. Niknam et al. in [35] proposed a θ-multi-objective-TLBO algorithm to solve the dynamic economic emission dispatch problem.

• III.  Algorithm

Most of the times TLBO uses only single core of multi-core system thereby leaving other cores idle. One of the goals of optimization is to maximize the profit such as resource utilization, so it’s necessary to make algorithm parallel either by design or programming way, which exploits all the cores of multi-core system and maximize the CPU utilization. OpenMP maps threads onto physical cores of CPU, hence all the OpenMP threads run in parallel and provide more optimal solution in less amount of time thereby providing speedup compare to Simple TLBO (STLBO). The basic TLBO algorithm can be stated as in fig. 1.

begin

Best = pop[1] {optimal} Index = 1

for (i= 2 to pop_size)

if Fitness(pop[i]) is better than Fitness(pop[1]) Best = pop[i] Index = i endif end for

Best_Solution = pop[Index]

end

Fig. 1. Pseudo code of TLBO

The OpenMP algorithm exactly emulates the sequential algorithm where calculation of Fitness, calculation of mean, calculation of best, and comparison of fitness function remains same whereas small changes are introduced to achieve better result/performance.

In the following subsections, how the different functions of TLBO work, how we have parallelized them, and discuss the intricacies involved in are mentioned in the paper.

• A.    Initialize_Population

• B.    Calculate_Fitness

This method evaluates fitness of each individual of population using the defined objective function, which indicates how much each variable contributes to the value to be optimized (either maximize or minimize) in the problem. The fitness evaluation of each individual is independent step; an OpenMP parallel pragma is used to create multiple threads, ranging from 2 to 32, to evaluate each individual’s fitness separately and are mapped onto corresponding numbers of physical cores (e.g. 2 threads are mapped onto 2 physical cores. Similarly, 4, 8, 16 and 32 threads are mapped onto 4, 8, 16 and 32 physical cores respectively). It is possible to map more than one thread on a core but in practice it is best to have one-to-one mapping. In this way, this step is parallelized and reduced the overall time required to evaluate the fitness of all individuals of the population and also maximized the CPU utilization (by utilizing all the cores of the CPU). This method is called twice, once in Teacher phase and once in Learner phase (in case of elitist TLBO it is called more than twice), parallelization of this method helps significantly in reducing the amount of time required for total execution.

• C.    Calculate_Mean_Vector

This method calculates the mean of each decision variable in the population. This method is parallelized by creating multiple OpenMP threads (2 to 32) which are deployed over the multiple cores (2 to 32) of CPU (one-to-one mapping). Thus by calculating means of each decision variable simultaneously, the amount of time required to calculate mean of all decision variables is reduced and this simultaneous execution maximizes the CPU utilization as well.

• D.    Best_Solution

This method finds the best solution from the population based on its fitness value. An individual candidate solution having optimum fitness value (either minimum or maximum, as per the requirement) is termed as Best_Solution (or Teacher) and is selected to calculate new population in Teacher-phase. The simple logic applied for this method is in fig. 2.

To parallelize this method, REDUCTION (Min or Max) pragma of OpenMP can be used, but it is found that, the use of REDUCTION pragma deteriorates the performance of this method, because to select the Best_Solution, first, we need to find the optimal fitness value and its index and based on that index the candidate solution from the population is selected. This calculation of index adds overhead which deteriorates the performance. So, above simple logic is applied to avoid the reduction in performance.

AlgorithmTLBO begin g ← 0;

Initialize_Population(P, pop_size)

Evaluate(P)

{Calculate_Fitness(P)} repeat

{Teacher Phase} r = random(0 to 1)

TF = round(1 + r) {1 or 2}

Xmean←Calculate_Mean_Vector(P) Xteacher ← Best_Solution(P)

Difference_Vector = r ∙ (Xteacher -(TF ∙ Xmean))

Xnew, i = Xold,I+ Difference_Vector

Evaluate(Xnew)

{Calculate_Fitness(P)} ifXnew, i is better than Xold, i then

{Compare_Fitness(P)}

Xold, i ← Xnew, i end if {End of Teacher Phase}

{Learner Phase} ii ← random(pop_size){ii ≠ i} if Xi better than Xii then

Xnew, i = Xold, i + r ∙  (Xi - Xii)

else

Xnew, i = Xold, i + r ∙  (Xii - Xi)

end if

Evaluate(Xnew, i) {Calculate_Fitness()} ifXnew, i is better than Xold, i then

{Compare_Fitness()}

Xold, i ← Xnew, i end if {End of Learner Phase} end for g ← g + 1

until (g ≠ num_gen) {Termination_Condition}

Print_Best_Result(P)

End

Fig. 2. Pseudo code of Best Solution

• E.    Create_New_Population

Based on the values of Mean, Best_Solution, r and TF (r and TF are randomly generated), a Difference_vector is calculated and added to each individual solution of the old population to get the new population. This addition of Difference_Vector to each individual is an independent step; an OpenMP parallel pragma is used to create multiple threads (2 to 32) for performing the addition separately and are mapped onto multiple physical cores (2 to 32). Thus, by adding the Difference_Vector to each candidate solution simultaneously, the amount of time required to create new population is decreased significantly and this simultaneous creation maximizes the CPU utilization. After this, the fitness value of the new population is evaluated.

• F.    Compare_Fitness

This method compares the fitness of newly calculated population with the fitness of the old population. The fitness of each candidate solution of the new population is compared with the fitness of the corresponding candidate solution of the old population and the one with the best fitness value is selected (survival of the fittest). This one-to-one comparison is also an independent step and thus, parallelized by creating multiple OpenMP threads (2 to 32), which are mapped on multiple cores (2 to 32) of CPU. This method is also called twice, once in Teacher phase and once in Learner phase. Hence, the parallelization of this step significantly reduced the overall time required to compare the fitness of the new population with the old population and also optimize the CPU utilization.

• IV.    Test Function

In the field of optimization, it is a common practice to compare different algorithms using different benchmark problems. In this work also different benchmark problems are considered having different characteristics such as separability, multimodality, and regularity. If the function has two or more local optima then it is considered as a multimodal function. A separable function can be written as a sum of functions of variables separately. A function is regular if it is differentiable at each point of its domain. It is very difficult to optimize non-separable functions and difficulty increases if the function is multimodal. Complexity increases when the local optima are randomly distributed. Moreover, complexity increases with the increase in the dimensionality. The benchmark problems used for experimentation are shown in table 1.

• V.    Experiment Result

To validate Parallel implementation of STLBO (i.e. OpenMP TLBO) results are compared with the results of sequential STLBO algorithms for different benchmark problems existing in the literatures. Paper focuses on showing the speedup of programming parallel algorithm. The objective functions considered for experimentation are to check the algorithm’s ability to find the optimal solution.

Table 1. List of test problems

Sr. No.	Function Name	Equation	Range	F(x)	C
F1	De Jong	f ( X )=∑ xt                      \	[-5.12,5.12]	0	US
F2	Axis Parallel Hyper-Ellipsoid	f ( X )=∑ ( i . xt )	[-5.12,5.12]	0	US
F3	Sum of Different Power	f ( X )=∑| Xt |	[-1,1]	0	US
F4	Quartic	f ( X )=∑ ixt + random [0, 1)	[-1.28, 1.28]	0	US
F5	SumSquares	f ( X )=∑ ixt	[-10, 10]	0	US
F6	Zakharov	f ( X )=∑ xt +(∑0.5 ixt ) +(∑0.5 Ut ) i=l        t=l              i=l	[-5,10]	0	UN
F7	Hper Sphere	f ( X )=∑ xt                      \	[-5.12, 5.12]	0	UN
F8	Rastrigin	f ( X )=∑[ xt -10 cos (2 ПХ[ )+10]	[-5.12,5.12]	0	MS
F9	Ackley	f ( X )=-20 exp (-0.2√1 ∑ xt )- exp (1∑ cos (2 ЛХ[ )) +20+2.718	[-32.768,32.768]	0	MN
F10	Griewangk	' ( X )=40100∑ xt -∏ cos (√ i )+1	[-600,600]	0	MN

In the experimentation following system configuration is used - Intel(R) Core i7-2600 CPU 3.40GHz processor with RAM of 4.00 GB (3.16 usable) (8-cores). Results are taken for 1-core STLBO, 2-cores OpenMP TLBO, 4-cores OpenMP TLBO and 8-cores OpenMP TLBO on the above system by setting a task set which assigns a particular CPU cores to process or programs. To take the results of OpenMP TLBO on 16-cores and 32-cores, 8 socket Quad Core AMD Opteron™ Processor (Model 8378, 2.4 GHz, 75W ACP), RAM 24 GB is used.

In the experimentation, values of Pn and Dn are taken very large i.e. Pn = 1000 and Dn = 5000, and OSF is taken as a criterion for terminating the execution of the algorithm. In case of OSF, an algorithm is considered to be successful if the difference between the optimum solution found by the algorithm and the global optimum value is less than 0.001.

• A.    Convergence of Proposed OpenMP TLBO Algorithms

  Programming parallelization of algorithm ensure that the solution achieved should be similar in quality in compassion serial implementation. Table 2 demonstrates the ability of the proposed algorithm to find the optimal solution on 2, 4, 8, 16 and 32 cores. Population size and dimensions are set to 1000 and 200 respectively. OpenMP TLBO algorithm converges early and produces the same and better OSF than STLBO algorithm.

Table 2. Optimum Solution Found (OSF) on OpenMP TLBO algorithm

Function	STLBO	OSF in OpenMP TLBO Cores
	OSF	2	4	8	16	32
F1	0.0008	0.0007	0.0008	0.0008	0.0008	0.0008
F2	0.0008	0.0008	0.0009	0.0008	0.0008	0.0007
F3	0.0006	0.0006	0.0005	0.0006	0.0005	0.0004
F4	0.0008	0.0007	0.0008	0.0008	0.0008	0.0008
F5	0.0008	0.0007	0.0007	0.0008	0.0008	0.0008
F6	0.0008	0.0007	0.0008	0.0008	0.0007	0.0009
F7	0.0008	0.0008	0.0007	0.0008	0.0008	0.0009
F8	0.0009	0.0008	0.0008	0.0008	0.0009	0.0008
F9	0.0009	0.0009	0.0009	0.0009	0.0009	0.0009
F10	0.0008	0.0008	0.0009	0.0008	0.0008	0.0008

• B.    Effect of Number of Cores

Execution times of OpenMP TLBO on 2 to 32 cores demonstrate the speedup achieved. The speedup value is calculated by dividing the overall computational time of sequential implementation STLBO by the time taken by the parallel implementation of STLBO (i.e. OpenMP

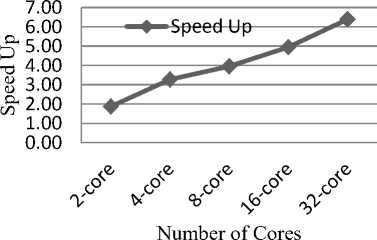
TLBO). It is seen that, as the number of cores increases, speedup increases. The results of speedup are shown in table 3A and table 3B on 2 to 32 cores. Fig. 3 shows speedup achieved for an average of all functions (F1 to F10) on 2 to 32 cores.

Table 3A. Speed ups obtained by OpenMP TLBO algorithm on 2, 4, and 8 cores system

Function	STLBO	OpenMP TLBO on 2-cores		OpenMP TLBO on 4-cores		OpenMP TLBO on 8-cores
	Time	Time	Speedup	Time	Speedup	Time	Speedup
F1	20.0599	12.25039	1.637490725	6.80687	2.947007949	6.388372	3.14006448
F2	28.76988	15.71026	1.831279686	9.38783	3.064593202	8.916324	3.226652598
F3	11.317109	5.625516	2.011745945	3.288464	3.441457471	1.957506	5.78139173
F4	61.56627	29.45228	2.090373648	16.5931	3.710353701	15.70955	3.9190346
F5	30.47906	16.24502	1.876209448	9.305884	3.27524607	8.906804	3.421997385
F6	29.30387	15.63251	1.874546698	9.050192	3.237927991	9.121547	3.212598696
F7	19.76654	10.8366	1.82405367	6.653588	2.970809133	5.648631	3.499350551
F8	49.36975	26.42954	1.867976136	14.81388	3.332668416	11.52902	4.282215661
F9	48.05734	25.6792	1.871450045	14.3507	3.348780199	10.58446	4.540367671
F10	53.6774	29.20771	1.837781873	15.82984	3.390899719	11.83986	4.533617796

Table 3B. Speed ups obtained by OpenMP TLBO algorithm on 16 and 32 cores system

Function	OpenMP TLBO on 16-cores		OpenMP TLBO on 32-cores
	Time	Speedup	Time	Speedup
F1	5.077111	3.951046176	4.406814	4.55201876
F2	6.983889	4.119464098	6.178805	4.656220742
F3	1.619893	6.986331196	1.392834	8.125238901
F4	13.5134	4.55594225	11.22061	5.486891533
F5	7.308339	4.170449674	5.678492	5.367456712
F6	6.979426	4.19860745	5.337963	5.489710213
F7	4.948327	3.994590495	3.862162	5.117998675
F8	8.550941	5.773604332	6.048994	8.161646383
F9	8.618475	5.576083936	6.007755	7.999217678
F10	8.781576	6.112501902	6.028889	8.903365114

C. Optimum Utilization of Computing Resource

Fig. 4 shows the utilization of multi-core system by STLBO algorithm. Fig. 5 shows the utilization of multicore system by OpenMP TLBO. These results show the significant speedup, optimum utilization of multi-core systems.

Fig. 3. Speedup versus number of cores

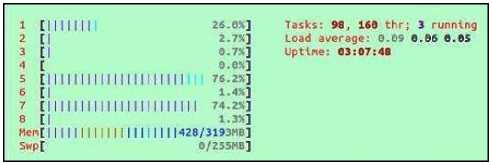
Fig. 4. Utilization of multi-core (8-cores) system by STLBO algorithm

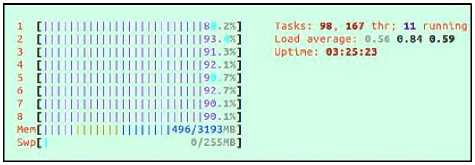
Fig. 5. Utilization of multi-core (8-cores) system by OpenMP TLBO algorithm

• D. Effect of Problem and EA Parameters

Apply parallel implementation (OpenMP TLBO) to all the test problems shown in Table 1 for studying the effect of the following properties on the speedup of the algorithm:

• 1)    Number of design variables

• 2)    Population size

• 3)    Problem complexity

  This experimentation is taken on Intel Core i7-2600 CPU (8-cores CPU system). Each run is terminated after the OSF and normalized over 10 runs.

Table 4 show the results experimentation for speedup and CPU utilization on 8-core system for dimension 200. It shows that minimum speedup is 2.97 and maximum speedup is 4.67. CPU utilization increases up to 93% using OpenMP TLBO algorithm as compare to STLBO. Table 5 show the results experimentation for speedup and CPU utilization on 8-core system for dimension 2000. It shows that minimum speedup is 3.38 and maximum speedup is 5.21. CPU utilization increases up to 93% using OpenMP TLBO algorithm as compare to STLBO.

Table 4. Performance of STLBO and OpenMP TLBO on 8-cores system for Pn=1000 and Dn=200.

Type	STLBO Time	OpenMP TLBO Time	Speedup	Efficiency	STLBO CPU Utilization	OpenMP TLBO CPU Utilization
F1	0.5943917	0.1999474	2.972740331	37.15925413	22.11	89.88
F2	0.7966197	0.2425574	3.284252305	41.05315381	23.01	92.11
F3	0.10658835	0.03465242	3.07592803	38.44910038	25.1	92.33
F4	1.744723	0.5422093	3.217803531	40.22254414	24.31	92.31
F5	0.855884	0.2612472	3.276146118	40.95182647	23.74	90.11
F6	0.7974406	0.2474692	3.22238323	40.27979037	26.54	93.21
F7	0.586408	0.1817133	3.227105556	40.33881945	23.54	93.24
F8	1.870083	0.4234461	4.416342481	55.20428102	28.47	90.12
F9	1.872172	0.4246587	4.408650994	55.10813743	24.56	90.21
F10	1.937671	0.414895	4.670268381	58.37835476	24.65	90.12

Table 5. Performance of STLBO and OpenMP TLBO on 8-cores system for Pn=1000 and Dn=2000.

Type	TLBO Time	OpenMP TLBO Time	Speedup	Efficiency	TLBO CPU Utilization	OpenMP TLBO CPU Utilization
F1	7.389233	2.182785	3.385231711	42.31539639	21.32	89.98
F2	10.71307	3.246257	3.300129965	41.25162456	29.54	91.24
F3	2.911842	0.5580366	5.218012582	65.22515727	24.51	89.62
F4	19.90186	6.123099	3.25029205	40.62865062	23.54	93.24
F5	11.27272	3.225995	3.494338956	43.67923695	24.56	90.21
F6	10.695324	3.287837	3.252997031	40.66246289	23.66	91.27
F7	7.442053	2.217287	3.356377862	41.95472327	28.87	92.22
F8	19.44875	4.591783	4.235555121	52.94443901	26.44	92.22
F9	19.07972	4.297528	4.439696495	55.49620619	20.12	90.11
F10	21.24441	4.552396	4.666643675	58.33304594	22.11	89.88

Results clearly indicate that for larger population size and design variables size, the use of OpenMP implementations of existing STLBO on a multi-core platform is beneficial.

Efficiency of the proposed algorithm is calculated using (1).

Efficiency = (Speedup / Number of cores)*100    (1)

• VI. Conclusion

This paper experimented the programming parallel TLBO(OpenMP TLBO) on multi-core system for unconstrained optimization.

OpenMP TLBO is successful in utilizing all the cores of multicore system than the STLBO. For all function the OpenMP TLBO gives remarkable speedup over STLBO.

The maximum utilization of multicore system helps OpenMP TLBO to converge early.

Results show that, the OpenMP TLBO gives linear speedup and optimizes the CPU utilization against the sequential implementation of TLBO (STLBO).

In future scope, researchers can experiment the proposed OpenMP TLBO on CEC 2013 function bed. Further constrained optimization test bed could be also experimented.

Acknowledgement

The authors are thankful to the anonymous reviewers as well as the editors for their valuable comments and suggestions which have led to improve the quality of the paper. Our special thanks to Dr. R. V. Rao for their work on Teaching Learning Based Optimization Algorithm published in various journals and conferences.