Операторное описание параксиальных световых полей

В [1] описана алгебра операторов симметрии уравнения Шредингера. В данной работе, пользуясь связью уравнения Шредингера с уравнением параксиального распространения светового поля, рассмотрена оптическая интерпретация операторов-инвариантов. Показано, что действие оператора эволюции светового поля в свободном пространстве эквивалентно преобразованию Френеля, а действие оператора эволюции в среде с параболическим показателем преломления также эквивалентно некоторому интегральному преобразованию, аналогичному преобразованию Френеля.

В [2] предложен метод формирования мод Гаусса-Эрмита (ГЭ) с помощью фазовых ДОЭ, функция пропускания которых равна знаковой функции от многочлена Эрмита заданного порядка. Такой ДОЭ должен освещаться плоской волной, ограниченной диафрагмой определенного размера.

Очевидно, что фазовый ДОЭ с конечной апертурой не может идеально точно сформировать амплитудно-фазовое распределение, описывающее моду ГЭ. Ниже с помощью численного моделирования для одномерного случая показано, что в рамках данного метода [2] можно формировать моды ГЭ с номерами от 1 до 5, отличающиеся от идеальных мод, в среднем, на 10-18%. Причем после пространственной фильтрации этих мод в Фурье-плоскости в плоскости изображения ДОЭ также формируются моды ГЭ, отличающиеся от идеальных, в среднем, уже на 5-12%. При этом энергетическая эффективность любой моды - не ниже 78% (для одномерного случая).

Также приведены результаты эксперимента по формированию двухмодового инвариантного пучка ГЭ с помощью бинарного ДОЭ, рассчитанного методом частичного кодирования [3]. Среднеквадратичная ошибка поперечного распределения интенсивности в фокальной плоскости от предсказанного теоретически составила около 12%.

базис алгебры симметрии которого(алгебра Ли) имеет 9 операторов [1]:

K =-

2 a z 8

2 к д z

K ₂ = 2 к —,

²       d z

B x =

z 8

z

2 к

д x — + 8x

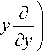
z

--+ г

2 к

P y =F, 8 y

2     2

x ² + y ²

-

P x =— , 8 x

ix

---+--, 2 к d x 2

B y =

z 8    iy

--+ —, 2 к 8 y  2

8     8         8     8      8

M = x —-y — , D = x — + y — + 2 z — + 1, E = i .

d y     8 x         8 x     8 y      8 z

Операторы (2) имеют следующие коммутационные соотношения:

[ D,K _{± 2} ] =± 2K ± 2 , [ D,B _x ,y ] = B _x ,y ,

[ D,P x,y ] =- P x,y , [ D,M ] = 0, [ M,K ± 2 ] = 0,

[ P x ,M ] = P y , [ P y ,M ] =- P x , [ B x ,M ] = B y , [ B y ,M ] =- B x , [ K 2 ,K - 2 ] = D ,                         ⁽³⁾

^K2 ,B x,y ^]= ⁰ , ^K - 2 ,B x,y ] =^{- P}x,y ,

K - 2 ,P x,y ] = 0, [ P x,y ,K 2 ] = B x,y ,

^[ B x,y^,Px,y ^]= |, ^{[ P}x,y ,B y , x , ] = 0,

где [ a,b ] = AB - BA .

Операторы симметрии L в уравнении (2) и любая их линейная комбинация переводят одно решение уравнения (1) в другое решение и удовлетворяют условию:

[L, Q]= R ( x ) Q ,

_ „ , 9   9 ²     9 ²

где Q = 2гк — +--— +--— - оператор Шредингера, dz 9x 2 9y L

R ( x ) - функция, которая может зависеть и от L .

Уравнение (1) можно представить в виде

2гк — = гк 2e , dz       2

1. Операторы-инварианты

Параксиальное уравнение распространения

(    9   9 ²    5² )

I 2 гк ^ + ^ + ^1 E ( x , y , z ) = 0,          (1)

(   dz 9x2 9y2 J где к - волновое число света, z - координата вдоль оси распространения света, можно записать в операторной форме:

где K - 2

_ 9 ■

= 2 к— = г

9 z

9 ²     9 ²

_V9 x ^{2 +}d y ²,

, решение которого

в операторной форме имеет вид:

E ( x , y , z ) = exp |     K -2 | E o( x , y ),

V 2 к       )

где E 0 ( x,y ) - функция E ( x,y,z ) при z =0.

Q E =0,

Оператор exp l — K _— 2 I - оператор, описы- X 2 k )

вающий распространение светового поля вдоль оси z . Поэтому операторы симметрии из уравнения (2), которые коммутируют с оператором К₂ , будут также коммутировать с оператором (6):

Базис операторов симметрии уравнения (1) при z =0 имеет вид:

2.2

К (0) = ix^ , Б_х (0) = j , B y (0) = 2 ,

l z exp —К 2

X 2 k "2

r f z I n К 2 n =Х 2 k ) n !

D(0) = x   + y +1, dx   dy

К — 2

. f а ²     а ² 1

Xd x ² 5 y ² )

_    5         5           5     5        .

P _x = —, P _y = —, M = x--y —, E = i .

5 x    ^y 5 y        5 y   5 x

то есть являются инвариантами распространения.

Можно показать, что действие оператора распространения (6) эквивалентно преобразованию Френеля:

Операторы (10) подчиняются тем же коммутационным соотношениям (3). Операторы (2) и (10) связаны между собой формулами:

f I            “f i, I n

exp| 4vK"2 IE0(x,У)= rkrl (n!) jjEofcn)

2 k                   2 k n —0^           —”

L ( z ) = exp l — К _ 2 I L (0) exp l — — К — 2 X 2 k ) X 2 k

n a2 a2 i                              ” f i? In

,-+ТГ I a(x—^У — nWn =Ekr| (n!)

d x ² d y ² )                        n = 0 X 2 k )

jj F(а, в)(a2 + в2) exp[— i(xa + yP^аРв =

-”

Оптический смысл оператора К₂ ( z ) в том, что он описывает изменение эффективного радиуса светового поля, определенного как момент второго порядка по интенсивности при распространении вдоль оси z . Действительно,

= “j F (a, в )exp

-”

x exp[— i (xa + yP)] dadp =

= ^Tk" 11Eo (§- П)exp(i k- [(x — ^)2 + (y — n)2 I d^dn 2nz —“             t 2z                   JJ

—

z

i

2 k

x

”

jj E0 (x, y)K 2 E0 (x, y) dxdy =

—”

”

= j j E * (x, y, z)K2 (0) E (x, y, z) dxdy = —”

где < X x,y ) - дельта-функция Дирака, F( а , в ) - Фурье-образ функции E 0 ( ^ , n ).

Из уравнения (3) видно, что имеются пять операторов-инвариантов. Операторы P_x и P y описывают малые смещения светового поля по осям x и y соответственно (операторы сноса пучка [4]). Оператор К _2 описывает дифракционную расходимость светового поля. Оператор M определяет малые повороты вокруг оси z и может быть назван оператором углового момента [5]. Оператор E определяет тождественное преобразование и связан с сохранением

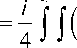
x ² + y ²) | E ( x , y , z ) |² dxdy =

2 k

2k

i

+—

”

j j E0* (x, y )K—2 E0 (x, y) dxdy —

—”

”

jje0

—”

(x, y )D (0) E0 (x, y) dxdy +

”

jj(x2 + y2)|E0 (x,y) |2 dxdy

—”

энергии светового поля при его распространении. Из этих пяти операторов-инвариантов с помощью линейных комбинаций можно образовать и другие

Независящие от z интегралы в уравнения (12):

инвариантные операторы.

Остальные четыре оператора из (3) не являют-

”

j j ^E 0 ^{( x} , y ^{) К} — 2 ^E 0 ^{( x} , y ^)d x d y ,

—”

ся инвариантами распространения, но тоже имеют наглядный физический смысл. Операторы Б_х и B y при z =0 описывают малый наклон светового поля вдоль оси x и y соответственно. Оператор К₂ при z =0 описывает малую квадратичную фазовую задержку светового поля. Оператор D при z =0 описывает малые растяжения (сжатия) светового поля по осям x и y .

Можно показать, что действия перечисленных операторов определяются следующими формулами:

”

j j ^E 0 ⁽ x , y ^{) D (0) E} 0 ⁽ x , y ^)d x ^d y

—”

exp ( 0 M ) E 0 ( r , ф ) = E 0 ( r , ф + 0 ),

описывают расходимость светового поля из-за дифракции и смещение с оптической оси, соответственно .

Алгебра операторов (2), (3) описывает не только распространение светового поля в свободном пространстве, но также распространение его в волноводе с параболической зависимостью показателя преломления:

exp [ c D (0) ] E ₀ ( x , y ) = e c E ₀ ( e c x , e c y

^ex p [ 6 ^К2 ^{(0) ]} E 0⁽ x , y ) = exp l

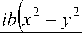
idx

T

j

^E 0 ⁽ x , y )>

n ^{2 (} r ) = n 2

f ,.2 I

1—2A

X

r0 )

^ex p ^{[ d} B x ^{(0) ] E} 0⁽ x , y ) = exp l

^E 0 ^{( x} , y )

exp [ a P x ] E 0 ( x , y ) = E 0 ( x + a , y ).

где n₀ - показатель преломления на оси, А - параметр дисперсии показателя преломления, r 0 - радиус волокна.

Параксиальное уравнение, описывающее световое поле в среде (13) имеет вид:

(

к

d d ² d ²

2 ik T+  7+  7-a dz 8x 2 dy

2    2 k

2 X ² + y ²

■ E ( x , y , z ) = 0, (14) J

Действие операторов симметрии exp( a L ) на решение уравнения (1) E ( x,y,z ) эквивалентно действию операторов T , определенных матрицами A :

где a = 2V2A —.

r ₀

В операторном виде уравнения (14) можно записать

T ⁽| A |)= ^exp ^{( a L} )

, aS -py =1.

2 ik— = i L₃₆ E ,                          (15)

8z где L36 = K-2 - a2K2 (0).

Замкнутая алгебра операторов L_{3 a} , D (0) и

L _{2 б} = K _{- 2} + a ² K 2 (0) имеет вид:

Действие оператора T описывается соотношением:

I a в 1 z

Tl     ;I E (x, y, z) = к Y S J

[ L 3 a , D ( 0 )] = 2 L 2 a , [ L 2 a , D ( 0 )] = 2 L 3 a , [ L 2 a , L 3 a ] = 2 a 2 D ( 0 )

exp

I" ^{i e} ( x ² + y ² )

4 u

u

_ I x y у + az /2 k

- E l —,—,---------- к u u u

,

Решение уравнения (15) можно записать в опе-

раторном виде

E ^{( x} , y , ^z ) = exp l     L₃₆ I E 0 ^{( x} , y ) .

к 2 k      J

^z где u = о + — в . 2 k

Для конкретных операторов уравнения связи (21) имеют вид:

Можно показать, что для оператора распространения в среде с параболическим показателем преломления (13) имеет место соотношение:

exp⁽ a K - 2 ) = T Г¹ 0 |, exp⁽ b D ⁽0⁾⁾= T I e 0 |, к a 1J                     к 0 e ^b J

exp⁽    L 36 ) = exp ⁽ a ^K 2 ^{(0) ) e}xp ⁽ b ^K - 2 ^{) e}xp ⁽ c ^{D (0) ) ,(18)}

2 k

exp ( c L 3 ) = T I c^Os( c )) к sin( c )

- sin( c ) cos( c )

_z . ,   sin( ^ z )

a = -a tg( ^ z ), b = —-----,

2a где                                . (19)

c = ln [ cos( ® z )], ю = —

Из (18) с учетом (8) и (9) следует:

exp|    L36 |E0 (x, у) = ,a,    . x к 2k J           4n i sin(m z)

I 1 ^exp ( d K 2 ⁽0) ) = ^T I 0

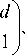
где L 3 = K _2 - K 2 .

Формулы (23) дают связь операторного и матричного описаний светового поля.

^x exp

i a ctg(m z )/ 2    2 j

4 к ^{+ y} )

x

x 7 ( e₀ (^, n)expj--- ^{i a}---x

J _m^J 0           [ ⁴sln(m z )

x [( ^ ² +n 2 ) cos(m z ) - 2( x ^ + y n) ]} d ^ d П

Уравнения (20) является аналогом преобразования Френеля (8) в среде (13). Из уравнения (20) видно, что при z m =( п /2+ т п ) ю^х в среде будет формироваться Фурье-спектр исходного поля, а при z m = т пю^х будет формироваться изображение исход-

2. Формирование инвариантных пучков

Примером решения уравнения (1) могут служить моды Гаусса-Эрмита и Гаусса-Лагерра [6]. Они инвариантны к действию оператора распространения в свободном пространстве с точностью до масштаба.

В работах [2, 7] предложен простой метод расчета фазовых ДОЭ для эффективного формирования одномодовых гауссовых пучков, основанный на пропорциональности функции пропускания ДОЭ знаковой функции соответствующего полинома. Например, для мод Гаусса-Эрмита:

^exp\i V nm ^{( x} , y ^{) ]} =

ного поля.

Заметим, что так как оператор углового момента M коммутирует с операторами K -2 (0), K 2 , D (0), то из уравнения (18) следует, что оператор M также коммутирует с оператором распространения в среде с параболическим показателем преломления

I z             । expl —L36 I. Поэтому можно утверждать, что уг-к 2 k    J ловой момент светового поля при распространении в такой среде сохраняется.

= exp < i arg H_n

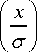
+ i arg H m

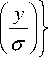
где H_n ( x ) - полином Эрмита, с - параметр, характеризующий эффективную ширину моды ГЭ.

При освещении фазового ДОЭ (24) плоской или гауссовой волной в спектральной плоскости сформируется световое поле с комплексной амплитудой, близкой к заданной моде. Сохранение структуры формируемого пучка на различных расстояниях подтверждает его модовый характер [8].

Введение в спектральную плоскость диафрагмы, аналогично [9], позволяет получать в плоскости изображения световое поле, также близкое к заданной моде. На рис. 1 показана оптическая схема для формирования гауссовых мод.

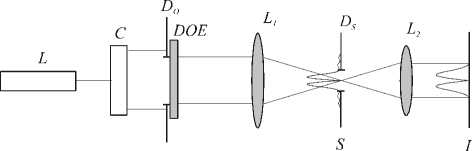
Рис. 1. Оптическая схема для формирования гауссовых мод.

Гелий-неоновый лазер L освещает DOE , фаза которого пропорциональна знаковой функции соответствующего полинома. Диафрагма D O подстраивается на оптимальный для формируемой моды размер [10]. Сферическая линза L₁ формирует в плоскости S пространственный спектр, из которого диафрагмой D S выделяется эффективная часть. Полученное с помощью сферической линзы L 2 в плоскости I изображение имеет комплексную амплитуду, демонстрирующую модовый характер сформированного поля.

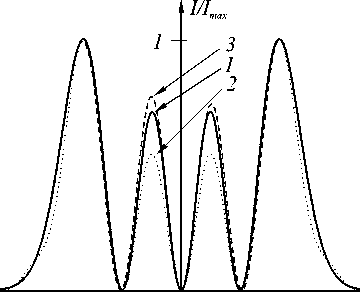
На рис. 2 и 3 показано формирование 4-й и 5-й мод ГЭ соответственно. При этом для наглядности все распределения амплитуды и интенсивности выравнены по максимальному значению, а не по энергетическим характеристикам. На рис. 2а и 3а показано распределение амплитуды идеальной моды (линия 1) и бинарная фаза ДОЭ (линия 2). На рис. 2б и 3б показано распределение интенсивности, получаемое в спектральной плоскости при освещении ДОЭ плоским пучком (линия 2) и для сравнения распределение интенсивности идеальной моды (линия 1). Положение диафрагмы здесь выделено пунктирной линией. На рис. 2в и 3в показаны распределения интенсивности в плоскости изображения (линия 3), Фурье-образа такого изображения (линия 2) и идеальной моды (линия 1). На рис. 2г и 3г приведены соответствующие фазы.

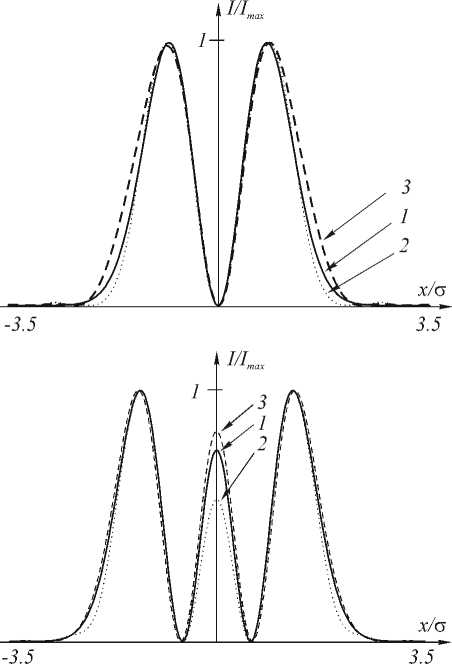
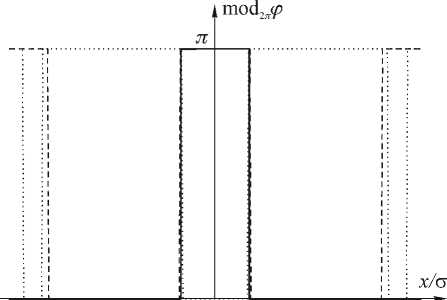
На рис. 4 приведены аналогичные результаты для 1-й, 2-й и 3-й мод ГЭ. На рис. 4а, в, д показаны распределения интенсивности в плоскости изображения (линия 3), Фурье-образа такого изображения (линия 2) и идеальной моды (линия 1). На рис. 4б, г, е приведены соответствующие фазы.

I

A/A max

i 1

x/ σ

-7.5

-3.42                 3.42

-3.42  М 3.42

7.5

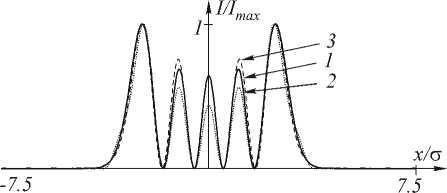
Рис. 2. Формирование 4-ой моды ГЭ с помощью бинарного фазового ДОЭ.

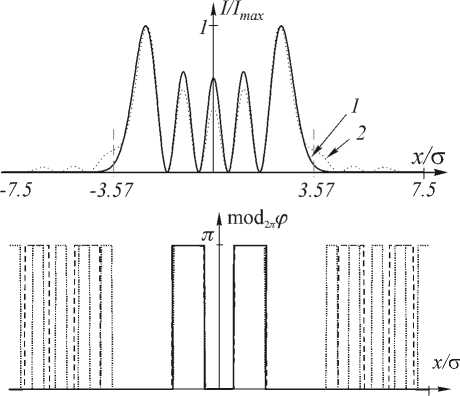
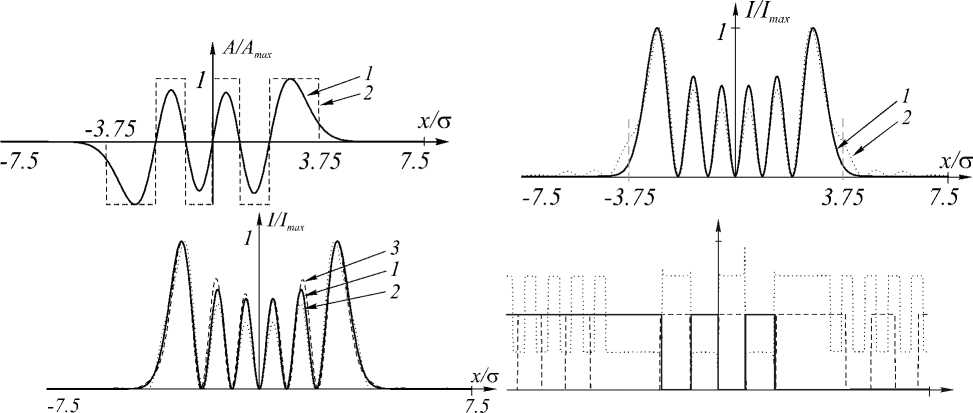
Рис. 3. Формирование 5-ой моды ГЭ с помощью бинарного фазового ДОЭ.

mod 2π ϕ 2π

π

' x/ σ

3.5

-3.5

-3.5

3.5

mod 2π ϕ

x/ σ

-3.5                                                3.5

-3.5

2π

π

I x/ σ

3.5

Рис. 4. Формирование 1-ой (а, б), 2-ой (в, г) и 3-ей (д, е) мод ГЭ с помощью бинарных фазовых ДОЭ.

Из рисунков 2в, г, 3в, г и 4 видно, что сформированные световые поля имеют модовый характер, то есть сохраняется как амплитудное, так и фазовое распределение в плоскости изображения и спектральной плоскости. При сравнении фазовых распределений нужно учитывать, что после каждого преобразования Фурье моды ГЭ приобретают фазовый набег π n /2, где n - номер моды. В таблице 1 приведены фазовый набег (взятый по модулю 2 π ) в плоскости изображения - ϕ _I и фазовый набег в следующей спектральной плоскости - ϕ SS . Понятно, что для мод ГЭ, номер которых n кратен 4, фазовый портрет будет одинаковым как в плоскости изображения, так и в спектральной плоскости. Для четных мод ГЭ, но не кратных 4, комплексные распределения в плоскости изображения и в спектральной плоскости будут находиться в противофазе.

На рис. 5. показаны графики среднеквадратичного отклонения распределения интенсивности от идеальной в спектральной плоскости δ S для 4-й (линия 1) и 5-й (линия 2) мод ГЭ, а также в плоскости изображения δ I для 4-й (линия 3) и 5-й (линия 4) мод в зависимости от размера диафрагмы. Интересно отметить, что если глобальные минимумы на рис. 5 (линии 1, 2) соответствуют оптимальному размеру ДОЭ, то дополнительные (локальные) минимумы совпадают с последними нулями полиномов Эрмита.

Оптимальные размеры ДОЭ x0/σ и диафрагмы в спектральной плоскости xS/σ приведены в сводной таблице 1. Из таблицы видно, что среднеквадратичное отклонение распределения интенсивности в плоскости изображения от идеального δI, как правило, меньше отклонения в спектральной плоскости δS. При этом отклонение в следующей спектральной плоскости 5SS (то есть для Фурье-образа изображения) меньше, чем SS. То есть оптическая система на рис. 1, повторяемая последовательно несколько раз, представляет собой некоторое приближение резонатора.

На рис. 6 приведены графики энергетической эффективности е (линии 1, 2) и среднеквадратичное отклонение распределения интенсивности от идеального (линии 3, 4) в зависимости от количества преобразований Фурье, к , для 4-й (линии 1, 3) и 5-й (линии 2, 4) мод ГЭ. При этом к =0 соответствует плоскость ДОЭ, к=1 - первая спектральная плоскость (см. 5 $ , e _S в Таблице 1), к=2 - первая плоскость изображения (см. 5 I , e I в таблице 1), к =3 - вторая спектральная плоскость (см. 5 SS в таблице 1), к =4 - вторая плоскость изображения.

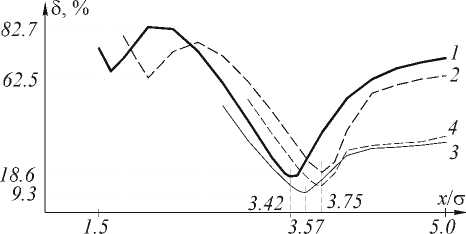
Рис. 5. График среднеквадратичного отклонения распределения интенсивности от идеального в спектральной плоскости 5 _S для 4-й (линия 1) и 5-й (линия 2) мод ГЭ в зависимости от размера ДОЭ x 0 □ , а также в плоскости изображения 5 _I для 4-й (линия 3) и 5-й (линия 4) мод в зависимости от размера диафрагмы x _S / c .

Из рис. 6 видно, что после этапа низкочастотной фильтрации в первой спектральной плоскости ( к =1) дальнейшие потери энергии незначительны. То есть практически вся энергия изображения, как и спектра, сосредоточена на конечном интервале, что также свойственно гауссовым модам.

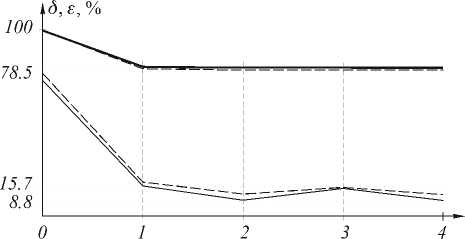
Рис. 6. Графики энергетической эффективности ε (линии 1, 2) и среднеквадратичное отклонение распределения интенсивности от идеального (линии 3, 4) в зависимости от количества преобразований

Фурье, k , для 4-й (линии 1, 3) и 5-й (линии 2, 4) мод ГЭ.

• 3.    Эксперимент

В работе [8] была экспериментально продемонстрирована возможность эффективного (65-70%) формирования одномодовых пучков ГЭ с невысокими индексами - (1,0), (1,1), (1,2) - бинарными ДОЭ с фазой (24). Однако точность формируемых мод сильно зависит от размера освещающего пучка или диафрагмы, которая его ограничивает.

В [3] был предложен метод частичного кодирования, позволяющий варьировать соотношение двух параметров - точности и энергетической эффективности - в широком диапазоне.

На рис. 7. показаны результаты эксперимента по формированию инвариантного двухмодового пучка ГЭ (0,5)+(5,0) бинарным фазовым ДОЭ с уровнем кодирования 0,5. В этом случае теоретическое среднеквадратичное отклонение от идеального распределения интенсивности в фокальной плоскости составляет около 9% при энергетической эффективности 20%.

Таблица 1.

n	x 0 / σ	δ S , %	ε S , %	x S / σ	δ I , %	ε I , %	δ SS , %	ϕ I	ϕ SS
1	2,25	10,09	85,59	3,50	12,00	85,45	6,09	П	3 П 2
2	2,70	14,91	83,33	3,32	7,98	83,22	12,47	0	П
3	3,10	15,51	81,76	3,42	6,67	81,49	13,82	П	п /2
4	3,42	16,70	80,50	3,57	9,32	80,03	15,20	0	0
5	3,75	18,60	79,45	3,75	12,48	78,71	15,92	П	З п /2

(а)

(б)

(в)

(г)

(д)

(е)

(ж)

(з)

Рис. 7. Эксперимент по формированию инвариантного двухмодового пучка ГЭ (0,5)+(5,0): бинарная фаза ДОЭ (а), теоретическое распределение интенсивности в фокальной плоскости (б), экспериментально зафиксированное поперечное распределение интенсивности на расстояниях z =900 мм (в), z =975 мм (г), z =1075 мм (д), z =1125 мм (е), z =1225 мм (ж), z =1350мм (з) от плоскости ДОЭ при освещении его сходящимся пучком.

Бинарный ДОЭ с фазой, показанной на рис. 7а, был изготовлен в Университете Йоенсуу (Финляндия): диаметр - 10 мм, 2000 x 2000 отсчетов размером 5 x 5 мкм. Результаты эксперимента, зафиксированные телекамерой с разрешением 8,59 x 8,43 мкм, при освещении ДОЭ сходящимся пучком показаны на рис. 7: поперечное распределение интенсивности на расстояниях z =900 мм (рис. 7в), z =975 мм (рис. 7г), z =1075 мм (рис. 7д), z =1125 мм (рис. 7е), z =1225 мм (рис. 7ж), z =1350 мм (рис. 7з) от плоскости ДОЭ. Видно, что сформированное поле демонстрирует инвариантные (с точностью до масштаба) к распространению свойства. Заметны некоторые вариации в центральной части картины там, где амплитуда не была закодирована.

Нужно отметить хорошую согласованность теоретических и экспериментальных результатов: среднеквадратичное отклонение распределения интенсивности на различных расстояниях от теоретически рассчитанного в фокальной плоскости (рис. 7б) составило следующие величины: 17,4% (z=900 мм), 15,2% (z=975 мм), 11,7% (z =1075 мм), 12,3% (z =1125 мм), 15,7% (z =1225 мм), 16,8% (z =1350 мм). Минимальная ошибка (около 12%), как и следовало ожидать, наблюдалась на расстоянии z =1075 мм (рис. 7д), что соответствует фокаль- ной плоскости сходящегося освещающего пучка. При этом отклонение после прохождения фокальной плоскости меньше, чем отклонение до нее. Этот эффект связан с чисто фазовым характером ДОЭ: для того, чтобы фазовое распределение под воздействием дифракции перешло в амплитудное, необходимо, чтобы световая волна преодолела определенное расстояние.

Заключение

В данной работе дана оптическая интерпретация операторов симметрии алгебры Ли параксиального уравнения распространения. Показано, что действие оператора эволюции светового поля в пространстве и в параболической среде эквивалентно интегральному преобразованию, аналогичному преобразованию Френеля.

С помощью компьютерного моделирования показано, что фазовый ДОЭ, функция пропускания которого равна знаковой функции от многочлена Эрмита n -го порядка, освещаемый плоской волной, ограниченной диафрагмой определенного размера, формирует моду ГЭ с номером 1-5, отличную от идеальной не более чем на 13%.

Приведены результаты эксперимента по формированию двухмодового инвариантного пучка ГЭ. Отличие экспериментальных результатов от теоретических составило 12%.

Работа поддержана Российским фондом фундаментальных исследований (гранты 98-01-00894, 99-01-39012, 00-15-96114, 00-01-00031).