Описание деформационных свойств материалов при расчетах малоцикловой усталости

Долговечность конструкций при малоцикловом нагружении лимитируется либо образованием трещин, либо накоплением недопустимых перемещений, т. е. изменением геометрии конструкции, делающим невозможным ее дальнейшее использование. Первое из этих предельных состояний, т. е. образование трещин, встречается чаще, и его исследованию посвящено большое число работ - [1-6 и др.]. Методы экспериментальных исследований стандартизованы [7-9], а их результаты представляются в виде кривых усталости [10–12] или законов суммирования циклических и статических повреждений [3, 13].

Неупругое деформирование конструкций сопровождается перераспределением напряжений, и определение размахов деформаций в опасной точке конструкции требует учета деформационных свойств материала (в отличие от испытаний образцов на малоцикловую усталость в условиях однородного напряженно-деформированного состояния). Современные пакеты МКЭ сняли вопрос учета реальной геометрии детали, но вопрос описания свойств материала нельзя считать окончательно решенным. За пределами упругости эти свойства зависят не только от технологии изготовления, но и от всей предшествующей истории неупругого деформирования. Конкретные проявления этой зависимости весьма разнообразны. Следствием явилось появление в библиотеках свойств материалов пакетов МКЭ многих десятков различных моделей деформирования [14, 15], развивающихся в направлении попыток охватить все больший круг эффектов. Чаще всего эти модели приводятся без указания конкретных границ применимости. Отсутствие общепринятого подхода с доказанной адекватностью компенсируется большими коэффициентами запаса по числу циклов (например, n N = 10 в [12]). Результатом является существенное сокращение маневренности конструкций, возможностей и скоростей изменения режимов работы при нормальной эксплуатации.

Механика

В то же время деформационных характеристик, определяемых в стандартных испытаниях на малоцикловую усталость, может оказаться достаточно для расчета в некоторых случаях. Такой подход, рассматриваемый ниже, возможен на основе дифференциации различных типов малоциклового деформирования, стадий работы конструкции и целей расчетов.

Типы и стадии малоциклового деформирования

В широко известной работе [16] были выделены 3 типа неупругого деформирования (знакопеременное течение, прогрессирующее накопление деформаций, их комбинация) и для модельной конструкции определены комбинации нагрузок, приводящих к реализации каждого типа деформирования. Решение Bree вошло в нормативные документы [10] и было распространено на другие конструкции.

Отметим некоторые особенности решения Bree. Во-первых, оно получено для идеально упруго-пластического материала со свойствами, не зависящими от типа деформирования в цикле (эксперименты – см., например, [17] – показывают, что это не так). Во-вторых, решение Bree было выполнено с использованием критерия текучести Треска – Сен-Венана, поверхность текучести которого кусочно-линейна. Такой характер поверхности текучести вместе с ассоциированным законом течения и обусловил существование области «чистого знакопеременного течения» конечного размера – рис. 1. Если векторы скорости пластической деформации в 2 момента времени цикла параллельны, то их сумма может быть равна 0 (чистое знакопеременное течение без накопления деформаций). Для критерия Мизеса параллельность этих векторов достигается лишь при идеальной симметрии цикла напряжений; цикл, смещенный постоянной нагрузкой от начала координат, сопровождается накоплением деформаций – см. рис. 1. Нужно отметить здесь разницу между силовым и кинематическим – скажем, тепловым – нагружением. При кинематическом нагружении вырабатываемые остаточные деформации приводят к симметризации цикла, а при силовом нагружении – нет. В задаче Bree, моделирующей реальную конструкцию – ТВЭЛ атомного реактора, – силовое и кинематическое нагружение сочетаются: внутренне давление соответствует силовому нагружению, а перепад температур – кинематическому. Оценивать соотношение между размахом деформаций в цикле и накоплением за цикл можно через величины соответствующих повреждений. Пример результатов конечно-элементных расчетов задачи Bree с использованием критерия текучести Мизеса и методик расчета статического и циклического повреждения из [13] приведен на рис. 2.

Задача Bree характерна тем, что в рассматриваемой конструкции – длинной цилиндрической оболочке – отсутствует перераспределение напряжений по длине и окружности; именно это обеспечивает возможность существования «чистого накопления деформаций». Для конструкций с концентраторами напряжений и локальной зоной неупругого циклического деформирования такое накопление может быть исключено – за счет упругой части конструкции. Однако это верно лишь для стабильного цикла, т. е. стадии стабильной работы конструкции. На стадиях приработ- ки и предразрушения это не так.

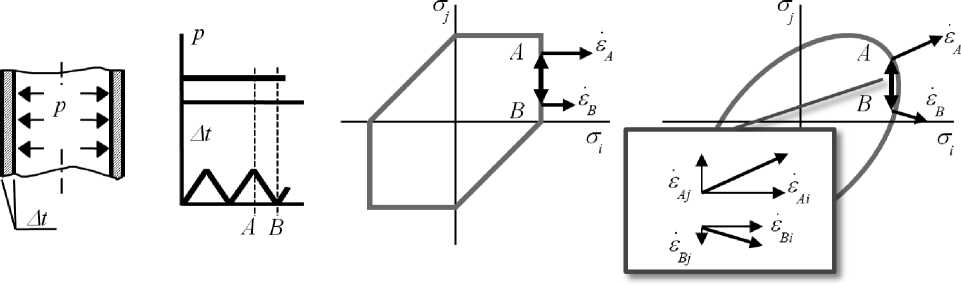
Рис. 1. Поверхности текучести Треска–Сен-Венана и Мизеса (и векторы скорости пластической деформации в разные моменты цикла)

Чернявский О.Ф., Чернявский А.О.

Описание деформационных свойств материалов при расчетах малоцикловой усталости

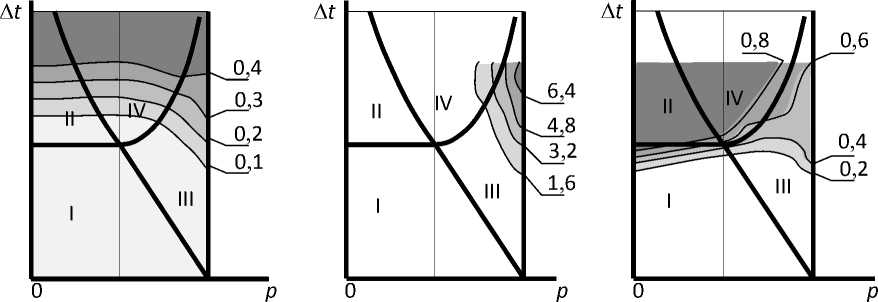
Рис. 2. Решение Bree и доли статического и циклического повреждения при использовании критерия Мизеса: а) интенсивность размахов деформации за цикл; б) интенсивность приращений деформации за цикл; в) доля циклической составляющей в суммарном повреждении за цикл

Материал в решении Bree полагается стабильным: свойства не меняются от цикла к циклу и не зависят от типа деформирования. Свойства реальных материалов от типа деформирования зависят вследствие проявления эффектов, невозможных при однократном нагружении: при знакопеременном течении - циклическое упрочнение-разупрочнение и многократное ускорение неус-тановившейся ползучести вследствие предшествующей пластической деформации другого знака; при прогрессирующем формоизменении - повторением в каждом цикле неустановившейся ползучести при высоких напряжениях (ползучесть ниже не рассматривается).

На стадии приработки от цикла к циклу меняются свойства материала (циклическое упрочнение или разупрочнение) и поля остаточных напряжений и деформаций в конструкции. Эксперименты [4, 17] показывают, что для стабилизации свойств материала обычно достаточно нескольких десятков циклов. Примерно такое же количество циклов нужно для стабилизации полей остаточных деформаций и размахов деформаций за цикл при стабильных свойствах материала. Для конструкций с плановым ресурсом порядка 10 000 циклов, например авиационных двигателей, повреждения, накапливаемые на стадии приработки, оказываются небольшими. Это является основанием для достаточно многочисленных попыток ограничиться рассмотрением накопления повреждений только в стабильных циклах, см., например [18, 19].

Однако в ряде задач такой подход не может быть использован. К ним относятся задачи расчетов конструкций с малым плановым ресурсом и расчеты на стадии предразрушения.

Особенности технологии расчетов кинетики деформирования

Для конструкций с плановым ресурсом на уровне десятков и сотен циклов стадия приработки может составлять значительную часть ресурса - особенно при наличии ползучести, вызывающей продолжающееся от цикла к циклу изменение границы зоны неупругого деформирования. Одним из вариантов анализа работы конструкции в этих условиях является расчет кинетики неупругого деформирования.

Существенное влияние на результаты расчета этой стадии работы конструкции могут оказать остаточные напряжения и изменения пределов текучести (наклепы) вследствие деформирования в технологическом процессе. В качестве примера на рис. 3 показаны поцикловые расчеты кинетики окружной деформации s t , осевой деформации s x и интенсивности деформаций s i в задаче Bree в случае отсутствия и наличия технологических остаточных напряжений. Остаточные напряжения сдвигают петлю гистерезиса, изменяя значения накопленных к моменту стабилизации компонент деформаций и размахов интенсивности деформаций (размахи компонент и, соответственно, интенсивность размахов при этом не зависят от остаточных напряжений).

Отметим, что расчетное получение информации об остаточных напряжениях и наклепах требует моделирования всего технологического процесса, является сложным и применяется редко. Одним из первых примеров, по-видимому, может считаться работа [20]. Несмотря на рост вычислительных возможностей, эти задачи, прежде всего в силу сложности получения и недостаточной надежности исходных данных, остаются скорее уникальными, чем типичными.

Механика

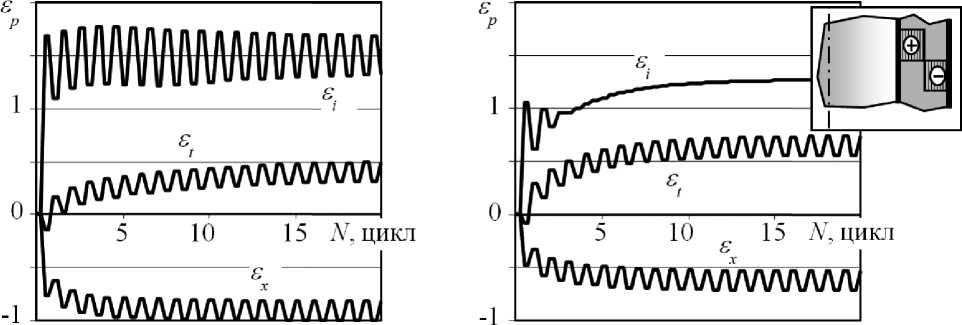
Рис. 3. Результаты поциклового расчета неупругих деформаций в задаче Bree при отсутствии или наличии технологических остаточных напряжений. Справа вверху – распределение окружных остаточных напряжений на начало процесса

Экспериментальное получение этой информации затрудняется необходимостью разрушить деталь (для определения остаточных напряжений) и высокими градиентами свойств и напряжений в приповерхностных слоях, зонах термического влияния сварных швов и т. п.

Для оценки возможности получения информации о наклепах и остаточных напряжениях неразрушающим методом была предпринята попытка моделирования определения твердости по Бринеллю в образце из стали 12Х18Н10Т. Условия моделируемых испытаний соответствовали ГОСТ 9012-59. Истинная диаграмма деформирования материала строилась по значениям предела текучести (196 МПа) и предела прочности (491 МПа) из [12] с использованием аппроксимирующих формул приложения 3.D к [11]. Попытка оказалась неудачной: предварительное растяжение до 350 МПа (и последующая разгрузка) с целью создания наклепа изменило расчетную величину вдавливания менее чем на 5 %, что, по-видимому, лежит в пределах точности измерений. Причиной является то, что предварительное растяжение поднимает наблюдаемый предел текучести лишь в направлении предварительного растяжения, а на результатах вдавливания шарика сказываются усредненные по направлениям свойства (возможно, вдавливание призмы в 2 взаимно перпендикулярных направлениях могло бы дать дополнительную информацию, но такие испытания не являются стандартизованными). Влияние остаточных напряжений на вдавливание шарика может маскировать даже это небольшое влияние наклепа, так как знаки изменений оказываются различны.

Таким образом, целью расчета на стадии приработки может быть оценка ширины петли неупругого деформирования для определения уровня циклического упрочнения (разупрочнения) материала с использованием циклической кривой – в предположении, что соответствующее упрочнение (разупрочнение) успевает полностью реализоваться. Такой расчет, по-видимому, не имеет смысла, если плановый ресурс конструкции достаточно велик и стадия стабильной работы (см. ниже) достаточно продолжительна для того, чтобы установившиеся на этой стадии размахи и уровни упрочнения слабо зависели от стадии приработки.

На стадии стабильной работы единственность решения, как известно, доказывается лишь для областей, где идет пластическое деформирование – при условии известных свойств материала. Учет циклического упрочнения-разупрочнения может быть сделан итерационным способом: путем последовательных расчетов нескольких циклов, оценки ширины петли гистерезиса и величины накопления деформаций за цикл, и подстановки соответствующих им свойств материала – с последующим повторением расчета. Такая процедура сложнее, чем применяемые сейчас (реализованные, например, в пакете ABAQUS) процедуры расчета стабильных циклов, предполагающие независимость диаграмм циклического деформирования от размахов и приращений деформаций в цикле.

Если приращения деформаций в цикле невелики и свойства материала близки к свойствам при жестком циклическом нагружении, то в расчет должны быть заложены диаграммы циклического деформирования в стабилизированном жестком цикле для каждого заданного размаха

Чернявский О.Ф., Описание деформационных свойств материалов Чернявский А.О. при расчетах малоцикловой усталости деформаций в цикле. При отсутствии таких данных в справочной литературе в качестве первого приближения можно, видимо, рекомендовать коррекцию кривой однократного деформирования на основе циклической кривой (см., например, [4]) и предположения, что модуль упругости не меняется. Технологически описать такое изменение диаграмм в существующих пакетах можно так же, как изменение диаграмм при нагреве. При этом после расчета одного цикла деформирования конструкции в каждой точке (каждом конечном элементе) должна быть вычислена интенсивность размаха неупругой деформации, по ней – величина упрочнения и выбрана соответствующая «температура», определяющая диаграмму деформирования. Повторять процесс нужно до обеспечения сходимости, понимаемой как малое отличие последовательных циклов (более корректным является сравнение не 2 последовательных циклов, а результатов расчетов в текущем цикле с результатами экстраполяции по рассчитанным циклам на большое число циклов). При изотермическом нагружении такая процедура может быть реализована в конечноэлементных пакетах использованием зависимости свойств от квази-температуры; нужно только иметь в виду, что в существующих пакетах (в частности, ANSYS) нет встроенных средств расчета интенсивности размахов неупругих деформаций и соответствующей «квази-температуры», это должно быть сделано, например, с использованием программирования на встроенных языках пакетов МКЭ (APDL в ANSYS, Python в ABAQUS и т. п.).

В качестве методического примера ниже рассмотрен расчет круглого образца с кольцевой выточкой. В качестве материала рассматривается сталь 12Х18Н10Т; диаграммы деформирования, восстановленные по аппроксимационным формулам [4], показаны на рис. 4.

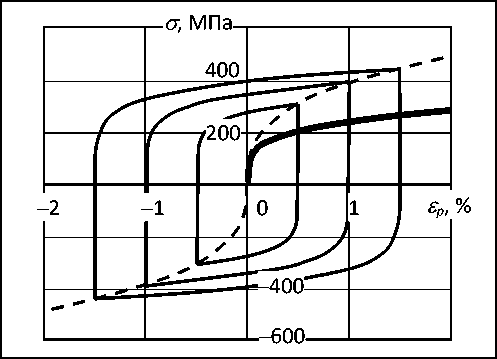
Рис. 4. Диаграмма деформирования при монотонном нагружении (жирная кривая), циклическая кривая (штриховая) и диаграммы деформирования в стабильных циклах с разными размахами деформаций

Для диаграмм циклического деформирования (в координатах ст * , s p* , отсчитываемых от точки реверса) использовано степенное описание вида с * = A s p*¹¹ с постоянным значением показателя n = 0,08 [4]; множитель A определяется из условия, что при заданной амплитуде неупругой деформации s pa вершины петель гистерезиса попадают на циклическую кривую:. При задании свойств материала в ANSYS учитывается то, что в модели материала с кинематическим упрочнением реализуется принцип Мазинга, и диаграммы циклического деформирования задаются в виде «однократных» диаграмм, центрально подобных полученным с коэффициентом подобия 1/2.

Результаты расчетов существенно зависят от методики. Так, максимальная интенсивность размаха пластических деформаций за цикл, рассчитанная при описании свойств материала кривой однократного деформирования составляет 1,54 %; при описании кривой, учитывающей упрочнение, определенное по размахам деформаций вдали от концентратора – 1,87 %; при полном учете упрочнения (упрочнение в каждой точке конструкции зависит от размаха деформаций в этой точке) – 0,81 % (см. рис.5). Учитывая, что долговечность в малоцикловой области обратно пропорциональна квадрату размаха деформаций в цикле, найденные различия представляются очень существенными с точки зрения оценки ресурса конструкции – до 5 раз.

Единственность решения обеспечивается лишь в том случае, если упрочнение зависит от размаха деформаций в стабильном цикле и не зависит от истории. В общем случае это не так – см., например, [21]. Предложенная выше технология предполагает отсутствие в программе нагружения перегрузок, которые могли бы привести к повышенному упрочнению материала.

Механика

Если нагружение является неизотермическим или если в стабильном цикле обнаруживается – кроме размаха – накопление неупругой деформации, которое меняет свойства материала [17], то замена диаграммы деформирования несколько осложняется. Возможным выходом является создание набора описаний материала, каждое из которых содержит диаграмму стабильного деформирования в определенных условиях, выбор соответствующего описания по результатам расчета и повторение этой процедуры до обеспечения сходимости. Описание зависимости упрочнения от размаха и приращения неупругой деформации в цикле при этом получается дискретным (кусочно-постоянным). В существующих пакетах «замена» материала не может быть сделана в середине программы нагружения, поскольку получающиеся поля накопленных деформаций и остаточных напряжений не будут удовлетворять условиям совместности и уравнениям равновесия. Необходима итерационная процедура обеспечения сходимости.

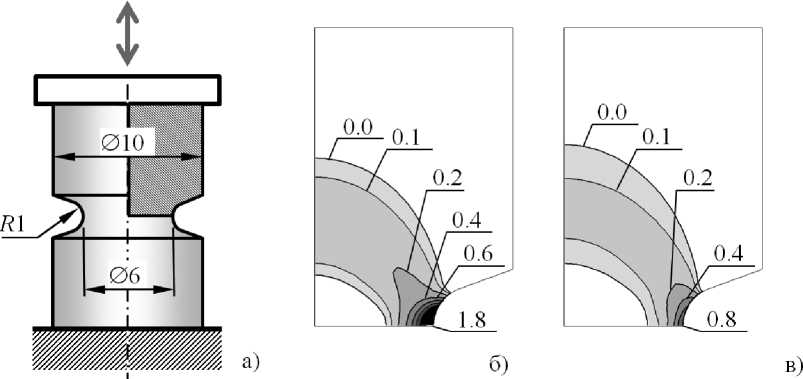
Рис. 5. Распределение интенсивности размаха пластических деформаций (в %) в круглом образце с надрезом при жестком циклическом нагружении: а) схема, б) расчет без учета циклического упрочнения, в) с учетом (разный уровень упрочнения в разных точках конструкции)

Наиболее трудной проблемой является расчет на стадии предразрушения и разрушения. Циклическое разупрочнение, характерное для материала на этой стадии, не позволяет считать стабильный цикл и вынуждает ограничиваться поцикловыми расчетами кинетики, главной проблемой которых является отсутствие достоверной исходной информации: ни на стадии приработки, ни на стадии стабильной работы накопленные деформации не могли быть корректно определены. Если предположить, что остаточные технологические деформации невелики по сравнению с ресурсом пластичности (что, очевидно, верно не всегда), а накопление деформаций в стабильном цикле в опасных зонах оценено на предыдущей стадии корректно, то такой расчет – с соответствующим поцикловым изменением диаграмм деформирования – может быть сделан, хотя и требует, как в предыдущем случае, дополнений к стандартным средствам пакетов МКЭ и обладает ограниченной информативностью.

Выводы

Полный «прямой» расчет процесса малоциклового деформирования конструкции в течение всего ресурса в настоящее время невозможен по 4 причинам:

• •    отсутствие экспериментальных данных для произвольного неупругого нагружения, характеризующегося ненулевыми размахами и приращениями пластической деформации в цикле (более того, отсутствуют стандарты таких испытаний);

• •    отсутствие моделей материала (физические «первопринципные» модели слишком сложны, а эмпирические не могут быть построены из-за отсутствия данных);

• •    отсутствие (в большинстве случаев) достаточно точной и полной информации о технологии и ее влиянии на свойства материала;

• •    трудоемкость и сложность обеспечения точности при расчете достаточно большого числа циклов.

Чернявский О.Ф.,                           Описание деформационных свойств материалов

Чернявский А.О.                                    при расчетах малоцикловой усталости

Деление процесса эксплуатации на стадии (приработка, стабильная работа, предразрушение) и явное выделение типов неупругого циклического деформирования (знакопеременное течение, одностороннее накопление деформаций, их комбинация) позволяет указать, какие из результатов ограниченных расчетов, проведение которых возможно в сегодняшних условиях, являются достоверными. Без такого деления обосновать достоверность результатов невозможно – пока не устранены все причины, перечисленные в п. 1.

Используемые в существующих пакетах МКЭ модели материалов требуют дополнения, поскольку погрешности, связанные с не учитываемыми ими факторами, могут быть значительны. В некоторых случаях такие дополнения удается обеспечить нестандартным использованием существующих в пакетах средств.