Описание изображений с использованием модельно-ориентированных дескрипторов

В ажным этапом решения широкого класса задач обработки, анализа, понимания и поиска цифровых изображений является выбор признаков, часто именуемых в современной литературе дескрипторами [1]. Существуют различны е классификации признаков, отражающие специфику подходов к их получению. Например, в монографиях [2, 3] признаки подразделяются на геометрические, топологические, вероятностные и спектральные. В работах [1, 4] локальные дескрипторы подразделяют на вероятностные, спектральные, спектрально-частотные и дифференциальные. Независимо от используемой классификации существуют признаки, которые могут сочетать в себе свойства, характерные для разных категорий. К таким дескрипторам относится модельноориентированный дескриптор, предложенный и развиваемый автором [4 – 6]. Его отличием от существующих является наличие априори заданного (или заранее определенного по обучающему множеству изображений) вероятностного распределения поля градиента, характеризующего модель анализируемого изображения и/или решаемую задачу. Признаком дескриптора является нормированная величина плотности вероятностей с аргументом в виде конкретного поля градиента. Она оказывается зависима как от реализации (конкретного изображения), так и от модели (распределения вероятностей), что позволило охарактери- зовать этот дескриптор как модельно-ориентированный (МО).

Характеризуя предлагаемый подход, следует отметить его особенности и отличия от других известных решений. Градиент в задачах распознавания и поиска изображений используется достаточно широко. Наиболее известными дескрипторами, основанными на вычислении градиента являются HOG [7] и SIFT [8] дескрипторы. Однако указанные и большинство других известных дескрипторов и признаков [1] не используют градиент изображения как векторное поле (используемая ниже интерпретация – комплекснозначное изображение/сигнал) полноценно. А именно: фазовая или амплитудная составляющая градиента в известных решениях игнорируется полностью или частично. Наиболее яркими примерами такого подхода являются работы [9– 12]. В частности, если в [9] фазовая составляющая градиента игнорируется полностью, то в работах [10 –12], наоборот, игнорируется амплитуда. Работа [12] вообще полностью посвящена методам и алгоритмам обработки специального подкласса изображений, характеризующегося только направлением изменения функции яркости, – так называемого поля направлений .

Попытки полноценно использовать многозначные (в том числе комплекснозначные) изображения предпринимались исследователями в различных направлениях. Например, в работе [13] был предложен специализированный многокомпонентный анализ; существует целый цикл работ по использо- ванию алгебры Клиффорда при работе с многокомпонентными изображениями (стр. 231–254 в [14]); статистическая обработка и анализ комплексных сигналов/изображений рассматривался в [15 – 18], а эссе по использованию гиперспектральных алгебр при работе с сигналами представлено в [19]. К сожалению, утверждать о возможности полноценной работы с многозначными (в данном конкретном случае комплекснозначными) изображениями в целях их анализа и распознавания невозможно. Данная работа представляет один из возможных подходов к использованию поля градиента для решения задач анализа и распознавания цифровых изображений.

Работа построена следующим образом. В первом параграфе даются основные определения и приводится краткое описание МО-дескриптора поля градиента, более подробное изложение можно найти в авторской работе [4], где также представлены несколько простейших параметрических моделей распределения вероятностей поля градиента и соответствующих признаков МО-дескриптора. Во втором параграфе представлена общая схема предлагаемого метода описания изображений с использованием МО-дескриптов. В третьем параграфе указанная общая схема детализируется: указываются алгоритмы предварительной обработки, вводится новая параметрическая модель МО-дескриптора и приводятся соответствующие ей признаки, предложен способ синтеза моделей МО-дескриптора. В заключительном параграфе представлены результаты исследования эффективности предлагаемого метода описания изображений на примере решения задачи распознавания лиц. Наконец, в заключение работы приведены выводы, благодарности и список использованной литературы.

Pg (g) min pG(g)

max p G ( g )

min Pg ( g )

arg g max Pg (g) arg g minmin pg ( g ) argg gl_ maxmin p8 (g) arg g |g|_ maxminps (g)

g arg g G min max p g argg g '• min max Pg (g)

I g| arg g max max pg (g)

V gl arggJ

,

каждая из которых отражает схожесть (в абсолютной величине) реализации градиентного поля с моделью по модулю, фазе и/или совместно. Причем для компонент этого вектора оказываются справедливыми ряд очевидных соотношений, например, min Pg (g)^ Pg (g)^ max Pg (g). (2)

Учитывая соотношения (2), признаки МО-дескриптора были определены как относительные положения компонент дескриптора (например, p_G ( g ) ) в

интервале от их минимального до максимального значений. Всего конструируются семь основных призна-

1. Модельно-ориентированный дескриптор поля градиента и его признаки

Пусть величина

g ( n_vn 2 ) , ( n_pn 2 ) e D ,

D = { ( n 1 , n ₂ ) : n 1 = 0, N 1 - 1, n ₂ = 0, N ₂ - 1 }

обозначает цифровое поле градиента (двухкомпонентное изображение), в котором каждый отсчет содержит информацию о градиенте в следующем виде: величина | g ( n 1 , n 2 )| определяет модуль градиента в соответствующей позиции, а направление (ориентацию по отношению к осям координат) вектора градиента в этой позиции определяет величина arg( g ( n 1 , n 2 )). Анализируемый фрагмент цифрового изображения цели-

ком обознается далее как

g = { g ( n , n ) },

^{L v          /J} ( n i, n 2 )^G D

а G –

случайное градиентное поле с плотностью вероятностей P g ( • ) , характеризующей модель наблюдения и/или решаемую задачу. Модельно-ориентированный дескриптор (МО-дескриптор) поля градиента g (де-

скриптор по отношению к модели G ) определяется в работе [4] как вектор из 11 компонентов вида

ков, конкретные выражения для которых приведены в работах [4, 5]. Вид первых трех признаков:

ф( Pg (g ))-Ф I min Pg (g) I V |g|               J u 0

ф

max P g ( g ) I ^- Ф ^ min P g ( g )

^ i =

ф ( P g ⁽ g ) ) ^- ^ ( ’mm i ⁿ P g ⁽ g ) )

Ф ( max P g arg g ^G

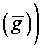
min p arg g

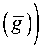
ф ( Pg ( g ) ) -фI minmin p₈ ( g ) I

⁴ G ⁷ V arg g g G J

^2 = "7-----------1— 7 ----------1,

ФI max max p₈ ( g ) I - ФI min min p₈ ( g ) I

V | g| arg g J V arg g |g|              )

где ф : R . ^ R - произвольная монотонно возрастающая функция. Признаки ^ i характеризуют степень похожести анализируемого градиентного поля на потенциально возможные реализации случайного поля G (на модель). Б о льшие значения означают б о льшую похожесть, а м е ньшие - м е ньшую. При этом если ^ ₀ , например, определяет степень схожести поля модуля градиента, то ^ 1 - степень схожести фазового рисунка и т.п. На все множество этих признаков ниже будем ссылаться как на вектор ^ = ( ^ 0 , ^ 1 , ^ , Ф 6 ) T . В работе [4] доказывается следующее утверждение:

V i = 0,6 0 <^ i <  1.

Имея ряд заданных случайных полей градиента

Gk (k = 0, K -1), для конкретного изображения можно рассчитать ряд анализируемого

нормированных

по диапазону признаков, например $ k ( k = 0, K - 1 ) , которые в совокупности его характеризуют. На основании полученных значений может быть произведен анализ обрабатываемого изображения и его распознавание. Примеры для нескольких простейших моделей случайных полей градиента, удобных для распознавания «каркасных» объектов, можно найти в предшествующих работах [4, 5].

• 2.    Общая схема предлагаемого метода описания изображений с использованием МО-дескрипторов

Общая схема описания изображения с целью их анализа и распознавания с использованием МО-дескрипторов представлена на рис. 1 (компоненты схемы, ограниченные пунктирной линией).

I _^^^^=^^^^_ I I Этап обработки I изображения

аначизируелюе изображение предварительная обработка

t —

расчёт полей градиентов предварительная обработка

♦

| синтез моделей |

наоор моделей

расчёт полей градиентов

> расчет признаков мО-дескрипторов

признаки МО-дескрипторов (по моделям)

Этап обучения/настройки

анализ/классификация

результат анализа

Рис. 1. Общая схема метода описания изображений с использованием МО-дескрипторов (пунктирная линия)

По аналогии со многими задачами распознавания и классификации изображений, процесс может быть поделен на два этапа: этап настройки/обучения и этап обработки (этапы на схеме ограничены штрихпунктирными линиями). На этапе настройки по обучающему множеству предварительно обработанных примеров-изображений рассчитываются соответствующие им поля градиентов, по которым синтезируется (формируется и настраивается) набор моделей дескрипторов – случайных градиентных полей Gk (k = 0, K -1). В рамках данной работы для синтеза моделей предлагается использовать метод главных компонент (PCA – Principal Component Analysis) над набором комплекснозначных гради- ентных полей [15 – 18, 20]. Из альтернативных способов, потенциально допускающих использование известных математических методов, можно указать также линейный дискриминантный анализ, метод независимых компонент, EM-алгоритм. Их сравнительный анализ выходит за рамки настоящей работы и может стать предметом отдельного исследования, как и разработка оригинального метода. Настроенные модели выступают на этапе обработки в качестве своеобразного «базиса» для анализируемых изображений. То есть позволяют описать анализируемое изображение в виде набора вещественных признаков ^k (k = 0,K -1) в диапазоне [0,1], характеризующих это изображение с точки зрения каждой из моделей. Эти признаки и используются в дальнейшем для анализа или классификации искомого изображения. А учитывая развитый математический аппарат обработки вещественных данных, анализ и/или классификация могут быть реализованы с использованием хорошо известных методов и алгоритмов: метода опорных векторов, деревьев решений и регрессии, нейронных сетей, ближайших соседей и др. (в данной работе при проведении экспериментальных исследований в качестве классификатора используется метод ближайшего соседа).

Следует отметить, что предлагаемый метод описания и анализа изображения использует идею бес-признаковых методов распознавания [21], поскольку анализируемый объект описывается через схожесть его с другими объектами, задаваемыми в виде случайных полей градиента G k ( k = 0, K - 1 ) .

Также следует отметить связь предлагаемого метода описания с рядом известных решений, в частности с дескрипторами HOG (histogram of gradients) [7] и SIFT (Scale Invariant Feature Transform) [8]. Оба эти дескриптора используют вектор (гистограмму), каждый отсчет которого определяет частоту появления в анализируемом изображении (для локальной обработки – фрагменте изображения) градиента определенной ориентации/фазы. Такой дескриптор является достаточно удобным и мощным средством анализа, распознавания и интерпретации изображений: обнаружения людей, распознавания номерных знаков и др. Достаточно очевидно, что отсчеты такого дескриптора по отдельности могут быть получены как значение первой компоненты МО-дескриптора для достаточно простой (зависящей только от фазовой составляющей) модели градиентного поля, характеризуемой пороговой величиной фазового рассогласования с предопределенной фазовой константой (константа определяет допустимые отклонения в направлении градиента). Очевидно, что такое решение могло бы быть улучшено, если модели МО-дескрипторов настраивать по обучающему множеству изображений. На взгляд автора, одним из возможных решений здесь может стать метод главных компонент, используемый ниже.

• 3.    Формальное описание предлагаемого метода

• 3.1.    Предварительная обработка

В рамках настоящего параграфа представлено более детальное описание основных блоков предлагаемого метода построения описания изображений с использованием МО-дескрипторов, указанных на рис. 1 (компоненты схемы, ограниченные пунктирной линией).

Данный шаг предлагаемого метода является опциональным и зависящим от задачи. В рамках экспериментов, описываемых ниже, использовалось два варианта предварительной обработки, описываемые известными поэлементными преобразованиями [2]:

• -    нормализация яркости и контраста,

• -    эквализация гистограммы.

В случае нормализации яркости и контраста функция яркости f (n1, n2) анализируемого изображения преобразовывалась по линейному закону f ("1,n2) ^ af ("1,n2)+ b

Плотность вероятностей отсчета конкретного градиентного поля зададим в параметрическом виде

P g ( „ , , „ ₂ ) ( g ( " i , " 2 ) ) =

a, > • exp ( " 1 , " 2 ) ^Г

= <

0,

Ig (

" 1 , " 2 )h^e ( " 1 , " 2 ) •

• |cos ( arg g ⁽ " 1 , "  2 ^)-ф ( " 1 , _n 2 ))|          ⁽⁵⁾

⁰ ^ | g ( " 1 , "  2 )| ^ g max ; |g ( " 1 , " 2 )| >  g max .

с такими параметрами a и b , чтобы среднее и выборочная дисперсия преобразованного изображения стали наперед заданными.

В случае эквализации гистограммы функция яркости f ( n 1 , n 2 ) анализируемого изображения преобразовывались по закону, напрямую зависящему от исходного (эмпирического) распределения P f (f o ) = P[f < f o ] функции яркости:

f ( "p " 2 ) ^ fпш +( fmax - fm n ) Pf [f ( "p " 2 )] .

Здесь, по аналогии с работой [4]: a ( n ₁, n ₂) – нормирующий множитель; p ₍ „ ₁, „ ₂) - величина, характеризующая степень «выраженности» градиента в соответствующем отсчете изображения, X - показатель степени (в работе использовались значения «1» и «2»); ф ( " ₁, " ₂) - величина, определяющая наиболее вероятное значение фазы градиента в соответствующем отсчете изображения; g max – наибольшее значение для модуля градиента на изображении.

Тогда значение плотности (4) имеет вид:

P g ( g ) = A ^exP

'Il ^{g (} " 1 , " 2 )|< , " 2) •

( " 1 , " 2 )       • Icos ( arg g ( " 1 , " 2

V VIх

^mln Pg ( g ) = A . arg g

Здесь

A =

^)-ф ( " 1 , " 2 ))|_?

Здесь f min , f max – требуемые минимальное и максимальное значения функции яркости итогового изображения. На практике обычно полагают: f min =0, f max = 255. Само распределение P f ( f 0 ) функции яркости оценивается по входному изображению.

• 3.2.    Расчет поля градиента

(

П a (

" 1 ^ " 2 ) '

" 1 , " 2 ) .

Полагая функцию ф : R + ^ R в виде

ф(x) =lnI x I, V A)

имеем признаки (3) в следующем виде:

По цифровому изображению f (n1, n2) градиентное поле g = { g ( ni, " 2 )}^2 ^ d может быть получено с ис-

пользованием любого известного способа, например, с использованием оператора Превитта [2].

• 3.3.    Модели градиентного поля, признаки МО-дескриптора

В качестве моделей будем использовать поля градиента с независимыми отсчетами [4]. Тогда плотность вероятностей конкретного градиентного поля G_k определена в виде:

^PG- ^{( g} ^( ,П. A ('-> < ^{g (} " 1 , " 2 ) ) • ⁽⁴⁾ где p_G k^„ 1, „ 2) ( - ) - плотность вероятностей градиента в конкретном отсчете ( n 1 , n 2 ) цифрового изображения. Дальнейшие рассуждения в этом пункте проведем для конкретного градиентного поля G_k , опуская соответствующий индекс: G .

^ 0 =

^ 1 =

E g ⁽ " 1 , "  2 )h^e( " 1 , " 2 ) • |^C0S ( arg g ⁽ " 1 , "  2 ^)-ф ( " 1 , " 2 ))|

( " Ъ " 2 )

g max E ^в " , " ₂ ) ^ cos ( arg g ( " 1 ^, "  2 ) — ^Ф ( "₁," ₂ ) )

( " 1 , " 2 )

E g ⁽ " 1 , " 2 )h ^e( " 1 , " 2 ) ^ cos ( arg g ⁽ " 1 , " 2 ^)-ф ( " 1 , " 2 ) )

( " 1 , " 2 ) ______________________________________________________________________________ (7)

E |g ⁽ " 1 , "  2 ^ •З "„, " 2 )                    ,

( " ₁, " ₂ )

E |g ⁽ " 1 , "  2 )K "„ " 2 ) • cos ( arg g ⁽ " 1 , "  2 ^)-ф ( " , " 2 ) ) ( " ₁, " ₂ )

^ 2 =

.

g max / j P( " 1 , " 2 ) ( " 1 ^ " 2 )

Любую из этих величин или все вместе можно использовать в качестве признака изображения. Величина ^ 1 , используемая в работе далее, принимает тем б о льшее значение, чем ближе фазовые составляющие модели и анализируемого поля градиента в отсчетах с высокой степенью «выраженности».

• 3.4.    Настройка моделей: метод на основе PCA

Для проведения расчета признака ^ k (7) по каждой из моделей G k ( к = 0, K - 1 ) необходимо в процессе обучения (настойки) системы определить набор числовых параметров р^ n ) ф к _п n ) . Для этого предлагается использовать метод главных компонент (PCA – Principal Component Analysis). Специфика его использования в данной работе заключается в том, что данные представляют собой набор комплекснозначных градиентных полей [15].

Для удобства изложения представим двумерное комплекснозначное поле g ( n 1 , n 2 ) в виде одномерного комплексного вектора v с компонентами v ( n ), положив, например:

v ( n 1 N 2 + n 2 ) = g ( n 1 , n 2 ) .

Суть метода главных компонент, как известно [15– 18, 20], состоит в построении оптимального в смысле ряда критериев (в частности, по критерию среднеквадратической ошибки представления) разложения исходного набора из M векторов { V m } M ¹ по новому базису - векторам { e_k } K J ( K <  M ) (т.н. преобразование Кархунена–Лоэва):

K-1                       __________ vm = E Ymek + vE , m = 0, M - 1.                (9)

к = 0

Здесь вектор v _E – вектор средних для комплекс-

M ^{- 1}

ных векторов { V m } _m = 0 . Заметим, что, поскольку исходные вектора комплексные, получаемый базис также оказывается комплексным, так же как и коэффициенты разложения у m .

Базис { e_k } K ¹ - суть собственные векторы эрмитовой (выборочной) матрицы ковариации C

M - 1                         T

C = E (vm - vE )(vm - vE )

m = 0

исходного множества центрированных векторов, соответствующие K наибольшим собственным числам (у эрмитовой матрицы все собственные числа % к вещественны):

C e_k =% _ke_k , к = 0, K - 1.

В выражении для матрицы C символ T – знак транспонирования соответствующего вектора.

Получив базис { e_k } K ¹ представления комплекс-

M ^{- 1}

ных векторов { V m } m = 0 и соответствующих полей градиента и учитывая связь компонент векторов и отсчетов двумерных полей в виде (8), параметры моделей (5) предлагается задать следующим образом:

n 2 ) = l e k ⁽ n 1 N 2 ⁺ n 2 )| ,

^ kn , . n ₂ ) = arg ( e k ( ⁿ 1 N 2 ⁺ n 2 ) ) , ^k = ⁰, ^{K -} 1. ⁽¹⁰⁾

Число K , определяющее количество используемых моделей дескрипторов, в конкретной задаче может выступать как независимый или зависимый (например, от точности представления (9)) параметр.

• 4. Экспериментальное исследование предлагаемого метода описания

  Исследование эффективности предложенного описания изображений с использованием МО-дескрипторов проводилось на примере решения задачи распознавания лиц [22]. В качестве тестовых данных использовались изображения лиц базы данных «Extended Yale Face Database B» [23, 24]. По информации разработчика базы данных, указанной на сервере « http://vision.ucsd.edu/datasetsAll» , база данных содержит в целом 16128 изображений 28 человек, снятых с 9 позиций при 64 вариантах освещения, также для каждого человека присутствует один дополнительный снимок (65-й). По факту, доступный на официальном сайте архив размером 57123 Кб содержит данные при 64 вариантах освещения для 38 персон. Поскольку часть файлов повреждена, доступными для экспериментов являются 2420 изображений 38 персон.

Следует также отметить, что, несмотря на значительное число работ по решению задачи распознавания лиц с использованием различных методов классификации и подходов, использовать результаты какой-либо из них для выполнения корректного сравнения (то есть сравнения выбранных представлений и/или методов классификации в одних и тех же условиях) оказывается довольно затруднительно: авторы используют различные методы предобработки, различные фрагменты исходных изображений, различные подмножества тестовых баз данных, различные методы обучения (при обучении может быть один объект в классе, несколько в классе, может использоваться или не использоваться метод кросс-валидации, подвыборки могут быть детерминированные или случайные и др.) и оценки показателей эффективности, различное подмножество признаков описания и т.п. В результате показатели качества распознавания в работах варьируются даже для одной тестовой базы от, например, 0,54 (стр. 32 в монографии [22]) до практически идеального распознавания.

Учитывая все вышесказанное, для оценки эффективности предлагаемого подхода описания изображения представляется целесообразным проведение идентичных экспериментов по распознаванию и сравнению получаемых результатов с существующим методом-прототипом. Поскольку для синтеза модели в предлагаемом подходе применялся метод PCA, сравнение проводилось с «классическим» методом «собственных лиц» [25]. То есть прототипом описания являлись коэффициенты разложения полутоновых изображений по базису, получаемого методом главных компонент [20, 22, 25].

Для определенности, эксперименты проводятся при следующих условиях, позволяющих проверить получаемые в итоге результаты:

• -    тестовая база данных содержит 2420 изображений для 38 персон (см. описание исходных данных выше);

• -    изображения использовались с пониженным разрешением, то есть вместо исходных изображений размера 192×168 использовались картинки 96×84, полученные заменой каждого фрагмента 2×2 на единственный отсчет с усредненным значением яркости;

• -    из 64 изображений для каждого человека первые 32 изображения используются для обучения (настройки), а последующие 27 – для оценки показателей распознавания;

• -    в сопоставляемых подходах используется один и тот же метод предварительной обработки (варианты: нет предобработки, нормализация яркости и контраста, эквализация гистограммы), который применялся до снижения разрешения изображений;

• -    в качестве классификатора использовался метод ближайшего соседа с евклидовой метрикой;

• -    качественные показатели сопоставлялись при одинаковом количестве признаков-описателей (вещественных);

• -    в качестве показателя качества выступало относительное число верно классифицированных изображений (1026 изображений по 38 классам).

Примеры комплекснозначных «собственных лиц», получаемых методом PCA и используемых для синтеза моделей МО-дескрипторов, для различных вариантов предварительной обработки представлены на рис. 2. Цвет характеризует локальную ориентацию поля градиента, яркость – его амплитуду. При этом красный и синий цвета соответствуют противоположным (вертикальным) направлениям градиента. Фиолетовый, таким образом, соответствует горизонтальному направлению.

НЕВ

EBB

а)

б)

Рис. 2. Примеры комплекснозначных «собственных лиц».

Варианты предварительной обработки: отсутствует (а); эквализация гистограммы (б)

Собственно показатели качества решения искомой задачи приведены в табл. 1–3. В последнем столбце («выигрыш») указана величина (в процентах) относительного роста качественного показателя, вычисляемая как отношение величины приращения показателя качества к его значению для метода-прототипа.

Табл. 1. Относительное число верно классифицированных объектов: нет предварительной обработки

Число признаков	Показатель качества
	Прототип	Признаки МО-дескрипторов	Выигрыш (%)
2	0,0419	0,0564	34,61
4	0,0848	0,1901	124,17
8	0,2098	0,3333	58,87
15	0,3168	0,4561	43,97
50	0,4347	0,582	33,89
100	0,4737	0,6199	30,86

Табл. 2. Относительное число верно классифицированных объектов: нормализация яркости/контраста

Число признаков	Показатель качества
	Прототип	Признаки МО-дескрипторов	Выигрыш (%)
2	0,0395	0,0741	87,59
4	0,0593	0,2160	264,25
8	0,1741	0,4136	137,56
15	0,2901	0,5099	75,77
50	0,3802	0,5988	57,50
100	0,4173	0,6716	60,94

Табл. 3. Относительное число верно классифицированных объектов: эквализация гистограммы

Число признаков	Показатель качества
	Прототип	Признаки МО-дескрипторов	Выигрыш (%)
2	0,0395	0,1321	234,43
4	0,0728	0,3642	400,27
8	0,2198	0,4728	115,10
15	0,3753	0,7148	90,46
50	0,5074	0,9049	78,34
100	0,5457	0,9247	69,45

По представленным результатам исследования можно сделать следующие выводы:

• -    предлагаемый метод описания изображения с использованием МО-дескрипторов стабильно дает более высокие показатели качества при любом количестве признаков и любом способе предварительной обработки (выигрыш всегда положительный),

• -    наилучшие качественные показатели предлагаемый метод (так же, как и метод-прототип) демонстрирует для случая предварительной обработки путем эквализации гистограммы (см. табл. 3);

• -    б о льший (относительный) выигрыш достигается при меньшем числе признаков;

• -    выигрыш предлагаемого метода по сравнению с методом-прототипом всегда существенен. Минимальный выигрыш для всех экспериментов оказывается 30 % (100 признаков и отсутствие предварительной обработки – табл. 1), максимальный – 400 %, то есть качество решения задачи возрастает в 4 раза ! Для наилучшего результативного варианта предварительной обработки (эквализация, табл. 4) рост показателя качества всегда оказывается не менее 70 % !

Обобщая представленные выше промежуточные выводы, отражающие детальный анализ результатов, можно говорить о значительном приросте качественных показателей при использовании предло- женного метода описания изображений с использованием признаков МО-дескрипторов по сравнению с методом-прототипом.

Выводы и рекомендации

В работе предложен и исследован метод построения описания изображения с использованием модельно-ориентированных дескрипторов. Метод предполагает построение описателей анализируемого изображения на основе сопоставления фактического поля градиента этого изображения с моделью МО-дескриптора. На примерах решения практической задачи распознавания изображений лиц продемонстрировано значительное и стабильное преимущество предлагаемого метода описания по сравнению с методом-прототипом, использующим тот же математический принцип (метод главных компонент) при обработке полутоновых изображений.

Разработка оригинального алгоритма синтеза моделей МО-дескриптора может являться дальнейшим направлением работ в этой области.

Исследование выполнено при финансовой поддержке:

• -    грантов РФФИ в рамках научных проектов № 15-07-01164-а, № 17-29-03190-офи-м;

• -    программы фундаментальных исследований Президиума РАН «Фундаментальные проблемы информатики и информационных технологий».

В качестве тестовых данных использовались изображения лиц базы данных «Extended Yale Face Database B» [23, 24].