Описание математической модели тепловых процессов в системе электрод - деталь - теплоотводящая масса при определении параметров восстановления дисковых рабочих органов

Эффективность метода восстановления режущей кромки дисковых рабочих органов почвообрабатывающей и посевной техники определяет целесообразность практической реализации его в производстве. Предложенный метод электромеханического деформирования совмещающего в себе процессы термического и силового воздействия на режущую кромку при восстановлении рабочих органов сельскохозяйственных машин отвечает выполнению данных требований [1, 2].

Диски посевных и почвообрабатывающих орудий имеют различные конструктивные параметры и свойства материалов, из которых они изготовлены, поэтому требуется большой объем экспериментальных исследований, необходимых для определения параметров и режимов процесса восстановления режущей кромки этих деталей. Число проводимых натурных экспериментов может быть уменьшено за счет численных экспериментов, осуществ- ляемых методами математического моделирования.

Процесс формирования режущей кромки диска определяется давлением электрода и достижением необходимой температурой нагрева металла в области деформирования, соотношение которых определяет эффективность процесса электромеханического деформирования. К основным технологическим параметрам определяющим величину энерговложения можно отнести: давление Р, электрическое напряжение U , и силу тока I. Для установления между ними взаимосвязи в процессе ЭМД будем использовать методы математического моделирования тепловых процессов.

На рисунке 1а показана схема электромеханического деформирования, поперечный разрез системы и введена система координат для расчета температурных полей; на рисунке 1б показан вид системы в плане.

Рис. 1. Схема электромеханического деформирования режущей кромки диска почвообрабатывающего орудия с использованием электроконтактного нагрева

1-формующий электрод; 2- восстанавливаемый диск; 3- теплоотводящая масса; l 1 -высота электрода; l 2 -средняя толщина восстанавливаемого участка режущей кромки до и после деформирования; l 3 -толщина теплоотводящей массы.

Деталь (диск 2) жестко закрепленная на теплоотводящей массе 3, с определенной угловой скоростью го подается под формующий электрод 1, к которому приложено давление Р и напряжение U . Между электродом и восстанавливаемой деталью образуется тонкая переходная зона, имеющая сопротивление R , преодолеваемое электрическим током с выделением теплоты. Полученная теплота расходуется на нагрев электрода и детали.

Выделение тепловых процессов в качестве основных, влияющих на процесс восстановления режущей кромки, позволил перейти от анализа тепловых процессов в реальных системах «электрод–деталь– теплоотводящая масса» и «деталь-теплоотводящая масса» к тепловым процессам в условно выделенных составных стержнях рассматриваемых процесс ЭМД в статическом режиме, когда процесс электромеханического деформирования осуществляется без вращения диска ( го =0).

Удельную мощность q (плотность теплового потока) определим выражением [3]:

U ⋅ I q = ^ 1^^’       ⁽¹⁾

где U - падение напряжения на контакте, В;

I - сила тока в контакте, А;

S - площадь пятна контакта, м²;

k i -коэффициент энерговложения, учитывающий особенности контактного взаимодействия электрода с восстанавливаемой деталью.

Математическая модель теплопереноса в стержневой системе (рис.2) определила для каждого из элементов трехслойной системы следующие уравнения теплопроводности:

дт      д2 тх с, р--= р —-11 д t    1 дх2

д Т 2

с 2 Р 2  -     ^р 2

∂t д2 Т2

д х ²  ’

д Т       д ² Т₂

с Р — = Р —1 ³³ д t     ³ д х ²

’

0 i , 0max, (2)

0 2 , 0max, (3)

, l 2 2 +I 3 , 0 max , (4)

где c i - удельная массовая теплоемкость;

p i - плотность;

k i - коэффициент теплопроводности i -ой области ( i = 1’2’3);

t_max - время завершения процесса деформирования режущей кромки в статическом режиме ЭМД.

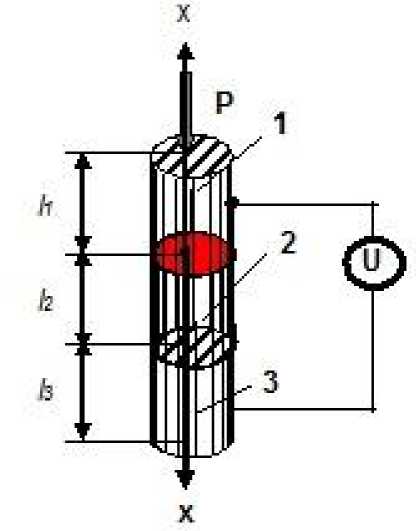
Рис. 2. Составной стержень эквивалентный в тепловом отношении трехслойной системе электрод (1)-деталь (2)-теплоотводящая масса (3)

Уравнение теплового баланса на границе «деталь - электрод» представим в следующем виде:

ат. и j

- Я —¹ = ^ 2 -2- + к 1 -— , х =0, 0< t < t max ,(5) ∂ х ∂ х S

Уравнение теплоотдачи с поверхности электрода запишем на основании закона Ньютона:

∂ Т

— Я —— — a(Tj — -ср ), x=li, 0

Условие непрерывности температурных полей и тепловых потоков на границе раздела «деталь - теплоотводящая масса» в случае идеального теплового контакта имеет следующий вид:

ат.     ат. _ _    . _

Я₂^-Т^ — Я     , -2 = -3, X=12. 0<tmax,

∂х      ∂х

Условие теплоотдачи с поверхности теплоотводящей массы опишем следующим уравнением:

-

∂Т

Яз —- — qomc , Х=Ъ + 13 ,0

Начальные условия процесса (начальное распределение температур) зададим следующим образом:

-i = Tcp; 0<x<li; 02+ I3; i=1,2,3; t=0. (9)

Таким образом, система уравнений (1)(8) представляет собой одномерную математическую модель тепловых процессов в системе электрод-деталь-теплоотводящая масса в статическом режиме ЭМД.

С ее помощью могут быть решены две задачи: 1) задача определения коэффициента энерговложения к1 по данным натурного эксперимента процесса ЭМД в статическом режиме (задача идентификации); 2) задача вычисления температурного поля составного стержня, состоящего из контактирующих стержней электрода, детали и теплоотводящей массы (задача моделирования).