Описание образа одного оператора типа потенциала с осциллирующим ядром

Рассматриваются операторы типа потенциала

0 i|t|

(к т ^)(x) =           \ ^(x - 1) dt, t 0 = t-                   (i.i)

| t |                                                                                   | t |

Rn где 0 < Re a < n/2, Ym(t0) — неэллиптическая сферическая гармоника m-го порядка.

Получены ( L _p - L _q )-оценки для оператора K _m ^α . Методом аппроксимативных операторов (АОО) построено обращение потенциалов (1.1) с L p -плотностями и дано описание образа K mm (L p ) в терминах обращающих конструкций. Это описание, содержащееся в теореме 2.2, является основным результатом статьи.

Заметим, что рассматриваемый случай является неэллиптическим: в нем символ оператора (1.1) вырождается на конусе нулей однородного многочлена Y _m (t).

В настоящее время имеется ряд работ по обращению операторов типа потенциала в неэллиптическом случае в рамках L p -пространств (см. книгу [19], обзорные статьи [16–18] и имеющуюся там библиографию). Однако описать образы таких потенциалов удавалось редко и, как правило, для операторов специального вида. Для операторов вида (1.1) до сих пор оставался открытым даже случай m = 1 (хотя, обращение этих операторов было построено в [5]). Возникающие здесь трудности принципиального характера связаны с вопросом о плотности в L p пространства Ф v типа Лизоркина, построенного по множеству нулей символа рассматриваемого оператора (см. замечание 4.1).

Эти трудности удалось преодолеть при 0 < Re a < n/2, используя (L p — L q )-оценки для оператора K _m ^α , полученные в теореме 2.1. Заметим, что аналогичный подход использовался в [12] в случае радиальных характеристик, т. е. характеристик принципиально иной природы.

Отметим также, что при доказательстве теоремы 2.1 мы получаем представляющие самостоятельный интерес (L p — L q )-оценки для операторов Бохнера — Рисса B ^Y комплексного порядка y , Re Y > 0, играющих важную роль в различных вопросах анализа. Эти оценки содержатся в теореме 3.1. Ранее утверждение этой теоремы было известно в случае Im y = 0 (см. замечание 3.1).

• 2.    Основные результаты

  • 2.1.    ( L p — L q ) -оценки для оператора K m . Через (A, B, ...,K) будем обозначать открытый многоугольник с вершинами в точках A,B,...,K ; [A, B, ..., K ] — его замыкание; L ( A) — L -характеристика оператора A , т. е. множество всех пар (1/p, 1/q) для которых оператор A из L p в L q ограничен.

Пусть 0 < Re а <  n/2. Рассмотрим следующие точки на (1/p, 1/q)-плоскости:

. Л    Re а\

^A = R1^—   /

C / 3  2 Re а 3  2 Re а

= к 2 - n — 1 ’ 2 - n — 1

A0 '        1 o) •

C 0   / 2 Re а 1 2 Re а 1

= k n — 1 — 2 ’ n — 1 — 2

G =

/    (n — Re а)(п — 1)

V1        n(n + 3)     ’

-

Rna } , G 0 = (

Re а (n — Re а)(n

, n

n(n + 3)

)•

H =

-

Re а

’ 1 n

Re а

-

n

,

H 0 ^R

n

Re а n

,

/ 2(Re а + 1)1 1

V n + 12’ 2

/1 3 2(Re а + 1)

V 2 ’ 2

E^w F=(!• I)-

O = (1,1),    O' = (0’ o).

Нам понадобятся следующие множества (см. рисунки 1 и 2):

L l (а’ n) = <

'[A ' ,H 0 ’H’A’E] \ ([A ' ,H ' ] U [A,H]),

(A ' , G, C 0 , C, G, A, E) U (A, E] U (A ' , E ) U (C 0 , C ), (A ⁰ , G ' , F, G, A, E ) U (A, E] U (A ⁰ , E) U {F } , (A’G’F’G’A’E ) U (A,E] U (A’E),

, (A ⁰ , G, K', K, G, A, E ) U (A, E ] U (A ⁰ , E ) U [K 0 , K ],

0 < Re а 6 n ( n-8 ’ n ( n^-1 ) <    _n< n - l

2( n +1) < ^{Re а}<  2 ’

Re а = n^-1 , Im а = 0, а = n-¹ ’ n^-1 < Re а <  ⁿ ’

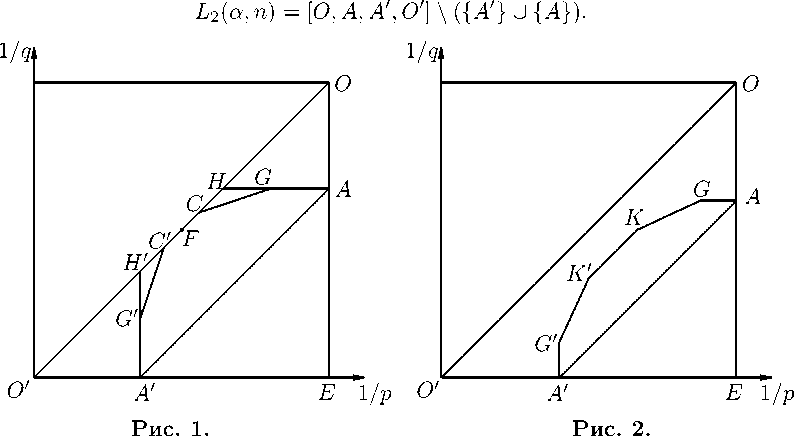
Следующая теорема описывает выпуклые множества (1/p, 1/q)-плоскости, для точек которых оператор K _m ^α ограничен из L p в L q (см. рисунки 1 и 2).

Теорема 2.1. Пусть 0 < Re a < n/2. Тогда справедливо вложение

L(K m ) Э L ₁ (a, n) П L ₂ (a, n).

Замечание 2.1. Заметим, что для (n — 1)/2 < Re a (за исключением некоторых значений α) оценки для оператора K_m^α , а также для более общего оператора вида (1.1) с произвольной однородной характеристикой 6(t') (вместо Y_m(t⁰)), гладкой в Rn\{0}, были получены в [8] с помощью другого метода, который не работает в случае Re a 6 n^-1•

Результат, содержащийся в теореме 2.1 при (n — совпадает с полученным в [8].

• 2.2.    Описание образа K m (L p ). Пусть k m (£)

Введем оператор

1)/2 < Re a < n/2 (см. рисунок 2),

— символ оператора K _m ^α (см. п. 3.4).

где

( ^L P.m ) ( L 2 )

H ^a f = lim lim hY * f, • 0 5^ 0 ^e’^d

.       —             ■.

• (2.1)

h a^ (t) = F ^-1 (

km :.       :

-

1) ' e -²

( | k m O² + iW I ² + (e + i) ² ) '

' > Re a (2[n/2] + 1) + [n/2](3 — n) + 3 — (n —

L p,p = {f(x) : j | f(x) | ^p (1 + \x\) ^ dx< to

J (t), 1)/2, } •

• (2.2)

Следующая теорема дает описание образа Km(Lp) в терминах оператора Hа, явля- ющегося левым обратным к потенциалу Kmα .

Теорема 2.2. Пусть 0 < Re a < n/2, a = (n — 1)/2, (n — 3)/2,... Предположим, 2(Re a + 1)/(n + 1) — 1/2 6 1/p < 1 при (n — 1)/2 < Re a < n/2 и 1/2 6 1/p < 1 0 < Re a < (n — 1)/2. Тогда что при

α

m

Km(Lp) = {f е Lq : Haf E Lp} , где Ha — оператор (2.1), q — произвольное число такое, что 1 < q 6 2 и оператор ограничен из Lp в Lq в соответствии с теоремой 2.1.

• 3.    Вспомогательные сведения и утверждения

  • 3.1.    Обозначения. Пусть hf,u) = JR n f (x)w(x)dx; W _e y — ядро Гаусса — Вейер-штрасса; R o = { у : у = Ff,f E Li} — винеровское кольцо функций; Lp — класс ядер k E S 0 таких, что kk * f k q 6 C k f k p , где f E S , константа C >  0 не зависит от f ; M p = F(Lp) — класс (p — q)-мультипликаторов. Классы Lp и M p были введены Л. Х¨ермандером в [10].

• 3.2.    Об одном (р — q) -мультипликаторе . Обозначим

Пусть далее V — произвольное замкнутое множество в R n . Обозначим Ф v = {ф E S : (D ^v ф)(£) = 0, £ E V, | v | = 0,1,... } , Ф v = { у E S : <у E Ф v } . Пространства Ф v и Ф v были введены и изучены С. Г. Самко в [6, 7], см. также книгу [19]). В случае, когда V — совокупность всех координатных гиперплоскостей, указанное пространство изучалось П. И. Лизоркиным (см. [3]).

Пусть функции ш(г), к (г),х(г) E C “ (0, го ) таковы, что 0 6 ш(г), к (г), х(г) 6 1, ш(г ² ) = 1, если r | 6 1 — 6/2, w(r² ) = 0, если r >  1 — 5/4; к (г) = 1, если | 1 — r | 6 5/4, к (г) = 0, если | 1 — r | > 5/2; x(r) = 1, если r >  1 + 5/2, x(r) = 0, если r 6 1 + 5/4.

Выбором 6 (0 < 5 < 1/2) мы распорядимся при доказательстве леммы 3.1. Предположим также, что ш(г2) + к(г) + х(г) = 1

b a (iei) = к (^М а- n- 1 (1 — | е | + i0) n- 1 ^{- a} , a = n — , n ₂³, ...,         (3.1)

A \ = (2n) ^-n e ^- in ^(Л+1) Г(А + 1). При доказательстве теоремы 2.1 существенно используется следующая

Лемма 3.1. Пусть 0 < Re a <  n/2, a = (n — 1)/2, (n — 3)/2,... Тогда

(3.2)

baC^D e M pq ,   ^(1/p, 1/q) e L i ^(a,n).

C В статьях [12-14] показано, что ядро s _a (t) = x( | t | ) | t | ^a-n e i^|t| принадлежит L p , если (1/р, 1/q) G L i (a,n), следовательно, с(£) G M pq для указанных р и q. Кроме того, в [11] и [12] было получено следующее представление для c(£) в окрестности единичной сферы:

(3.3)

K(|e|)sa«)= ba(|^)P (|€|)+ K(|e|)ua«), где P(x) — бесконечно дифференцируемая функция, для которой P(1) = 0, к(|£|)иа(£) G Mpq, если (1/р, 1/q) G [O0, O, E]. Выберем 5, участвующее в определении функций ш, к, х (см. п. 3.1) так, чтобы нули функции P(|£|) не принадлежали supp к(|^|). Тогда разделив (3.3) на P(|£|), из полученного равенства имеем (3.2). B

• 3.3.    Оценки для оператора Бохнера — Рисса комплексного порядка с неотрицательной вещественной частью . Указанный в заголовке оператор определяется в образах Фурье равенством

—Y(7 -Vni2

B Y^ =   _Г(1 + _Y) (1 — ^²)+^), Re Y > 0

(см. [20, гл. 9, § 2]). Для него справедливо интегральное представление

^{(B Y} ^^)(x) = R n ^|y^{| Y 2} J n +y⁽ЫЫ ^{х —} y)dy,

(3.4)

где J _v (z) — функция Бесселя порядка v.

Следующая теорема содержит (L _p — L _q )-оценки для оператора (3.4).

Теорема 3.1. Пусть 0 6 Re y < (n — 1)/2. Тогда справедливо вложение

L (B ^Y ) D L i f— y + n — ' ,n).                          (3.5)

C Представив J n + y (z) в виде линейной комбинации функций Ханкеля

J n + y (z)=1 (H n + Y (z)+ H n ² + Y (z))

и воспользовавшись интегральным представлением из [4, стр. 165] для H V 1) (z) и h V²⁾ ( z ) , оператор (3.4) запишем в виде

(B ^Y ^)(x) = (M + ^)(x) + (M - ^)(x) + (N ^Y ^)(x),

(3.6)

где

(M±y)(x) = C±j x(|y|)|y| n^ Ye±i|y|m±(|y|)^(x - y) dy, Rn i             1 । in(n+l+2Y)    1 /n + 1      \

C ± = (2n) ^{- 2} e ±    4    r ^-1 — + y) ,

ОО                                        n— 1 + y, m±(|y |) = I e - t n-1+Y (1 ± 2y)       dt;

⁽N ^Y y^)(x) = j^{(1 -} хСЫ^Ы - ² -^Y J 2 +y⁽ЫМ^{х -} y) dy.

R ⁿ

Характеристики m±(r) удовлетворяют условиям теоремы 4.2 из [14]. Применяя эту тео- рему, получаем

L(M ± ) dl(-y + n - ' ,n).

(3.7)

Кроме того, очевидно, что

L (N ^Y ) = [O 0 , O, E ].

(3.8)

Из (3.6)–(3.8) следует (3.5).

Замечание 3.1. Отметим, что в случае вещественных y > 0 утверждение теоремы 3.1 можно получить интерполяцией между оценками, полученными в [20] (см. утверждение на стр. 390) и замечании 2 из [9].

Замечание 3.2. Нам понадобится также результат для оператора (3.4) в случае - 1/2 < Re y < 0, полученный в [14]. Именно, в [14] было доказано, что вложение (3.5) справедливо для таких γ .

• 3.4.    Вычисление символа оператора K m . Обозначим k m_e (x) = Y m (x ⁰ )e ^{i|x| e|x|} | x | ^{a n} Переходя к полярным координатам и применяя формулу Функа — Гекке (см. равенство (1.60) из [19]), получаем

∞ 1

к£«) = | S ^n-1 | Y m (^) I .         dp j (1 - y ² ) n— ³ Pm (y)e i^{p |}^ y dy,

0                  - 1

где Pm(y) — многочлен Лежандра. Применяя далее к внутреннему интегралу последовательно формулы 7.321 и 6.621 из [1], имеем d,К) = Сп^')|4|mF (a^2m,a + m+1; 2 + m; -(^l-!^) ,

(3.9)

где

ε m,n

,_{n- 1} 1    ni ^m r(n - 2 + т)Г(а + m)

| m!2mr(n-2)Г(2 + m)(e - i)a+m а F(a, b; c; z) — гипергеометрическая функция Гаусса.

Пусть | ^ | < 1. Переходя в (3.9) к пределу при е ^ 0, будем иметь

С «) = C m„ Y _m ^^⁰)|^| m F a^^m¹ , 2+22+1; 2 + m; | ( | ²) .        (3.10)

Пусть | e | > 1. Применяя к гипергеометрической функции в (3.9) формулу (12) из [4, стр. 219], и переходя затем к пределу при е ^ 0, получаем

СЮЦ» _ Сс у (,.)        ■ m + "Жи/У km(e) = CmnYm(e )^((а + т + 1)/2)Г((т + n — а)/2)

×

| e | -a _F ( ^{а + т а — т}

-

—^lei ^-2)

+

Г(т + п/2)Г( — 1/2)

(3.11)

Г((а + т) /2)Г((т + n/2 — (а + т + 1)/2)/2)

×

i e | ^-a-1 F(

а + т + 1 а — т —

,

^^±^;|; 1 4Г ²

.

Нетрудно показать, что при 0 < Re а < n/2 справедлива формула для преобразования Фурье в слабом смысле:

⁽K m ^^)(x) =

(2n) ^{- n} /

R

k m :.:••/:,

ϕ ∈ S .

(3 . 12)

• 4.    Доказательство основных результатов

  • 4.1.    Доказательство теоремы 2.1. Имеем

km(e) = mei2) ka(e) + K(iei)km(e)+x(iei)km(e) = km,o(e) + km,1(e) + km^(e).(4.1)

Очевидно, что km,o(e) e Mp, (1/p, 1/q) e [O0,O,E].(4.2)

Кроме того, из соотношения x(iei)ie|-a e Mpq, (1/p, 1/q) e L2(a, n), доказанного в [15], вытекает, что km,^(e) e Miq, (1/p, 1/q) e L2(a,n).

Рассмотрим kd1(e). Применяя к гипергеометрическим функциям в (3.10) и (3.11) формулу (11) из [4, стр. 219], представим km 1(e) в виде n-1

km,i(e) = K(iei)(1 — iei2)+2 asa(e)+ba(iei)sa(e)+ra(e),(4.4)

где ba(iei) — функция (3.1), ra(e),s“(e) e C0^ (j = 1, 2). Тогда km, 1(e) e Mpq, (1/p, 1/q) e L1 (а,п),(4.5)

в силу теоремы 3.1 и леммы 3.1.

Из (4.1)–(4.3) и (4.5), на основании (3.12) получаем kKm^kq 6 Ck^kp, (1/p, 1/q) e L1(а,n) П L2(а,n), ^ eS.(4.6)

С учетом теоремы С. Л. Соболева, оценка (4.6) распространяется на функции ϕ ∈ L p , 1 < p < n/ Re а.

• 4.2.    Доказательство теоремы 2.2. Вложение

  (4.7)

  
  

Km(Lp) c {j e Lq : Haj e Lp} вытекает из теоремы 2.1 и равенства

(h акт ^) (x) = ^(x), которое доказывается так же, как в [11, 12] в случае потенциалов с радиальными характеристиками.

Докажем вложение, обратное к (4.7). Предположим, что f ∈ L _q , H ^α f ∈ L _p . Пусть функция ш e S такова, что ш (£) = 0 в некоторой окрестности множества V = { ( : k m (£) = 0 } и S n^-1 (следовательно, ш e Ф _V ).

Легко показать, что hKmH ■„■ = hH af,Km ш^

где Km оператор с символом km(£). С учетом (4.8) имеем hKmH aj>i = lim ^hfH" Km шi,(4.9)

где H _ε ^α _,δ — оператор свертки с ядром (2.2). Воспользовавшись равенством

^(H“ ₅ ^K m ^ш)(х) = ^(А е ^{ш)(х) + i6 (K} e,8 W _e/ 2^^(x),                 ⁽4.1⁰⁾

где K _ε ^α _,δ — оператор с символом

(|£|2 -

,

( | km«) | 2 — iW I ² + (s - i) ² ) '

с учетом (4.9) имеем hKmHaj,шi = lim hj,AEш^ + lim lim hf,i5Ke,5We/2шi.             (4.11)

ε → 0           ε → 0 δ → 0

Докажем равенство

(4.12)

Y i m ₀ hf,i5K _e,₅ W _e/ 2 шi = 0.

Очевидно, что (Ke,sWe/2ш)(^) e Фv. Следовательно, hf,i6Ke,5 We/2шi = (2n)-n hFj,i5F (Ke,5 We/2ш)i, где F j понимается в смысле ФV-распределений; это преобразование Фурье совпадает с преобразованием Фурье в смысле Lq0 (в соответствии с теоремой Хаусдорфа — Юнга). Применяя неравенство Г¨ельдера, имеем

\hf,i5K _e,₅ W _e/ 2 ш i | 6 C^ k Fj k q 0 X

e2^j№_-j_^qjsw

Ik m (№ Ш² + (s - i) ² i 'q

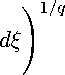
(4.13)

Заметим, что интеграл в правой части (4.13) конечен. Переходя в (4.13) к пределу при 6 ^ 0, получаем (4.12).

В силу (4.11) и (4.12) имеем

• ²-    П'е—<12 h K m Hfc = Jrn ^(2n) -n hf, (^2 + 1 - i)^ ^WO j = hfM

Таким образом, мы пришли к равенству hKmH aM = hf,w).                         (4.14)

Переходя к завершающему этапу доказательства, для заданной функции ϕ ∈ S выберем последовательность { w j } , W j E S такую, что W j (£) = 0 в некоторой окрестности ( L q0 )

множества V и lim W j = у. Существование такой последовательности доказано в [7] j -^

(см. также [19, гл. 2]).

На основании (4.14) имеем hKm н -.■ i = hf,Wj i.

Переходя в этом равенстве к пределу при j → ∞, получаем hf,^i = hKmнaf^i, у e s, откуда следует, что f (x) = (KmH af)(x)                              (4.15)

для почти всех x E R n .

Равенство (4.15) означает, что f (x) E K m^ (L _p ). Теорема 2.2 доказана.

Замечание 4.1. Доказательство теоремы 2.2 существенно основано на возможности аппроксимации функции у E S по норме L _p (p >  2) функциями из Ф у , преобразования Фурье которых обращаются в нуль в некоторых окрестностях множества V . Как уже отмечалось ранее, возможность такой аппроксимации была доказана в [7] (см. также [19, гл. 2]) в случае произвольного замкнутого множества V .