Описание перехода турбулентности через скачок уплотнения на базе моделей турбулентности класса DRSM

Корректное описание усиления турбулентности при переходе через прямой скачок уплотнения на. базе уравнений Рейнольдса, (далее — SWTI — shock-wave turbulence interaction) — не решенная до сих пор задача. Существует множество примеров возникновения этого фундаментального явления: при сверхзвуковом обтекании самолета, ядерных взрывах и т.д. Конкретными примерами для практических задач аэродинамики являются недорасширенная струя и псевдоскачок в канале, в которых турбулентный поток проходит сложную ударно-волновую структуру.

Модели турбулентности, основанные на гипотезе Буссинеска, часто дают решение, зависящее от шага сетки Һ, причем коэффициент усиления может стремиться как к нулю,

«Московский физико-технический институт (национальный исследовательский университет)», 2021

так и к бесконечности при Һ ^ 0 [1]. С другой стороны, дифференциальные модели для напряжений Рейнольдса (DRSM — Differential Reynolds Stress Models) могут давать сеточнонезависимое решение [1], что и обуславливает их выбор в данной статье.

Первой полноценной DRSM-моделью турбулентности стала линейная модель Лаундера-Риса-Роди [2] 1975 г., получившая мировую известность и ставшая использоваться повсеместно в инженерных задачах. После 15 лет развития этой области, в 1991 году Специаль, Саркар и Гатский выпустили статью, в которой была предложена ставшая популярной квадратичная модель обменного члена [3]. В 1998 г. Крафт совместно с Лаундером предложили кубическую модель обменного члена [4], позволяющую корректно описать пристенную часть турбулентного пограничного слоя практически без эмпирических поправок. Все эти модели были предложены для несжимаемых течений. Однако в инженерных расчетах задач со скачками уплотнения, где проявляются сильные эффекты сжимаемости турбулентности, эти модели часто используются без дополнительной калибровки, что и влечет за собой грубые ошибки в финальных результатах. На данный момент существует работа 2019 г. [5], в которой предложена модификация моделей, устраняющая завышение кинетической энергии турбулентности на скачках уплотнения[1].Внастоящей работе этот недостаток будет исправлен через модификацию обменного члена и моделирование корреляции «давление-дивергенция скорости».

2.    Постановка задачи2.1.    Система уравнений

В работе проводится исследование поведения турбулентности при переходе через пря мой скачок уплотнения, ориентированный перпендикулярно оси х. Ищется стационар ное решение одномерных дифференциальных уравнений для напряжений Рейнольдса Ri- = n"n" [1], [6] на фоне зафиксированного среднего поля скорости, соответствующего сглаженному скачку. Ширина сглаженного скачка определяется областью, в которой мгновенный скачок совершает колебания. Уравнения для напряжений Рейнольдса, осред- ненные по Фавру [7], представляются следующим образом:

Эр R ij dt ⁺

8x_k [^pR ‘ ^{jnk p}

-К

дх ;

+ pu,' ! n - n' k + р'(n ^ 5 j _k + n " 5_ik )] =

= -p ^R;Ю; ^{+ R} jk IS   5 ⁺d'^+2p S ^- 3 ^{d +}3 ■' ^C« >• <‘>

S_____________________v_____________________/                                      S_______________v_______________/ S-----v-----''

рРц                                pHи         pW где p — плотность, n — скорость, p — коэффициент вязкости, d — дивергенция скорости,

Д- — пульсации тензора вязких напряжений, р' — пульсации давления, pPi- — производство напряжений Рейнольдса, di- — символ Кронекера, S'- — пульсации тензора скоростей деформаций, рПi- — член, отвечающий за обмен энергией между пульсациями в различных направлениях (тензор с нулевым следом), pWi- — обмен между внутренней энергией газа и энергией пульсаций (корреляция «давление-дивергенция»), Ci-(гД) — функция от средних пульсаций скорости.

2.2.    Физическая картина явления

В идеальных условиях скачок уплотнения занимает ширину порядка длины свободного пробега молекулы (примерно 10-7 м при нормальных условиях). В реальности же, скачок колеблется в пространстве под действием возмущений в набегающем потоке. Эти колебания он совершает в области, большей длины свободного пробега молекулы на несколько порядков! Значит при осреднении по времени скачок будет занимать некую конечную область (непрерывную зону сжатия). После такого осреднения поперечная и вертикальная компоненты скорости останутся нулевыми, а задача станет статистически одномерной: хоть турбулентность и является трехмерным явлением, ее статистические характеристики будут зависеть только от продольной координаты (рис. 1).

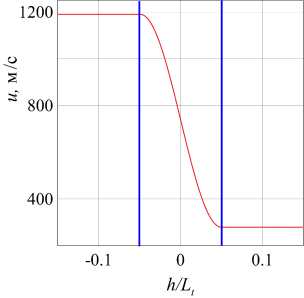
Рис. 1. Характерный профиль средней скорости в окрестности зоны сжатия. Вертикальными линиями выделена область колебаний скачка уплотнения

Задача имеет важную характерную особенность. Поток проходит область больших градиентов скорости |dгL/dx|^-1 в течение короткого времени т ~ |dй/dx|^-1^ поэтому всеми процессами, чьи масштабы времени намного больше т, можно пренебречь. Это процессы диссипации, молекулярного и турбулентного переноса.

2.3.    Упрощение системы уравнений Согласно теории RDT (rapid distortion theory - теория быстрой деформации) [8], при наложении сильных градиентов G среднего поля скорости на турбулентность, чьи масштабы времени велики по сравнению с |G-1| , все члены, не зависящие от дщ/дх^ не влияют на описание течения. Настоящая задача соответствует предположениям RDT, что позволяет существенно упростить уравнения. Геометрия градиентов в задаче следующая (рис. 1): ди, du/dx 0 0 дхз • Уравнения для тензора напряжений Рейнольдса (1) упрощаются следующим образом: dR„ ді + u _ Ж. - хх - дЯтт ді дх . дЯтт +u ■ du 2ЯххД + хх, dx — - ^Wxx • При их выводе было учтено уравнение неразрывности pt + (ри)х что позволило исключить фукнцию плотности из системы. Также, так как след обменного члена равен нулю по определению и в силу инвариантности уравнений относительно преобразования поворота вокруг продольной оси следует, что П= Пгг = Птт = — 1/2Пхх.

Сглаженный скачок занимает 5-10% от всей расчетной области в зависимости от выбранного профиля скорости. Принимается, что значения слева и справа от этой зоны соответствуют невязкому соотношению Ранкина-Гюгонио для прямого скачка [9].

На входной границе слева задается изотропная турбулентность:

2 R ij — з^1 ^з •

Индекс 1 обозначает значение слева от области, занимаемой скачком. Правая граница является свободной (используется граничное условие сноса потока).

Для замыкания обменного члена были использованы модификации полуэмпирических моделей LRR [2], SSG [3] и TCL [4], в которых тензор скоростей деформации

5 — 1 / м + диз 1

• 2 дх_з   дх г

заменен на тензор

<) = 8_гз - 1div V ^,

3 сохраняющий нулевой след в сжимаемом течении. В сделанных выше предположениях модели приобретают вид

• LRR

• SSG

_ 8 du   9С2 + 62 du

И хх ^—    -дк ⁺     ,   д-г-ка_жж,

15 dx       11   3 dx

С 2 — 0.4,

* (ru *-_■'■),, А ^{2          2}

И хх — ^С 1 dx ^R хх ^a хх ⁺ ^^С3 ^С3 V³/^2а хх з dx ^{к + С}4 з dx к<Т хх , С* — 0.9, Сз — 0.8, С3 — 0.65, С4 —0.625,

TCL

„     8 du di /2     Кхх хх — 15 ^Ж + 0.6Иж • 3°хх +--к™°хх

-

а х.) ,

где a -j — (R -j — (2к/3) d -j ) /к — тензор анизотропии напряжений Рейнольдса.

Настоящая задача в сделанных выше предположениях не имеет пространственного масштаба, поэтому все расстояния на графиках были нормированны на интегральный масштаб турбулентности L_t — к^/²/с (Lt — 1 мм). Это было сделано для удобства сравнения с данными DNS, где было принято такое же обезразмеривание.

3.    Численный метод

Решение задачи находится конечно-разностным методом. Рассматривается равномерная расчетная область с шагом сетки к. Количество узлов равно N + 1.

В качестве пространственной аппроксимации используются:

• •    для конвективных членов — upwind-схема 2 порядка аппроксимации;

• •    для Источниковых членов — центральная разность 2 порядка.

В качестве временной аппроксимации рассматривается явная одношаговая схема (метод

Эйлера) 1 порядка точности. Для шага по времени использовано конвективное условие устойчивости [10]

л к

At <----- max — i=0,N

Таким образом, конечно-разностная схема [11], [12] выглядит следующим образом:

Rxx ’ ⁿ⁺¹ — Rxx ™  _ Rxx^t — ₂ — 4Rxx T _-1 + Rxx™        _m u_i+1 — u-

+ Пхх™,

At       ⁺ " '            2k            ^{— —2Rxxi} 2k

ЛД — Ryy ™ , Ryy— — 4RyyT 1 + Ryy ™ _ 1 _m At        ^+-i             2k                  2 ^XXi .

Все значения размерных величин задаются в системе СИ.

4.    Профиль скорости

Для задания начальных условий использованы три различных профиля среднего поля скорости:

е линейное распределение и — А + Bx, и — А + B sin (Сx + О'),

• • распределение вида гиперболический тангенс

5.    Сходимость метода

п = А + В tanh (Сх + D), где А, В, С, D — константы.

Коэффициенты в профилях подобраны так, чтобы для всех профилей максимальный угол наклона графика был одинаковым (рис. 2).

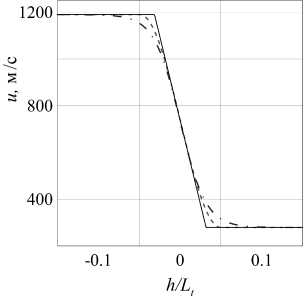
Рис. 2. Профили скорости в зоне сжатия, соответствующей скачку М = 3.5. Сплошная линия — линейный, пунктир — синус, штрихпунктир — гиперболический тангенс

На рис. 2 изображена часть расчетной области, содержащая зону непрерывного сжатия. При линейном распределении скачок занимает наименьшую область, при распределении вида гиперболический тангенс — наибольшую.

В данном разделе была исследована сходимость метода по заданному количеству точек на скачок уплотнения. Для обменного члена использовано замыкание SSG [3]. Профиль скорости внутри скачка уплотнения был взят синусоидальным.

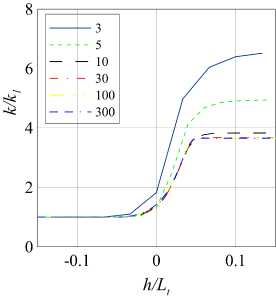
а)

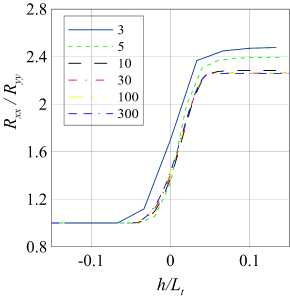
б)

Рис. 3. Распределение кинетической энергии турбулентности (а) и анизотропии турбулентности (б) в скачке. На легенде указано количество точек, выделяемых на скачок уплотнения. Режим течения (M,Mt ) = (3.5, 0.16)

На левом графике (рис. За) изображено поведение кинетической энергии турбулентности вдоль линий тока в зависимости от количества точек, выделенных на зону скачка. Как видно, при выделении на зону скачка 10 и 30 точек, расхождение в результатах минимально. Более того, графики с 30, 100 и 300 точками на зону скачка совпадают. Следовательно, при выделении на скачок более 30 точек решение перестает зависеть от густоты сетки. Аналогичную ситуацию можно наблюдать на правом графике (рис. 36), где приведены распределения анизотропии турбулентности.

6.    Независимость коэффициентов усиления Rxx и Ryy от формы профиля скорости

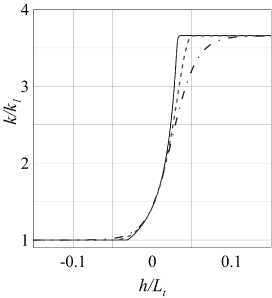
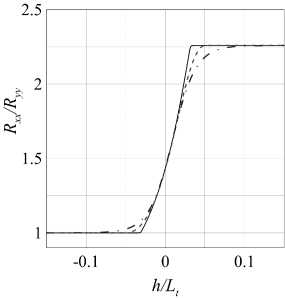
Рассмотрим некоторые характеристики турбулентности, полученные на одной сетке для разных профилей скорости (рис. 4). Для обменного члена использовано замыкание SSG. Видно, что значения, полученные за скачком, действительно не зависят от заданного профиля скорости.

а)                                                      б)

Рис. 4. Профили кинетической энергии турбулентности (а) и анизотропии пульсаций (б) вдоль линии тока. Обозначения как на рис. 2

Далее поле внутри скачка будет задаваться по синусоиде, т.к. нас интересуют лишь значения напряжений Рейнольдса за скачком уплотнения.

7.    Решение по стандартным моделям LRR, SSG, TCL

В данном разделе рассмотрим решения, полученные по стандартным моделям турбулентности, и сравним их с имеющимися экспериментальными данными [13].

В данных DNS можно наблюдать сильную немонотонность профиля кинетической энергии турбулентности и анизотропии, которые из-за ошибок аппроксимации зависят от локального профиля скачка. В настоящей задаче имеет смысл использовать значения, выходящие «на полку», так как они не зависят от формы скачка.

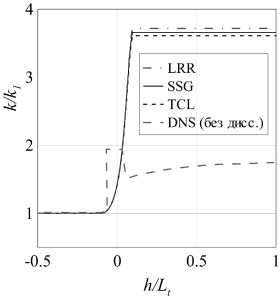
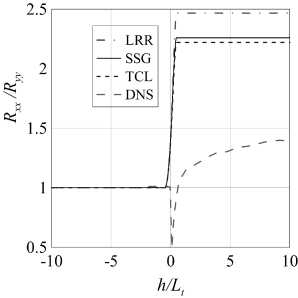
На рис. 5а изображен профиль кинетической энергии турбулентности вдоль линий тока. Как видно из графика, все стандартные модели показывают примерно один и тот же результат, который дает расхождение с данными DNS [13] (скорректированными на эффекты диссипации) более чем в 2 раза. На рис. 56 показана анизотропия турбулентности. Все модели турбулентности предсказывают усиление анизотропии в 2.2-2.5 раза, тогда как данные DNS показывают усиление в 1.4 раза. Заметим, что модель LRR, являющаяся самой простой из рассмотренных, дает наибольшую ошибку в анизотропии, тогда как модели SSG и TCL показывают практически идентичные результаты.

Посмотрим на зависимости параметров турбулентности от числа Маха скачка уплотнения.

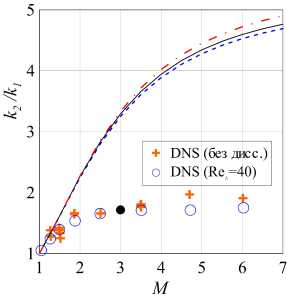
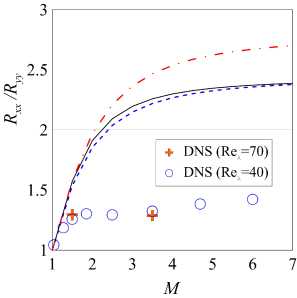
На рис. 6а изображен коэффициент усиления кинетической энергии. Видно, что все три стандартные модели дают практически идентичные результаты. Уже при числе Маха больше 1.5 можно наблюдать заметное расхождение с экспериментом, которое увеличивается по мере увеличения числа Маха. Аналогичная ситуация происходит на правом графике (рис. 66), где показан коэффициент анизотропии, посчитанный за зоной скачка в зависимости от числа Маха. Здесь также значительное расхождение с данными DNS.

Из данных эксперимента (рис. 6а) видна тенденция кинетической энергии турбулентности выходить «на полку» при числе Маха больше 3, в то время как все модели турбулентности предсказывают постоянный рост к. Для анизотропии турбулентности (рис. 66)

а)

б)

Рис. 5. Расчет по стандартным моделям кинетической энергии турбулентности (а) и анизотропии турбулентности (б) вдоль линий тока. (M,M_t ) = (3.5, 0.16)

а)

б)

Рис. 6. Расчет по стандартным моделям коэффициента усиления кинетической энергии турбулентности (а) и анизотропии турбулентности (б) при разных числах Маха скачка. Сплошная линия — SSG, пунктир — TCL, штрихпунктир — LRR. Черная точка — эксперимент Барре и др. [14]. M_t = 0.16

стандартные модели при числе Маха больше 3 дают лишь слабый дальнейший рост анизотропии.

Таким образом, модификация DRSM-моделей в задаче SWTI необходима. Следующим шагом будет выбор замыкания для обменного члена и последующая перекалибровка модели для правильного предсказания параметров турбулентности.

8.    Модификация модели

Как уже было отмечено, авторы каждой из моделей LRR [2], SSG [3] и TCL [4] не учитывали влияние дивергенции скорости на обменный член и игнорировали корреляцию «давление-дивергенция скорости». Это естественно, так как они рассматривали несжимаемое течение, а в нем дивергенция скорости равна нулю. Позже, в расчетах сжимаемых течений, традиция использовать модели без поправок на сжимаемость сохранилась. Как мы увидели в предыдущем разделе, в задаче SWTI это приводит к неприемлемым результатам расчета. Добавим в одну из рассмотренных моделей члены, зависящие от дивергенции скорости. Заметим, что тем самым мы не нарушим описание несжимаемых течений, где дивергенция скорости равна нулю.

В выражение для обменного члена следует, как минимум, добавить слагаемое, линейное относительно divV и тензора анизотропии напряжений. Из соображений размерности такое слагаемое имеет вид

^CL ^div K ^ka ij , ^CL =^const-

Заметим, что если рассмотреть уравнение для кинетической энергии турбулентности к = Rn/2,

Эй ^кахх~ДГ~, Эх

Эк Jkk Эй П_?? / , 2 ₇ \ Эй 2 ₇ Эй л + ^й"?Т = ^—Rxxy; + = ^— ( ^кахх + д^к I = ^— о^куг" Эх Эх Эх 2 \ 3 ) Эх 3 Эх

-

≡0

то станет видно: из-за того, что обменный член является тензором с нулевым следом, вне- сение предложенного выше слагаемого не повлияет напрямую на описание средней кинетической энергии турбулентности.

Далее, в сжимаемых течениях след выражения 2p‘S‘j = 2p‘d’’ не равен нулю. Следовательно, в общем случае нужно учесть влияние p^fdⁿ. В отличие от Пгд этот член попадает в уравнение для кинетической энергии турбулентности и может напрямую влиять на коэффициент усиления к на скачке.

8.1.    Корреляция «давление-дивергенция»

Будем моделировать p’d’’/р на основании теории размерности. Размерность этого выражения равна м² / с³. Значит, модель следует составить из инвариантов определяющих величин, дающих правильную размерность. Выберем инварианты R ^j , имеющего размерность м² / с² и Эй_г /Эх ^ — с^-1. Если ограничиться линейными инвариантами R^ = 2к и divV = dn/dx, то единственной возможной замыкающей моделью будет выражение ^dй

^C pd ^k j , ^C pd — Const. dx

При калибровке констант будем использовать модель обменного члена SSG [3]. Этот выбор обусловлен ее популярностью в инженерных расчетах.

Система уравнений, требующая калибровки, окончательно принимает следующий вид:

ЭR xx Эі

_ ЭR u "

-

ЭRTT   ~ ЭRTT

--+ й——

dй            du

2Rxx—1  + хх + ^pdk^~, dx            dx

= — 1П

dй ^{+ C} pd^k~j~, dx

П

хх

0 9 -R a ^и ‘^ ₇ -^хх ^а хх dx

+ ^0.8 — О.ббДзДа хх) •

2 dй 7   _      2dй, к + 0.625 • - —кахх

3 dx          3 dx

⁺ c du^

dй 7

Д ^ка хх . dx

8.2.    Калибровка модели

Константы Cd^ и C_p d будем калибровать на одном режиме с числом Маха, равным 3.5, и турбулентным числом Маха 0.16. Ожидается, что константа C_p d в основном будет влиять на усиление кинетической энергии турбулентности, а константа Cd^ — на анизотропию напряжений Рейнольдса за скачком уплотнения.

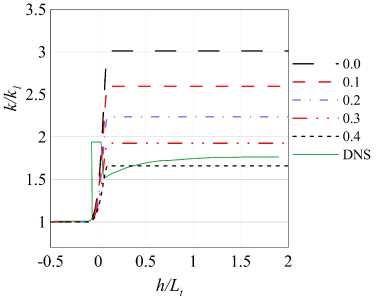
Рис. 7. Профили кинетической энергии турбулентности для различных С _ра. Во всех расчетах задано С^ = 4.9. (M,M_t ) = (3.5,0.16)

Согласно экспериментальным данным [13], на данном режиме усиление кинетической энергии турбулентности к₂/к 1 равно 1.77, а значение анизотропии напряжений R_xx/R_yy за скачком уплотнения составляет 1.35.

Посмотрев на рис. 7, можно увидеть, что, как и ожидалось, константа С_ра сильно влияет на величину кинетической энергии турбулентности за скачком. Это позволяет легко добиться корректного значения к₂/к 1 по модифицированной модели.

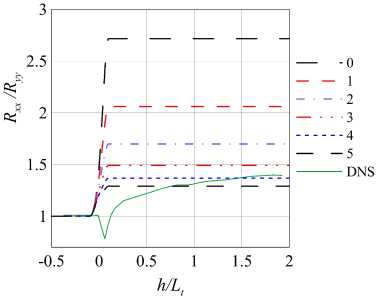
Рис. 8. Профили анизотропии турбулентности для различных С^ . Во всех расчетах задано C_pd = 0.4. (M,Mt ) = (3.5,0.16)

На рис. 8 изображено поведение анизотропии турбулентности вдоль линий тока при различных С"^. Мы видим прямое влияние этого коэффициента на значение анизотропии. Обменный член отвечает за перераспределение энергии между напряжениями Рейнольдса, а именно, в нем присутствует константа С^.

В результате калибровки методом покоординатного спуска [15] для модели SSG были получены следующие значения констант:

Ск = 4.9, С_ра = 0.4.

Погрешность в предсказании коэффициента усиления кинетической энергии турбулентности составила менее 10%, а в предсказании анизотропии — менее 5%.

8.3.    Результаты расчета по модифицированной модели

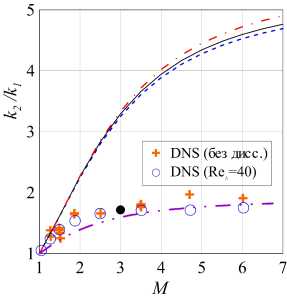
Сравним решения, полученные для стандартных моделей и модифицированной модели SSG при различных числах Маха скачка (рис. 9).

а)

б)

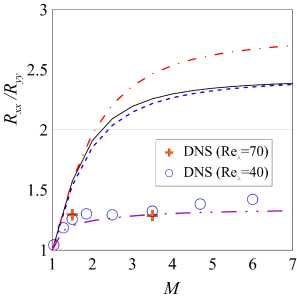
Рис. 9. Расчет по модифицированной модели SSG коэффициента усиления кинетической энергии турбулентности (а) и анизотропии турбулентности (б) при разных числах Маха скачка. Сплошная линия — SSG, пунктир — TCL, штрихпунктир — LRR, штрихпунктир с двумя точками — модифицированная модель. Черная точка — эксперимент Барре и др. [14]. M_t = 0.16

На левом графике (рис. 9а) показан коэффициент усиления кинетической энергии турбулентности как функция от числа Маха. Новая модель аппроксимирует эксперимент с погрешностью до 10% для всего диапазона значений М. На рис. 96 изображена анизотропия турбулентности в зависимости от числа Маха, которая приближает численные данные с погрешностью меньше 10%, однако при числе Маха больше 5 ошибка моделирования становится около 10%.

Данные результаты можно признать существенным уточнением модели SSG. Заметим, что калибровка проводилась только на одном режиме с числом Маха 3.5, однако этого хватило для согласования с данными DNS для всего диапазона М с точностью 10%.

9.    Заключение

Настоящая работа позволяет сделать следующие выводы:

• 1)    Стандартные DRSM-модели (LRR, SSG, TCL) завышают усиление кинетической энергии турбулентности на скачках с М >  2 как минимум в 2 раза, анизотропии — более чем в 2 раза.

• 2)    Учет дивергенции скорости в обменном члене и корреляции «давление-дивергенция» позволяет достичь согласования с DNS с точностью 10%.

• 3)    При расчетах течений со скачками уплотнения недостаточное (5 и менее ячеек) разрешение зоны скачка может приводить к перепроизводству кинетической энергии турбулентности.

Автор выражает благодарность своему научному руководителю Трошину А. И. за помощь при создании настоящей работы.