Описание вязкоупругих свойств низко- и высоконаполненных эластомерных нанокомпозитов

Свойства вязкоупругих материалов определяются упругим (равновесным) откликом среды и временными (неравновесными) процессами, проходящими в них. Кроме того, в сложный характер поведения эластомерных материалов вносят вклад остаточные деформации, гистерезисные потери и размягчение Маллинза после первого цикла нагружения. Известно, что степень проявления данных явлений зависит не только от скорости приложения нагрузки, но и от структуры материала, а также от величины заданных деформаций среды. Исторически выделяют два подхода для описания поведения эластомерных материалов – на основе термодинамики сплошных сред [2-5] и на основе идей микромеханики [6, 7]. В полимерах свойства во многом определяются их строением, но идеи рассматривать материал как сплошную среду находят существенно больший отклик, благодаря простоте построения моделей и универсальности их применения.

Рассмотрение случая одноосного растяжения с постоянной скоростью

В работе [8] была описана новая термодинамическая модель поведения вязкоупругих материалов в условиях конечных деформаций, в рамках которой тензор напряжений Коши представляется виде суммы равновесного и диссипативного слагаемых:

T = T eq + T dis .

Также в работе [8] получено уравнение эволюции тензора А , отвечающего за неупругие (зависящие от скоростей деформаций) растяжения среды:

А + 1А —bU,          (1)

т где b и 1/т - неотрицательные функции параметров состояния среды; U - тензор скоростей растяжений среды.

Рассмотрим уравнение эволюции (1) в случае одноосного нагружения материала с

постоянной скоростью. В момент времени t * переменные величины принимают значения Л * и a* ( i = 1, 2, 3 ). На интервале времени от t * до t кратности удлинений меняются следующим образом: Л 1 = Л, Л₂ — Л₃ — 1/VA , где Л = Л * + AAt , Л = const , At = t — t* . Также имеем: At = 1 (Л — Л * ) , a, = ^-Л.

Л                ОЛ

Рассмотрим случай i = 1. Необходимо найти решение уравнения a1 + - a1 — ЬЛ ° —1 +—aa1 — b    (2)

т           оЛ тЛ

при условии a1 — a * при Л — Л * .

Общее решение уравнения (2) имеет вид a₁(Л) — С exp [— ^л] + ЬЛт, где С - произвольная постоянная.

Решение с учетом условия a1 — a * при

Л — Л * принимает вид a₁(A) —

— (a* — ЬЛт) exp [р (Л * — Л)] + ЬЛт. ^ Отметим, что a 1 (A) ^ ЬЛт при Л ^ +^ .

Формула (3) при условии Л — 0 принимает вид

a 1 (A) — a* exp

—

1 - At , т

откуда видно, что величину т можно трактовать как время релаксации материала.

Теперь рассмотрим случай i — 2 , i — 3 .

Необходимо найти решение уравнения

1        ЬЛ a2,3 +Ta2,3 —--3 °

‘           2Л 2

da₂,3 .    1           ЬЛ

“0f ^{A +} 7^a^3 ^{— —}—з^.

Найдем решение уравнения (4) в виде

a 2,3 ⁽ A) — a^exp

— зр ⁽Л — Л * )

+

+ exp

—ьЛ|^(Л)

при условии ^(Л * ) — 0 .

: (4)

Тогда уравнение (4) принимает вид

^exp[—К^Л ]

3^(Л) ° ЗЛ ^—

W). _ 1ГЛ —

—

л

ь

—з exp 2Л 2

ьЛ

2Л 2 [Й”

° ^(Л) = — 2 f

Tuexpv

1 ьЧ d^

Рассмотрим для ф(Л) :

л *

отдельно интеграл в выражении

Л /■НкФ^{? —} Л * S ^z

Л/Лт

fT ^—u     1   ^Л/'

^— f — иЛт ^—      f

I dS — Лтdu     ^Лт Л , /Лт

е ^и

U 3/2 ^{du —}

Лт

+rn

f

1 Л * ^{и 2}

\ Лт

+^

и

—

f ^du

Л  U 2

Лт

разными наполнителями. Ранее данный вид механических испытаний использовался для анализа механических свойств полиуретановых материалов [9].

Сущность эксперимента: образец сначала растягивают до максимальной заданной деформации, выдерживают при этой деформации заданное время, сжимают до исходного ненагруженного состояния, выдерживают заданное время, затем циклически деформируют с выдержкой во времени на каждой ступени деформации при растяжении и сжатии, при этом деформация на каждом цикле растяжения задается меньшей, чем на предыдущем цикле, а деформация на каждом цикле разгрузки задается большей, чем на предыдущем цикле. Более подробно предложенная программа испытаний рассмотрена в [5, 9, 10].

В табл. 1 и 2 указана информация об алгоритме деформирования образцов.

₌ 1 ^3/2 (—

ТЛГ (л*А

/

Л * /Лт)  Е 3/2 (—Л/Лт)\

1/2      Гт /й_>¹/2   ) ^—

(Л/Лт)

_ ^Е3/2 ^(—Л * ^/Лт)

—

^Л *

^Е 3/2 ^(—Л/Лт)

,

' Л

где En(z) = J+ ^-dt - интегральная экспо нента порядка п.

В итоге, для случая i — 2 и i — 3 получаем решение:

* ¹

^а 2,3 ^(Л) — ^а2,3 ^ex p [ ^—^^{(Л — Л , )}

—

— ^Ь ехР

1 J

—кт

^ Е 3/2С

_•

_•

:—Л * /Лт)   Ез/2(—Л/Лт)

—

Л *

ТЛ

■)

Отметим, что а₂ , ₃(Л) ^ 0 при Л ^ +« .

Сравнение теоретических и экспериментальных кривых нагружения

Для проведения сравнения теоретических результатов, полученных в рамках новой термодинамической модели, с экспериментальными данными были проведены одноосные испытания с вложенными циклами нагружения для образцов низко- и высокона-полненных эластомерных нанокомпозитов с

Таблица 1. Информация об алгоритме деформирования образца с 7 массовыми частями наполнителя в одноосном испытании с вложенными циклами

	Предельное значение кратности удлинения	Скорость деформирования	Продолжительность остановки захватов в конце цикла
1. Нагружение образца	max Л = 2	• Л = 1 мин-1	20 мин
Разгрузка	min Л = 1	Л = -1 мин-1	20 мин
2. Нагружение образца	max Л = 2	• Л = 1 мин-1	10 мин
Разгрузка	min Л = 1.2	Л = -0.5 мин-1	10 мин
3. Нагружение образца	max Л = 1.9	Л = 0.5 мин-1	10 мин
Разгрузка	min Л = 1.3	Л = -0.2 мин-1	10 мин
4. Нагружение образца	max Л = 1.8	Л = 0.2 мин-1	10 мин
Разгрузка	min Л = 1.4	Л = -0.05 мин-1	10 мин
5. Нагружение образца	max Л = 1.7	Л = 0.05 мин-1	10 мин
Разгрузка	min Л = 1.5	Л = -0.05 мин-1	10 мин
6. Нагружение образца	max Л = 1.6	Л = 0.05 мин-1	10 мин
Разгрузка	min Л = 1	Л = -0.05 мин-1	Завершение эксперимента

Таблица 2. Информация об алгоритме деформирования образца с 50 массовыми частями наполнителя в одноосном испытании с вложенными циклами

	Предельное значение кратности удлинения	Скорость деформирования	Продолжительность остановки захватов в конце цикла
1. Нагружение образца	max A = 2	Л = 4 мин-1	20 мин
Разгрузка	min A = 1.1	Л = -4 мин-1	20 мин
2. Нагружение образца	max A = 1.9	Л = 4 мин-1	10 мин
Разгрузка	min A = 1.2	Л = -4 мин-1	10 мин
3. Нагружение образца	max A = 1.8	Л = 1 мин-1	10 мин
Разгрузка	min A = 1.3	Л = -1 мин-1	10 мин
4. Нагружение образца	max A = 1.7	Л = 0.25 мин-1	10 мин
Разгрузка	min A = 1.4	Л = -0.25 мин-1	Завершение эксперимента

Для расчета равновесной части тензора напряжений Коши использовался потенциал упругой энергии, описанный в работах [9, 10]:

ш = a C ln(/ 1 ) + С ln (1 — -1) + const, 1*

где 11 = A1 + A2 + A2 ; a , C , I_t - материальные константы.

При этом считается, что материал несжимаем: A 1 A₂A₃ = 1 .

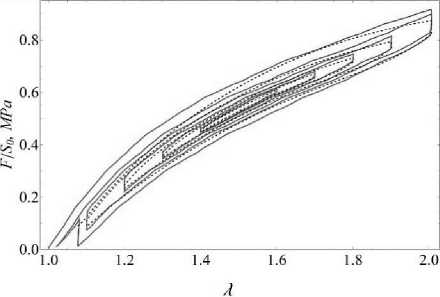
Рис. 1. График экспериментальных данных (сплошная линия) и теоретической кривой (пунктирная линия) для нанокомпозита с 7 массовыми частями наполнителя (детонационные наноалмазы)

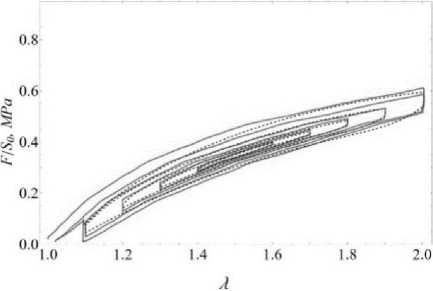
Рис. 2. График экспериментальных данных (сплошная линия) и теоретической кривой (пунктирная линия) для нанокомпозита с 7 массовыми частями наполнителя (графен)

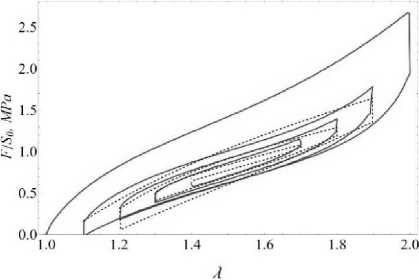
Рис. 3. График экспериментальных данных (сплошная линия) и теоретической кривой (пунктирная линия) для нанокомпозита с 50 массовыми частями наполнителя (графен)

При такой форме записи упругого потенциала равновесная часть напряжений при- нимает вид:

eq

^O 1

■■■           .                +

В соответствии с формулой (3) диссипативная часть напряжений имеет вид: ^оЛ . ^оЛ^_;^ехр|  ‘^  .:,: .^.

В итоге единственная ненулевая компонента напряжений O1, соответствующая истинным напряжениям в образце, определяется суммой найденных равновесной и диссипативной частей:

O1 = ol^q + O'!¹¹⁵.

На рис. 1–3 представлены результаты расчетов, полученные согласно предложенной модели. Рассмотренные материалы представляли собой нанокомпозиты на основе бутади- ен-стирольной матрицы с 7 или 50 массовыми частями наполнителя (детонационные наноалмазы или графеновые пластины). Обозначения на рисунках: F - действующая сила, S0 -начальное сечение образца.

Отметим, что при построении теоретической кривой не рассматривался первый цикл нагружения. Анализ характера поведения композитов проводился на втором и последующих циклах, то есть были построены кривые вязкоупругих свойств уже размягченных материалов.

В дальнейшем планируется учесть эффект размягчения Маллинза в расчетах.

Уникальность предложенной модели заключается в найденном аналитическом решении для диссипативной части тензора напряжений в случае одноосного нагружения при постоянной скорости деформирования. И в отличие от других вязкоупругих моделей это дает возможность с легкостью анализировать получаемые экспериментальные данные.

Работа выполнена при поддержке РФФИ (грант №. 19-08-00725) и в рамках госбюджетной темы (рег. номер АААА-А20-120022590044-7).