Определение частоты колебаний нелинейной системы с одной степенью свободы методом линеаризации

Предложена новая схема определения частоты колебаний для нелинейной системы с одной степенью свободы методом линеаризации. Вычисление частоты колебаний по этой схеме превосходит по точности все другие известные способы ее вычисления.

• 1.    В связи с отсутствием точных методов решения нелинейных дифференциальных уравнений вида

-+f (x)=0, где f (—x) = — f (x) , представляет большой практический интерес определение частоты колебаний м = к уравнения (1) при помощи приближенных методов. Одним из таких приближенных методов является метод линеаризации уравнения (1), в котором делают замену

f (x) = к2 x .

Тогда уравнение (1) становится линейным

dx + к2 x = 0 , dt2

которое при начальных условиях

t = 0, x (0) = A, — = 0 dt имеет простое решение

x(t) = A cos kt с неизвестной постоянной частотой k .

Из выражения (2) следует, что размерность [ к 2 ] = [ f ( x ) / x ] = c

— 2

.

Поэтому, если равенство (2) поделить на квадрат частоты to 2 = 1 c 2, k2    f(x)/x то величины 2 ,       2    окажутся безразмерными, которые во

ωω всем дальнейшем тексте статьи будем обозначать в виде k2 и f(x)/x соответственно, где k2 является угловым коэффициентом прямой у = к x .

вычисления

Многие авторы предложили свои формулы для величины k ² . Рассмотрим некоторые из них.

2 f(A)

.

• 1)    Формула Куликова Н.К. [1]: к =------

• 2)    Формула Пановко Я.Г. [2, 3 стр. 68]:

• 2    5A3к = —- x3f(x)^x .

A 0

• 3)    Формула Цыпкина Я.З. [4]:

• к = — [f (A/2) + f (A)].3A

• 2.    Схема вычисления величины k ² для уравнения (1).

Формула Цыпкина Я.З. (8) является более точной, чем все остальные вышеуказанные.

В данной работе предложена схема расчета квадрата частоты ω ² k ² ( to ² = 1 c 2 ) , см. замечание в п. 1, для уравнения (1), которая позволяет вычислить это значение в 6 раз точнее, чем по формуле Цыпкина Я.З. (8).

• 1)    Изобразим графически функцию f ( x ) на отрезке [0, A ] .

Функция J = f (x) изображена на рис. 1 кривой MLN. Разобьем отрезок [0, A] на две равные части, как показано на рисунке. Точки M , L , N соединим последовательными хордами, длины которых равны l1 = ML и l2 = LN .

Вычислим угловые коэффициенты этих хорд и их длины. к _о2, =_№= f ( A /J) ; ^{f (0)} = A[ f ( A /2) - f (0)] ,

A/2     A k« = tga2 = AV f (A) - f(A /2)].(10)

Вычислим длины хорд ML и LN .

11 = ML = V[f (A /2) - f (0)]2 + (A /2)2 ,(11)

12 = LN = V[f (A) - f (A /2)]2 + (A /2)2 .(12)

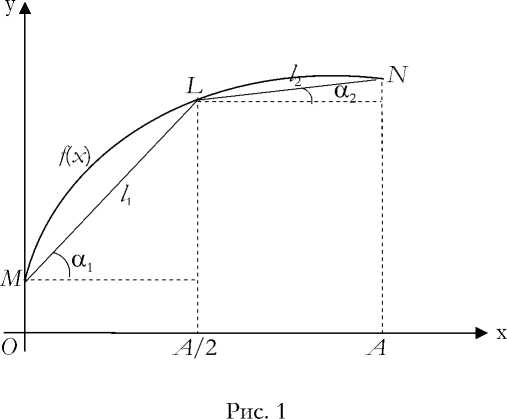
Сумма длин этих хорд равна 1 = 1 1 + 1 ₂ .

Угловые коэффициенты k 01 и k 02 возьмем в долях 1 1 / 1 и 1 ₂ / 1

соответственно:

1 2 _ / 2 ¹ 1      / 2 _ / 2 ¹ 2

k — k , k — k_m .

1       01 1 a 2       02

Их среднее значение равно k? x = k ² + k ² ,

где k X 2 обозначает, что вычисление k ² произведено методом хорд.

• 2)    Вычислим теперь значение k ² методом касательной, рис. 2.

  

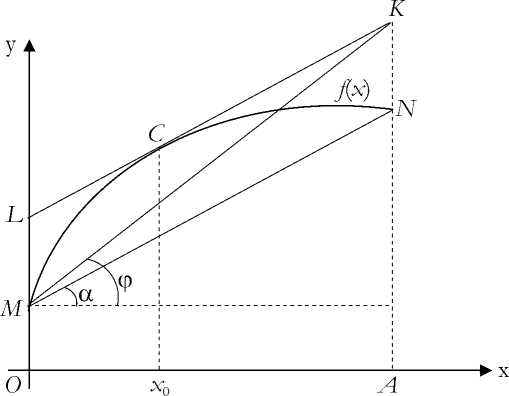
  Рис. 2

  
  

Угловой коэффициент хорды MN равен

k

MN

= tga = f(A) - f(0) A

Угловой коэффициент касательной LK равен

² k LK

df(x) dx

Потребуем, чтобы MN // LK , тогда должно

выполняться

равенство

k LK = k MN •

Подставив в это условие выражения (15) и (16), получим

df (x) = f (A) - f (0)

dx         A .

Разрешив это       уравнение,       найдем точку

C(x0, jy0), x = x0, jy = y0 = f (x0), в которой касательная

LK касается кривой jy = f (x) .

Запишем уравнение этой касательной, проходящей через точку

C(x0, y0):

y — у 0 = k Lк ( x — x 0 ) , где угловой коэффициент касательной LK равен 2 df ( x 0) kLK       ,     • dx Из (19) выразим j ( x ) и вычислим j ( A ) = AK .

(19) (20) (21)

Фигура MLKN на рис. 2 является параллелограммом с диагональю MK . Определим ее угловой коэффициент kk = kM K

= ^ф =

AK — OM = y(A) - f (0)

AA

где y ( A ) взято из равенства (21).

• 3)    Среднее значение k ² находим из выражений (14) и (22)

• 3.    Сравнение разных формул для вычисления k ² на примере

1k- = -(kx + k-) .                                   (23)

математического маятника.

• 1)    Уравнение колебаний математического маятника имеет вид

d 2φ g

—у + — sin ф = 0, dt2 l где φ – угол отклонения нити маятника от его положения равновесия (ф = 0), l — длина нити маятника, g — ускорение свободного падения.

Решение уравнения (24) не выражается через элементарные функции. Обозначим через to 0 = ^ g /l круговую частоту колебаний маятника для случая sin ф ~ ф .

Точное значение периода колебаний математического маятника выражается по форм уле [5, стр. 121]:

T = 4 XXк = 4 K / to 0 ,                      (25)

π /2        _dθ

где K = I .

0 V1 — m2 sin2 6

полный эллиптический интеграл первого рода, m = sin(a /2) — модуль этого эллиптического интеграла,

α – амплитуда колебаний маятника.

2π

Частота колебаний маятника to =--

T

πω ₀

₂    , а ее квадрат равен

ω

^nto о

12 к;

• 2)    Рассмотрим математический маятник, уравнение колебаний

которого имеет вид d2x

—— + sin x = 0 , dt

2 и -2

откуда следует, что to ₀ = 1 С . В этом случае квадрат частоты его колебаний согласно выражению (27) и замечанию в п. 1 запишется в виде

to2 = to 2 k2 = (п /2 K )2.                                 (29)

Для уравнения (28) возьмем начальные условия

t = 0, x (0) = A = -, — = 0.                 (30)2 dt

При x(0) = A = а = п /2 модуль m эллиптического интеграла (26) равен m = sin(а /2) = sin(п /4) = V2 / 2, mг = 0,5.

Для m ² = 0,5 значение интеграла (26) находим по таблице [6, стр.

288]:

к = 1,85407.

По формуле (29) вычисляем точное значение квадрата частоты to 0 k •

(         '

( 2 • 1,85407 )

= 0,7178 c2 ,

где to 2 = 1 С ² , а величина k • = 0,7178 является точным значением углового коэффициента прямой _y = k ² x в соответствии со сделанным замечанием в п. 1.

Вычислим теперь значение k ² по приведенным выше формулам и по нашей схеме для математического маятника, описываемого уравнением (28) при начальных условиях (30).

Нелинейная часть уравнения (28) f ( x ) = sin x .

Для расчетов примем п = 3,1416 .

• а)    Формула Куликова Н.К. (6):

2 f ( A )   sin( π /2)

к =-----=--------= 0,6366 .

A π /2

Абсолютная ее погрешность равна

Д = к• — к2 = 0,7178 - 0,6366 = 0,0812 , относительная погрешность

Δ        0 0812

б = и . 100% = _,-- 100% = 11,3% .

к 2          0,7178

• б)    Формула Пановко Я.Г. (7):

5 ^A

A 5 3

x ( x

— x ³ / 6) dx =

к² = —- J x³ f ( x)d:

A 0

= 1 —

5 A ²

= 1 —

5 • п

42 • 4

= 0,7063.

Здесь мы приняли, что sin x ~ x — x 3 /6 .

Абсолютная погрешность Д = 0,7178 — 0,7063 = 0,0115, относительная погрешность

0,0115

0,7178

• 100% = 1,60%

• в)    Формула Цыпкина Я.З. (8):

к 2 = Л[ f ( A /2) ⁺ f ( A )] = тЛ%^п 7 ⁺ sin 7 ] = 0,7245 •

3 A                  3 • п /2   4     2

Абсолютная погрешность Д = 0,7178 — 0,7245 = —0,0067, относительная погрешность б = —----• 100% = 0,93% .

0,7178

• г)    Наша схема вычисления k ² .

Используя формулы! (9) - (14) и f ( x ) = sin x , A = п / 2 , п = 3,1416 , последовательно вычисляем: к ² = si^{n( п} /4) ^— siⁿ⁰ = 0,9003,

⁰¹ π /4

2 si ^{n( п} /2) ^{— sin( n} /4) k_m =--------------------= 0,3 729 ,

⁰²            π /4

1 1 =

l 2

Г ■ ⁿ sin- l 4

Г n sin — l 2

A ² sin0

J

+

. n sin —

4 J

+

2 n l4 J l4J

= 4,2273,

= 3,3529 , l = 1 1 + 1 ₂ = 7,5802 ,

k 2 = k 2 1 = 0,5021, 1        01 l kX = k 12 + k 22 = 0,6670

.

k 2 = k ² l ² = 0,1649, 2       02 _l

Вычисляем k ² методом касательной, используя формулы (15) – (22):

MN

^{sin( n /2) — sin0 2} --------------= — = 0,6366 ,

₂ d (sin x )

k, ^ =--------= cos x ,

LK dx

π/2 π kмм = k2K ^ cosx = 0,6366 ^ x = xn = 50o28' = 0,8808 , MN LK                            0

y0 = sinx0 = sin50o28' = 0,7713 , уравнение касательной LK :

j — у ₀ = k L_K ( x — x ₀) ^ y ( x ) = 0,6366 x + 0,2106 ,

y ( A ) = y ( n /2) = AK = 0,6366 • ( n /2) + 0,2106 = 1.2106 ,

, ₂ ,₂           1,2106 — 0 „ „

^k k = ^k MK = ^t gф =---- 77-- = ^0,7707 •

π /2

Из (33) и (34) находим k2 = 2(kX + k2) = 2(0,6670 + 0,7707) = 0,7189 .

Абсолютная погрешность

Д = k 2 — k ² = 0,7178 — 0,7189 = — 0,0011,

0,0011

относительная погрешность 8 =------• 100% = 0,15% .

0,7178

Наше значение k2 = 0,7189 , 8 = 0,15% в 6 раз точнее, чем по формуле Цыпкина Я.З. : k2 = 0,7245 , 8 = 0,93% .

Точное значение k 2 = 0,7178 .

Описанная выше схема определения k ² основывалась на возрастающей функции f ( x ) . Аналогичным образом можно вычислить k ² и для убывающей функции.

Результаты вычислений k2 ' для f (x) = sin x , A = n / 2 и k 2 = 0,7178 сведем в таблицу.

Автор	Формула	k 2	A = k 2 - k2	8 = A . 100% k 2
Куликов, [1]	(6)	0,6366	0,0812	11,3%
Пановко, [2,3]	(7)	0,7063	0,0115	1,60%
Цыпкин, [4]	(8)	0,7245	– 0,0067	0,93%
Недосекин, [эта статья]		0,7189	– 0,0011	0,15%