Определение давления, нагрузки и сжимающих напряжений для сферического эндопротеза тазобедренного сустава человека

В статье представлен численный анализ давления, нагружения и сжимающих напряжений, возникающих в сферическом эндопротезе тазобедренного сустава человека.

Приведем вопросы, освещенные в представленных публикациях. Arfoke et al. описали контактное давление в тазобедренном суставе человека [1]. B^dzinski отразил избранные вопросы инженерной биомеханики и биотрибологии [2]. Автор смоделировал давление в тазобедренном суставе человека с эллиптической и сферической головкой бедра при симметричном стационарном течении синовиальной жидкости [3, 4]. Также он описал распределение давления, нагрузку и сжимающие напряжения не только для сферического тазобедренного сустава [5, 6], но также для эллиптического тазобедренного сустава и его эндопротеза, используя несимметричную стационарную модель течения синовиальной жидкости [7-9]. Dowson описал основные проблемы биотрибологии, ортопедических имплантатов и биоматериалов [10-12]. Dumbleton отразил избранные проблемы трибологии естественного и искусственного суставов [13]. Eisenhart et al. получили распределение давления во время моделируемой ходьбы и толщины хряща тазобедренного сустава человека [14]. Ferguson et al.

показали влияние вертлужной впадины на консолидацию суставного хряща [15]. Firkins et al. представили новый вариант керамико-металлического протеза тазобедренного сустава с малым износом [16]. Grenda et al. описали контактное давление в нормальном суставе во время стояния на одной ноге и исследовали влияние половых и анатомических параметров [17]. Hlavacek et al. описали влияние несовпадения суставных поверхностей на касательное (вызванное недостаточной смазкой) и контактное давление в нагруженных суставах [18]. Huiskes et al. представили биомеханику искусственного тазобедренного сустава [19]. Jalali-Vahid et al. спрогнозировали толщину смазочного слоя в тазобедренном суставе [20]. Kusz et al. представили сравнительную оценку погрешности вычисления напряжений в математических моделях естественного тазобедренного сустава и сустава после установки протеза Parhofer-Monch [21]. Van Mow et al. описали биомеханику искусственных суставов и роль смазки в биомеханических суставах [22]. Ozkaya et al. описали поведение суставов с позиции фундаментальных законов биомеханики [23]. Rushfeld et al. рассмотрели влияние формы суставного хряща на распределение давления в тазобедренном суставе [24]. Ryniewicz в рамках диссертационной работы проводит анализ механизма трения в тазобедренном суставе человека [25]. Udofia et al. проанализировали упругогидродинамическое смазывание в протезах типа металл-металл [26]. Wierzcholski представил трибологию суставов человека [27], теорию гидродинамческой смазки зазора тазобедренного сустава [28, 29], определил несущие нагрузки для несимметричного потока синовиальной жидкости в тазобедренном суставе с переменной суставным зазором [30, 31] и вычислил давление, нагрузку и сжимающие напряжения для несимметричной стационарной смазки тазобедренного сустава [32, 33]. Также Wierzcholski впервые описал смазывающий поток синовиальной жидкости тазобедренного сустава, используя несимметричную нестационарную модель течения жидкости [30, 31].

Нагрузка, сжимающие напряжения и давление для переменной суставной щели при несимметричном течении синовиальной жидкости для сферических эндопротезов тазобедренного сустава не были изучены ранее.

Новыми результатами данной работы в сравнении с вышеназванными публикациями являются описания давления, нагрузки и сжимающих напряжений, вычисленные для сферического эндопротеза тазобедренного сустава человека с использованием модели несимметричного нестационарного течения жидкости.

Знание указанных рабочих параметров сферического эндопротеза тазобедренного сустава человека может быть полезно в ортопедической диагностике и клинической практике.

Механическая и математическая модель

В работе рассматривается нестационарное изотермическое несимметричное течение несжимаемой синовиальной жидкости с неньютоновскими свойствами. Поток синовиальной жидкости вызван вращательным движением сферической головки эндопротеза. В модели рассматриваются переменный суставной зазор, переменная вязкость и постоянная плотность синовиальной жидкости. Шероховатость и нерегулярность поверхностей эндопротеза считаются незначительными и не рассматриваются.

Расчеты проводятся в сферической системе координат ( ϕ , r , ξ ) , где ϕ – окружное направление, r – радиальное направление (высота зазора протеза) и ξ –

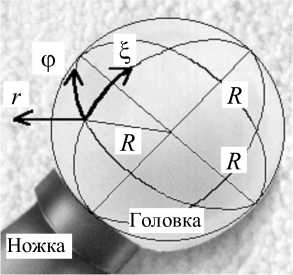
Рис. 1. Сферическая система координат ( ф , r , 5 ) на головке эндопротеза

Рис. 2б. Ножка и головка сферического эндопротеза

Рис. 2а.

Общий вид сферического эндопротеза

Рис. 2в. Детали сферического эндопротеза

меридиональное направление (рис. 1). Произвольные вращающиеся поверхности создают зазор сферического искусственного сустава, где находится синовиальная жидкость. Типичный экземпляр сферического блочного эндопротеза показан ( FRANKOBAL ^TM) на рис. 2а-в.

Выведем упрощенные основные уравнения, описывающие поток в некотором зазоре протеза. Пренебрегая слагаемыми порядка Re Т и Т = е / a « 10 -4 , а также центробежными силами, система уравнений сохранения количества движения и уравнение неразрывности для несжимаемой синовиальной жидкости в сферической системе координат с учетом упрощений для пограничного слоя принимают вид [27-35]:

R

cosec

5) дp д — I —+— пRJJд— дr

V

p

д V) д r J

,

д V

о = 5 Р , д r

о=-^+ д п д5 д r

V

д V )

■ p

д r J

,

5р Vr

д

—^- + R sin — —- + R— V sin д5 ⁵

дф

R J д r

= 0,

где 0 < — <  2 п , 0 <  r < е , b m < 5, <  b s , символы b m , b s означают пределы слоя смазки. Символы V _— , V_r, V = и p являются неизвестными функциями в упрощенных уравнениях (1) - (4), где R - радиус сферической головки эндопротеза.

Поток синовиальной жидкости порождается вращением головки протеза, но протезная чаша остается неподвижной. Граничные условия для скорости течения жидкости принимают вид [27-35]:

• •    для сферической головки эндопротеза:

  Г _ф = to R sin

  
  

  R J

  
  

  V_r = 0, V ₅= о при r = 0 .

  
  
  
  

• •    для сферической протезной чаши:

• V — = 0, V r = 0, V § = 0 при r = е ( ф , 5 ),

  
  
  

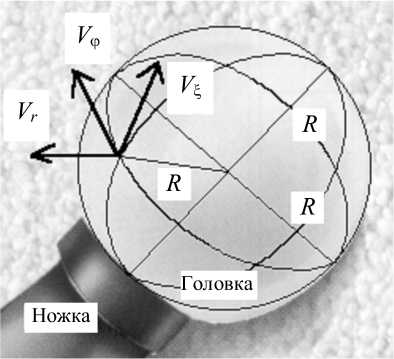
  Рис. 3. Компоненты вектора скорости течения синовиальной жидкости V _Ф , V r , V ^

  
  
  

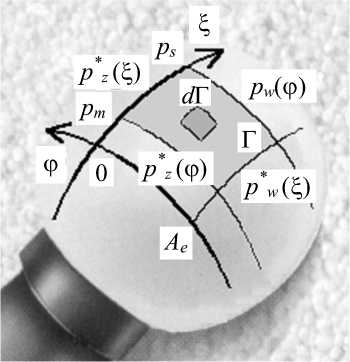
  Рис. 4. Граничные условия для напряжений

  
  

где r = г ( ф , ^ ) означает высоту зазора между двумя искусственными поверхностями.

Распределенное давление противодействует несущей нагрузке эндопротеза. На входе в искусственный зазор давление равно давлению среды, но внутри зазора давление равно внутреннему давлению. Таким образом, граничные условия для напряжений принимают вид [27-35]:

Pz ⁽ Ф ) = Р ( ф , ^ = b m ) ^, P z ( 5 ) = Р ( ф = ⁰, ^ ) ^{, (7)}

P w ⁽ Ф ) = Р ( Ф ^, ^ = ^bs ) ^, P W ( 5 ) = Р ( ф = ^Ae ^, ^ ) ^{, (8)} где p_z ( ф ), р * ( ^ ) - напряжение на входе в зазор в направлениях ф и £ , соответственно, p w ( ф ), P W ( 5 ) — напряжение на выходе из зазора в направлениях ф и £ , соответственно.

Направление компонент вектора скорости течения синовиальной жидкости показано на рис. 3, схема граничных условий для напряжений дана на рис. 4.

С учетом указанных граничных условий получим из уравнений (1) и (3) компоненты скорости течения синовиальной жидкости V _ф , V ; в направлениях ф и £ , соответственно. Подставим решения для V ϕ и V ξ в уравнение неразрывности (4), уравнение (3) проинтегрируем по переменной r . Накладывая условие V r = 0 при r = 0 на решение уравнения неразрывности, получим компоненту вектора скорости течения синовиальной жидкости V r . Граничное условие при r = ε , наложенное на компоненту V r , дает модифицированное уравнение Рейнольдса, которое определяет функцию давления p = p ( ф , ^ ).

Уравнение Рейнольдса

Для не осесимметричного течения синовиальной жидкости функция давления зависит от ф и ^ , динамическая вязкость синовиальной жидкости п _Р зависит от ф , r , и ^ . Высота зазора ε может быть функцией переменных ϕ и ξ . Сферические поверхности тазобедренного сустава образуют зазор, где находится синовиальная жидкость. Вращение головки кости с угловой скоростью ω вызывает течение синовиальной

жидкость

е ⁽ фЛ )

R

R

r

O

Головка

d

O 1

_ ф

D

Хрящ еmin

Зазор

Ае3  у x

Ае ₁

Ножка го

R + D + 8 min

Хрящ         z

Синовиальная

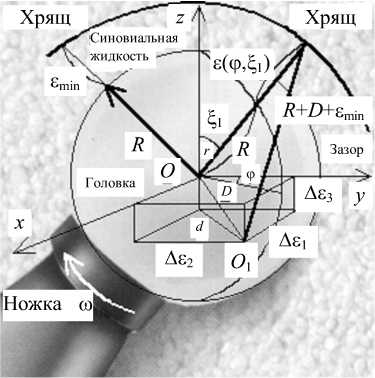
Рис. 5. Сферическая головка эндопротеза и переменная щель

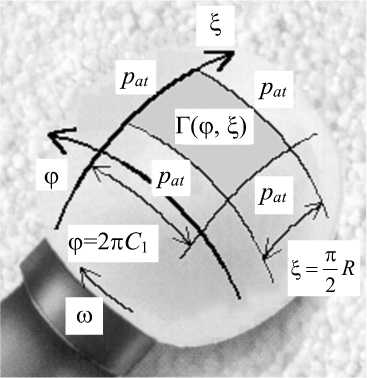
Рис. 6. Область распределения давления на поверхности сферической голвки эндопротеза во время вращения

жидкости в зазоре. Компоненты вектора скорости течения синовиальной жидкости V имеют вид V _ф , V r , V ^ .

Если мы пренебрегаем инерцией и центробежными силами, тогда, после упрощений пограничного слоя, уравнение Рейнольдца для функции давления p ( ф , % ), вызванной вращением, в сферической системе координат принимает вид [27-35]:

Ж Bjpl дфр дф J

+ R ² sin

АР

R Ж

е ³ d p⁽⁰⁾ .П о ^д5

sin

( рх

(э

2 деf £ ]

= 6® R —sin, дф(

Л . Л .

0 <ф< 2 л ^ , 0 <  c <  1, - R <^<- R , ^ = R ^ , 82

где го - угловая скорость вращения головки эндопротеза [1/с], р ₀ - характеристическая вязкость синовиальной жидкости [Па - с], R -радиус головки эндопротеза [м], е - высота зазора [м], p – давление [Па].

Площадь контакта головки эндопротеза

Центр сферической головки эндопротеза расположен в точке O (0,0,0), а центр сферической протезной чаши расположен - в точке O₁(x -Ае ₁, у -Ае ₂, z + Ае ₃). Такое расположение показано на рис. 5-6, где p at означает атмосферное давление [Па], Г ( ф , £ ) - область смазочного слоя [м²], е ( ф , ^) - переменная высота зазора [м].

Контактное давление p ( ф , ^) [Па] головки эндопротеза со сферической поверхностью показано на рис. 7. Окончательно высота зазора имеет следующий вид [27-35]:

е ( ф , ^ 1 ) = f ( ф , ^ 1 ) - R ,                                  (11)

где f ( ф , ^ ₁) = r ₁ положительное решение уравнения:

r ² - 2( Ае ₁ cos ф sin ^ ₁ + Ае ₂ sin ф sin ^ ₁ - Ае ₃ cos ^ ₁) r - ( R + h _min)( R + 2 D + е _min) = 0, (12)

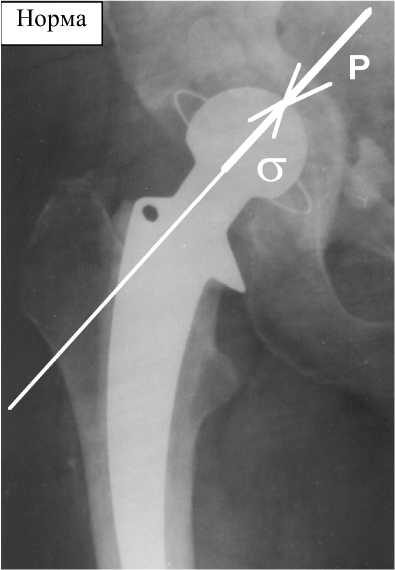
Рис. 7. Тазобедренный эндопротез Веллера после установки. Показаны векторы силы давления и нормальных напряжений

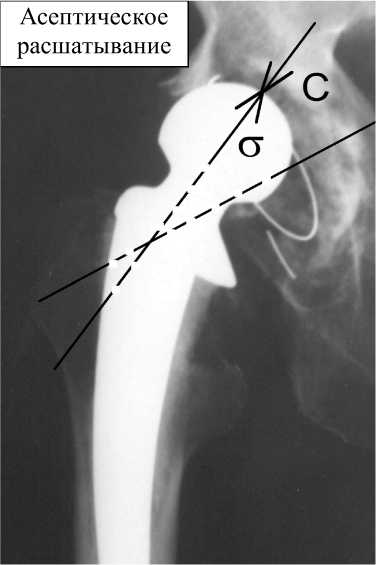
Рис. 8. Асептическое расшатывание протеза Веллера после восьми лет эксплуатации. Показаны векторы силы нагружения и нормальных напряжений

d - 7 Де2+Де 2+Д£2.

где символ D означает эксцентриситет [м] и 5 1 = 5 / R .

Суммарная нагружающая сила и сжимающие напряжения

Суммарная сила нагружения C tot [Н] головки сферического эндопротеза тазобедренного сустава человека получена через поверхностный интеграл следующего вида [27-35]:

с„ -Я Р <». 5) d Г (Ф. 5).(14)

Г ( ф . 5 )

0 <ф<2пс. 0 < c < 1. П R <5<-R. 5-R ^

где JJ(..)dr   - поверхностный интеграл, определенный на поверхности головки эндопротеза, dΓ элемент поверхности.

Суммарные сжимающие напряжения ст [Н/см²] сферической головки эндопротеза тазобедренного сустава человека получены из следующей формулы [2735]:

С

ст--S-.                                   (16)

S ≡ 2 π R ² cos( π /8),

где S – вычисленная область поверхности головки эндопротеза [см²]. Расположения суммарной силы нагружения C tot ≡ C и несущих сжимающих напряжений σ показаны на рис. 8.

Численный анализ рабочих параметров сферического эндопротеза

При численном анализе символ R означает радиус сферической головки протеза [см], e ≡ D – эксцентриситет [ µ м], ω – действительная угловая скорость головки эндопротеза [1/с], η – надлежащее значение вязкости жидкости [Па ⋅ с], p max – вычисленное значение давления [Па], ε min – минимальная высота зазора [ µ м], C tot – вычисленная суммарная сила [Н], описанная формулами (14)-(15), S – вычисленная область поверхности сферической головки [см²], описанная формулой (17) и σ – вычисленные значения сжимающих напряжений [Н/см²], определяемые по формуле (16).

Все параметры: исходные ( R , e = D , ω , η , ε min ) и вычисленные ( C tot , p max , S , σ ) показаны в таблицах 1 и 2. Кроме того, в численном анализе по формулам (1)-(8) считается, что Δε 1 =2 µ м, Δε 2 =2 µ м, Δε 3 =2 µ м.

Численные и графические результаты для функции давления для сферической головки эндопротеза диаметром d = 2,8 [см], полученные путем использования метода конечных элементов и математического пакета Mathcad , показаны на рисунках 9 и 10. Результаты для протеза, где d = 3,2 [см], показаны на рисунках 11 и 12.

Таблица 1

Параметры R , D , ю, n, s_mill, S , использованные при численном анализе напряжений p , силы нагружения C tot и сжимающих напряжений о для сферического эндопротеза при d = 2,8 см

	d =2 R [см]	R [см]	D [ µ м]	ω [1/с]	η [Па ⋅ с]	p max [Па]	ε min [ µ м]	C tot [Н]	S [см2]	σ = C tot / S [Н/см2]
Рис.9	2,8	1,4	0,2	0,25	1,00	3,376·106	1,00	648	5,6889	113,906
Рис.10	2,8	1,4	0,2	0,50	1,00	6,651·106	1,00	1295	5,6889	227,636
—	2,8	1,4	0,2	0,75	1,00	9,927·106	1,00	1943	5,6889	341,542
—	2,8	1,4	0,2	1,00	1,00	13,203·106	1,00	2591	5,6889	455,448

Таблица 2

Параметры R, D, ю, n, E min , S , использованные при численном анализе напряжений p , силы нагружения C tot и сжимающих напряжений о для сферического эндопротеза при d = 3,2 см

	d =2 R [см]	R [см]	D [ µ м]	ω [1/с]	η [Па ⋅ с]	p max [Па]	ε min [ µ м]	C tot [Н]	S [см2]	σ = C tot / S [Н/см2]
Рис.11	3,2	1,6	0,2	0,25	1,00	4,379·106	1,00	1105	7,4303	148,715
Рис.12	3,2	1,6	0,2	0,50	1,00	8,657·106	1,00	2210	7,4303	297,430
—	3,2	1,6	0,2	0,75	1,00	12,936·106	1,00	3315	7,4303	446,146
—	3,2	1,6	0,2	1,00	1,00	17,214·106	1,00	4420	7,4303	594,861

R =0,014 [м]

to =0,25 [1/с]

П =1 [ Па - с] p max =3,376·10⁶ [Па]

£ _min =¹ | ц м|

C tot =648 [Н]

y

6/10

51/10

4п/10

0,027

0,013

31/10

2т/10'

0,013

0,027

p [Па]

15·106

Поверхность слоя смазки =5,6889 [см2]

10·106

p max

5·106

1·105 pat

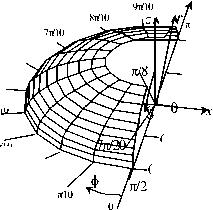
Рис. 9. Распределение давления в сферическом эндопротезе при d = 2,8 см, to = 0,25 1/с

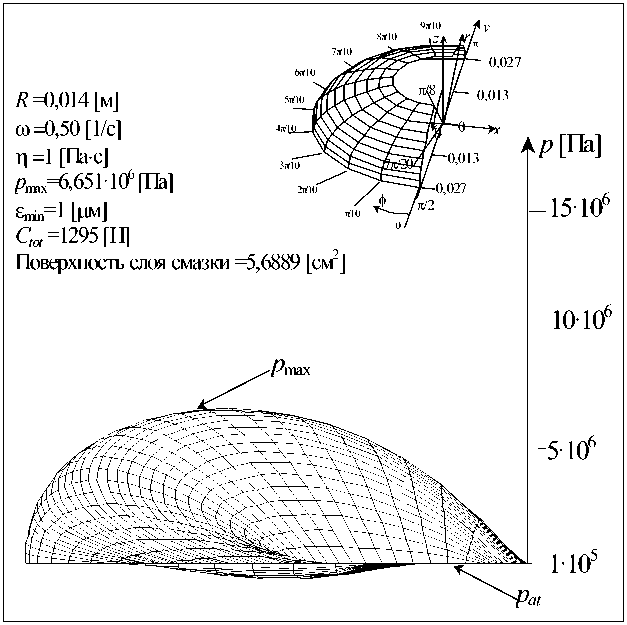
Рис. 10. Распределение давления в сферическом эндопротезе при d = 2,8 см, to = 0,50 1/с

R =0,016 [м] ю=0 , 25 [ 1/с]

П =1 [ Па - с] p max =4,379·10⁶ [Па]

S min =1 [ М м] C tot =1105 [Н]

y

6п/10

5т/10

0,027

0,013

0,013

0.027

p [Па]

15·106

Поверхность слоя смазки =7,4303 [см2]

10·106

p max

5·106

1·105

p at

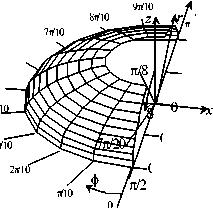
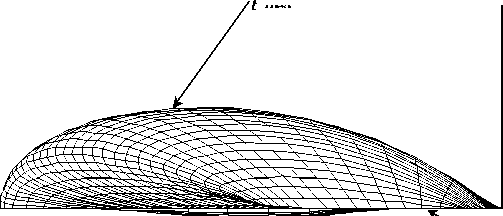
Рис. 11. Распределение давления в сферическом эндопротезе при d = 3,2 см, ю = 0,25 1/с

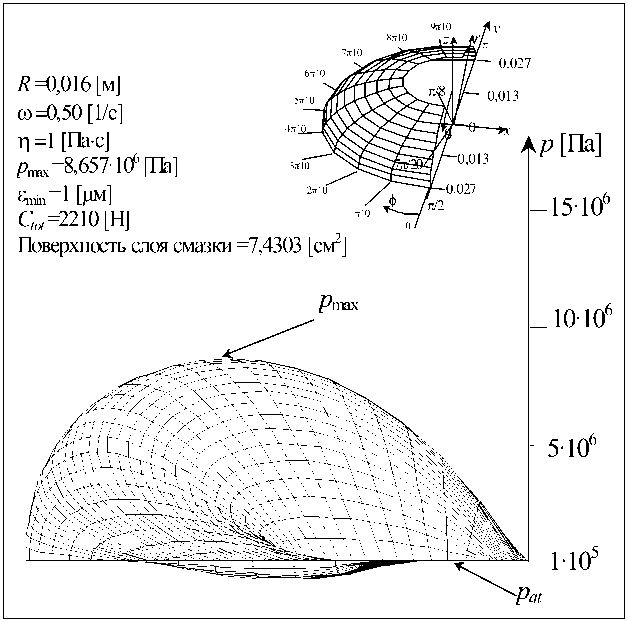
Рис. 12. Распределение давления в сферическом эндопротезе при d = 3,2 см , ю = 0,50 1/с

Графический анализ суммарной силы нагрузки и сжимающих напряжений показан на рисунках 13 и 14.

Выводы

На основе численного анализа можно сделать следующие выводы:

• • Аналитическо-численная    модель гидродинамической смазки

эндопротеза тазобедренного сустава человека со сферическими рабочими поверхностями позволяет анализировать рабочие параметры, такие как давление, нагрузка и сжимающие напряжения.

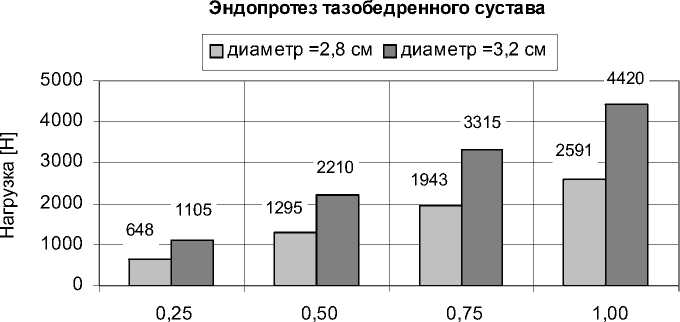
Угловая скорость [1/с]

Рис. 13. Величина нагрузки [Н] в зависимости от угловой скорости [1/с] для сферических эндопротезов ( ∅ 2,8 и ∅ 3,2 см) тазобедренного сустава человека

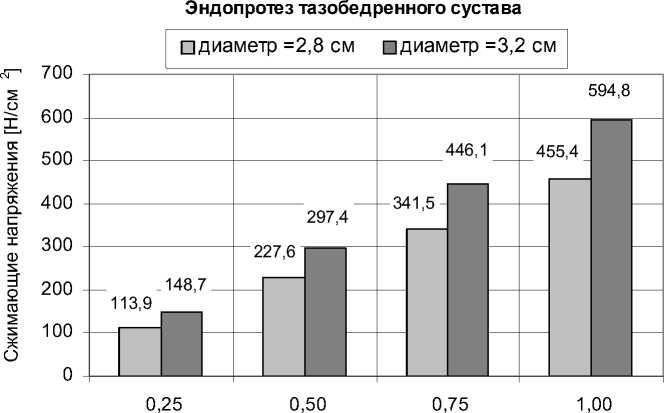
Угловая скорость [1/с]

Рис. 14. Величина сжимающих напряжений [Н/см²] в зависимости от угловой скорости [1/с] для сферических эндопротезов ( ∅ 2,8 и ∅ 3,2 см) тазобедренного сустава человека

• •    Для сферического эндопротеза с исходными параметрами d = 2 R = 2,8 [см], e = 0,2 [ µ м], ω = 0,25; 0,50; 0,75; 1,00 [1/с], η = 1 [Па ⋅ с], ε min = 1 [ µ м] и S = 5,6889 [см²] давление изменяется в пределах от 3,376 ⋅ 10⁶ до 13,203 ⋅ 10⁶ [Па], суммарная нагрузка – от 648 до 2591 [Н] и сжимающие напряжения – от 113,906 до 455,448 [Н/см²].

• •    Для сферического эндопротеза с исходными параметрами d = 2 R = 3,2 [см], e = 0,2 [ µ м],     ω = 0,25; 0,50; 0,75; 1,00 [1/с], η = 1 [Па ⋅ с],     ε min = 1 [ µ м]    и

  S = 7,4303 [см²] давление изменяется в пределах от 4,379 ⋅ 10⁶ to 17,214 ⋅ 10⁶ [Па], суммарная нагрузка – от 1105 до 4420 [Н] и сжимающие напряжения – от 148,715 до 594,861 [Н/см²].

• •    Величины рабочих параметров, полученные для сферического эндопротеза, где d = 2 R = 2,8 [см], меньше, чем у эндопротеза с d = 2 R = 3,2 [см].

Благодарность

Автор благодарит Государственный комитет научных исследований Варшавы (Польша) за поддержку посредством гранта №8-T 11E-021-17. Автор выражает признательность профессору Кжиштофу Вежхольскому из Гдыньского морского университета (Польша) за полезные обсуждения во время написания статьи. Автор также благодарит доктора медицинских наук Яноша Шванека из Жешовского Университета (Польша) за предоставленный протезный материал.