Определение динамических параметров привода экспериментального стенда для исследования карданных передач

Введение. Для прочности и надежности систем приводов, трансмиссионных систем, независимо от области применения (машиностроение, самолетостроение), наибольшую опасность представляют колебательные процессы при приближении к резонансному состоянию [1–4]. Поэтому важной задачей для обеспечения надежности системы приводов является исследование динамической нагруженности элементов привода, которое заключается в определении собственных (свободных) частот колебаний, которые могут возбуждаться в колебательной системе под действием начального толчка, и сравнении их с частотами внешних и внутренних возбуждающих факторов. Для этого необходимо определить основные динамические параметры элементов привода, на основе которых можно будет разработать динамическую и математическую модели привода и исследовать динамическую нагруженность его элементов.

Методы исследования. На кафедре основ конструирования машин был разработан стенд (рис. 1) для исследования карданных передач в режимах, приближенных к условиям эксплуатации, с углом излома карданного шарнира от 0º до 20º [5].

На рис. 2 приведена кинематическая схема испытательного стенда, содержащая следующие блоки: технологическая передача 1 , раздаточная коробка 2 , электродвигатель 3 , испытываемая карданная передача 4 , устройство нагружения 5 .

Для проведения теоретических исследований и анализа внутренней динамики привода стенда необходимо представить его в виде идеализированной многомассовой крутильно-колебательной динамической системы, т. е. системы масс, соединенных между собой упругими и фрикционными связями, с действующими на данную модель возмущающими силовыми факторами.

При построении динамической модели исследуемого привода определялись моменты инерции сосредоточенных масс элементов привода, податливости упругих участков. Моменты инерции вращающихся деталей привода, имеющих простую геометрическую форму, определялись теоретически по общеизвестной методике [1–3] и приводились к валу электродвигателя.

Моменты инерции деталей, имеющих сложную геометрическую форму, определялись экспериментально методом трифилярного подвеса [1; 6; 7], который заключается в следующем: на высоте 2 м на трех тонких нитях (проволоках) подвешивался диск (рис. 3), на диск укладывалась испытуемая деталь с максимально возможным совмещением центров вращения, диск закручивался и отпускался, после чего подсчи-

тывалось количество крутильных колебаний диска за время t .

Момент инерции испытуемой детали может быть определен по формуле

J=

⁽ m дет + m диска

) • g ■ a 2 ■ T ²

16п ■ l

m диска ■ g ■ a 2 ■ T 2

16n ■ l

( кг ■ м 2 ) ,

где T = t / K – период одного колебания, с; t – время эксперимента, с; m дет – масса детали, кг; m диска – масса диска, кг; K – количество колебаний за время t .

Трудоемкость расчетов моментов инерции деталей сложной формы достаточно велика, с увеличением сложности расчетов растет и ошибка, поэтому для таких деталей предпочтительнее экспериментальное определение.

Коэффициенты жесткости (податливости) большинства упругих участков привода также были определены теоретическими [2–4; 8] и экспериментальными методами [9–11], так как теоретические методы не всегда дают удовлетворительный результат.

Имеющие место в приводе стенда изгибные деформации приводились также к крутильным деформациям. Суммарная крутильная жесткость трансмиссионной системы представлялась как сумма крутильных жесткостей валов, контактных жесткостей шлицевых соединений, приведенных к крутильным жесткостям валов, изгибных жесткостей валов совместно с жесткостями опор и зубчатых зацеплений, приведенных к крутильным жесткостям валов [12–15].

Для определения суммарной крутильной податливости коробки перемены передач коробка устанавливалась на специальном стенде [8], первичный вал КПП стопорился (рис. 4). На выходном конце вторичного вала закреплялся рычаг с чашей для грузов на конце.

При помощи рычага и грузов вторичный вал ступенчато нагружался крутящим моментом. На каждой ступени нагружения замерялись углы поворотов конца вторичного вала КПП φ 1 и конца первичного вала КПП φ 2 . Замеры осуществлялись при помощи индикаторных головок. Угол поворота на каждой из ступеней нагружения определялся по формуле

Ф = - (рад),

где φ = φ 1 – φ 2 , рад; Δ – замеренная индикатором длина дуги, мм; R – радиус, на котором производился замер, мм.

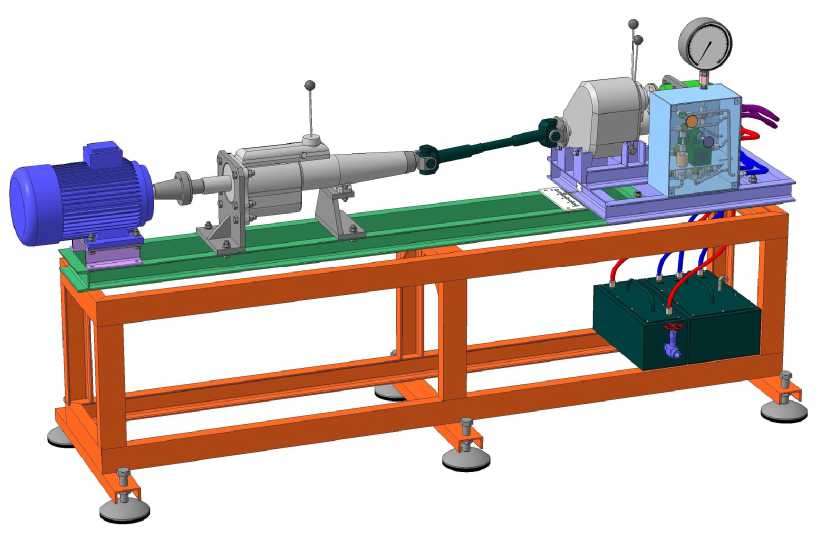
Рис. 1. Модель испытательного стенда

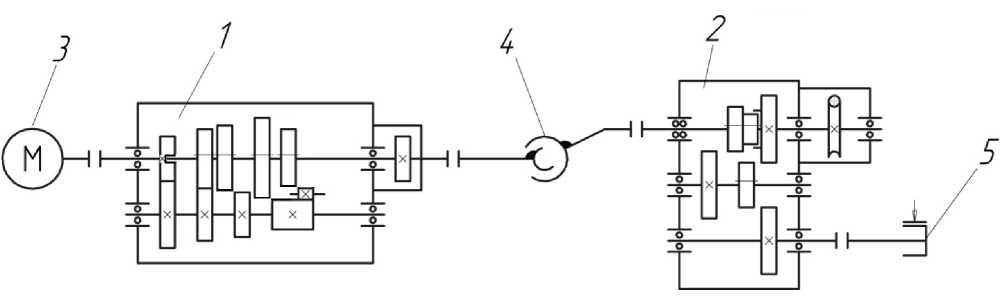
Рис. 2. Кинематическая схема испытательного стенда

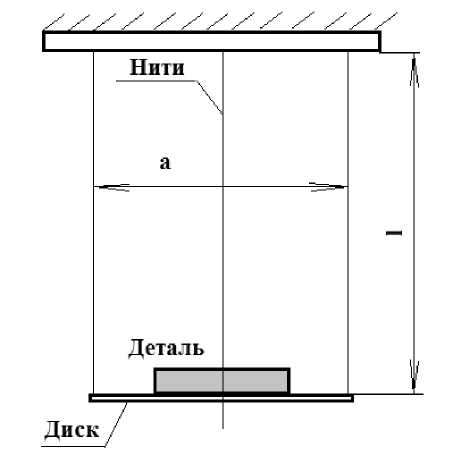
Рис. 3. Определение моментов инерции деталей методом трифилярного подвеса

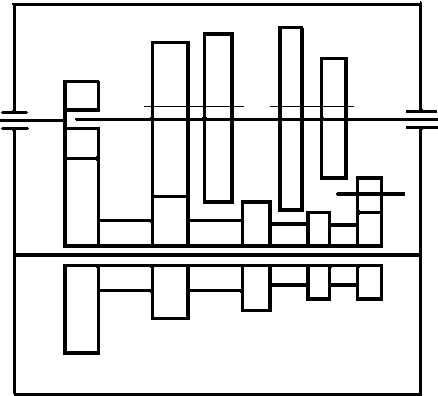
Рис. 4. Схема измерения углов закручивания валов КПП

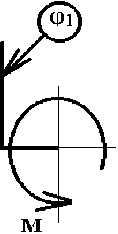
Суммарная крутильная податливость КПП определялась по формуле eсум - -jy- — ^2" ■ i (рад/Н-м),

Мкр Мкр где Мкр - крутящий момент; i - передаточное отношение КПП.

Коробка перемены передач представляет собой сложную изгибно-крутильную систему. Суммарная крутильная податливость ее складывается из податливостей валов на кручение, контактных податливостей шлицевых соединений, податливостей опор и зубчатых зацеплений, изгибных податливостей валов. Для упрощения расчетов изгибные податливости КПП приводятся к крутильным податливостям валов, суммарная крутильная податливость состоит:

– из крутильной податливости валов;

– контактной податливости шлицевых соединений, приведенной к крутильной податливости валов;

- изгибной податливости валов совместно с податливостью опор и зубчатых зацеплений, приведенной к крутильной податливости валов [16; 17].

Аналогично определялись податливости других элементов (участков) привода.

В результате экспериментальных исследований было определено соотношение различных составляющих в балансе крутильной податливости КПП привода стенда на каждой из четырех передач (см. таблицу).

Из таблицы видно, что податливость валов на кручение в среднем составляет 53,75 %, контактная податливость шлицевых соединений – 33 % и изгиб-ная податливость валов совместно с податливостью опор и зубчатых зацеплений – 13,25 % от суммарной крутильной податливости КПП.

Заключение. Сравнение моментов инерции элементов привода, полученных расчетным и экспериментальным методами, показало, что теоретические расчеты выполнены достаточно точно, ошибка не превысила 4 %.

На основе проведенных предварительных расчетов и экспериментальных исследований динамических характеристик элементов привода испытательного стенда была построена расчетная динамическая модель для основных рабочих I–IV передач привода стенда (рис. 5).

На основе уравнения Лагранжа второго рода [18] для полученной динамической модели разработана математическая модель динамики привода испытательного стенда с учетом диссипативных сил и принятых допущений в виде системы дифференциальных уравнений:

J 1 ■Q l ^{+ b} 12 ^(ф 1 ^{— ф} 2 ) ^{+ С}12 ( ф 1 ^{— ф} 2 ) ~ 0,

J 2 ■ ^ф 2 ^{— b} 12 ^(ф 1 ^{— ф} 2 ) ^{— С}12 ^(ф 1 ^{— ф} 2 ) ⁺

^+b 23 ^(ф 2 ^{— ф} 3 ) ⁺ С 23 ^(ф 2 ^{— ф} з ) ^— 0,

J 3 ■ ^ф 3 ^{— b} 23 ^(ф 2 ^{— Ф} 3 ) ^{— С} 23 ^(ф 2 ^{— ф} 3 ) ⁺

^+b34 (< Р 3 ^{— ф} 4 ) + C 34 ( Ф 3 ^— Ф 4 ) ^- 0,

J 4 ■ ^ф 4 ^{— b} 34 ^(ф 3 ^{— ф} 4 ) ^{— С} 34 ^(ф 3 ^{— ф} 4 ) ⁺

^+b 45 (^ф 4 ^—Ф 5 ) + C 45 ( Ф 4 Ф 5 ) ^- 0,

..........................................

J 6 ■ ^ф 6 ^{— b} 56 (^ф 5 ^—Ф 6 ) ^{— С} 56 ( Ф 5 ^— Ф б ) ⁺

^+b 67 ^(ф 6 ^{— Ф} 7 ) ^{+ С} 67 ^(ф 6 ^{— ф} 7 ) ^- 0,

..........................................

J 11 ^11 ^{— b} 1011 (< Р 10 ^—Ф 11 ) ^{— С} 1011 ( Ф 10 ^— Ф 11 ) ^{+ +b} 1112 ^(Ф 11 ^{— Ф} 12 ) ^{+ С} 1112 ^(ф 11 ^{— ф} 12 ) ^- 0,

J 13 ■ ^ф 13 ^b 1213 ^(ф 12 ^Ф 13 ) C 1213 ^(ф 12 ^ф 13 ) ⁺

^+b 1314 ^(ф 13 ^{— Ф} 14 ) ⁺ C 1314 ^(ф 13 ^{— ф} 14 ) ^- 0,

..........................................

J 15 ^ ^ф 15 ^+b 1415 ^(ф 14 ^{— ф} 15 ) ^+С 1415 ^(ф 14 ^{— ф} 15 ) ^{- —} M С ^{( (} ) •

Баланс крутильной податливости КПП для четырех передач

№ передачи	Приведенная крутильная податливость в % от суммарной податливости КПП
	Крутильная валов	Контактная шлицевых соединений	Изгибная валов + опор + зубчатых соединений
I	49	42	9
II	62	27	11
III	50	37	13
IV	54	26	20
Среднее значение	53,75	33	13,25

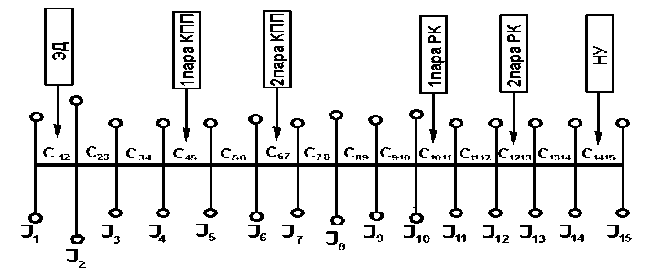
Рис. 5. Расчетная цепная динамическая модель привода испытательного стенда

Рис. 6. Начальное окно APM GYDROTRANS II

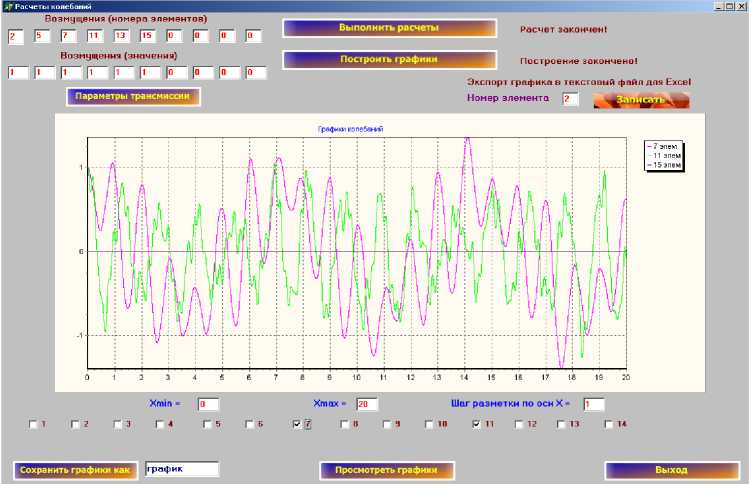
Рис. 7. Рабочее окно APM GYDROTRANS II

Полученная математическая модель позволяет провести теоретические исследования и анализ внутренней динамики привода стенда.

Реализация данной математической модели планируется с помощью АРМ Gydrotrans-II [19; 20], что позволит проверить адекватность модели и точность реализации в программном обеспечении (рис. 6, 7).

Эти исследования в совокупности направлены на получение программно-аппаратного комплекса для совершенствования задач проектирования валопроводов, с учетом их поведения в эксплуатации с использованием как виртуальных инструментов моделирования нагрузочных режимов, так и реальных исследований и доводки с помощью экспериментального стенда и предлагаемой методики научных исследований, что в итоге позволит значительно сократить затраты времени на проектирование с одновременным повышением качества принимаемых проектных решений, а также позволит исследовать уже спроектированные приводы с целью оптимизации их конструктивно-режимных параметров.

Acknowledgments. This work was supported by the Ministry of Education and Science of the Russian Federation in the framework of the implementation of State tasks № 2014/211, № 9.447.2014/к.