Определение дисперсного состава послеспиртовой зерновой барды

Порошкообразные материалы применяются во многих отраслях промышленности. Многие свойства порошков в значительной степени зависят от дисперсности. Анализ дисперсного состава является обязательным методом контроля во всех технологических процессах, связанных с изготовлением и переработкой порошкообразных материалов.

В настоящее время существует несколько методов определения дисперсного состава [1,2]: ситовой анализ, седиментационный анализ, гидродинамические методы, микроскопический анализ. В этом ряду микроскопический метод выгодно отличается тем, что позволяет определить не только геометрические размеры исследуемых объектов, но и увидеть особенности их формы, структуры и строения поверхности.

Микроскопический метод [2] позволяет измерять частицы размером 0,3—100 мкм. Для определения размера частиц меньше 1 мкм применяют электронные микроскопы с более высокой разрешающей способностью, чем оптические.

Исследование дисперсности порошков послеспиртовой зерновой барды путем подбо- ра наиболее оптимального варианта аппроксимирующей функции порошков различной дисперсности.

Важными характеристиками дисперсных материалов являются размеры и форма частиц, распределения которых по гранулометрическому составу определяет такие характеристики, как сыпучесть, транспортабельность, слеживаемость и хранение продукта.

Объекты и методы исследований

Объектом исследования являлась после-спиртовая зерновая барда. В качестве метода исследования применялись методы микроскопического определения размера частиц барды.

Результаты и их обсуждения

Для рационального использования методов транспортировки и хранения после-спиртовой барды было исследовано методом микроскопического определения дисперсного состава продукта.

Исследовано несколько модельных образцов порошков из послеспиртовой зерновой барды (барда отжатая, сухая, восстановленая). Исследуемые порошки различной дисперсности исследовали с помощью USB Digital Microscope. Сняв микроскопическую линейку, получили цену деления микрофотографий.

Для каждого образца снимались не менее 6 полей из разных участков зрения. С помощью программы обработки цифровых фотографий Photo M 1.21 определяли линейные размеры частиц.

Процентное соотношение частиц разного размера определяли по формуле (1):

Qi--=^ • 100,               (1)

где: Ni- число частиц в данной фракции; EN- сумарное число частиц.

Согласно этой формуле, делим количество частиц определенного размера на общее количество частиц и умножаем на 100% [3].

По формуле:

VQ = Qo + Q1+... (2)

По поученным расчетам строим интегральную функцию распределения для отжатой барды (рис. 1), сухой барды (рис. 2), для восстановленной барды (рис. 3)

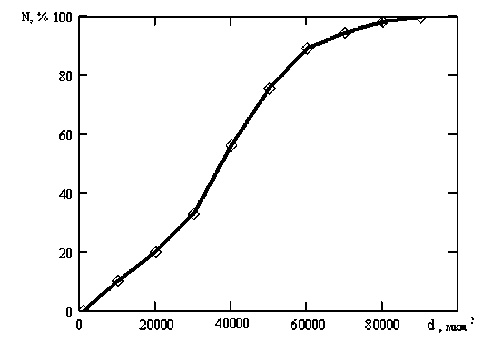
Рис. 1. Интегральная функция распределения для отжатой барды.

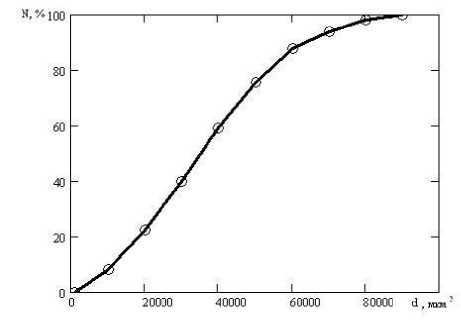
Рис. 2. Интегральная функция распределения для сухой барды.

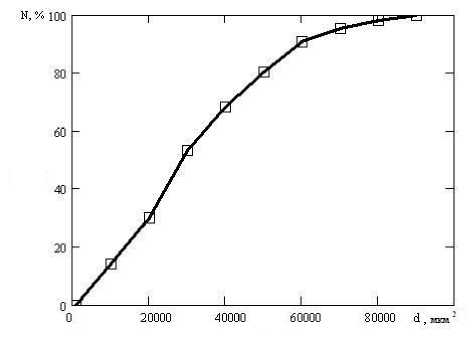
Рис. 3. Интегральная функция распределения для восстановленной барды.

Построение начинали из мельчайших частиц, откладывая их процентное содержание (Qo) на ординате; затем для частиц следующей фракции отложили ординату, равную сумме процентного содержания частиц предыдущей фракции и фракции с большим радиусом, и так далее, работают до тех пор, пока последняя ордината (соответствующая максимальному диаметру) не составит 100%.

Далее с помощью следующих операций, в среде программы Mathcad:

d • = data ^

^{7 1 :} =    l n( z ) *

F ⁽ x , a ) : =

^X 1 ,0 •=¹

X  •=--------- >

¹       ln( d )

X 2 • = d

^a 1

a 1

- x _- e^a o ⁺ a 2 x

• x - e a ^{0 +} a ² x

a + a7x x - e 0   2

a 1 - x ³ - e^a o ^{+ a} 2 x

>

a о • = ( X T - X 1 ) ^{- 1} - X^ a i • = genfit ( d , z , a о , F ) Построим дифференциальную функцию распределения (рис. 4)

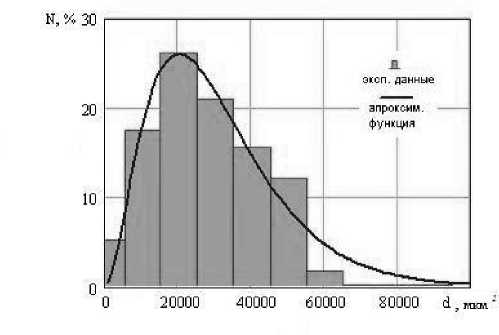
Рис. 4. Дифференциальная функция распределения, на фоне экспериментальной дискретной гистограммы, которая указывает на количество частиц разных размеров (барда отжатая).

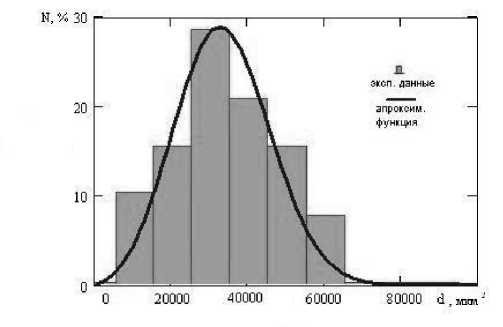
Рис. 5. Дифференциальная функция распределения, на фоне экспериментальной дискретной гистограммы, которая указывает на количество частиц разных размеров (барда сухая)

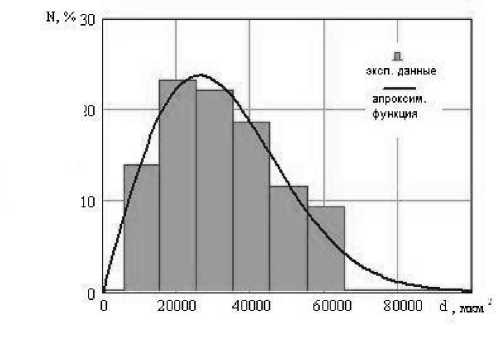
Рис. 6. Дифференциальная функция распределения, на фоне экспериментальной дискретной гистограммы, которая указывает на количество частиц разных размеров (барда восстановленая).

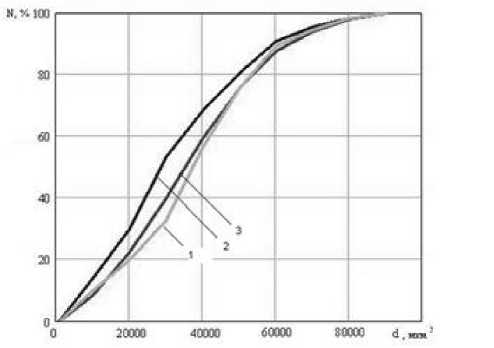
Рис. 7. Интегральные функции распределения для трех модельных продуктов различной дисперсности: 1 - кривая для влажной барды; 2 - кривая для сухой барды; 3 - кривая для восстановленной барды.

Для аппроксимации использовались функции вида: « о • х « ¹ • е « ² "^х для отжатой барды; « 0 • х • е « ¹ '^х+а 2 '^х для сухой барды; « 1 • х • е « ⁰ "« 2 '^х для барды восстановленной. Как видим, они полностью и в точном мере описывают экспериментальные данные и приходятся на экспериментальный максимум, что дает возможность определить наиболее вероятный размер частиц для данного образ-

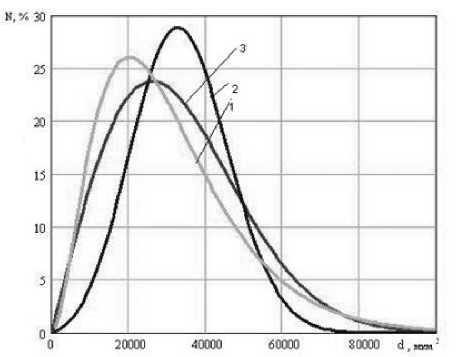
Рис. 8. Дифференциальные функции распределения для трех модельных продуктов различной дисперсности: 1 - кривая для влажной барды; 2 - кривая для сухой барды; 3 - кривая для восстановленной барды.

Заключение

• -    определен размер частиц послеспир-товой зерновой барды методом микроскопирования;

• -    для нахождения оптимальных условий транспортировки и дальнейшего хранения была исследована дисперсность порошков из послеспиртовой зерновой барды путем подбора наиболее оптимального варианта аппроксимирующей функции порошков различной дисперсности;

ца [4]. Интегральные функции распределения для трех модельных продуктов различной дисперсности показаны на рис. 7.

Для определения среднего размера продукта (барда: отжата, сухая, восстановлена) из сырья приводим на одной системе координат все дифференциальные функции распределения (рис. 8).

• -    осуществлена математическая обработка полученных результатов с использованием современных компьютерных программ.