Определение формы образцов для экспериментов на двухосное растяжение

Испытания образцов на одноосное нагружение не позволяют определить механические свойства материалов в полной мере. В дополнение к ним могут проводиться эксперименты при других условиях деформирования — при сдвиге, кручении и иных. Исследователи чаще всего ограничиваются опытами, где под действием одного силового фактора в образце формируется однородное НДС. Распространенность данного рода экспериментов объясняется доступностью и универсальностью испытательного оборудования, наличием разработанных международных стандартов и ГОСТов. Но учитывая данные только лишь стандартных испытаний невозможно спрогнозировать реальное поведение материала со сложным механическим поведением и понять суть процессов, которые в нем происходят.

Эксперименты на двухосное растяжение дают более полную картину поведения материала. В особенности такие исследования необходимо проводить для случаев, когда материал (например резина) существенно меняет свои свойства в процессе нагружения (проявляется эффект размягчения [1, 2], и материал ведет себя вязкоупругим образом [3]).

Одним из способов формирования двухосного НДС экспериментальным путем служит деформирование по двум осям плоских образцов крестообразной формы [4–11] (Рис. 1). При этом возникает ряд трудностей, заключающихся в том, что поле напряжений в центральной области образца не является однородным. Но, в отличие от одноосного нагружения, не существует определенных стандартов на проведение экспериментов, а также на формы и размеры используемых образцов. Помимо образцов крестообразной формы в ряде исследований [6, 9, 10] рассматриваются тонкостенные трубки, нагруженные на концах внутренним давлением, крутящим моментом, растягивающей силой или этими усилиями в различной комбинации. Имеются работы [6, 7, 9, 10, 12], где говорится об опытах на дискообразных образцах, закрепленных по контуру зажимами круглой или эллиптической формы, и нагружаемых внутренним давлением подаваемого газа или жидкости.

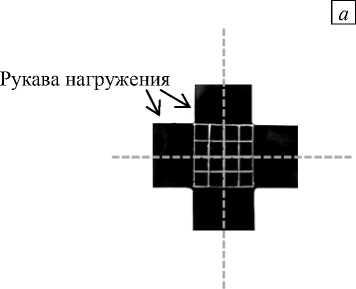
Рис. 1. Вид крестообразного образца с нанесенными на центральную (рабочую) область линиями до ( a ) и после ( б ) растяжения

по обеим осям

Большие возможности для изучения двухосных напряженных состояний со сложной историей деформирования дает двухосная испытательная машина фирмы Zwick. На этом оборудовании можно реализовать различные программы испытаний в зависимости от скорости приложения нагрузки (от 0,001 до 15000 мм/мин) или величины прикладываемых усилий (до 2 кН). Перемещение захватов по каждой оси нагружения является независимым, что позволяет осуществлять различные способы деформирования. Результаты экспериментов считываются с датчиков перемещения и силы, а также с видео экстензометра videoXtens Array, благодаря которому бесконтактным образом измеряются деформации в исследуемой области на основе перемещений меток, нанесенных на образец (Рис. 1).

В обсуждаемой работе анализируются результаты исследования эластомерных материалов, которые практически несжимаемы и работают в условиях очень больших деформаций. В ходе двухосного растяжения у крестообразных образцов из подобных материалов наблюдается формирование неоднородного поля деформаций в центральной области. Для уменьшения неоднородности, то есть создания равномерных полей деформаций и напряжений в рабочей зоне, вносятся различные изменения в геометрию образца, что служит основой для нахождения оптимальной крестообразной формы [4–11]. Для эластомерных материалов первые эксперименты на двухосное растяжение были проведены в 40-х годах на образцах квадратной формы, нагружаемых с помощью многочисленных жестких тяг вдоль каждой из сторон [10, 13]. Сложность эксперимента состояла в обеспечении равномерности закрепления и нагружения образца.

Цель, которая стояла перед авторами данной статьи, заключалась в нахождении оптимальной крестообразной формы на основе количественной оценки однородности полей напряжений и деформаций в центральной части образца. Рассматривались уже известные из литературы модификации такой геометрии, и осуществлялся поиск новых вариантов. Численно найденная оптимальная форма проверялась практически на образцах из наполненной резины при различных программах нагружения на четырехвекторном испытательном стенде Zwick.

2.    Формы крестообразных образцов

При двухосном растяжении в центральной части крестообразного образца (см. область, покрытую линиями, на Рис. 1) в результате неравномерного приложения нагрузки образуется неоднородное поле деформаций. Чтобы это поле было однородным на большей площади, расположенной в центральной области, в литературе предлагаются различные изменения в крестообразной форме образцов. Большинство модификаций формы осуществлялось для образцов из материалов, поведение которых отличается от характерного поведения эластомеров — металлов и композитов [4–7, 9–11]. Однако эти модифицированные формы образцов для двухосного растяжения можно использовать и применительно к эластомерным материалам, как это сделано в статье [8].

В представляемой вниманию работе численно и экспериментально исследовалось влияние на однородность НДС в рабочей зоне образца следующих вносимых изменений:

• –    формы и размера участков С (Рис. 2), находящихся на пересечении рукавов нагружения; в самом простом случае каждый из участков представляет собой прямой угол;

• –    геометрии рукава нагружения, количества и размера тяг — прямоугольных полос материала, на которые нарезаются рукава и которые передают нагрузку к центральной области.

3.    Постановка задачи

Помимо этого, прорубались отверстия малого радиуса в вершинах разрезов, формирующих тяги, чтобы избежать преждевременных разрывов из-за концентрации напряжений и, как следствие, увеличить значение максимальной деформации в центральной части образца.

На основании численного анализа даны оценки различных вариаций формы крестообразного образца из гиперупругого материала. Результаты проверены экспериментально на образцах из вязкоупругих эластомеров.

Все вычисления проводились для крестообразных симметричных образцов одного размера. При построении модели расчетной области задавались постоянная длина зажатого ненагруженного образца

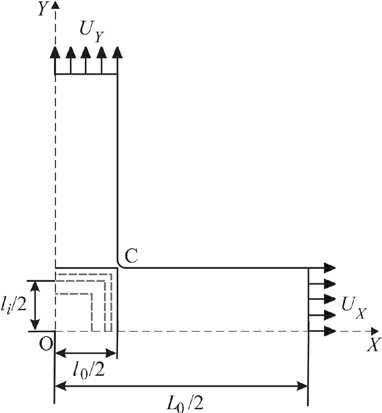
Рис. 2. Схематическое изображение расчетной области образца и граничных условий задачи

Граничные условия были следующими:

- на поверхностях симметрии X       = 0: U X

Y е ^{{ 0;} L о/2 ^}

вне захватов L ₀ = 122 мм для каждого из двух направлений нагружения и размеры сторон центральной области l ₀ = 30 мм (Рис. 2). Отношение длины рукава к длине рабочей зоны составляло 1,5:1. Для всех образцов в рабочей зоне рассматривались произвольные квадратные области разных размеров с целью исследования НДС на предмет однородности и влияния краевых эффектов. Относительная длина сторон любой из этих областей рассчитывалась как кщ = kJl о ( kni <  1 ), где к — длина сторон (в мм) некой i -й области n -го образца.

В рамках поставленной задачи крестообразные образцы равномерно нагружались по двум осям, то есть в четырех направлениях. Граничные условия в местах крепления образца в захватах задавались в виде перемещений. Так как материал образцов (наполненная сажей резина) считается однородным и изотропным, а также в силу симметрии геометрии образца и накладываемых граничных условий, при численной реализации задачи в расчет принималась только четверть образца (Рис. 2).

= ⁰ , ^Т XY = 0 и Y X _б{ о; l 0/2 } = ^{0 :} U y = 0 , ^Т YX = 0 ^;

- на поверхностях нагружения Y X _{б{ 0;}^_{/2 }} = L 0/ 2: U X = 0,    U y = А и = ( X- 1 ) L 0/ 2 и X| Y _{б{ 0;} ^_{/2 }} = L 0/ 2:

U Y = 0, U_X = А и = ( X- 1 ) L ₀/2, где А и — величина перемещения захвата; предполагалось, что кратность удлинения резины в области захватов достигает X = L/L ₀ = 2 вдоль каждой из осей;

• ^{-    на} свободных поверхностях X Y _6{^ _/2; L _{/2 }} = l 0/ 2: О X = ^Т XY = ⁰ и Y X _6{^ _/2; L _{/2 }} = l 0/ 2: СТ у = ^Т XY = 0.

d U ( I 1 , 1 ₂, 1 ₃ )

,

При численном моделировании решалась только нелинейная упругая задача: P, =------------

I       d F

где P _I — тензор Пиола–Кирхгофа I-го рода; F — тензор градиента места; I ₁, I ₂, I ₃ — инварианты правого тензора Коши-Грина; U ( F ) — функция потенциальной энергии деформации. Материал считался несжимаемым 1 ₃ =X 2 X 2 X 2 = det² ( F ) = 1 (где X 1 , X ₂, X ₃ — кратности удлинения) — это стандартное допущение при описании поведения резиноподобных материалов. Функция энергии деформации записывалась для сравнения через три различных упругих потенциала:

• -    неогуковская модель U = С ₁₀ ( 1 1 - 3 ) , где 1 1 =X 2 + X 2 + X 2 , а X i = ( X 1 X ₂ X ₃ ) ¹³ X i , С ₁₀ — материальная константа, подлежащая определению;

• -    модель  Муни-Ривлина   U = С ₁₀ ( 1 1 - 3 ) + С ₀₁ ( 1 ₂ - 3 ) ,  где   1 ₂ = X 2 X 2 + X 2 X 2 + X 2 X 2 ;     С ₁₀ ,   С ₀₁  —

подлежащие экспериментальному определению параметры;

⁵ C _ii

• -    модель Арруда-Бойс U = ц^ —m(Ii - 3 ), где Ц, X_m , Ci — константы, при этом ц и X подлежат =1 х2т-2 m . m

  определению, а C_i находятся из разложения в ряд обратной функции Ланжевена для свободносочлененных цепей модели и составляют С1 = 1/2 , С₂= 120 , С₃= 11/1050 , С4 = 19/7000 , С5 = 519/673750. Значения подлежащих определению параметров каждой из моделей взяты из статьи Арруда и Бойс, где они были подобраны согласно экспериментам на чистый сдвиг, одноосное и двухосное растяжения [7].

4.    Описание результатов расчета

Поставленная задача решалась в условиях плоско-напряженного состояния. Реализация осуществлялась методом конечных элементов с применением метода Ньютона–Рафсона для решения нелинейных уравнений равновесия. Расчетная область разбивалась на треугольные элементы второго порядка интерполяции искомых величин.

Считали, что некая i -я область размером k_ni центральной части каждого n -го образца (Рис. 2) является однородной, если значения главных напряжений о 1 , а ₂ в каждой точке исследуемой площади не превышают среднего значения главных напряжений c O ₂ в центральной точке О на величину большую, чем 5 = 5 %. Разброс значений перемещений точек вдоль границ этой области также не должен был превосходить 5 . Очевидно, что для областей малых размеров, находящихся вблизи центра, напряженно-деформированное состояние однородно в пределах указанной точности. Следовательно, необходимо было установить максимальные размеры квадратной области, где разброс значений напряжений и деформаций не превышает 5%. Такую однородную область называли предельной.

Согласно введенным обозначениям оптимальная форма определялась относительно размеров максимальной площади однородных областей у образцов различной геометрии, а также с учетом разброса напряжений во всей центральной части образца, чтобы исключить сильное влияние краевых эффектов. Понятно, что у образца оптимальной формы участок, который находится в условиях равномерного двухосного растяжения, должен быть наибольшим. Помимо этого во всех образцах рассматривались области с размерами сторон к _все1 = 0,8 и к _все2 = 0,93 , чтобы отследить тенденцию изменения НДС для различных форм и влияние краевых эффектов. Эти области были выбраны произвольно, с учетом удобства обработки численных данных.

При построении крестообразного образца первое, что необходимо было определить, — это форму и размер участка С на рисунке 2, чтобы избежать возможных разрывов здесь из-за высокой концентрации напряжений при двухосном нагружении. Форму участка С можно задать, к примеру, с помощью внешнего (вариант 1 ) или внутреннего (вариант 2 ) сопряжений сторон рукавов, спрямляющих линий (вариант 3 ), вырезов различного радиуса (вариант 4 ) (Рис. 3). В статье Абделхая и других [4] представлены расчеты для металлических образцов с учетом форм 1 – 3 , форма скругления 4 использована в [14]. Как и в работе [4], на основе статистических оценок разброса напряжений в областях с к _все1 = 0,8 и к _все2 = 0,93 при задании форм участка С одинаковых размеров ( r = R - 1 ₀ /2 = a = г _выр ) было получено, что формы концентратора вида 1 и 3 наименьшим образом повлияли на неоднородность разброса напряжений в исследуемой области. Однако в случае 3 из-за двух образовавшихся концентраторов при больших деформациях могут произойти разрывы. Поэтому все последующие расчеты проводились на образцах со скруглениями малого внешнего радиуса r (см. вариант 1 ). Другими параметрами варьирования формы образца были число разрезов на рукавах образца и их расположение. Наличие разрезов на рукавах существенно влияет на изменение НДС, что подтверждает результаты, описанные в статье [8].

Поскольку компьютерное моделирование проводилось с целью создания максимально равномерных полей напряжений и деформаций при экспериментальном растяжении образцов, то количество наносимых

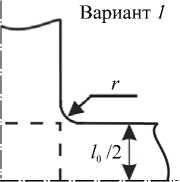
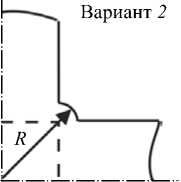
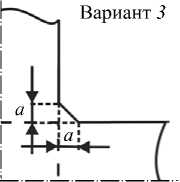
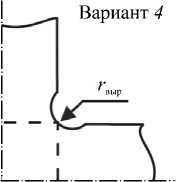
Рис. 3. Схема возможных вариантов формы участков С – зон сопряжения рукавов и центральной области образца разрезов определялось исходя из технологической целесообразности, а именно, 1) заданных геометрических размеров рукавов образца, 2) варьируемых значений радиусов отверстий в устьях разрезов и 3) расстояний между центрами контуров отверстий.

Независимо от размеров радиусов отверстий в вершинах разрезов было подтверждено, что с увеличением количества разрезов в рукавах однородные поля напряжений и деформаций занимают большую площадь рабочей зоны [8, 11]. Все представленные ниже результаты были получены при описании функции энергии деформации в постановке задачи с помощью гиперупругой модели Арруда-Бойс. При использовании других потенциалов — неогуковской модели или модели Муни-Ривлина, сохраняется только качественная картина напряженно-деформированного состояния.

а

б

в

г

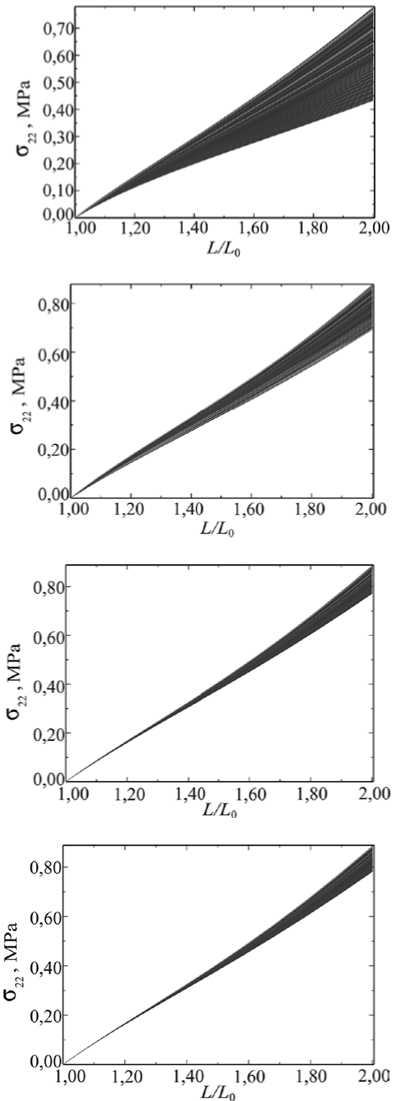
Рис. 4. Вид четырех крестообразных образцов, нагруженных по двум осям ( Х = L[L ₀ = 2 в области захватов), семейство деформационных кривых в каждом узле области со стороной к _все1 = 0,8 (покрыта серой сеткой), а также площадь максимальной области, в которой создается однородное НДС (выделенный квадрат со стороной к ): рукав сплошной без разрезов, к 11 » 0,24 ( а ); рукав с 4-мя тягами, к ₂₁ ~ 0,43 ( б ); с 10-ю тягами, к ₃₁ ~ 0,5 ( в ); с 30-ю тягами, к ₄₁ « 0,52 ( г )

На рисунке 4 показаны результаты численного эксперимента для четырех образцов, демонстрирующие влияние количества тяг на равномерность НДС в рабочей зоне образца. Наглядно видно, что при наличии разрезов границы областей со стороной к _все1 = 0,8 (области обозначены серой сеткой) в меньшей степени изменили свою форму. В ходе же нагружения образца без разрезов (Рис. 4 а ), максимальное значение, на которое деформировалась граница этой области, достигает 61,8% и варьируется в диапазоне до 42,2%. Для образца с 3-мя разрезами (4-мя тягами) (Рис. 4 б ) минимальное значение составляет 69,1% с разницей в 8,1% по сравнению с максимальным значением, с 9-ю разрезами — 73,7–79,7% (Рис. 4 в ). Таким образом, с нанесением большего числа разрезов, во-первых, достигается однородность поля перемещений на большей площади, во-вторых, растет уровень деформаций в центральной части, то есть прикладываемая к образцу нагрузка в большей степени передается на рабочую зону образца.

Для анализа поля напряжений в каждом из образцов на рисунке 4, помимо их деформированной геометрии, представлены также совокупности кривых нагружения, полученные в узлах одинаковой для всех образцов области с квсе1 = 0,8 . Случай (Рис. 4г) является экспериментально непригодным, так как ширина тяг, передающих нагрузку рабочей зоне, мала, и изготовление образцов с таким количеством разрезов практически неосуществимо. Образец представлен только для сравнения. Видно, что увеличение количества тяг способствует формированию однородного поля напряжений на большей площади. Например, при деформировании рабочей зоны на 75% для всех форм образцов происходят незначительные изменения в размерах области однородности, поэтому можно считать, что в образце со сплошными рукавами (одна тяга) область однородности остается квадратом со стороной к11 ® 0,24 , для образца с 4-мя нарезанными тягами — к21 ® 0,43 , для образца с 10-ю нарезанными тягами — к31 ~ 0,5 .

Однородное поле напряжений занимает большую площадь центральной области, поскольку тяги, а не сплошной рукав, делают податливее ее края и позволяют свободнее деформироваться в направлении нагружения. Очевидно, что если уровень деформаций в центральной области образца будет меньше, то область однородности увеличится. Так, при деформации рабочей зоны на 33% размер стороны однородной области образца с 10-ю тягами увеличивается до к 32 ® 0,68 .

Множественные тяги, образующие рукав нагружения, при двухосном растяжении удаляются друг от друга по мере деформирования рабочей зоны, что способствует более равномерному приложению к ней нагрузки. Однако ширина рукава в месте захвата не изменяется, поэтому ближние к осям симметрии тяги передают большую нагрузку, чем удаленные к краям.

Было рассмотрено предположение о неравномерном нанесении разрезов как способе перераспределения прикладываемой нагрузки. Оказалось, что формирование в рукавах образца областей сгущения разрезов, как по направлению к осям симметрии, так и к краям рукавов, не приводит к выравниванию НДС. Наоборот, лучший результат получается при равномерном расположении разрезов.

Еще одним возможным параметром варьирования в образце с разрезами является значение радиуса пробиваемых в устье разрезов отверстий. Эти отверстия служат единственной цели — уменьшению концентрации напряжений. Использование одинакового количества разрезов в рукавах образцов, но с отверстиями, радиусы которых отличаются в 2,5 раза, позволило установить, что при одинаковой степени деформирования рабочей части площадь области однородности НДС увеличивается несущественно. Но при движении к краям рабочей зоны неоднородность нормальных напряжений в ней возрастает в процентном отношении при отверстиях большего радиуса. Последующие исследования показали, что эффективнее делать больше разрезов с малым радиусом отверстий: нагрузка равномернее передается к центральной области и уменьшается влияние краевых эффектов.

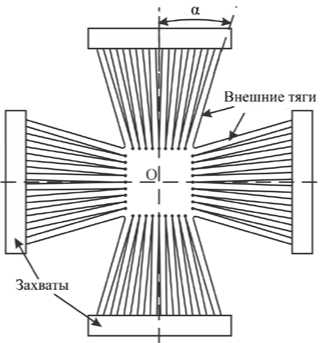
Рис. 5. Вид веерообразного образца

Результаты анализа полученных распределений полей напряжений и перемещений, а также зрительное наблюдение за формой деформированного образца побудили изменить форму рукавов нагружения для улучшения НДС в рабочей зоне образца.

Итак, при двухосном растяжении размеры рабочей зоны увеличиваются, и ширина рукавов в местах перехода в рабочую зону растет, в то время как в области захвата ширина рукавов остается постоянной. Вследствие этого по краям образца — по внешним тягам рукава, в отличие от тяг, расположенных вблизи оси симметрии, нагрузка передается под некоторым углом, и рабочая зона деформируется в центре в большей степени, чем по краям. Для того чтобы при растяжении каждая из тяг оставалась перпендикулярной граням деформированной центральной области, предложено концы тяг в области захватов раздвинуть друг от друга на некоторые равные расстояния (Рис. 5). Для исключения крутящих моментов в тягах

(в местах их перехода в рабочую зону) разрезы на рукавах изначально делались под некими углами по отношению к оси симметрии. При таком веерном расположении тяг в образце потребовалось введение понятия угла раскроя а — угла, под которым располагается внешняя тяга рукава относительно оси растяжения.

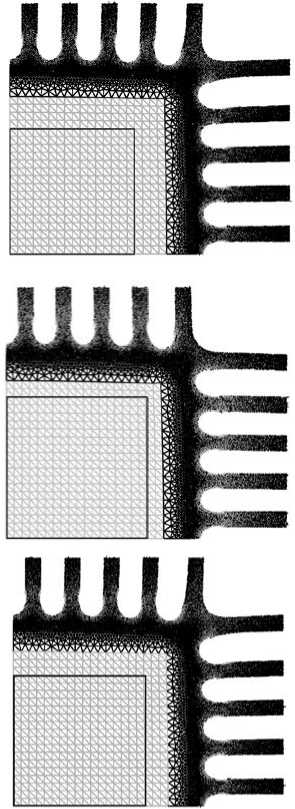
На рисунке 6 представлены поля напряжений для веерообразных образцов с 10-ю тягами и различными углами раскроя а : 10°, 13°, 18 ° . От значения угла раскроя зависит длина внешних тяг, а следовательно, однородность НДС. Для образцов с разными а при одинаковой заданной величине деформации рабочей зоны получилось различное расположение тяг относительно ее деформированного вида. Так, при а = 10 ° размеры стороны рабочей зоны стали больше заданного размера ширины рукава в захвате; в случае а = 13 ° тяги располагаются практически перпендикулярно деформированной рабочей зоне; при а = 18 ° ширина рукава в захвате превышает размеры деформированной стороны рабочей зоны.

Расчеты показали, что при одинаковом уровне деформаций областей с однородным НДС в рабочей зоне ( ® 80,7 %) размеры рабочих зон являются следующими: к ₅₁ ® 0,63 (для а = 10 ° ), к ₆₁ ® 0,73 (для а = 13 ° ) и к ₇₁ ® 0,68 (для а = 18 ° ). На основе полученных данных можно предположить, что расположение тяг влияет на область однородности. Но здесь необходимо учитывать, что у образцов с веерообразной нарезкой тяг изменение однородной области будет отличным от случая, когда разрезы параллельные. А именно, по мере нагружения веерообразного образца до состояния, когда тяги становятся параллельными друг другу, однородная область будет расти; после нарушения параллельности она будет уменьшаться. Кроме того, при задании большого угла раскроя разница в длине тяг существенно повлияет

а

б

в

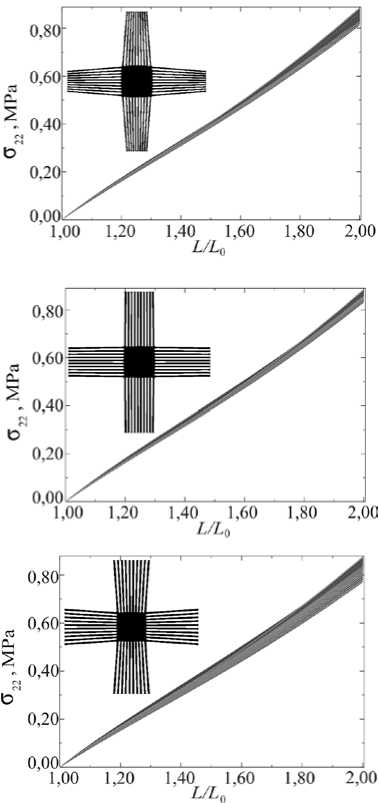
Рис. 6. Влияние угла раскроя а на НДС рабочей зоны при деформации центральной части образца, равной 80,7%: семейство деформационных кривых в каждом узле выделенной серой сеткой области со стороной к все 1 = 0,8 и площадь области, в которой создается однородное НДС (выделенный квадрат со стороной к ^. ): к 51 « 0,63 для а = 10 ° ( а ); к 61 « 0,73 для а = 13 ° ( б ); к 71 « 0,68 для а = 18 ° ( в )

на начальное однородное состояние. К примеру, при а = 18 ° на начальных этапах нагружения однородная область имеет размеры к 72 « 0,59 . При достижении тягами состояния параллельности площадь области с однородным НДС также не будет максимальной, так как внешние тяги деформируются в меньшей степени, следовательно, область, расположенная ближе к оси симметрии, будет нагружаться в большей степени. Таким образом, угол раскроя играет важную роль, и при его определении следует исходить из конкретных размеров образца и параметров удлинения.

5.    Эксперименты

На практике деформирование образцов из вязкоупругого материала (резины) осуществлялось с помощью двухосной испытательной машины фирмы Zwick. Проводимые эксперименты представляли собой циклическое и в одном направлении равномерное двухосное растяжение крестообразного образца (Рис. 7) при малых и высоких скоростях нагружения.

Рассмотренные при численных расчетах для случая гиперупругого материала формы крестообразных образцов были теми же, что и в экспериментах над эластомерным материалом со сложным поведением. В основу вычислений положены простые модели, которые характеризуют резину как высокоэластичный материал, способный испытывать большие деформации и упруго восстанавливаться после снятия нагрузки. При задании определяющих соотношений учтены как нелинейное поведение материала, так и значительное изменение формы тела, достигающее сотен процентов. Гиперупругие модели адекватно описывают реальное поведение резин при очень малых скоростях нагружения, либо, наоборот, при столь больших скоростях, что в материале не успевают проявиться релаксационные процессы. Более того, на практике было интересно соблюсти условие, согласно которому вне зависимости от выбора модели, которая участвует в расчетах, или свойств исследуемого материала (то есть для любых высокоэластичных полимерных материалов) вносимые в геометрию образца изменения приводили к однородности напряженно-деформированного состояния на большей площади исследуемой рабочей зоны образца.

При равномерном двухосном растяжении и любых скоростях приложения нагрузки наглядно прослеживались зависимости, характерные для численного расчета в случае гиперупругого материала, а именно: влияние на однородность поля деформаций количества разрезов в рукавах образца, размеров отверстий в устьях разрезов, формы рукава нагружения. В ходе испытаний, проводимых с помощью видеоэкстензометра videoXtens Array, бесконтактным образом определялось поле перемещений в рабочей зоне образца путем отслеживания изменения формы прямых линий, заранее нанесенных на образец. При одинаковом уровне нагрузок в образце с веерным расположением тяг достигается однородное напряженно-деформированное состояние на площади рабочей зоны большей, чем у образца, на рукавах которого сделаны параллельные разрезы (Рис. 7).

Рис. 7. Вид растянутых крестообразных образцов с различным разрезанием рукавов нагружения: параллельное ( а ), веерное ( б )

6.    Выводы

В данной работе численно, с помощью метода конечных элементов, проведена оптимизация формы крестообразного образца для экспериментов на двухосное растяжение. Критерием оптимизации служила однородность напряженно-деформированного состояния на максимальной площади в центральной части образца с учетом разброса напряжений во всей рабочей зоне (чтобы исключить сильное влияние краевых эффектов). При нахождении оптимальной формы рассматривалось влияние следующих параметров:

• –    углов в месте сопряжения двух рукавов нагружения крестообразных образцов;

• –    количества разрезов в рукавах нагружения;

• –    формы рукавов нагружения.

В результате численных расчётов в среде ABAQUS и экспериментов показано, что при высокой кратности удлинения образца в области захватов (до X = 2 ) и веерообразном закреплении тяг достигается равномерность поля деформаций в рабочей зоне на максимально большой площади. При выбранных размерах образца ( L 0 = 122 мм, l ₀ = 30 мм) область однородного распределения НДС покрывает 73% центральной области образца.

Веерный способ закрепления тяг при нагружении крестообразного образца по двум осям позволяет равномерно передавать нагрузку к рабочей зоне и создает условия для ее более свободного деформирования. Однако особое внимание следует уделять заданию угла раскроя и придерживаться того, чтобы при изготовлении образца угол раскроя не превышал значения, подобранного для конкретных размеров образца и параметров задаваемого удлинения.

Работа выполнена при финансовой поддержке РФФИ (проект № 12-08-00740-а, № 13-01-96016-р_урал_а), программы МИГ (соглашение № С26/627) и Программы РАН 12-С-1-1015.