Определение и оценка прогнозных моделей качества для интегральных микросхем с использованием теории распознавания образов

Поиск математических прогнозных моделей для определения состояния изделий через определенное время – один из эффективных способов влияния на бесперебойную работу аппаратуры, особенно устанавливаемую на борт космических аппаратов. Результаты такого подхода к прогнозированию состояния изделий можно использовать на этапе изготовления аппаратуры. Кроме того, около 30 % отказов и дефектов электрорадиоизделий (ЭРИ) не могут быть определены и выявлены с помощью существующей системы технологического контроля и приемочных испытаний [1]. Таким образом, развитие методов индивидуального прогнозирования (ИП), при которых выдвигается предположение о существовании стохастической связи между начальными значениями информативных параметров и уровнем надежности [2–5], выглядит весьма перспективно в сложившейся ситуации.

В связи с большой номенклатурой ЭРИ особое внимание необходимо уделять физико-химическому анализу отказов, механизмам их возникновения, закономерностям, приводящим к отказам изделий. Таким образом, ставится задача поиска информативных параметров, начальные значения которых можно определить при изготовлении аппаратуры с существующим метрологическим обеспечением на производстве, с необходимой точностью и достоверностью. Кроме того, для исключения разрушающего воздействия на элементы необходимо рассматривать возможности применения методов и средств диагностического неразрушающего контроля [6; 7].

В работе приводятся результаты поиска прогнозных моделей для партии интегральных микросхем. В качестве рассмотренных методов были выбраны метод регрессионных моделей и метод дискриминантных функций с использованием теории распознавания образов. Оценку партии микросхем, представляющей собой генеральную совокупность, целесообразно произвести на выборке, состоящей из 50 экземпляров. Было установлено, что в качестве информативных параметров необходимо рассмотреть время задержки по переднему фронту сигнала t +р ( x 1 ) и критическое питающее напряжение Е кр п ( x 2 ). В качестве прогнозируемого параметра, по которому проводится оценка состояния изделия, выбран дрейф тока утечки ( y ) по прошествии 1000 часов испытаний. Значения параметров экземпляров выборки представлены в таблице.

В некоторых случаях вместо прогнозной модели достаточно знать класс, к которому относится экземпляр из выборки. В большинстве случаев рассматривают два класса: класс годных изделий и класс потенциально дефектных изделий. Для этого вводится граничное значение прогнозируемого параметра, для рассматриваемой выборки равное 60. Таким образом, можно для каждого экземпляра определить фактический класс принадлежности. Экземпляр принадлежит к классу годных изделий, если значение прогнозируемого

Таблица. Значения информативных x ₁, x ₂ и прогнозируемого y параметров экземпляров выборки Table. Values of informative x ₁, x ₂ and predicted y parameters of sample instances

№ экз. x1 x2 y(1000) К, факт № экз. x1 x2 y(1000) факт 1 5,2 1,7 54 1 26 5,4 2,7 92 2 2 4,9 1,5 28 1 27 7,5 2,7 114 2 3 4,1 1,45 39 1 28 6,2 2,8 71 2 4 4,7 1,35 32 1 29 4,4 1,7 39 1 5 4,2 1,3 29 1 30 7,2 1,8 56 1 6 5,6 2,2 51 1 31 6,4 2,1 68 2 7 6,5 1,8 46 1 32 3,8 1,1 32 1 8 6,3 1,9 132 2 33 6,9 2,9 69 2 9 4,4 1,5 53 1 34 4,3 1,2 33 1 10 5,1 1,7 55 1 35 5,6 1,6 37 1 11 12,4 3,1 174 2 36 6,9 2,8 82 2 12 3,9 1,7 50 1 37 5,7 2,5 43 1 13 7,5 2,2 76 2 38 6,4 2,5 48 1 14 4,9 1,3 38 1 39 3,8 1,25 23 1 15 3,8 1,2 33 1 40 4,9 1,5 45 1 16 3,5 1,1 28 1 41 9,2 2,8 147 2 17 5,7 1,6 64 2 42 7,4 2,7 135 2 18 6,9 2,9 47 1 43 4,2 1,5 34 1 19 7,1 2,3 82 2 44 7,1 2,8 88 2 20 10,3 2,5 106 2 45 4,9 1,6 77 2 21 4,4 1,9 68 2 46 4,1 1,5 41 1 22 3,8 1,6 44 1 47 3,5 1,1 19 1 23 3,7 1,5 31 1 48 4,7 1,8 44 1 24 11,5 3,2 133 2 49 4,3 1,6 56 1 25 6,5 2,8 85 2 50 5,4 2,6 53 1 параметра является величиной, меньшей граничного значения. В ином случае - экземпляр принадлежит к классу потенциально дефектных изделий.

Линейный регрессионный анализ - один из самых распространенных способов описания связи между параметрами и зависимой величиной. Модель линейной регрессии имеет вид y (x, b) = b0 + bi xi + b2 x 2 + ...+ bkxk, (1) где bi - коэффициенты регрессии; xj - регрессоры (параметры); k - количество регрессоров (параметров). Коэффициенты линейной регрессии bi показывают скорость изменения переменной y по данному параметру при фиксированных остальных параметрах. Таким образом, определение регрессионной модели сводится к поиску коэффициентов bi.

Для рассматриваемого случая прогнозная модель для каждого j -го экземпляра будет иметь вид y *( j ) ( t np ) = B 0 + B 1 X 1⁽ j ) + B 2 X 2⁽ j ) , (2) где y ⁽ j ) ( t_n p ) - оценочное значение y для j -го экземпляра к моменту времени t ; x i j ) , x 2 j ) - значение х i и х 2 признака j -го экземпляра; B о , B i ,

B ₂ – постоянные коэффициенты регрессионной модели [8].

Метод дискриминантных функций заключается в определении функции, разделяющей пространство признаков на две области, соответствующие двум классам K i и K 2 . В рассматриваемом случае два класса соответствуют классу годных ( K ₁ ) и классу потенциально дефектных изделий ( K ₂ ). Дискриминантная функция имеет вид [9]:

g ( x _i , x 2,..., x k ) = B 1 x 1 + B 2 x 2 + ...+ B k x k , (3) где g ( x i , x 2,..., x k ) - функция гиперплоскости в гиперпространстве признаков; B_k – коэффициенты дискриминантной функции; x_k - признаки (параметры); k – количество признаков (параметров). Для рассматриваемого случая прогнозная модель имеет вид

^П g = y * j ) ( t np ) + B i x i j ) + ^B 2 x 2⁽ j ’ , (4) где П g - порог дискриминантной функции; у ⁽ j ) ( t np ) - оценочное значение y для j -го экземпляра к моменту времени t_n p ; x i j ) , x 2 j ) - значение х i и х 2 признака j -го экземпляра; B i , B ₂ - коэффициенты дискриминантной функции.

20       40       60       80      100     120      140      160      180

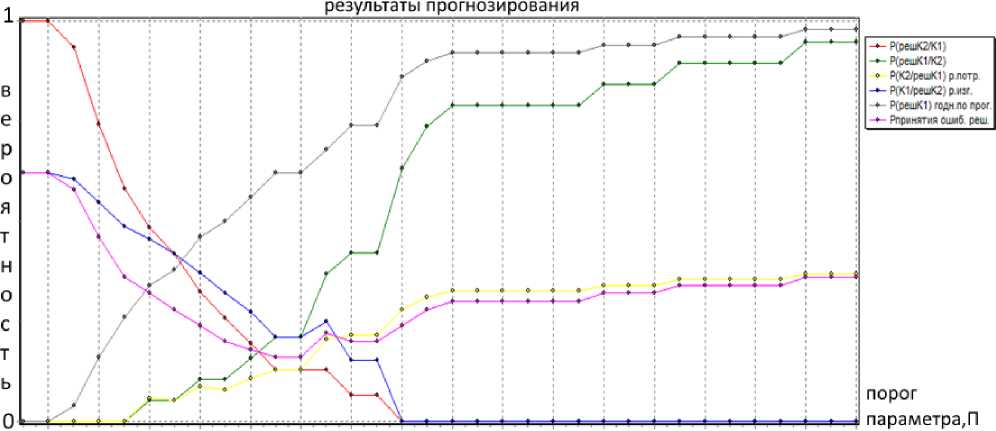
Рис. 1. График зависимости основных вероятностных характеристик от значения порога параметра

Fig. 1. Graph of dependence of the main probabilistic characteristics on the value of the parameter threshold

результаты прогнозирования

: порог дискр.

♦ t • • ♦ t • t • t ♦ ♦ t.t t J ф-ции, rig

16    18    20    22

-*- Р(решК2/К1)

-^ Pl решК1/К2)

• P(K2/petuK1) p norp.

-*- Р(К1/решК2) p изг

-♦ PtpewKl) годи no npor.

-^ Рпрмнятмя ошиб реш

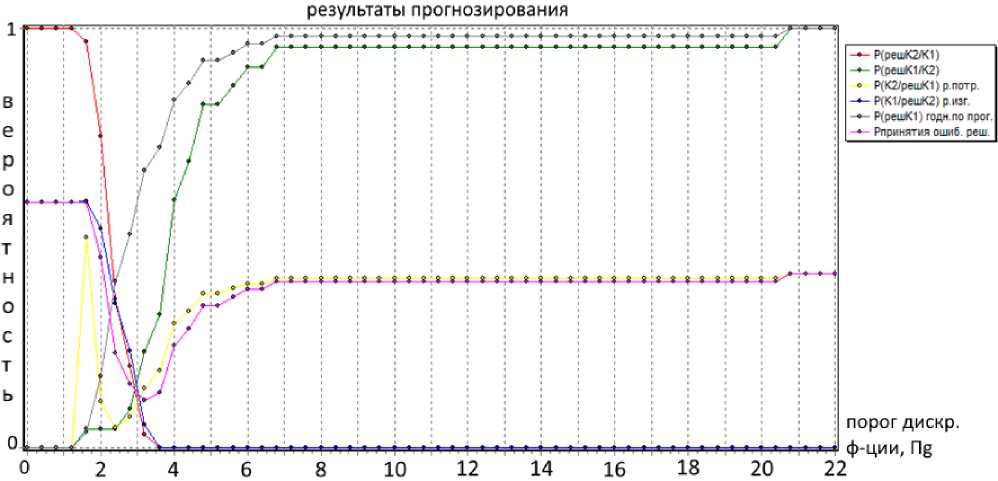
Рис. 2. График зависимости основных вероятностных характеристик от значения порога дискриминантной функции

Fig. 2. Graph of the dependence of the main probabilistic characteristics on the threshold value of the discriminant function

Для рассматриваемой выборки интегральных микросхем индивидуальное прогнозирование с помощью метода регрессионных моделей позволило получить прогнозную модель вида y = -44,56 +17,62x1 + 2,98x2. (5)

Изменение основных вероятностных характеристик с изменением порога параметра показано на рис. 1.

Индивидуальное прогнозирование с помощью метода дискриминантных функций позволило получить прогнозную модель вида

П g = У ( t np ) + 1,08 x i + 0,91 x 2 .

Изменение основных вероятностных характеристик с изменением порога дискриминантной функции отражено на рис. 2.

Исследование моделей показало, что для оператора индивидуального прогнозирования интегральных микросхем, найденного с помощью метода регрессионных моделей, оптимальное значение порога будет равно П = 65 при значении вероятности принятия ошибочных решений Pош = = 0,16. При этом риск потребителя Pпт. = 0,129, риск изготовителя Pизг = 0,211. Минимальное значение Pпт. min = 0 наблюдается при П = 0…35. При этом Pош = 0,36…0,62; Pизг. = 0,487…0,62.

Для оператора индивидуального прогнозирования интегральных микросхем, найденного с помощью метода дискриминантных функций, оптимальное значение порога будет равно П _g = 3,2 при значении вероятности принятия ошибочных решений P _ош = 0,113. При этом риск потребителя P пт = 0,143, риск изготовителя P _изг = 0,056. Минимальное значение P _{пт. min} = 0 наблюдается при П = = 0…1,2. При этом P _ош = 0,585; P _изг. = 0,585.

Заключение

На основе методов дискриминантных функций и регрессионных моделей с использованием теории распознавания образов построены математические модели для прогнозирования показателей качества и надежности интегральных микросхем серии 564. Проведено исследование данных моделей. Установлено, что оптимальное значение порога дискриминантных функций составляет П _g = 3,2. При этом обеспечивается вероятность принятия ошибочных решений Р _ош = 0,113. Оптимальное значение порога регрессионной функции составляет П = 65 при вероятности принятия ошибочных решений P _ош = 0,165.