Определение изменения формы поверхности непрерывно-неоднородного термоупругого полупространства при локальном нагреве

Введение. Учёт неоднородности свойств материала при моделировании тепломеханического воздействия является актуальной задачей термоупругости. Такая задача возникает, например, при исследовании свойств защитных покрытий из функционально-градиентных материалов для частей машин и механизмов, подвергающихся интенсивному тепломеханическому воздействию.

Подробное изложение основ термоупругости представлено в монографиях В. Новацкого [1] и А. Д. Коваленко [2]. Среди тех, кто активно занимается решением контактных термоупругих задач для однородных тел, стоит отметить Дж. Р. Барбера. В его работе [3] приводятся аналитические и численные методы решения задачи термоупругой устойчивости, а также приводятся результаты по изучению термоупругих деформаций.

В последнее время в отечественной и зарубежной научной литературе наблюдается растущий интерес к решению задач термоупругости для неоднородных материалов. Для задачи теп- лопроводности решения для отдельных видов законов неоднородности (экспоненциальный, линейный законы) приведены в работе [4]. Задача для слоистого покрытия решается в работе И. Г. Величко, И. Г. Ткаченко [5]. Собственный метод решения смешанных задач для экспоненциального закона неоднородности покрытия развивает N. Noda [6—7]. Решение плоской задачи для термоупругого взаимодействия в присутствии трения рассматривали также Liu, Ke, Wang [8].

Аналитические методы для решения термоупругих задач применяет Краснюк П. П. Так, в работе [9] рассмотрено решение плоской задачи контактного взаимодействия жёсткого теплопроводного штампа кругового поперечного сечения с упругим слоем.

Решения, используемые в приведённых выше работах, не могут быть применены для сложных случаев изменения термоупругих и механических свойств по глубине слоя.

В настоящей работе рассматривается осесимметричная квазистатическая задача термоупругости для функционально-градиентного полупространства, модуль упругости и коэффициенты Пуассона, теплопроводности и линейного расширения которого непрерывно изменяются в приповерхностном слое. Для её решения используется двусторонне-асимптотический метод, изложенный в статье [10].

Постановка задачи о воздействии локального источника с постоянной температурой на непрерывно-неоднородное полупространство. Рассмотрим полупространство Ω, термомеханические характеристики которого непрерывно меняются с глубиной в пределах прилегающего к поверхности слоя толщины H , а затем стабилизируются и остаются постоянными. С полупространством свяжем цилиндрическую систему координат ( r ,ф, z ) . При этом полагаем, что 0 <  r <^ , а z <  0. Обозначим через u,v,w смещения вдоль осей r , ф, z , а через σ _r ,σ_φ,σ _z ,τ _{r φ},τ _rz ,τ_{φ z} — радиальное, угловое, нормальное и тангенциальные напряжения соответственно. Кроме того, введём обозначения: для температуры — T , коэффициента теплопроводности — X_T ( z ) , коэффициента линейного расширения — a _T ( z ) , коэффициента теплоёмкости — c_T ( z ) . В ненапряжённом состоянии температуру полупространства примем равной T ₀ и будем анализировать разность температур 8 = T - T ₀.

На площадке 0 <  r <  а поддерживается постоянная температура и образуется тепловой поток, направленный внутрь неоднородного полупространства.

Далее будем полагать, что коэффициенты Ламе М ( z ) и Л ( z ) , коэффициенты теплопроводности X T ( z ) и линейного расширения a _T ( z ) являются непрерывными функциями координаты z , такими, что

• 1.    М ( z ) = М ( - H ) = М ⁵ , -»< z <- H Л ( z ) = Л ( - H | = Л ⁵ , Х т ( z ) = X т ( - H ) = X 5 , ^a т ( ^z ) = ^a т (^{- H} ) = ^{a 5} .

• 2.    М ( z ) = М C ( z ) , Л ( z ) = Л C ( z ) , - H <  z <  0                           (1)

• 3.    М C ( - H ) = М ⁵ , Л C ( - H ) = Л ⁵ ,

^X T ( ^z ) = ^X C ( ^z ) , ^a T ( ^z 1 = ^a C ( ^z ) .

X C ( - H ) = X T , a C ( - H ) = a 5 .

min Л ( z ) > Л . >  0, тахЛ ( z ) < Л* <* , z e ( -» ,0 )                          z e ( -» ,0 )

min М (z)> М, > 0, тахМ (z)< М*<», ze(-»,0) X                       ze(-»,0) X min XT (z)> X . > 0, maxXT (z)< XT<«, 2g(-№,0)                T           2g(-^,0)

min a _T ( z ) > a >  0, max a _T ( z ) < a _T , z e ( -» ,0 )                 '           z e ( -» ,0)

где H — толщина неоднородного слоя, сцепленного с подстилающим полупространством, то есть глубина, с которой мы полагаем термомеханические характеристики полупространства постоянными; индекс S соответствует подстилающему однородному полупространству; C — неоднородному слою; Л , , Л * , М * , М * , Л, Л*_Т , а^ . , а Т — произвольные константы.

Наряду с парой коэффициентов Ламе для описания упругого поведения твёрдого изотропного тела используются: модуль сдвига G и коэффициент Пуассона v или модуль Юнга E и коэффициент Пуассона v . Коэффициенты Ламе Л и М (иногда обозначаемый G и называемый модулем сдвига) связаны с модулем Юнга E , коэффициентом Пуассона v и изотермическим модулем объёмного расширения K соотношениями:

E Л =     Ev      E = М (2М + 3Л)

2(1 + v),     (1 + v)(1 - 2v),         М + Л , v 2(М + Л),(2)

3K ( z ) = 3Л ( z ) + 2М ( z ) .

Граничные условия, при сделанных предположениях, имеют вид:

[6 = 00,    r < a, z = 0, T zr = T z ф = 0, [56(3)

— o, I >  a .

la z

На границе сцепления неоднородного слоя с однородным полупространством, при z — - H , в силу непрерывности, должны выполняться условия сопряжения по смещениям, их производным, температуре и тепловому потоку:

оz (г, -H) — оS (г, -H), тCz (r, -H) — тz (r, -H), uC (r, -H) — uS (r, -H), wC (r, -H) — wS (r, -H),                            (4)

6 C ( r , - H ) — 6 S ( r , - H ) , ( 6 C ) ‘ ( r , - H ) — ( 6 S ) ‘ ( r , - H ) .

На бесконечности при (r,-H)r^ смещения, деформации и напряжения исчезают. Значения разности температур и теплового потока при этом также стремятся к нулю:

Jim ^ U ^{, w} ,Е r ,Е ф ,Е z ,£ rz ^,о _г ^,0 ф ,⁰ z ^,т z ^,6,6 ' ) ^— 0, l im( ^{u , w} ,£ r ,Е ф ,Е z ,£ rz ^,о r ^,0 ф ,⁰ z ^,T rz ^,6,6 ' ) ^— 0.

Требуется определить смещение поверхности покрытия:

d 6 d z

z — 0

— e ( r ) , r <  a .

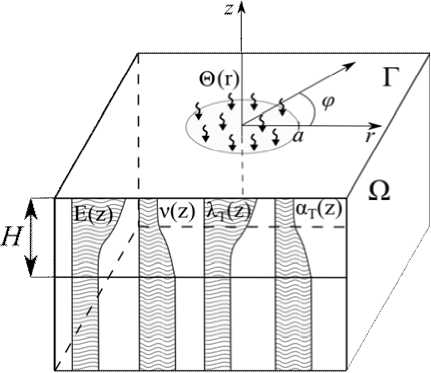
Рис. 1. Постановка задачи об изменении формы поверхности непрерывно-неоднородного термоупругого полупространства при локальном нагреве

Построение решения несмешанной задачи о термическом воздействии на непрерывно-неоднородное полупространство. При сделанных предположениях соответствующая краевая задача статической осесимметричной термоупругости в форме Ламе имеет следующий вид (без учёта кручения):

^.—,2     U ^                  W E         \^ WW W u ^        5 0

^{M (} z )^ 2 u - rT J + ( ^{M ( z ) + Л ( z} ) )_W r ^{+ M}'^{( z+} ^z J = k ^{( z)} _W r-

^M ( z ^{) v} 2 w ₊ ( ^M ( z ) + ^л ( z ^Ц ₊ ^2M ‘⁽ z ^{) W} ₊ Л ' ( z ) ^Е = k ⁽ z ) ⁰ ₊ k ⁽ z^          (7)

A t ( z ) V ² 0 + A T ( z ) 0 ’ = 0.

Здесь используются следующие обозначения:

M ‘ ( z ) =

d M ( z )

W u

dz

u

. .    d Л ( z )      ,

, Л ‘ ( z ) = —^, V ² dz

W w

Е =-- 11-- ,

W r   r    W z

_Л , z = d ^ T I z

^{T (} ) dz

1 W Г W )   W ²

= r +r, r W r ( W r J W z ²

dk z , k ( z ) = —^ dz

.

Будем искать решение для смещений u , w и температуры θ в виде интегралов Ханкеля:

to

to

u ( r , z ) = - J U ( Y, z ) J 1 ( Y r ) Y d Y, w ( r , z ) = j W ( /, z ) J о ( Y r ) Y d Y,

to

0 ( r , z ) = J T ( y, z ) J о ( Y r ) Y d Y.

Подставим (8) в систему дифференциальных уравнений в частных производных (7) и, приравняв к нулю подынтегральные выражения, получим систему обыкновенных дифференциальных уравнений второго порядка:

M U " + Y ( M + Л ) W ‘- Y ² ( 2M + Л ) U + M ‘ U ' + yM ' W = k/T , ( 2M + Л ) W" - / ( M + Л ) U' - Y 2 M W + ( 2M ' + Л ' ) W ' - YЛ ' U = kT + kT ',

AC (TC)"- y2XCTC +(XC )(TC )'= 0, где ’ указывает на дифференцирование по z .

Граничные условия (3) примут следующий вид (для общности мы учитываем также возможность приложения в пределах круга радиуса а горизонтального воздействия q ( r ) ):

T ' ( y ,0 ) = - B ( Y ) ,

В ( y ) = J в ( P ) J о ( PY ) Pdp.

Используя векторное представление для трансформант:

XT =( X1, x 2, x 3, x 4, x 5, x 6 ), x1 = U, x2 = U, x3 = W, x4 = W', x5 = T, x6 = T', запишем систему (9) в матричном виде, при этом явно выделим части соответствующие покрытию и подложке:

d x ^C

— = A C x C, dz dxS

— = A S x S , dz

- H <  z <  0,

- to <  z < - H ,

Граничные условия при этом имеют вид:

xC (Y,0 ) = -B (У), xC (y,0) = xS (y, -H), x3C (Y,0) = x3S (Y, -H), xC (Y,0) = x5 (Y, —H), xC (Y,0) = x5 (Y, —H),                          (14)

x C ( Y,0 ) = x 5 ( Y, — H ) , x C ( Y,0 ) = x 6 ( Y, — H ) .

Необходимо отметить, что последнее условие имеет место в силу непрерывности изменения свойств слоя и основания (4).

Общее решение системы (9) для однородного полупространства Л' = М ' = K ' = A T = О,

М >  О, Л >  О, K >  О, A T >  О имеет вид:

xS (y,z) = (di + yzd2 +(-K2/Y + (k2 + K3)z)d3) eYz, x5 (y,z) = (di +(1 + yz)d2 +(кзЛ + (K2 + K3)z)d3) YeYz, x35 (y,z) = (di +(-Ki + yz)d2 +(-K3/Y + (K2 + K3)z)d3)eYz,(15)

x5 (y,z) = (di +(1 - Ki + yz)d2 + (^/у + (k2 + K3)z)d3) YeYz, x5 (y, z) = d3eYz, x6 (y, z) = Yd3eYz,

Л + 3М         кк

K =, k, =             , k, =

• 1    Л + М 2 4 (2М + Л)

где d i ( i = 1,2,3 ) — произвольная функция параметра у .

Решение xC (у, z) системы дифференциальных уравнений (12) строится методом модули рующих функций. Будем искать xC (у,z) в виде:

xC (Y, z ) = E di (Y) a,- (Y, z) eYz.(16)

i = 1

Векторы a , ( y, z ) , ( i = 1,2,3 ) определяются из решения следующей задачи Коши:

dai = ACa, - ya,., - H < z < О, i = 1,2,3,(17)

dz i i при начальных условиях, для z = -H :

^a i ( У, ^z )| z =- h = ( 1,УД,У,⁰,⁰ ) ,

• ^a 2 ( Y, ^z ) I z =- H = ( Y z , Y ⁺ Y ^{2 z} , ^{- K} 1 ⁺ Y z , У ^{- K} 1 Y ⁺ Y 2 ^z , 0,0)| _z =_ _H -

• a3 (Y, z) I z =-H = (- K2 /У + (K2 + K3 ) z, K3 + (K2 + K3 ) Yz, -K3/Y + (K2 + K3 ) z, K2 + (K2 + K3 ) Yz, 1, Y)|z=_H "

Константы d i ( y ) ( i = 1,2,3 ) определяются из условия (14).

Таким образом, мы имеем

]T d i ( У ) O i ( У ) = - B ( У ) ,

M i ( У ) = М ( О ) a i ( У,О ) + М ( О ) ya³ ( у,О ) ,                               (18)

N i ( у ) = - Л ( О ) ya i ( у, О ) + ( Л ( О ) + 2М ( О ) ) а ^ ( у, О ) - к ( О ) а³ ( у,О ) ,

• о , ( У ) = a i ( У,О ) , O i ( у ) = O 2 ( У ) = О, где a i ( у, z ) , ( i = 1,2,3 ) обозначает k -ю компоненту вектора a i ( у, z ) , i = 1,2,3, к = 1,2,3,4,5,6.

  ^k 3 ( Y ) =

  
  

  d i =- ^k i3 ( Y ) B ( У ) , d 2 = ^k 2 ( Y ) B ( Y ) , d 3 = ^{- k} 3 B ( Y ) .

  
  

  k ( Y ) = ^k l ( Y ) =

  
  

  ^Д 23 ( Y )    1

  △ 12 ( Y ) 0 3 ( Y ) ,

  • △ 13 ( Y )    1

  • △ 12 ( Y ) O 3 ( Y ) ,

  
  

  O^ ) , △ , ( Y ) = N ( Y ) M , ( у ) - N , ( Y ) M ( Y ) .

  
  
  
  

  Окончательно получаем следующее выражение для компонент вектора решения x C ( у, z ) , при

  
  

  z > - H :

  
  

  L ( Y, z )

  
  

  X 1 = U ( y, z ) = ( L 3 ( Y, z ) B ( Y ) ) e ^{Y z} /y, x 2 = U'( y, z ) = ( L ( Y, z ) B ( Y ) ) e ^{Y z} /y, x з = W ( y, z ) = ( L 3 ( Y, z ) B ( Y ) ) e ^{Y z} /у , x 4 = W ' ( y, z ) = ( L ( Y, z ) B ( Y ) ) e ^{Y z} /y, x 5 = T ( y, z ) = L ( Y, z ) B ( Y ) e ^{Y z} /y, x 6 = T ' ( y, z ) = L ( y, z ) B ( y ) e ^{Y z} /у , Г                                          a i y. z\ )

  = ^k 13 ( Y ) ^a 2 ( Y, ^z )^{- k} 23 ( Y ) a 1 ( Y, ^z " J_{( y )}

  
  
  
  

  γ.

  
  

Введём обозначения:

да

1 3 ( r, z ) = J L ( Y, z ) B ( Y ) e ^Y J i ( Y r ) d y, ( k = 1,2 i = 1 ) , ( k = 3,4,5,6 i = 0 ) ,

да

J ki ( r , z ) = J L ( Y, z ) B ( Y ) e ^Y J ( Y r ) Y d y, ( k = 2 i = 0 ) , ( k = 4 i = 1 ) .

В соответствии с (8), (16) мы можем теперь выписать выражения для смещений, температуры, теплового потока и деформаций.

u ( ^r , ^z ) = I 311 ( ^r , ^z ) ^,w ( ^r , ^z ) = I 330 ( ^r , ^z ) , 6 ( ^r , ^z ) = I 350 ( ^r , ^z ) , ^{dQ (} _d z z ) = I 360 ( ^r , ^z ) .

Построение замкнутого приближённого численно-аналитического решения смешанной задачи статической теплопроводности о нагреве неоднородного полупространства источником с постоянной температурой в пределах круга радиуса a. Рассмотрим задачу о нагревании функционально-градиентного полупространства с поверхности источником с постоянной температурой в пределах круга радиуса a. Из (21)—(22) следует, что да

9 (r, z) = J L3 (у, z) B (у) J0 (Yr) eYzdy.(23)

На основании (3), (23) получаем, при z = 0: да

JL3 (у,0)B (у) J0 (yr)eYzdу = 90, r < a,(24)

где θ0 — температура источника тепла, а да e (r) = J B (a) J 0 (ra) ad a, B (у) = J в (p) J0 (Yp) pdp.(25)

Сделаем замену переменных и обозначим:

YH = u; X = H/a ; r ' = r/a ; p ' = p/ a ; L 5 ' ( y ) = L ( Y,0 ) , ^ ( p ' a ) = в ( p ) ,             (26)

далее штрихи опускаем. Получим, что поставленная задача сводится к решению интегрального уравнения вида:

1                      да

J в ( p ) p ^ p j L 5 ( u X ) J 0 ( ur X ^{— 1} ) J 0 ( upX ^{— 1} ) du = 0 0 , r <  1.

Выражение (27) представим в виде парного интегрального уравнения:

да

J B ( Y ) L ( Y, z ) J 0 ( Y r ) e ^Y z d Y = 0, r <  1,

< 0

1 да

J B ( Y ) J 0 ( r Y ) Y d Y = 0, r >  1.

. 0

Используя операторы

, , _x d tr Ф ( r ) dr     _t x

U ф ( ^r ) = -^ J гт^ ; ^UJ 0 ( ^r y ) = cos t y; ^{u 1} = 1; dt 0 tt — r

U t ф ( r ) = J r^ ( r ^ dr ; U t J 0 ( r Y ) = Y ^{— 1} cos t Y, 0 rr ² — t ²

преобразуем (28) к следующему виду:

да

J B (Y) L5 (Xy) cos (tY) dY = 1, t < 1, да

J B ( Y ) cos ( t Y ) d Y = 0, t >  1.

. 0

Аналогично работе [11] можно исследовать асимптотические свойства функции L ( u ) и показать, что её можно аппроксимировать выражением вида [12—13]:

L ( u ) = L N ( u ) + L ? ( u ) .

Здесь обозначено

N 2     2               M

L N ( u ) = П u^ + A h , L M ( u ) = I .

i = 1 u + B i             k = 1 u + D k

Рассмотрим простейший случай, когда L 5 ( u ) имеет вид:

5П.А- Y² + A ²X^—2

L ^{3 ( Y} ) Y ² + B 2 X ^{— 2.}

Тогда уравнение (31) для случая, когда область внутри круга некоторого радиуса нагревается источником тепла с постоянной по времени температурой, можно записать в виде:

да \/2    ^2 x — 2

f B ( Y ) ^Y—-7-7 cos tYd Y = 1, t <  1, 0 ^v ' y² + B ² X ^{— 2}

J B ( y ) cos tYd y = 0, t >  1.

. 0

Введём обозначение да в (t) = J B ( y ) cos tYdy .

Из уравнения (32) с учётом чётности правой части получим:

R 2 X — 2

в t = С ch AX ^{— 1}t + B ^.

⁽ )                   A ²X^{— 2}

Используя (33), (32) можно переписать:

j                                     R2 \-2

J B ⁽ Y ) cos tYd Y = C ch ^А^ + _{А К} , t ^ 1, j B ( y ) cos tYd Y = 0, t >  1.

. 0

Обращая преобразование Фурье, имеем:

x 2 B ² X ² sin u 2u u sin u ch А ¹ + A¹ cos u sh A ¹

B ( u ) = —-— ---+ C-------— --------

^Y n А²К ² u n             u ² + A²К

Постоянную С определим из условия, что B ( u ) должно удовлетворять исходному уравнению

(13). Получим:

C B К ^{- 1} ch А К ^{- 1} + А К ^{- 1} sh А К ^{- 1}    B К ^{- 1}

B ²К^{- 2} - А ²К^{- 2        +} А ²К^{- 2}

Формулу для теплового потока (25) приведём к более удобному виду, используя равенство Пар- севаля:

^в ( r ) = п

J 1       1

1 L (о) u r

+ C

ch А К ^{- 1}

V1 - r r

-11sh АК-1tdt АК I —, r V t2 - r2

Определение формы изменения поверхности неоднородного полупространства, нагретого источником с постоянной температурой в пределах круга радиуса a . Проанализируем деформацию поверхности неоднородного полупространства под действием локального статического нагрева. Согласно (23) при отсутствии поверхностного механического воздействия получаем:

a            j

W t ( r , z ) = J P ( p ) p d p J L 3 ( Y, z ) J о ( YP ) J о ( Y r ) e ^{Y z}d y .

В случае однородного полупространства формула (38) позволяет записать простые аналитические выражения для описания вертикального смещения поверхности полупространства при действии постоянного теплового потока и постоянной температуры. Рассматривается установившийся процесс подвода тепла к полупространству при отсутствии его отвода через поверхность, поэтому форма поверхности описывается логарифмической функцией и, для определённости, будем фиксировать некоторое значение r0 на оси r, при котором wt (r0,0) = 0 . При отображении получен- ных значений для перемещений поверхности на рисунке 2 примем r0 = 3,6.

1      1

wt (r) = wt (r,0) - wt (r0,0) = JJ0 (YP)PdPj-(J0 (Yr) - Jо (Yro))dY = 0-^1 - P jj

= J 4( J 0 ( Y r ) ^- J 0 ( Y ^r 0 ) ) sin Y d Y = J A( J 0 ( Y r )^{- 1} + ^{1 -} J 0 ("T ) ) ^sinY d Y =

0γ ln r0 + V1 - r2 - In1 + ^1   —, r < 1,

J 2                           2       ,, lnr0,   r > 1.

I r

На рисунке 2 представлено относительное изменение формы поверхности неоднородного полупространства под действием постоянной температуры, приложенной в пределах круга единичного радиуса. Обозначения кривых формируются следующим образом. Последовательно описывается характер изменения модуля Юнга, коэффициента Пуассона, коэффициента теплопроводности и коэффициента линейного расширения в покрытии:

• 0    — значение характеристики в покрытии не отличаются от соответствующих значений в подложке;

• 3    — значение характеристики на поверхности в 2 раза превышает значение в подложке и линейно убывает по всей толщине покрытия до значения в подложке;

• 4    — значение характеристики на поверхности в 2 раза меньше значения в подложке и линейно возрастает по всей толщине покрытия до значения в подложке.

Таким образом, обозначение 0_0_0_0 соответствует однородному термоупругому полупространству.

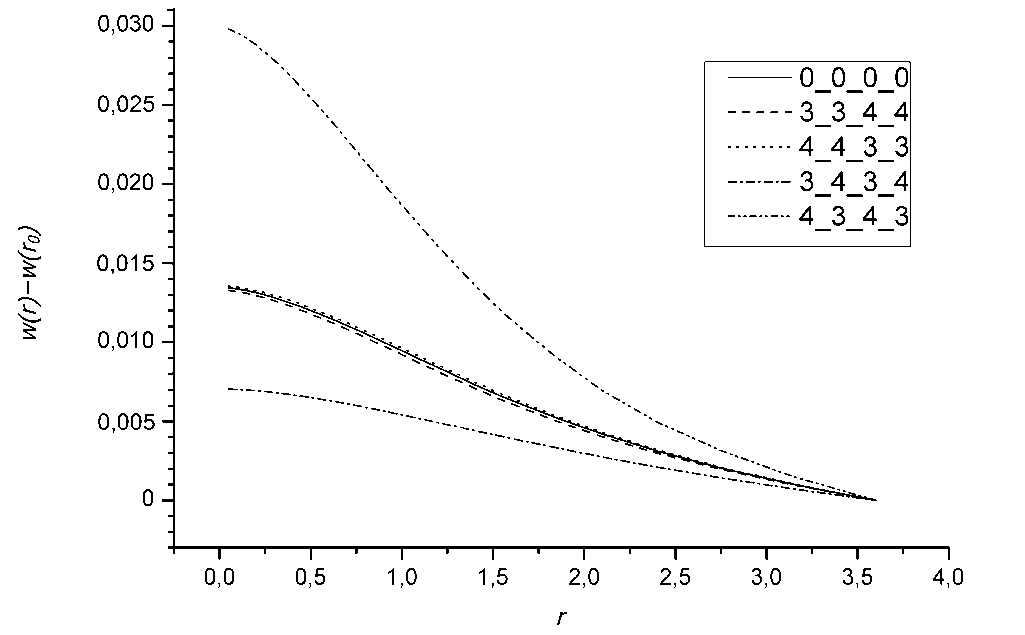
Рис. 2. Термоупругое искривление поверхности неоднородного полупространства для различных случаев изменения свойств в приповерхностном слое под действием равномерной температуры в пределах единичного круга. Толщина слоя равна радиусу круга

Анализ графиков на рисунке 2 показывает, что наибольшее влияние на величину максимального выпора поверхности оказывает разнонаправленное изменение коэффициентов теплопроводности и линейного расширения в покрытии.

Заключение. С помощью двусторонне-асимптотического метода построено решение задачи о локальном нагреве поверхности непрерывно неоднородного термоупругого пространство. Определены численные значения выпора поверхности при различном характере изменения упругих и термомеханических характеристик приповерхностного слоя. Показано, что характер неоднородности приповерхностного слоя оказывает существенное влияние на величину выпора поверхности. Библиографический список

• 1.    Новацкий, В. Теория упругости / В. Новацкий. — Mосква : Мир, 1975. — 863 с.

• 2.    Коваленко, А. Д. Введение в термоупругость / А. Д. Коваленко. — Киев : Наукова думка, 1965. — 204 с.

• 3.    Barber, J. R. Thermoelasticity and contact / J. R. Barber. // Journal of Thermal Stresses. — 1999. — Т. 22, № 4. — С. 513–525.

• 4.    Карташов, Э. М. Аналитические методы в теории теплопроводности твёрдых тел / Э. М. Карташов. — Москва : Высшая школа, 2001. — 550 с.

• 5.    Величко, И. Г. Аналитическое решение осесимметрической задачи термоупругости для многослойного основания [Электрон. ресурс] / И. Г. Величко, И. Г. Ткаченко // Вестник Восточно-укр. национ. ун-та им. В. Даля. — 2009. — № 4Е. — Режим доступа : http://www.nbuv.gov.ua/e-journals/Vsunud/2009-4E/09vigdmo.htm .

• 6.    Noda, N. On a general treatise of three-dimensional thermoelastic problems in transversely isotropic bodies / N. Noda, Y. Takeuti, Y. Sugano. // ZAMM Z. angew. Math. Mech. — 1985. — Т. 65, № 10. — С. 509–512.

• 7.    Jin, Z. H. Transient thermal stress intensity factors for a crack in semi-infinite plate of a functionally gradient material / Z. H. Jin, N. Noda. // International Journal of Solids and Structures. — 1994. — Т. 31, вып. 2. — С. 203–218.

• 8.    Liu, J. Thermoelastic contact analysis of functionally graded materials with properties varying exponentially / J. Liu, L. L. Ke, Y. S. Wang // Advanced Materials Research. — 2011. — Т. 189–193. — С. 988–992.

• 9.    Краснюк, П. П. Плоская контактная задача взаимодействия жёсткого теплопроводного цилиндрического штампа и упругого слоя при нестационарном фрикционном тепловыделении / П. П. Краснюк. // Трение и износ. — 2009. — Т. 30, № 2. — С. 152–162.

• 10.    Айзикович, С. М. Асимптотические решения контактных задач теории упругости для неоднородных по глубине сред / С. М. Айзикович // Прикладная математика и механика. — 1982. — Т. 46, № 1. — С. 148–158.

• 11.    Айзикович, С. М. О свойствах функций податливости, соответствующих слоистому и непрерывно-неоднородному полупространству / С. М. Айзикович, В. М. Александров // Доклады АН СССР. — 1982. — Т. 266, № 1. — С. 40–43.

• 12.    Айзикович, С. М. Осесимметрическая задача о вдавливании круглого штампа в упругое, неоднородное по глубине полупространство / С. М. Айзикович, В. М. Александров // Известия АН СССР, МТТ. — 1984. — Т. 39, № 2. — С. 73–82.

• 13.    Айзикович, С. М. Асимптотическое решение одного класса парных уравнений / С. М. Айзикович // Прикладная математика и механика. — 1990. — Т. 54, № 5. — С. 872–877.

Материал поступил в редакцию 14.02.13.