Определение эффективных упругих свойств поликристаллов методом вычислительного эксперимента

Даже однофазный поликристалл в силу анизотропии упругих свойств и различной ориентации главных осей симметрии материала отдельных кристаллитов является структурно-неоднородным материалом. В математических моделях при исследовании напряженно-деформированного состояния (НДС) различных конструкций и деталей, как правило, поликристалл заменяется модельным однородным материалом с эффективными упругими свойствами, упругое поведение которого эквивалентно заменяемому неоднородному материалу [4]. Эквивалентность здесь подразумевает одинаковую деформацию (в среднем) образцов из поликристалла и модельного однородного материала при одинаковом нагружении. При этом размеры образца должны быть не менее размеров представительного объема для поликристалла.

Использование на макроуровне (масштаб конструкции) однородного материала существенно упрощает применение традиционных вычислительных процедур (например, метода конечных элементов), исключая необходимость привязывать шаг расчетной сетки к размерам зерна. На мезоуровне (масштаб зерна) даже для однофазных поликристаллов из-за наличия анизотропии упругих свойств зерен и различной ориентации главных осей материала в них поля напряжений ст и деформаций е в кристаллитах будут неоднородными. В этом случае напряжения и деформации обычно раскладывают на средние и осциллирующие составляющие [4]:

СТ = < СТ > + ст' , £ = <  Е > + 8'.

При этом для средних и осциллирующих составляющих выполняются следующие условия:

J о' dV - 0, J8' dV - 0,(1)

VV

(0 -1 JОdV, ^ -1 J8dV,(2)

VVV где V- представительный объем поликристалла.

Напряжения ст и деформации 8 относятся к масштабному уровню зерна поликристалла (мезоуровень), а средние напряжения <ст> и деформации <8> будут соответствовать напряжениям 2 и деформациям £ на уровне конструкции (макроуровень), обычно измеряемым в эксперименте (Х=< о >, 8 =< 8 >). Размер представительного объема V за висит от размера структурных элементов (зерен) и от степени анизотропии их упругих свойств, количественной мерой которой является параметр анизотропии материала монокристалла [4]

A -

С -С

1111   '"1122

2С 1212

где Сц 11 , Сц₂₂ и С₁₂₁₂ - компоненты тензора модулей упругости кристалла с кубической решеткой в главных осях материала. Для материала с изотропными свойствами параметр анизотропии равен единице. Среди металлов только кристалл вольфрама имеет практически изотропные упругие свойства. Учитывая, что для материала с изотропными свойствами С ₁ ^и ₂ ^з ₁₂ - ( С _Ш1 - С ₁₂₁₂)/2, получаем

A -

из C 1212

с т.е. параметр анизотропии характеризует отклонение от изотропии упругих свойств через отношение модулей сдвига.

В работе [1] в результате решения краевой задачи были исследованы статистические характеристики полей мезонапряжений ст в однофазных поликристаллах. Анализ полученных результатов показал, что с уровнем значимости не менее 90 % мезонапряжения подчиняются нормальному закону распределения. На основании исследования корреляционной зависимости было установлено, что на расстоянии 4-5 средних диаметров зерна для алюминия и 6-7 средних диаметров для меди

НДС практически нескоррелированно. Полученные результаты для корреляции близки к экспериментальным данным исследования НДС в поликристаллах, полученных в работе [2]. В литературе [2, 4] размер представительного объема однофазного поликристалла при упругом нагружении рекомендуется принимать не менее 10 средних диаметров зерена.

С учетом формул (1) и (2) обобщенный закон Гука для макроуровня можно записать с использованием эффективных характеристик

а) S = С ^эф : г или б) б = S ^эф : S ,                  (3)

где С^эф - тензор эффективных модулей упругости; S³ * - тензор эффективных модулей податливости ( S ^эф = ( С ^эф ) ^-1 ). Таким образом, эффективные модули упругости связывают осредненные по представительному объему мезонапряжения и мезодеформации.

Тензорные соотношения (3) можно представить в матричной форме:

{ S } = [ C ^ф ]{ е } или { е } = [ 5 ° ^ф]{ 2 }.                  (4)

В данном случае для симметричных тензоров S и е переход к матричной записи (4) осуществляется аналогично [4]. В результате подобного перехода для описания упругих свойств материала получаем симметричные матрицы [ 5 °^ф ] и [ C ^ф ] размером 6 на 6 элементов. Требование симметрии матриц упругих свойств справедливо для всех материалов, для которых выполняется допущение о существовании упругого потенциала [4].

На практике кроме модулей упругости и податливости для описания упругих свойств материала часто используют так называемые технические постоянные: модули Юнга E , коэффициенты Пуассона ц , модули сдвига G , а также коэффициенты взаимного влияния. В табл. 1 приведена запись компонент матрицы модулей податливости через технические упругие константы материала.

Таблица 1

Связь модулей податливости S jl и технических констант

ij \ kl	11	22	33	12	23	13
11	1/ E 1111	- ц 1122 / E 2222	- ц 1133 / E 3333	V 11,12 / G 1212	V 11,23 / G 2323	V 11,13 / G 1313
22	- Ц 2211 / E 1111	1/ E 2222	- Ц 2233 / E 3333	V 22,12 / G 1212	V 22,23 /G 2323	V 22,13 / G 1313
33	- Ц 3311 / E 1111	- Ц 3322 / E 2222	1/ E 3333	V 33,12 / G 1212	V 33,23 / G 2323	V 33,13 / G 1313
12	V 12.11 / E 1111	V 12,22 / E 2222	V 12,33 / E 3333	1/ G 1212	Л 12,23 / G 2323	Л 12,13 / G 1313
23	V 23.11 / E 1111	V 23,22 / E 2222	V 23,33 / E 3333	Д 23,12 / G 1212	1/ G 2323	Л 23,13 / G 1313
13	V 13,11 / E 1111	V 13,22 / E 2222	V 13,33 / E 3333	Л 13,12 / G 1212	Л 13,23 / G 2323	1/ G 1313

Как можно видеть, технических констант в общем случае получается 36, так как, хотя матрица модулей податливости симметрична ( S ij _nm= S nmij ), соответствующие коэффициенты влияния не равны друг другу (например, р_П 22 * Ц 2211 ).

Экспериментально упругие свойства материала определяют как в опытах на простое нагружение (растяжение, сжатие, сдвиг, изгиб), так и с помощью измерения и анализа распространения звуковых волн. В вычислительных экспериментах для определения упругих свойств предпочтительнее использовать первый подход.

Рассмотрим определение эффективных модулей податливости [ 5 °^ф] материала с помощью серии вычислительных экспериментов на статическое («мягкое») нагружение представительного объема однородной нагрузкой (рис. 1). По физическому смыслу модуль податливости соответствует деформации материала при единичном напряжении. Осуществим одноосное растяжение материала вдоль оси X ₁ единичной нагрузкой ( 5 11 = 1, 5 ₂₂ = 5 ₃₃ = 5 ₁₂ = 5 ₂₃ = 5 ₁₃ = 0, рис. 1) и определим возникающие при этом средние деформации <е>. Из выражения (3, б ) получаем 6 эффективных модулей податливости.

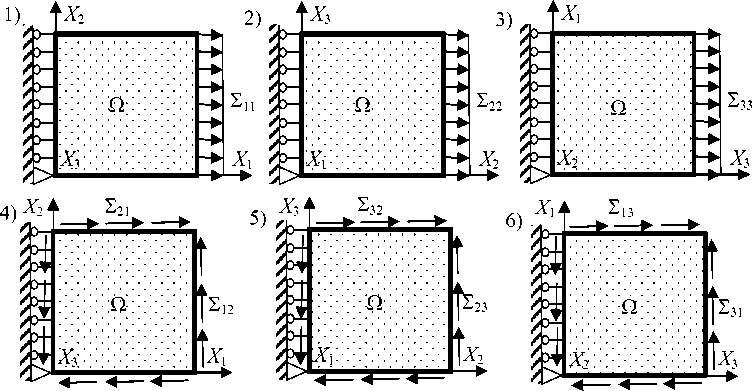
Рис. 1. Серия из 6 экспериментов по определению эффективных упругих свойств материала еэф _/<Л|=1     сэф -/ cz11 =1     сэф -/ Pz11 =1

° 1111 < ° 11     >  ,    2211    <  ^ 22    >  ’ 3311 <  ^ 33    > ,

S ™ =< .•    > , S 2*1 =< тй^{1 - 1} > , s^ =< ;■     > .

С использованием соотношений табл. 1 получаем для технических констант:

F ^эф = 1/ <  р^е" ^{1       эф} = < р^Е" ¹ > Р^{эф эф} = < р^Е'' ¹ > F³*

^ ''        ^ ^ '1    ^ ,   Н 21 ^ ^ 22    ^ -^11 ,  Н 31 ^ ^ 33    ^   11 ,

V^эф __^E '1 I рз^    ^эф _   ^ I рз^ ^эф _ ^Е ', I    рз^

^V 12,1 “^ ( 12 ^ E ll , ^V 23,1 “^ ( 23 ^ E ll , ^V '3,1 “^ ( '3 ^ E ll •

В силу неоднородности и анизотропии свойств нагружаемого материала в общем случае все 6 оценок осредненных по объему компонент тензора деформаций не будут равны нулю.

Выполняя аналогичные эксперименты на растяжение вдоль осей X 2 и X 3 , а также простой сдвиг в плоскостях X , X 2 , X 2 X 3 и X , X 3 (см. рис. l), получаем 36 оценок эффективных модулей податливости:

	К=ЕГ')	/ с е22 °' \ \ ь11    /	/ у _1 \ / о Е33 °' \ \ ь11    /	/р Е12 °'\ \ b11 /	/ у„ -1\ / о е23 °' \ \ ^'1 /	/р Е'3 °' \~ \£''   /
	Е'1"^ \ ^22   /	/ о е 22 °' \ \ ь22   /	/ у _1 \ / о Е33 °' \ \ ь22 /	/р Е12 °'\ \ ь22   /	/ у„ -1\ / с е23 °' \ \ ъ22 /	L Е'3 ° ' \ ь22
	U Ell “1^ \ ^ 33 /	/ о Е22 °' \ \ ь33   /	/ Е„°'\ 33 \ ^ 33   /	/р Е12 °'\ \ ь33   /	/ Е..°'\ 23 \ ^ 33   /	/ Еп°1 13 \ ь33
[ S эф ] °	х 1 (уГ)	( У^ °')	/ Е-»-» °' \ \ У1233   /	Е 12°'\ \ (12 /	Е„ ° ' (у ,2 23   ;	/ Еп°1 \ У12 3
	/vEll °'\ ' У 23 /	( У Е3? °')	/ Е„ °' \ \ У 233 /	Е 12°'\ \ ( 23 /	Е„ ° ' (у 23   ;	/ Еп°1 \ У 23 3	\ /
	_(Й'"')	( Ув22 °')	Е„ ° , \У '3 33   /	Е 12°'\ \ (13    /	Е„ ° ' (У '3 23   ;	/ Еп°1 \ У '3 3

Аналогично можно провести серию экспериментов над представительным объемом по кинематическому («жесткому») нагружению, задавая перемещения границ. Макродеформации представительного объема в этом случае равны заданным, а макронапряжения получаем путем осреднения мезонапряжений. Проведя 6 экспериментов и получив 6 полей мезонапряжений, с использованием выражения (3, а ) получаем систему из 36 уравнений, решив которую можно найти 36 элементов матрицы модулей упругости [ С °^ф]. Оба подхода (на «мягкое» и «жесткое» нагружение) эквивалентны, хотя первый менее трудоемок, так как не требует решения системы из 36 уравнений.

Матрицы [Sф] и [Сф] в классической теории упругости являются симметричными, поэтому информация, полученная в 6 экспериментах, является избыточной. Однако как в натурном (в силу ошибки измерения), так и в вычислительном эксперименте (в силу конечности выборки и в силу ошибок округления) симметрия [5°ф] будет выполняться с некоторой погрешностью. Для удовлетворения симметрии [5°ф] можно потребовать выполнения следующих дополнительных условий:

Sij*m " 5Пlj ^ 5, У * nm, i,j, n, m = 1,2,3, где 5 - допустимая погрешность на симметрию, 5 > 0.

Нарушение симметрии [ 5 ^3ф] может свидетельствовать о недостаточной величине представительного объема, неоднородности макронагружения или статистической неоднородности полученной выборки мезодеформаций. Последнее может быть вызвано краевыми эффектами вблизи поверхности образца. Поэтому в вычислительном эксперименте из выборки мезодеформаций или мезонапряжений следует исключить приграничные области. Основываясь на принципе Сен-Венана, можно предположить, что размер моделируемого поликристалла должен по крайней мере в три раза превышать размер представительного объема.

Как правило, для любого материала (в том числе и модельного) можно найти главные оси симметрии, в которых число ненулевых компонент матрицы [ 5 ^ф ] минимально. Например, материал с ортотропным типом симметрии в главных осях имеет только 12 элементов [ 5 ^ф ], отличных от нуля. Причем из них в силу симметрии только 9 компонент будут независимыми.

Изложенные выше методики позволяют определять значения эффективных модулей упругости или податливости в некоторой лабораторной системе координат (ЛСК), привязанной к конструкции, процессу или образцу. В общем случае ориентация ЛСК может не совпадать с ориентаций главных осей получаемого модельного материала. Ориентация главных осей симметрии далеко не всегда очевидна. Например, в случае многофазного поликристалла или при образовании текстуры кристаллизации или деформационной текстуры определить ориентацию главных осей получаемого однородного модельного материала по форме и размерам зерен бывает затруднительно.

Пусть с помощью предложенных методик определены значения компонент тензора модулей упругости или податливости в ЛСК. Введем пространство Q , содержащее все возможные ориентации материала. Для определения главных осей симметрии материала требуется найти такую ориетацию to , где число ненулевых компонент тензора модулей упругости С ^ф минимально. Соответствующая задача оптимизации может быть записана следующим образом.

Найти ориентацию ю материала относительно ЛСК, доставляю щую

3 3 3 3 , ЪЪЪЪ H ( i =1 j =1 k =1 i =1 ^v

X-. ю

^C ijkl

. х meQ

- C ™ⁿ j ^ min,

при ограничениях типа равенств

СЮ ю ю Ю ю Сэф ijkl рinр jmрkpрlq nmpq, где H(x) - функция Хевисайда, H(x) = 1 при x > 0 и H(x) = 0 при x < 0; Сmin - минимально возможное отличное от нуля значение компоненты тензора модулей упругости, Сmin > 0; [рю] - матрица косинусов поворота из ЛСК к ориентации ю.

Очевидно, что точность изложенных подходов зависит от точности определения полей мезонапряжений и мезодеформаций в представительном объеме. Наиболее корректно это можно сделать, решив краевую задачу для представительного объема с учетом реальной геометрии и ориентации материала зерен, а также учитывая распределения фаз материала. При этом в процессе решения учитывается взаимодействие не только соседних, но и далеких друг от друга зерен поликристалла. К недостаткам подобного подхода следует отнести трудоемкость реализации метода, потребность в значительных вычислительных ресурсах и больших затратах машинного времени. Тем не менее методы прямого моделирования зачастую являются единственным средством исследования мезопараметров поликристалла. Кроме того, подобный подход может служить для обоснования гипотез и приближений, используемых для разработки более эффективных в вычислительном отношении методов.

Рассмотрим объем однофазного поликристалла в форме куба, размер которого более 10 средних размеров зерна. Математическая постановка краевой задачи для моделируемого объема выглядит следующим образом.

Требуется определить распределение полей мезоперемещений u, мезонапряжений о и мезодеформаций е в объеме V поликристалла с границей Г (V = V иГ), состоящим из N зерен объемом Vn (V = Ъ N.1 Vnj • Материал каждого зерна однороден и в общем случае имеет отличную от других зерен ориентацию главных осей симметрии материала. В каждой точке r зерна n НДС должно удовлетворять следующим соотношениям:

• -    уравнениям равновесия

V • о = 0 , V r е V_n ,

• -    определяющим соотношениям

ст = C : е, V r е V ,

• -    и геометрическим соотношениям

Е = 2 ( V u + V u T ) , V r e V n .

Граничные условия 6 экспериментов приведены на рис. 1.

В данной работе численная реализация экспериментов проводилась с использованием метода конечных элементов [3]. При этом каждое зерно области разбивалось на 6 симплекс-элементов в форме тетраэдра.

Оценка эффективных упругих свойств проводилась для однофазного поликристалла меди, модули упругости и технические константы монокристалла которой в главных осях симметрии имеют следующие значения:

C mi = 168,4 ГПа, C 1122 = 121,4 ГПа, C 1212 = G 1212 = 75,4 ГПа,

E 1111 = 66,7 ГПа, Щ122 = 0,419.

В поликристалле ориентацию ш главных осей симметрии материала отдельных зерен относительно ЛСК можно рассматривать как случайную величину. В этом случае, задавая ориентацию ш набором углов Эйлера { ф ₁, ф ₂, ф з }, можно величины последних рассматривать как случайные. В зависимости от закона распределения ориентаций зерен получается тот или иной вид текстуры поликристалла. При равномерном случайном законе распределения ориентаций текстура в поликристалле отсутствует, а эффективные упругие свойства должны быть близки к изотропным.

Исследование эффективных упругих свойств проводилось при разбиении объема V в форме куба на 15 зерен по стороне по выборкам из 3375 зерен. Полученные в результате 6 вычислительных экспериментов модули податливости приведены в табл. 2.

Таблица 2

Эффективные модули податливости [ S^ l х- 10 6 ]

ij \ kl	11	22	33	12	23	13
11	7,20	–2,33	–2,41	0,03	–0,01	–0,03
22	–2,33	7,18	–2,40	0,01	0,08	0,03
33	–2,44	–2,42	7,24	–0,04	–0,08	–0,01
12	0,03	0,01	–0,04	19,26	0,06	–0,04
23	–0,01	0,08	–0,07	0,06	19,26	–0,07
13	–0,03	0,02	–0,02	–0,04	–0,07	19,45

Как было отмечено, в вычислительном эксперименте симметрия матрицы упругих свойств выполняется приближенно. В данном случае незначительное нарушение симметрии наблюдается для модулей S 1^2 , S n33 и S 2Э ^ф зз . Эффективные модули податливости определяются по математическому ожиданию случайного поля компонент тензора мезодеформаций, оценка величины которого в данном случае с вероятностью 95 % принадлежит интервалу ± 0,08 - 10 ^-6 . С учетом последнего замечания можно заключить, что нарушения как симметрии, так и изотропии упругих свойств не выходят за границы интервала статистической погрешности. Соответствующие табл. 2 значения технических констант приведены в табл. 3.

Таблица 3

Технические константы материала E^ l , G jl , ц Э^ф , ^ эф и v эф

ij \ kl	11	22	33	12	23	13
11	140,1 ГПа	0,324	0,330	5	5	5
22	0,325	139,8 ГПа	0,331	5	5	5
33	0,337	0,337	139,3 ГПа	5	5	5
12	5	5	5	52,4 ГПа	5	5
23	5	5	5	5	52,6 ГПа	5
13	5	5	5	5	5	52,7 ГПа

Примечание: 5 - величины менее 0,01 по абсолютной величине.

С учетом интервалов статистической погрешности эф

E ^эф = 139,8 ± 1,5ГПа, ц^эф = 0,331 ± 0,007, G ^эф =------—.

2(1 + ц ^эф )

Для однофазных поликристаллов в работе [4] приведены упрощенные соотношения оценки упругих эффективных характеристик по Фойгту, Рейсу и Хиллу. Для меди данные оценки, а также результаты натурного и вычислительного экспериментов сведены в табл. 4.

Эффективные упругие свойства чистой меди

Таблица 4

Модули	Натурный эксперимент	По Рейсу	По Фойгту	По Хиллу	Вычислительный эксперимент
G эф, ГПа	44–48	40	55	47	52,5
E эф, ГПа	117–126	109	145	127	139,8
цэф	0,31–0,34	0,37	0,32	0,35	0,331

Результаты натурного эксперимента существенно зависят от чистоты и способа получения поликристаллической меди и имеют достаточно серьезный разброс. Сравнивая приведенные значения, можно заключить, что полученные при прямом моделировании результаты близки к значениям, наблюдаемым в натурном эксперименте, и расположены между приближением Хилла и Фойгта.

Применим приведенную выше методику для оценки эффективных упругих свойств для поликристалла при наличии аксиальной текстуры. Отсутствие текстуры достигается, если любое направление в кристаллической решетке равномерно распределено по пространству ориентаций Q . При этом углы Эйлера изменяются в следующих пределах

0 < ф1 < 2л, 0 < ф2 < л, 0 < ф3 < 2л, где ф1 задает поворот вокруг оси X3, ф2 - оси X1', ф3 - оси X3".

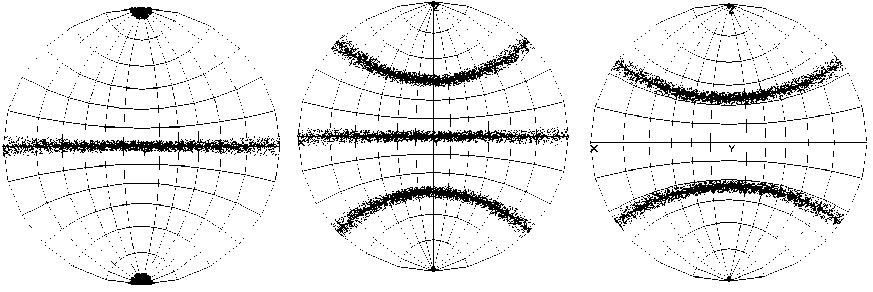
Пусть угол ф ₂ равномерно изменяется в интервалах [0; Аф ] и [ л - Аф ; л ]. В этом случае получаем аксиальную текстуру, когда направление [100] кубического кристалла равномерно заполняет телесный угол Аф вокруг оси X 3 ЛСК. Соответствующие прямые полюсные фигуры для случая Аф = 5 приведены на рис. 2.

В данном случае главные оси симметрии материала сопадают с ЛСК. В табл. 4 приведены величины эффективных технических констант поликристаллической меди при различных значениях интервала Аф .

[100]                         [110]                          [111]

а                          б                           в

Рис. 2. Прямые полюсные фигуры для аксиальной текстуры (направление [100] кубического кристалла вокруг оси X 3 , Аф = 5 )

Таблица 5

Технические константы меди с аксиальной текстурой

Аф, град	E 1111, ГПа	E 2222, ГПа	E 3333, Гпа	G 1212, ГПа	G 2323, ГПа	G 1313, ГПа	М- 1212	М- 2323	М 1313
90	139,8	139,8	139,8	52,5	52,5	52,5	0,331	0,331	0,331
75	142,1	142,1	145,6	52,5	50,6	50,6	0,334	0,322	0,322
60	139,5	139,5	139,5	53,1	48,7	48,7	0,341	0,325	0,325
45	134,1	134,1	127,2	51,7	52,5	52,5	0,312	0,345	0,345
30	124,9	124,9	101,7	48,6	61,6	61,6	0,236	0,375	0,375
15	109,3	109,3	77,3	47,9	71,3	71,3	0,159	0,406	0,406
5	102,5	102,5	67,6	47,5	75,0	75,0	0,117	0,418	0,418
0	103,7	103,7	66,7	47,2	75,4	75,4	0,097	0,419	0,419

Как видно из приведенных в табл. 5 результатов, данному типу текстуры соответствует материал с трансверсально-изотропными свойствами. Плоскость изотропии совпадает с плоскостью XX 2 ЛСК.

Следует отметить, что на интервале для Аф от 90 до 45 анизотропия упругих свойств поликристалла незначительна. Более того, при Аф = 45 поликристалл демонстрирует свойства, близкие к изотропным. В дальнейшем при стремлении Аф к 0 упругие свойства поликристалла в направлении оси X 3 стремятся к свойствам монокристалла.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (гранты РФФИ № 10-08-00156-а, № 10-08-96010-р_урал_а).