Определение касательных напряжений при малых числах Рейнольдса

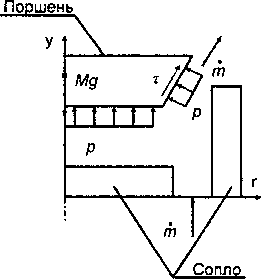
Предприятием ООО «Метран-СТАР» (г. Челябинск) выпускаются задатчики давления «Воздух-1600». Это эталоны давления первого разряда с классом точности 0,02, которые воспроизводят избыточные давления в диапазоне от 20 Па до 16 кПа. Принцип прибора состоит в преобразовании силовой характеристики поршня в давление (рис. 1). Наиболее интересующая область давлений от 20 Па до 1000 Па характеризуется малыми числами Рейнольдса. В данной работе поставлены следующие цели: определить на сколько точно можно проводить численный анализ течения газа при данных числах Re; проанализировать влияние состояния кромки на интеграль ную силу', воздействующую на поршень.

Таблица 1

р, Па	М- 103, кг	7Й-106, кг/с
279,50	13,9908	1,4
279,64	14,0080	1,4
: 279,90	14,0108	1,4
280,44	14,0408	1,4
281,47	14,0908	1,4
356,11	17,8154	2,8

Анализ исходных данных. При проведении физического эксперимента контролировались следующие характеристики: р - давление под поршнем, М- масса поршня, m - массовый расход газа, подаваемый в систему сопло-поршень, экспериментальные данные представлены в табл. 1.

При численном моделировании использовалось 3 вида граничных условий: 1 - твёрдая стенка, 2 - граница постоянного давления (атмосфера), 3 - граница постоянной скорости (подача газа в систему). Численный эксперимент состоит из 2-х частей: 1) по результатам предварительного эксперимента по нескольким точкам определяется конфигурация кромки со пла; 2) после определения кромки рассчитывается масса и сравнивается с экспериментальным значением. Максимальное число Рейнольдса для данного эксперимента равно:

„ Д-У-с

Re =----- м

m             2,8-10"⁶

р • D_o • м ~ 3,14-12,35 ■ 10'³ • 1,8 ■ 10"⁵

как показано в работе [2], это течение соответствует полностью ламинарному движению. Сжимаемость газа и теплоперенос от стенки не учитывается.

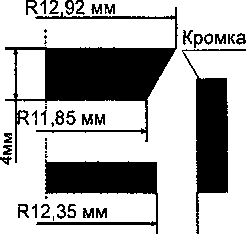
R12.5 мм

Рис. 2. Геометрия прибора

Рис. 1. Принципиальная схема прибора

Терёхин А.А., Сидельников Р.В., Определение касательных напряжений Рандина Т.В. при малых числах Рейнольдса

Основные уравнения и вычислительный метод. Вычислительный алгоритм основывается на методе контрольного объёма (МКО) [3]. Основная идея МКО состоит в разбиении расчётной области на контрольные непересекающееся объёмы, таким образом, что каждая узловая точка содержится в контрольном объёме. Дифференциальное уравнение интегрируется по каждому контрольному объёму. Одним из важных свойств МКО является то, что в нем заложено точное интегральное сохранение таких величин, как масса, количество движения и энергия на любой группе контрольных объемов и, следовательно, на всей расчетной области. Это свойство проявляется при любом числе узловых точек, а не только в предельном случае очень большого их числа. Решение на грубой сетке удовлетворяет точным интегральным балансам. В методе контрольного объема ищется решение в виде значений только в узловых точках. Интерполяционные формулы или профили рассматриваются как вспомогательные, необходимые для расчета интегралов

В качестве исходных уравнений используются уравнения Навье-Стокса для описания ламинарного движения вязкой несжимаемой ньютоновской жидкости при отсутствии массовых сил в векторно-тензорной форме [4]:

8«к । ». 8Uk 1 8Tjk = 1 9р

Р ОХк ’

МКО позволяет получить характеристики нестационарного течения газа, а также с помощью процесса установления, их стационарные значения для задач обтекания тел.

Результаты численного эксперимента. Численный эксперимент проводится в программе DinamLGTM, модернизированной для решения задач газовой динамики несжимаемой жидкости. Рассматривается двумерное осесимметричное обтекание при различном состоянии кромки, радиусы скругления которой принимают значения: 0,035 мм, 0,07 мм, 0,15 мм и кромка, образованная фаской (рис. 3,4).

Рис. 4. Конфигурация кромки, образованной фаской

Рис. 3. Конфигурация кромки, образованной радиусом

Общая интегральная сила, действующая на поршень, определялась как сумма касательных и нормальных. Данная сила уравновешивается весом поршня Mg, при ускорении свободного падения g = 9,8144 м/с². Погрешность численного вычисления определяется как разница между вычисленной интегральной силой, образованной вследствие воздействия газового потока и весом поршня, который известен из эксперимента. Погрешность определяется по формуле:

вдяьда].100%

Численный эксперимент проводится последовательными приближениями. Изменяя высоту всплытия поршня таким образом, что давление под поршнем достигает экспериментального при различных состояниях кромки.

Этап I. На рис. 5 показан характер изменения воздействующей силы газового потока в зависимости от давления под поршнем и состоянием кромки. Наименьшее отклонение от эксперимента показывает численный анализ при состоянии кромки состоящей из 2-х фасок (см. рис. 4). Максимальная погрешность вычислений при этом составляет 0,07% (рис. 6). Максимальное влияние касательных сил на интегральную силовую характеристику составляет 0,2% (рис. 8).

Серия «Машиностроение», выпуск 7 45

Расчет и конструирование

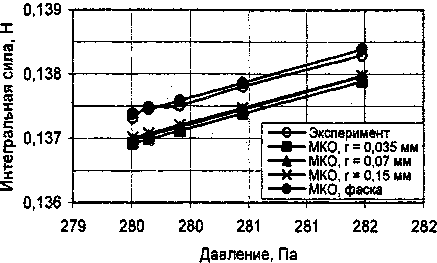
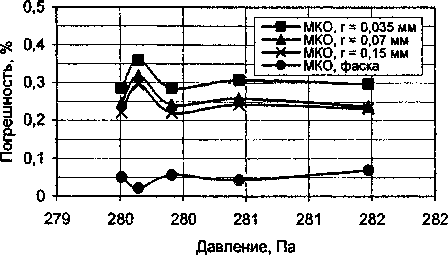
Рис. 5. Изменение интегральной силы                      Рис. 6. Изменение погрешности от давления                                 вычислений от давления

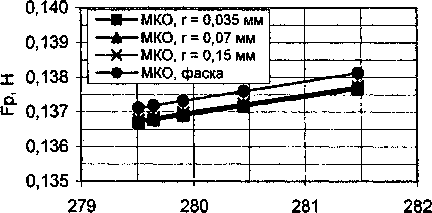
Рис. 7. Изменение нормальных сил от давления    ' Рис. 8. Изменение касательных силы от давления

' при различном состоянии кромки                  ■ при различном состоянии кромки

Этап II. После определения состояния кромки проводится прямое сравнение: задаются граничные условия согласно контрольной точки при р = 356 Па и сравнивается масса вычисленная и экспериментальная. Результаты приведены в табл. 2.

Численное моделирования играет значительную

Таблица 2

p, Па	Мэксп, г	Мчисл, г	Процент
356,11	17,8154	17,8456	0,17

роль для решения задач при малых давлениях, т.к. в этой области проведение анализа и построения методики затруднительно. Влияние различных геометрических параметров и сложная геометрическая форма не позволяют точно аналитически анализировать газовый процесс. Погрешность в 0,17% возникает за счет отличия реального состояния кромки от идеального (заложенного в программу через геометрию).

При точно известной геометрии расхождение можно значительно уменьшить. Возможность моделирования газового процесса в этой области позволит в дальнейшем дать предпосылки для разработки методов повышения точности прибора.

Данная работа проведена при финансовой поддержке ПГ «Метран».