Определение коэффициента интенсивности напряжений первого типа для двух коллинеарных трещин методом граничных элементов

В статье рассматривается случай совместного раскрытии двух коллинеарных трещин равной длины L, расположенных на расстоянии b друг от друга (рис. 1). Под действием внутреннего давления рвн в трещинах, деформированное состояние среды, описываемое непрерывными ана- литическими функциями, претерпевает разрывы в окрестностях рассматриваемых трещин. Смещение противолежащих берегов трещины относительно друг друга представляет собой разрыв смещений в данной точке при определении деформированного состояния среды.

Рис. 1. Расчетная схема

В рамках данной статьи рассматриваются два случая нагружения расчетной схемы (рис. 1), разделяющие исходную задачу на две подзадачи:

• 1)    Обе трещины нагружены давлением ^рвн ^;

• 2)    Давление р вн воздействует только на первую трещину (левую).

При проведении расчета приняты следующие значения исходных данных:

• 1)    Длина трещин L =[2; 5; 10]-10 " ³ м;

• 2)    Ширина промежутка между трещинами b =[0,5; 1; 2; 5]^10 " ³ м;

• 3)    Число граничных элементов на одной трещине N =10;

• 4)    Модуль Юнга E =30-10⁹ Па;

• 5)    Коэффициент Пуассона v =0,25;

• 6)    Внутреннее давление р вн =100^10⁶ Па.

Методика расчета

Для применения численного метода решения (метод граничных элементов) необходимо получить поэлементное разбиение исходных трещин на N элементов равной ширины Лх для определения величин раскрытий трещины D y (рис. 2).

Последующий численный расчет предполагает получение значений коэффициентов влияния, отражающих зависимость раскрытия определенного граничного элемента от раскрытия всех остальных. Данные коэффициенты являются аналогом модуля Юнга и отражают нормальное напряжение в i -ом элементе вызванное единичным перемещением в j -ом элементе. Подробное описание методики численного расчета разрывов смещений приведено в (1).

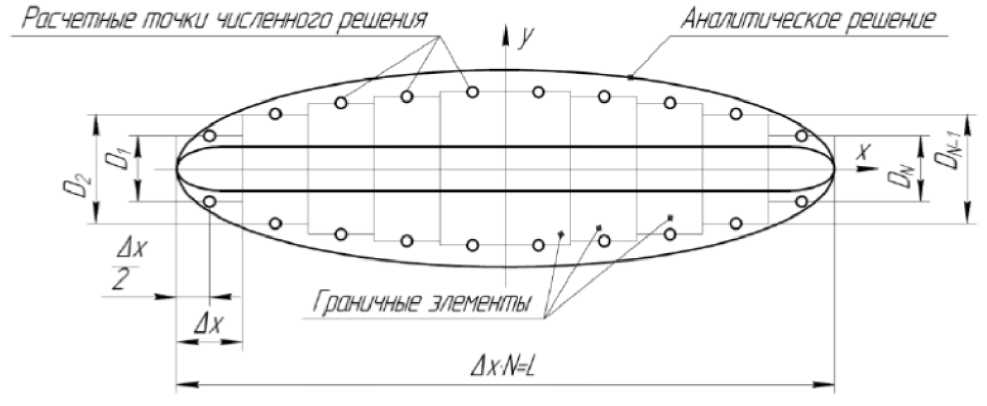
Рис. 2. Конечно-элементное разбиение исходной трещины

Расчет разрывов смещений

Определение разрывов смещений по заданному разбиению исходных трещин сводится к решению системы линейных

№№

• У -^ + £ 1=1i=1

№№

• У -TjD + У 1=1i=1

Результаты расчета для 1-ой и 2-ой подзадач приведены в таблицах 1 и 2, соответственно. При записи значений разрывов смещений знак «минус», характеризующий растяжение среды, условно опущен.

уравнений описывающих напряженно-деформированное состояние граничных элементов (1)

А^ Т = " S

A^lj D^j = л-i

⁴Tm^Dn   ° n

Исходя из соображений симметрии расчетной схемы (рис. 1) значения разрывов смещений по 1-ой подзадаче представлены для первых N граничных элементов (левая трещина).

Таблица 1. Разрывы смещений для случая нагружения обеих трещин

№ эл.	Разрыв смещений D n , мкм
	L =2 мм
	b =0,5 мм	b =1 мм	b =2 мм	b =5 мм
1	7,59	7,33	7,14	6,99
2	10,85	10,46	10,16	9,94
3	12,85	12,35	11,97	11,69
4	14,11	13,50	13,05	12,74
5	14,80	14,09	13,58	13,23
6	14,97	14,16	13,61	13,24
7	14,61	13,73	13,13	12,75
8	13,66	12,70	12,09	11,71
9	11,87	10,89	10,31	9,96
10	8,61	7,75	7,28	7,01
№ эл.	L =5 мм
	b =0,5 мм	b =1 мм	b =2 мм	b =5 мм
1	19,97	19,20	18,53	17,85
2	28,69	27,48	26,43	25,40
3	34,18	32,60	31,24	29,92
4	37,77	35,84	34,20	32,64
5	39,93	37,65	35,73	33,95
6	40,83	38,17	35,99	34,02
7	40,44	37,39	34,95	32,83
8	38,56	35,09	32,42	30,23
9	34,56	30,69	27,91	25,77
10	26,45	22,49	19,95	18,19
№ эл.	L =10 мм
	b =0,5 мм	b =1 мм	b =2 мм	b =5 мм
1	41,67	39,95	38,40	36,67
2	60,08	57,38	54,96	52,28
3	71,89	68,36	65,20	61,73
4	79,90	75,54	71,69	67,50
5	85,07	79,87	75,30	70,43
6	87,77	81,66	76,35	70,82
7	88,03	80,88	74,78	68,63
8	85,47	77,11	70,18	63,50
9	78,92	69,12	61,39	54,47
10	64,18	52,90	44,98	38,76

Таблица 2. Разрывы смещений для случая нагружения одной трещины

№ эл. Разрыв смещений Dn, мкм № эл. Разрыв смещений Dn, мкм L=2 мм L=2 мм b=0,5 мм b=1 мм b=2 мм b=5 мм b=0,5 мм b=1 мм b=2 мм b=5 мм 1 7,00 6,95 6,93 6,92 11 1,47 0,77 0,34 0,09 2 9,96 9,88 9,85 9,83 12 1,78 0,98 0,46 0,13 3 11,73 11,63 11,58 11,57 13 1,82 1,05 0,50 0,14 4 12,79 12,66 12,61 12,60 14 1,76 1,04 0,52 0,15 5 13,30 13,16 13,10 13,08 15 1,65 1,00 0,51 0,15 6 13,32 13,16 13,10 13,08 16 1,50 0,93 0,48 0,15 7 12,85 12,68 12,62 12,60 17 1,33 0,84 0,44 0,14 8 11,84 11,65 11,59 11,57 18 1,13 0,72 0,39 0,12 9 10,10 9,91 9,85 9,83 19 0,89 0,58 0,31 0,10 10 7,14 6,98 6,93 6,92 20 0,59 0,38 0,21 0,07 № эл. L=5 мм № эл. L=5 мм b=0,5 мм b=1 мм b=0,5 мм b=0,5 мм b=0,5 мм b=1 мм b=2 мм b=5 мм 1 17,82 17,57 17,41 17,32 11 7,20 4,41 2,41 0,86 2 25,39 24,99 24,75 24,61 12 7,90 5,21 3,02 1,14 3 29,95 29,44 29,13 28,96 13 7,67 5,27 3,18 1,26 4 32,73 32,11 31,74 31,53 14 7,14 5,04 3,14 1,29 5 34,14 33,41 32,98 32,75 15 6,50 4,68 2,99 1,27 6 34,33 ,33,49 33,00 32,75 16 5,80 4,24 2,76 1,20 7 33,30 32,35 31,81 31,54 17 5,04 3,73 2,46 1,10 8 30,89 29,82 29,24 28,97 18 4,22 3,16 2,11 0,97 9 26,66 25,49 24,89 24,63 19 3,30 2,49 1,68 0,78 10 19,25 18,08 17,55 17,33 20 2,15 1,63 1,12 0,53 № эл. L=10 мм № эл. L=10 мм b=0,5 мм b=1 мм b=2 мм b=5 мм b=0,5 мм b=1 мм b=2 мм b=5 мм 1 36,33 35,64 35,13 34,75 11 21,49 14,39 8,82 3,84 2 51,85 50,77 49,99 49,40 12 21,90 15,80 10,41 4,90 3 61,31 59,91 58,89 58,13 13 20,48 15,33 10,53 5,23 4 67,18 65,46 64,22 63,32 14 18,66 14,29 10,09 5,22 5 70,32 68,28 66,82 65,78 15 16,72 13,00 9,36 5,00 6 71,05 68,66 66,98 65,82 16 14,75 11,59 8,48 4,64 7 69,37 66,60 64,69 63,41 17 12,71 10,08 7,46 4,18 8 64,99 61,78 59,65 58,27 18 10,58 8,45 6,31 3,60 9 57,03 53,31 50,97 49,57 19 8,23 6,61 4,98 2,88 10 42,69 38,50 36,16 34,92 20 5,34 4,31 3,27 1,92 где l – половина длины трещины, м;

x – продольная координата с началом отсчета в центре трещины, м.

Для получения сравнительных характеристик с известными аналитическими моделями необходимо представить полученные значения разрывов смещений в аналитическом виде

Цх^ш)!^'), где V(x) – вспомогательная функция, определяемая как

4 (1 — у 2 )

v(x) =------p вн ^l2 — x 2(

n

/©

– регрессионное уравнение третьего порядка, определяемое как

f(L) = a0+a 1 l+a2(l) +a3(I)'

где a 0 , a 1 , a 2 , a 3 – неизвестные коэффициенты регрессии.

Используя метод наименьших квадратов (МНК) и полученные значения разры-

вов смещений (табл. 1, 2) были получены значения коэффициентов регрессии для обеих подзадач. Результаты приведены в таблице 3.

Анализируя значения, полученные для условий 1-ой подзадачи можно прийти к выводу о том, что по мере уменьшения величины промежутка b раскрытие трещины приобретает более ассиметричный характер (относительно центра трещины) с увеличением значений у зоны сближения трещин.

Определение коэффициента интенсивности напряжений

В рамках данной статьи КИН первого типа для системы из двух равнонагружен-ных трещин определялся на основе полученных значений разрывов смещений

K i =

ПТ  E       Dn

■ I——---^-lim—=

N32 ⁽ 1 —v ² ) x^l ^l — _x

( 2 )

Таблица 3. Коэффициенты регрессии

Коэффициент регрессии	Подзадача №1	Подзадача №2
a 0	1,2408	1,26688
a 1	0,0982	0,0034
a 2	-0,0036	0,0023
a 3	0,0001	-0,0001

Т.о., преобразовывая (2) подстановкой (3-5) можно получить выражение для коэффициента интенсивности напряжений в зависимости от конфигурации

" ' =^{p H} /^t

L a 0 + a j — + a 2

IS' + a 3 B * )

Анализ полученных результатов

Сравнение полученной численной модели для подзадачи №1 (6) с известными аналитическими моделями (см. (2), (3)) для длины трещины L=5 мм приведено на рисунке 3.

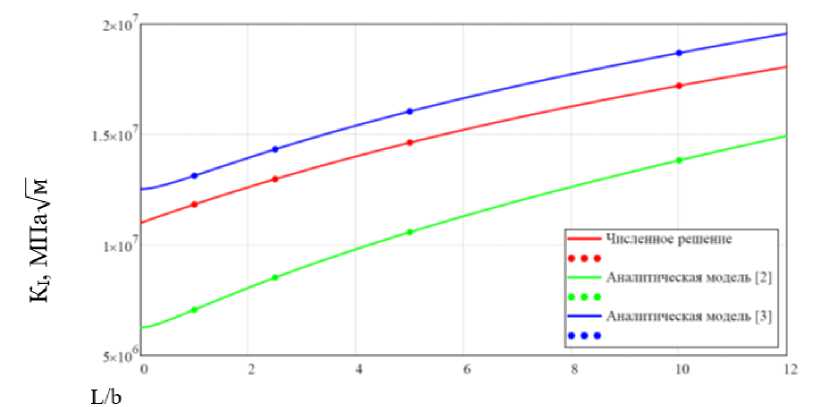
Рис. 3. Сравнение значений КИН

Значения КИН определенные из условий подзадачи №2 приведены на рисунке 4.

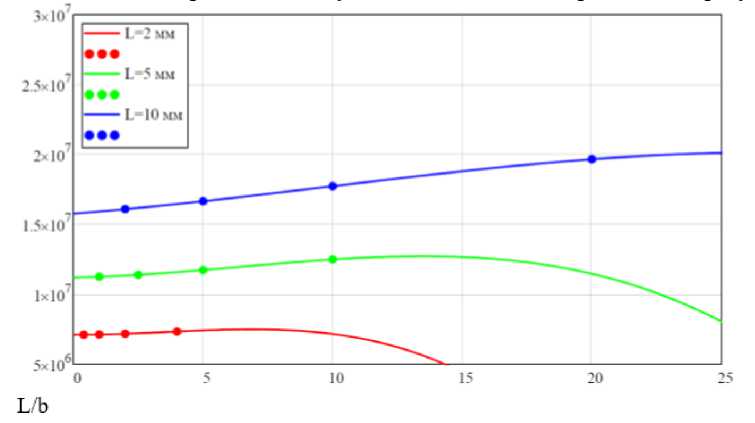
Рис. 4. Значения КИН

Для проведения количественного анализа расхождения полученного численного решения и аналитических решений по полученным расчетным значениям вычисляется относительная погрешность расчета

3 =

1К ан -К чм |

Кан

100% ,

где K ан – значение КИН полученное по моделям [2] и [3];

K чм – значение КИН полученное численным методом по выражению (6).

Результаты расчета относительной погрешности приведены в таблице 4.

Таблица 4. Относительная погрешность расчета (%)

Аналитическое решение	Величина промежутка b , мм
	0,5	1	2	5
[2]	19,6	27,7	34,3	40,3
[3]	8,6	9,7	10,4	11,0